基于ABAQUS 的复合薄膜热结构有限元分析
杨晓丹
(江苏大学 机械工程学院,江苏 镇江212013)
0 引 言
三轴加速度传感器是汽车电子和消费类电子产品市场发展的一个重要方向,有着巨大的市场份额。目前,娱乐系列消费类电子产品(如iPod,iPhone,SonyPS3,Wii 等)都应用了加速度传感器作为动作操控和接收装置。在Wii 和PS3 中,加速度传感器可以灵敏地感测游戏者的动作,并将其转换为游戏中的虚拟人物、物品或交通工具的动作和状态等,并显示在画面中。iPod 和iPhone 中的加速度传感器则可以根据用户的动作而相应地对菜单进行操作。加速度传感器在飞机导航系统中广泛应用,它对GPS 卫星信号实现定位,配合陀螺仪或电子罗盘等元件一起可创建方位推算系统,对GPS 系统实现互补性应用。此外,三轴加速度传感器在硬盘抗冲击防护、子计步器和数码相机的防抖等方面也得到了应用。
本文以热对流[3,4]三轴加速度传感器为研究对象,在已取得的研究成果基础上,针对器件设计和制造中所涉及的关键问题展开研究,重点分析多层复合半导体薄膜悬臂梁在温度场和应力场以及二者的耦合场作用下的形变机制。
1 有限元模型的建立与关键技术的研究
1.1 基本假设
基于有限元基于ABAQUS的半导体硅基复合薄膜弯曲悬臂梁热结构分析是一个复杂过程,因此,对该过程进行数值模拟分析时,有必要做出某些近似和假设。在做热结构分析的过程中,对弯曲悬臂梁挠度变化进行研究时,应做以下两点基本假设[5]:
1)多晶硅腔壁绝热,器件各部分的材料匀质且各向同性;
2)空气与低应力Si3N4和SiO2薄膜的热交换系数为一固定值。
1.2 半导体硅基复合薄膜弯曲悬臂梁模型的建立
半导体硅基复合薄膜弯曲悬臂梁的三维有限元是在ABAQUS/Explicit 软件平台上建立的,有限元模型参数是根据设计实体器件所提供的数据简化而来,有限元模型如图1所示(图中上盖已经被隐藏,这样可以显示内部结构,且垂直于腔体平面向上的为Z 轴正方向)。
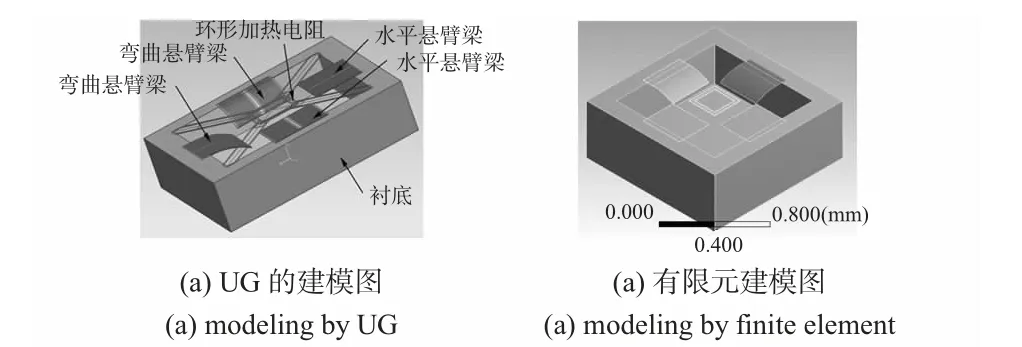
图1 Z 轴测试腔的模型图Fig 1 Model of Z axis test chamber
1.3 材料属性的定义与网格划分及边界条件的定义
腔体材料是多晶硅,用来固定悬臂梁一端和保温绝热,不参与结果讨论,所以,将它定义为刚体。双层悬臂梁的下层是Si3N4[6],杨氏模量E1=226 GPa,密度ρ1=3.44×103kg/m3,泊松比γ1=0.24,与空气的热交换系数h1=0.01 W/(m·K),热膨胀系数α1=2.1×10-6/K,比热C1=0.71 J/(g·K),悬臂梁的上层是SiO2,杨氏模量E2=75 GPa,密度ρ2=2.2×103kg/m3,泊松比γ2=0.17,与空气的热交换系数h2=0.02 W/(m·K),热膨胀系数α2=0.5×10-6/K,比热C2=0.966 J/(g·K),腔体中的填充气体为空气,密度为ρ2=1.29 kg/m3,对流换热系数为h2=0.025 W/(m·K)。
网格划分是通过布置种子来控制网格密度的,种子的近似全局尺寸设置为0.01,网格的单元属性设置为六面体,划分技术为结构化网格划分,设定算法为中性轴算法,有限元模型网格划分如图2 所示。仿真模型中各个部件的接触均定义为无摩擦面接触。
1.4 分析步的定义和载荷定义

图2 有限元模型的网格划分Fig 2 Mesh of finite element model
在实际工作中,水平悬臂梁两端是被固定的,在Z 轴方向上不会发生挠度变形,所以,不作讨论。弯曲悬臂梁的一端被固定在腔壁中,所有方向的自由度被限制住,另一端自由,当弯曲悬臂梁受物理场作用时,需要考虑弯曲悬臂梁的挠度情况。当物理场作用在悬臂梁上时,要在相应的分析步中加载对应的物理量,比如:当有加速度作用在悬臂梁上时,需要在加速度分析步中加载加速度;当温度场作用在悬臂梁上时,需要在温度分析步中加载温度;当加速度和温度场的耦合场一同作用在悬臂梁上时,则需要在加速度分析步和温度分析步中分别加载加速度和温度,便可得到作用在悬臂梁上的耦合物理场。
2 有限元模拟分析
2.1 加速度场对复合薄膜弯曲悬臂梁挠度的影响
2.1.1 Z 轴负方向加速度对弯曲悬臂梁挠度的影响
有限元模拟条件:由于模型中的空气、腔体和加热器不参加计算,所以,新建了一个只有悬臂梁的简易模型,用来加载加速度,模型的尺寸单位为mm。加速度分别取20,40,60,80 gn。方向沿Z 轴负方向,从后处理中得出相对位移的变化,再考虑初始挠度的大小,从而求得弯曲悬臂梁的实际挠度,如图3 所示。

图3 沿Z 轴负方向的加速度对弯曲悬臂梁挠度的影响Fig 3 Influence of acceleration along Z-axis direction on deflection of curved cantilever
从图3 中可以看出:Z 轴负方向的加速度越大,弯曲悬臂梁相对于初始挠度的位移越大,当加速度大小达到80 gn时,弯曲悬臂梁上各点相对于初始挠度的位移变化达到最大,悬臂梁上各点的位移如图4 所示。
由图4 可以看出:当存在80 gn,沿Z 轴负方向的加速度时,弯曲悬臂梁沿Z 轴负方向产生相对位移,位移最大变化量为0.036 7 μm。
2.1.2 Z 轴正方向的加速度对挠度影响

图4 沿Z 轴负方向的加速度为80 gn 时弯曲悬臂梁上各点的相对位移变化Fig 4 Relative displacement change of each point on curved antilever while acceleration is 80 gn along Z-axis negative direction
有限元模拟条件:使用2.1.1 中的简易模型,单位依旧为mm。加速度分别取20,40,60,80 gn,沿Z 轴正方向,从后处理中得出相对位移的变化,再加上初始挠度,求得弯曲悬臂的实际挠度,绘制成曲线图,如图5 所示。

图5 沿Z 轴正方向的加速度对弯曲悬臂梁挠度的影响Fig 5 Influence of acceleration along Z-axis direction on deflection of curved cantilever
从图5 中可以看出:Z 轴正方向的加速度越大,弯曲悬臂梁的挠度变化越小,当加速度大小达到80 gn时,弯曲悬臂梁上各点相对于初始挠度的位移变化达到最大,悬臂梁上各点的位移如图6 所示。

图6 沿Z 轴正方向的加速度为80 gn 时弯曲悬臂梁上各点相对于初始位移的变化Fig 6 Change of each points on curved cantilever relative to initial displacements while acceleration is 80 gn along Z-axis direction
由图6 可以看出:当存在为80 gn,沿Z 轴正方向的加速度时,弯曲悬臂梁沿Z 轴正方向产生相对位移,相对于位移变化量为0.041 0 μm。
2.2 温度场对复合薄膜弯曲悬臂梁挠度影响
有限元模拟条件:由于模型中的空气、腔体和加热器都要参加计算,使用完整的模型,模型的尺寸单位设定为m。(下文的模拟中,都使用这个模型)在实际情况中,由于器件的供电电池所提供的电压是一定的,所以,加热器所达到的相对稳定的温度也是一定的,对加热器加载温度时,只加载360 K 的温度,腔体中会产生一个变化的梯度温度场,温度最终会达到稳定,在腔内温度到达稳定的过程中,弯曲悬臂梁会在Z 轴方向上受热产生形变[7],如图7 所示。

图7 加热器加载温度360K 时弯曲悬臂梁上各点相对于初始位移的变化Fig 7 Change of each points on curved cantilever relative to initial displacements while load temperature of heater is 360K
由图7 可以看出:当加热器温度加载360 K 时,弯曲悬臂梁相对位移的最大变化量为2.721 μm。
2.3 耦合场对复合薄膜弯曲悬臂梁挠度影响
2.3.1 加速度沿Z 轴正方向且加热器恒温保持360 K
有限元模拟条件:加速度分析步中加载加速度分别为20,40,60,80 gn,沿Z 轴负方向。温度分析步中,对加热器加载360 K 的温度,弯曲悬臂梁在耦合场的作用下发生形变[8],从后处理中得出相对位移的变化,再考虑初始挠度的大小,从而求得弯曲悬臂梁的实际挠度,如图8 所示。

图8 360 K 时沿Z 轴负方向的加速度对弯曲悬臂梁挠度的影响Fig 8 Influence of acceleration along Z-axis negative direction on deflection of curved cantilever,at the temperature of 360 K
从图8 中可以看出:沿Z 轴负方向的加速度越大,弯曲悬臂梁的挠度越大,当加速度大小达到80 gn时,弯曲悬臂梁上各点相对于初始挠度的位移变化达到最大,悬臂梁上各点的位移如图9 所示。
由图9 可以看出:加速度为-80 gn,加热器加载温度为360 K 时,弯曲悬臂梁相对位移的最大变化量为2.717 μm。
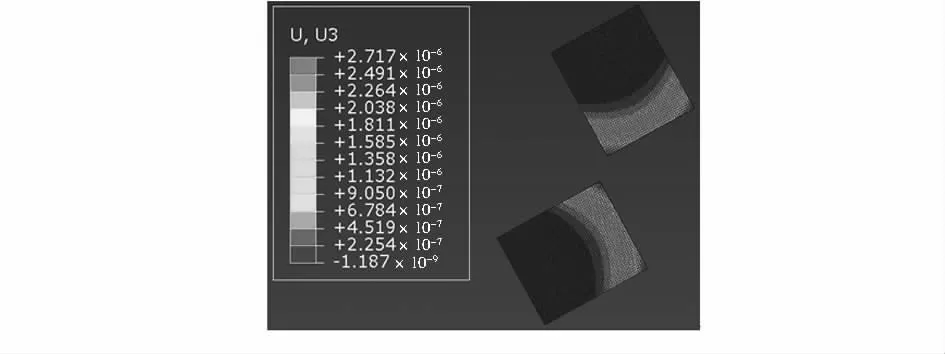
图9 加速度为-120 gn 与加载温度为360 K 时的弯曲悬臂梁上各点相对于初始位移的变化大小Fig 9 Change of relative to initial displacements of each points on curved cantilever while acceleration is-120 gn,load temperature is 360 K
2.3.2 加速度沿Z 轴正方向且加热器恒温保持360 K
有限元模拟条件:加速度分析步中加载加速度,大小分别取20,40,60,80 gn,方向沿Z 轴正方向。温度分析步中,对加热器加载360 K 的温度,弯曲悬臂梁在耦合场的作用下发生形变,从后处理中得出相对位移的变化,再考虑初始挠度的大小,从而求得弯曲悬臂梁的实际挠度,如图10 所示。

图10 360 K 时沿Z 轴正方向的加速度对弯曲悬臂梁挠度的影响Fig 10 Influence of acceleration along Z-axis positive direction on deflection of curved cantilever,at the temperature of 360 K
从图10 中可以看出:Z 轴正方向的加速度越大,弯曲悬臂梁的挠度越小,当加速度大小达到80 gn时,弯曲悬臂梁上各点相对于初始挠度的位移变化达到最大,悬臂梁上各点的位移如图11 所示。

图11 加速度为80 gn 且加载温度为360 K 时的弯曲悬臂梁上各点相对于初始位移的变化大小Fig 11 Changes of each points on curved cantilever relaive to initial displacements while acceleration is 80 gn and load temperature is 360 K
由图11 可以看出:加速度为80 gn,加热器加载温度为360 K 时,弯曲悬臂梁相对位移的最大变化量为2.744 μm。
3 结 论
通过ABAQUS 软件对半导体硅基复合薄膜弯曲悬臂梁在多物理场中的挠度变化进行有限元分析,并对影响挠度变化的因素进行分析比较,可以为器件在实际生产过程中提供一些理论指导和帮助。仿真结果表明:当线性增加沿Z 轴负方向的加速度时,弯曲悬臂梁上的挠度也随之线性增加,最大值为8.596 7 μm;当线性增加沿Z 轴正方向的加速度时,弯曲悬臂梁上的挠度随之线性减小,最小值为8.519 0 μm;当加热器的加载温度为360K,没有加速度作用时,弯曲悬臂梁的挠度变化为5.848 μm;当加热器的加载温度为360 K,沿Z 轴负方向的加速度线性增加时,弯曲悬臂梁的挠度变化也大致呈线性增加,当加速度达到80 gn时,弯曲悬臂梁的挠度为5.843 μm,当加热器的加载温度为360 K,沿Z 轴正方向的加速度线性增加时,弯曲悬臂梁的挠度变化也大致呈线性减少,当加速度达到80 gn时,弯曲悬臂梁的挠度为5.816 μm。通过以上分析,器件Z 轴腔在检测加速度时,弯曲悬臂梁的挠度和加速度之间存在着一定的函数关系,这对于器件的信号检测是十分有利的。
[1] 李 鹏,李昕欣,王跃林.压阻式二氧化硅微悬臂梁化学气体传感器[J].传感器学报,2007(10):1004-1699.
[2] 石亦平,周玉蓉.ABAQUS 实例详解[M].北京:机械工业出版社,2006.
[3] Leman O,Mailly F,Latorre L,et al.Noise analysis of a first-order thermal sigma delta architecture for convective accelerometers[J].Analog Integr Circuits S,2010,63(3):415-423.
[4] Choi J C,Kong S H.Performance analysis of a convection-based tilt sensor[J].Jap J Appli Phys,2010,49(6):06GN15.
[5] 李纯金,杜佐飞.大弯曲半径管材推弯回弹有限元分析[J].机械设计与制造,2013(6):94-97.
[6] 俞 诚.等离子氮化硅应力的研究[J].半导体技术,1996(3):26-28.
[7] 刘双丽.双金属热制动器的设计与仿真[J].中北大学学报,2008(29):554-557.
[8] 郑文涛,徐永超,张士宏.铝合金手机壳的温热液压成型实验及模拟研究[J].塑性工程学报,2006(5):92-95.

