基于光流和惯性导航的小型无人机定位方法*

宋 宇，翁新武，郭昕刚

(长春工业大学 计算机科学与工程学院，吉林 长春130012)

0 引 言

光流的概念是由Gibson 于1950 年首先提出的，是指空间运动的物体在成像面上的像素运动的瞬时速度，它表征了二维图像的灰度变化和场景中物体及其运动的关系［1］，它根据像素灰度的时域变化和相关性确定各个像素点的运动速度，因此，可被观察者用来确定目标的运动情况［2］。对光流的研究成为计算机视觉和有关研究领域中的一个重要部分。因为在计算机视觉中，光流扮演着重要角色，在目标对象分割、识别、跟踪、机器人导航以及形状信息恢复等都有着非常重要的应用［3］。

光流传感器是一种把图像采集系统(image acquisition system，IAS)和数字信号处理器(digital signal processor，DSP)整合到一个芯片上，并内嵌光流算法的一体式视觉传感器。光流传感器能对视觉运动进行测量并输出二维测量值，常用于计算机的光电鼠标中，作为测量鼠标运动的主要感应元件。此外，光流传感器也用于机器人进行视觉运动测量［4］和相对运动感知［5］。近年来，使用光流法进行飞行导航［6］和避障［7］也成为小型无人机研究领域的一个热点问题。

虽然在机器人视觉中已经大量使用光流法进行导航和避障，但是将二维光流信息与六自由度信息融合进行运动估计的方法还不是很成熟。本文将介绍如何把二维光流数据与惯性测量单元(IMU)通过扩展卡尔曼滤波器(EKF)进行数据融合，得到全向的六自由度飞行状态。此外，该算法使用了捷联式惯性导航系统(SINS)方程，而不是专用的平台导航系统方程，本文提出的算法可以用于任何六自由度的平台。

1 光流传感器工作原理与运动检测

1.1 光流传感器工作原理

光流传感器通过IAS 以一定速率连续采集物体表面图像，再由DSP 对所产生的图像数字矩阵进行分析。由于相邻的两幅图像总会存在相同的特征，通过对比这些特征点的位置变化信息，便可以判断出物体表面特征的平均运动，这个分析结果最终被转换为二维的坐标偏移量，并以像素数形式存储在特定的寄存器中，实现对运动物体的检测。

1.2 光流测量

假设光流传感器的坐标系与飞行器机体坐标系对齐，光流传感器的视场角为α(弧度)，视场宽度为d，视场宽度对应的像素总数为Np，飞行器水平运动速度为v，飞行器距离地面高度为H，那么由光流传感器测得的光流经过采样时间Δt 积累得到像素数(nx，ny)，通过光流传感器的参数将像素点转换为弧度形式的角增量(θx，θy)

1.3 运动补偿

假设飞行器位置固定不变，飞行器做横滚或俯仰运动时，关于绕机体坐标系x 或y 轴的任何旋转将表现为光流。因为光流传感器的坐标系与机体坐标系对齐，所以，一个绕x 轴的旋转将得到y 轴的光流变化;反之，亦然。而飞行器绕z 轴旋转时，由于光流围绕着图像中心旋转将被平均，导致光流为零，所以，绕z 轴旋转不用进行补偿。

旋转运动可以通过旋转矢量Φ=［φxφyφz］T及其微分方程［8］来描述

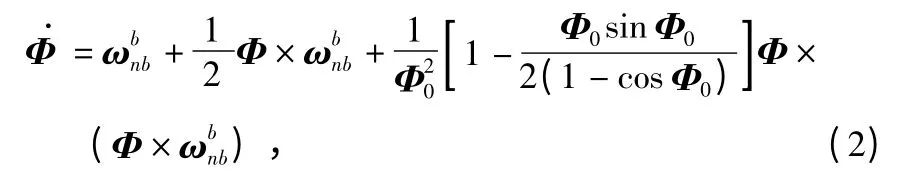
由式(1)和式(2)可以计算得到飞行器横滚和俯仰时所引起的光流误差

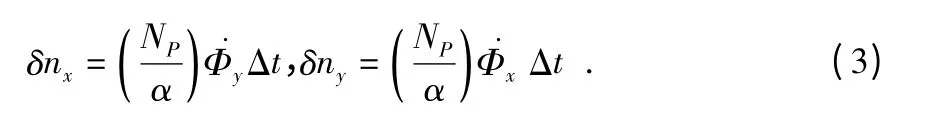
光流传感器实际测量值需要减去该误差值才能得到真正的水平方向运动量。

1.4 地面速度和高度

为了把传感器输出值转换成实际运动的距离，需要考虑高度。如果两个飞行器运动了同样距离，但是一个低，一个高，低的一个会看到表面特征运动得更远，所以，光流数值会更大。假设飞行器运动距离为一固定值，那么，光流的大小和高度呈反比，则光流角增量(θx，θy)也可以表示为

但是只使用一个光流传感器测量时，只能得到速度和高度的比值，而不能分别计算出它们的具体大小。本文采用两个型号一样的光流传感器，分别沿机体坐标系z 轴一高一低安装，两者高度差为L，如图1 所示，则两个光流传感器之间存在下列关系

且有H2=H1+L，经代数运算后得

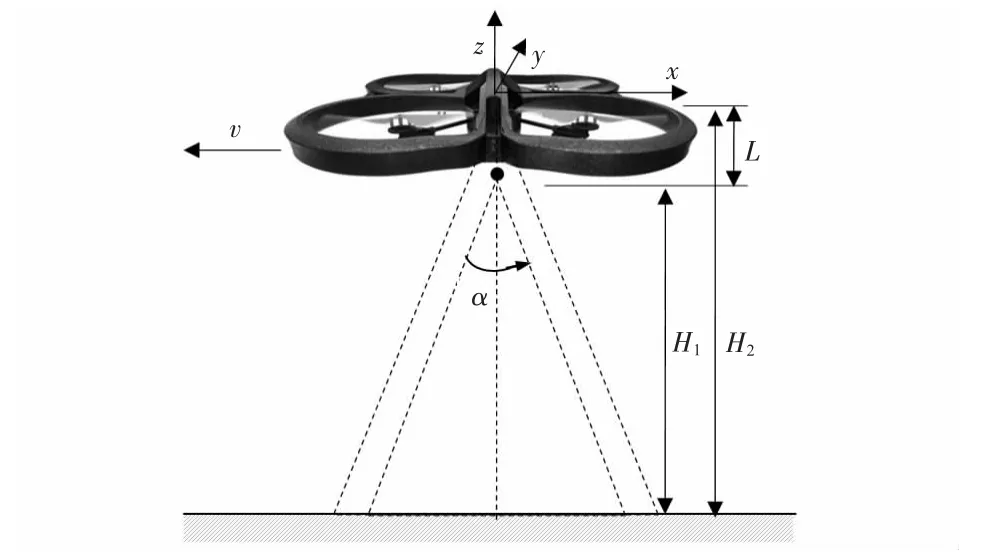
图1 双光流检测几何关系Fig 1 Geometric relationship of dual optical flow detection

2 光流组合导航

2.1 系统模型分析与建立

在概率导航中，关注的是在给定观测值Zk条件下，飞行器状态Xk在k 时刻出现的概率，即为后验概率

由贝叶斯公式可以得到

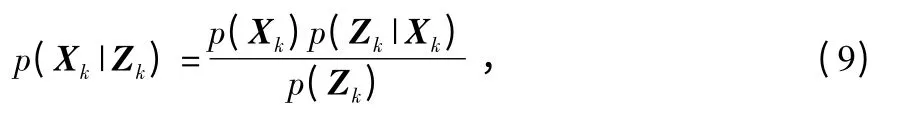
式中 p(Xk)为Xk的先验概率，p(Zk|Xk)为Xk的相似度函数，p(Zk)为Zk的先验概率，也作标准化常量。

根据查普曼—科尔莫戈罗夫(Chapman－Kolmogorov)方程［9］，可以得到该系统预测状态的概率密度函数为

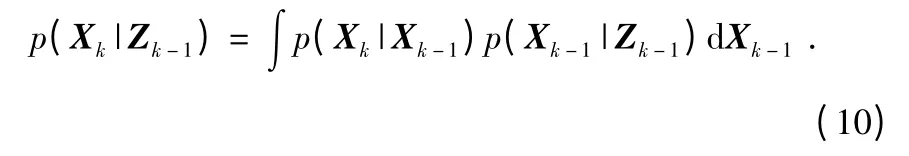
在已知观测值条件下，根据贝叶斯公式，那么后验概率就等于预测状态的概率密度函数和观测似然的乘积，然后再乘以比例系数，得

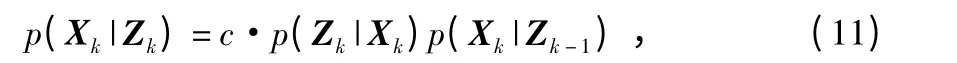
式中 c 为标准化常量的倒数。

在大多数应用中直接使用上述方法是不可行的，这里需要假设条件概率满足高斯分布，这时，可以有效利用EKF进行状态估计。图2 为使用EKF 系统结构示意图，光流传感器测量值首先和惯性测量、高度测量和航向测量的预测值相比较，然后再送入EKF 中，最后得到系统的位置、速度和姿态信息。

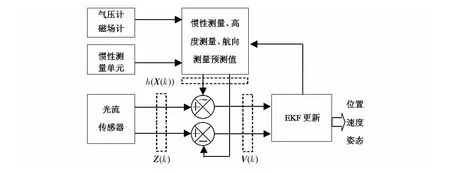
图2 使用EKF 的系统结构图Fig 2 Structure of system using EKF

2.2 状态模型

在应用EKF 时，必须建立系统的状态模型，本文的状态模型实际上是一个非线性惯性导航模型，这里取位置、速度和姿态作为系统的状态量Xk=［P V Ψ］T，则有

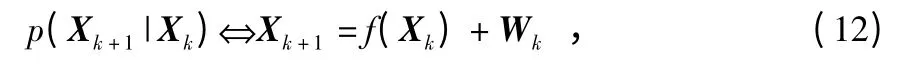
式中 f(·)为非线性状态转换函数，Wk为过程噪声，然而f(·)不能直接应用在协方差中，取而代之的是计算雅可比矩阵，这样系统所传播的不确定性其实就是使用雅可比矩阵和过程噪声强度的近似。

2.3 观测模型

取双光流传感器的测量值Zk=［nx1ny1nx2ny2］T作为系统的观测模型，则有

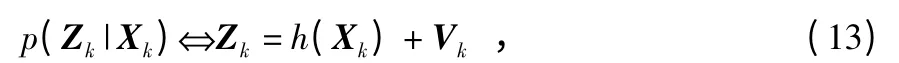
式中 Vk作为观测噪声。通过式(1)、式(3)和式(4)结合可以得到非线性观测模型为

以上各式已经对横滚和俯仰运动进行了补偿。

由于篇幅有限，使用系统状态模型和观测模型进行KF的时间更新和状态更新这里就不在详细描述，具体更新过程可以在文献［10］中找到。

3 实 验

本文采用安捷伦ADNS—3080 光学鼠标芯片作为光流传感器，包含一个IAS、一个DSP 和一个四线串行接口(SPI)，其分辨率为1 600 像素/in(1in≈25.4 mm)，图像采样速率为2 000 帧/s，视场角α 为23°，视场宽度所对应的像素总数NP为30。IMU 采用MPU—6050 模块，包含三轴陀螺仪、加速计和磁场计及气压计，使用I2C 接口直接读取飞行器三个轴的角速率、加速度和磁场大小，以及气压大小。MPU—6050 整合了三轴陀螺仪、三轴加速器，其中角速度测量范围为:±250°/s，±500°/s，±1 000°/s，±2 000°/s，加速度测量范围为:±2，±4，±8，±16 gn，磁场计HMC5583L 的磁场测量范围为 ±(1.3～8)Gs。

本文采用小型四旋翼飞行器作为实验平台，采用两组性能一样的光流模块作为光流传感器，传感器间隔L 为0.1 m，光流传感器的坐标系与飞行器机体坐标系对齐。实验设在室内，为了确保实验中光照强度足够，在房间四周设置4 个500 W 的荧光灯，同时为了使光流传感器采样不失步，本文设置表面纹理分明且平坦地面作为检测面。

实验中，首先通过手动遥控使飞行器达到指定位置，并微调校准各通道使飞行器能够保持当前位置，然后发送指令进入光流传感器辅助的自主悬停，悬停高度为2 m，悬停时间为60 s，主要测试和对比惯性导航和光流辅助导航的定位精度。使用无线数传模块采集各传感器数据，然后通过Matlab 对数据进行处理和显示，得出如下的数据曲线如图3～图5 所示。

从图3～图5 可以看出:当单独使用捷联惯性导航算法时，由于惯性传感器的参数性能较低，即使在开始时经过初始校准，由于惯性传感器误差会随时间而积累，其解算得到的位置、速度和姿态也会随着时间呈现指数发散。而通过EKF 算法将光流传感器与IMU 进行数据融合后，速度和位置误差得到了很好的纠正，光流辅助悬停时x 和y 方向上的最大位置漂移量均小于30 cm，基本满足室内环境下的定位精度要求。

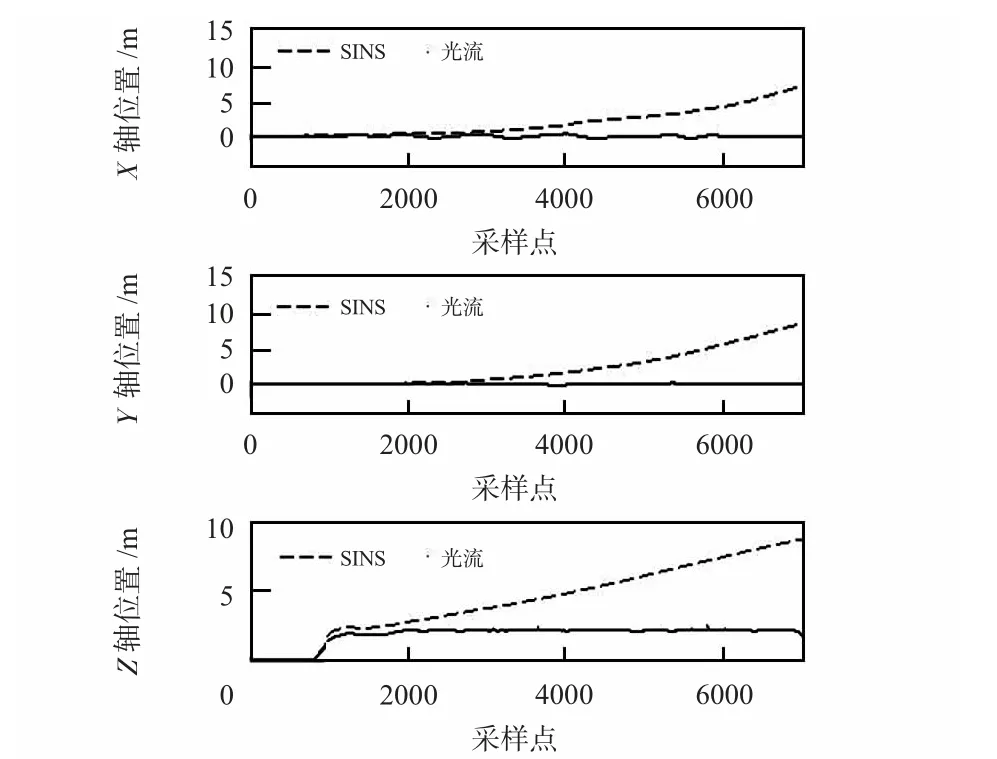
图3 位置比较Fig 3 Position comparison

图6 为在10 m 高度范围内以不同的采样频率得到的像素数之差。可以明显的看出:以10 Hz 采样时(图中实线)需要高度大于3 m 才能分辨出双光流传感器像素数之差，即高度低于3 m 时，就不能得到当前高度。如果想在各高度层都能正常工作，那么，采样速率应当低于1 Hz(图中点划线)。

图4 速度估计Fig 4 Velocity estimation

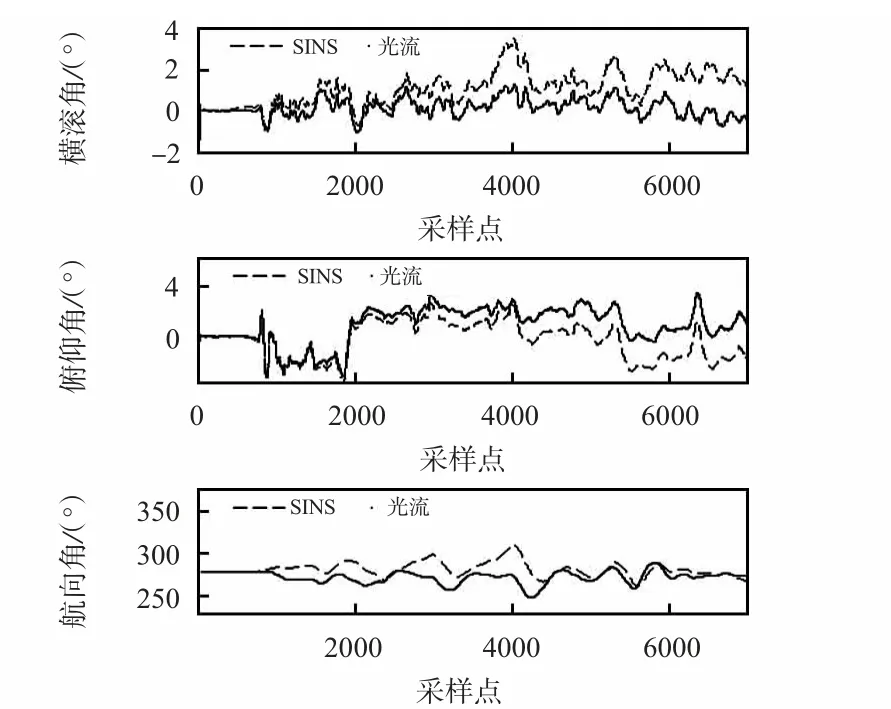
图5 姿态估计Fig 5 Attitude estimation

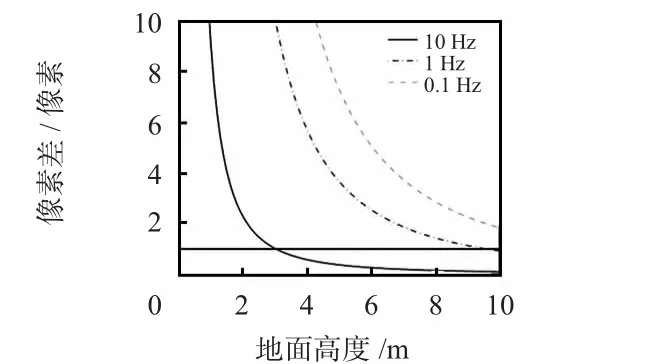
图6 不同采样频率和高度时双光流传感器像素数之差Fig 6 Difference pixel numbers of dual optical-flow sensor with different sampling frequencies and height

4 结 论

本文提出了一种基于光流传感器和IMU 相结合的定位方法，并使用EKF 进行数据融合，得到飞行器的实时位置、速度和姿态信息。实验表明:该方法能够有效提高小型无人机导航性能，减小导航时的位置、速度和姿态误差，可以为小型无人机室内导航提供一种有效的方案。在室外环境时可以通过与卫星导航系统、地形地图等相结合，为小型无人机低空飞行提供更准确的导航。

［1］ 张洪涛，张广玉，李隆球，等.微型二维光流传感器设计［J］.哈尔滨工程大学学报，2014，35(5):619－623.

［2］ Koenderink Jan J.Optic flow［J］.Vision Research，1986，26(1):161－180.

［3］ Sundareswaran V.Egomotion from global flow field data［C］Proceedings of the IEEE Workshop on Visual Motion，Los Alamitos，USA，1991:140－145.

［4］ 于合龙，刘浩洋，苏恒强.基于光流追踪技术的变形位移测量方法［J］.吉林大学学报:理学版，2014，52(2):331－335.

［5］ 郭 力，昂海松，郑祥明.基于单目视觉的微型飞行器移动目标定位方法［J］.系统工程与电子技术，2012，34(5):996－1000.

［6］ Zingg Simon，Scaramuzza Davide，Weiss Stephan，et al.MAV navigation through indoor corridors using optical flow［C］∥IEEE International Conference on Robotics and Automation，Anchorage，USA，2010:3361－3368.

［7］ Green W E，Oh P Y，Sevcik K，et al.Autonomous landing for indoor flying robots using optic flow［C］∥ASME International Mechanical Engineering Congress，2003.

［8］ Bortz J.A new mathematical formulation for strap down inertial navigation［J］.IEEE Transactions on Aerospace and Electronic Systems(AES)，1971，7(1):61－66.

［9］ 现代应用数学手冊编委会.现代应用数学手册/概率统计与随机过程卷［M］.北京:清华大学出版社，2000.

［10］Maybeck P.Stochastic models estimations and control［M］.New York:Academic Press，1982.