基于RBF 神经网络的空间插值法在空气质量监测中的应用*
花晓蕾,唐慧强,2,张红燕,张丽萍
(1.南京信息工程大学 信息与控制学院,江苏 南京210044;2.南京信息工程大学 气象灾害预报预警与评估协同创新中心,江苏 南京210044)
0 引 言
随着人类社会的快速发展,我国生态环境日益恶化,2012 年中国主要城市连续出现空气质量指数突破300 的重度污染,2013 年中国遭遇史上最严重的雾霾天气。据统计,雾霾天涉及25 个省份,100 多个大中型城市,创52 年之最,其频率之高,波及面之广,污染程度之重前所未有,这不仅影响人类日常生活秩序,还严重威胁人类身体健康[1]。因此,实时向公众发布空气质量状况,准确分析大气污染物特征和区域分布趋势,是科学有效的控制区域大气污染的重要手段。
中国监测总站从2000 年6 月5 日开始在各主要城市建设数量不等的空气自动监测站,但这些监测站数量有限,离散、不均匀,仅简单采用监测站点的数据,不能代表整个区域的空气质量。空间插值法[2]根据已知点的信息推测未知地理空间信息,并依据某种函数关系式最好的逼近已知的空间数据,推导出区域范围内其余任意点或分区的值[3],可以很好地满足上述需求。
常用的空间插值法有克里格法、样条曲线法、反比距离加权法等[4],这些插值法现已应用于多个不同的领域[5]。克里格法因估值更加精确而被广泛使用,但其适用条件是区域化变量存在空间相关性,并且假设数据变化服从正态分布,若某些数据存在主导型趋势或不是正态分布,则会降低克里格插值精度[6],因此,这种方法仅限于相对小的空间尺度上。介于克里格法的局限性[7],本文提出基于邻近点输入的RBF 神经网络插值法选择对空气质量监测项目中的PM 2.5,PM 10,CO 和O3进行空间插值,它借鉴了克里格法的插值思想[8],不同的是,它认为地理空间信息具有非平稳性,是空间异质的。空间不确定信息的建模是根据空间分布现象等概率的、可选的数值表达式,定义各种随机变量之间的空间相关,并依据相邻数据将高度不确定的先验分布转化为低不确定性的后验分布,其函数逼近能力强、收敛速度快且需要人为调节的参数少[9],因此,本文提出的RBF神经网络适用于大空间尺度的大气污染物的空间插值预测研究,且实验结果表明此方法用于空气质量的监测表现出较强的优越性。
1 RBF 神经网络结构
RBF 神经网络是以函数逼近理论为基础而构建的一类前向网络[10],本文研究的基于邻近点输入的RBF 神经网络对大气污染物浓度预测模型结构如图1。
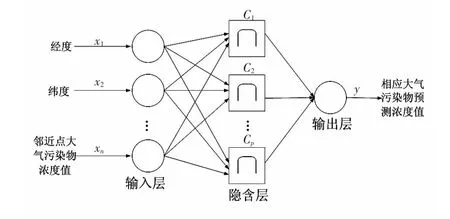
图1 RBF 网络拓扑结构Fig 1 RBF network topology structure
它由三层组成[11],第一层为输入层,本结构的输入层是经纬度坐标和与插值点距离最近的3 个已知监测点的大气污染物浓度值,输入层传递信号到隐含层;第二层为隐含层,节点函数一般选用高斯函数,如公式(1),第三层是输出层,它有一个神经元,即某大气污染物浓度预测值

其中,uj为第j 个隐含层节点的输出,X 为输入样本,Cj为高斯函数中心值,δj为标准化常数,Nh为隐含层节点数。由式(1)可知,节点输出范围为0 和1 之间,且越靠近节点中心的输入样本,输出值越大[12]。
2 神经网络模型构建
2.1 原 理
大气污染物浓度信息插值可以看作是曲面插值问题,即根据已知点数值对所要研究的复杂曲面进行拟合,多种因素综合影响其空间分布规律,考虑到大气污染物污染信息空间分布的复杂性,可以用一个复杂的非线性函数来模拟它们之间的关系,如式(2)

其中,Z 为某大气污染物浓度值,(x,y,A1,A2,…,An)为污染物浓度的影响因素。RBF 网络对该非线性函数逼近:以各站点经纬度[13](即x,y)和与插值点距离最近的n 个已知点的某污染物浓度值(这里n 取3,即A1,A2,A3)为输入,对应的大气污染物浓度值为输出,即网络的输入层节点数为5,其中最后3 个神经元的确定依据空间距离衰减规律:已知点对插值点的影响与它们之间的距离成负相关,因此,网络输入层后3 个神经元为与插值点距离由近至远的已知点的污染物浓度值。网络首先利用训练样本确定网络隐节点的中心和宽度,然后调节网络的连接权值,将输入输出之间的非线性关系隐藏在收敛后的网络之中,最后将未知点的经纬度坐标和与之最近的3 个站点的污染物浓度值作为网络输入,对网络进行仿真预测,即可得到该未知点的大气污染物浓度信息值。
2.2 应 用
2.2.1 实验数据
实验数据来源于南京市环境监测中心站,目前南京市共布设了13 个大气环境监测站点,监测站点的地理空间分布如图2 所示。其中有9 个国控点和4 个郊区点,郊区点为溧水永阳、高淳淳溪、六合雄州和江宁彩虹桥。选取2014 年收集的空气污染物监测项目中的PM 2.5,PM 10,CO 和O3作为区域化变量,以各站点污染物监测日均值为研究基础数据,对南京市各站点的空气质量数据进行空间插值。
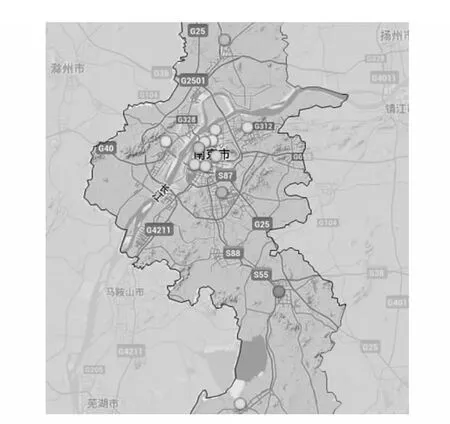
图2 南京市大气环境监测站地理空间分布图Fig 2 Atmospheric environment monitoring station geospatial distribution of Nanjing
2.2.2 模型仿真
模型仿真步骤可总结如下:
1)数据预处理:由于神经网络在进行学习和预测过程中,可能会出现某类数据的绝对值过大,从而偏离神经元的有效区间,使其他分量失去对整个网络的调控能力,为了提高学习速度,首先对原始输入数据进行归一化处理,归一化公式如式(3)所示

式中 Pmax和Pmin为序列中的最大值和最小值。
2)插值点的生成:使用Matlab 的meshgrid()函数在[-1,1]之间生成大量节点的二维网络,每一个节点对应空间中的一组经纬度序列,并采用上述方法进行归一化处理。
3)网络输入生成:以训练样本中各已知站点经纬度坐标为基础,搜索与之最邻近的3 个已知点,按距离由小到大分别赋予输入矩阵的第3,4,5 行,插值点网络输入生成同训练样本网络输入生成。
4)网络训练:选用Matlab 神经网络工具箱提供的newrb()函数建立基函数神经网络,以训练样本数据中的各站点经纬度坐标和最邻近的3 个已知站点大气污染物浓度值对应于网络输入层的5 个节点,相应站点的污染物浓度值作为网络输出,对网络进行训练,网络训练误差设定为0.2,散步常数设置为1.2,经9 步迭代,网络均方差已达到0.087,满足实验要求,如图3 所示。训练获取研究区各大气污染物与5 个输入层节点之间的非线性映射关系,并存储于网络之中。

图3 基于邻近点输入的RBF 神经网络训练图Fig 3 Training diagram of RBF neural network based on neighborhood point inputs
5)网络仿真:将生成的二维坐标矩阵和污染物浓度值代入训练好的RBF 神经网络进行仿真,预测出对应的大气污染物信息值,并反归一化使其重新返回原来的量纲和量级。
2.2.3 实验结果
根据上述步骤,选取迈皋桥国控点半月的大气污染物PM 2.5,PM 10,CO 和O3网络输出结果生成图4 ~图7。

图4 PM 2.5 网络输出结果Fig 4 Result of PM 2.5 network output
从图中可以看出:该模型对样本的拟合效果很好,监测值和预测值偏差不大,说明本文提出的插值方法精度高,预测能力强。

图5 PM 10 网络输出结果Fig 5 Result of PM 10 network output

图6 CO 网络输出结果Fig 6 Result of CO network output

图7 O3 网络输出结果Fig 7 Result of O3 network output
本文同时选用仅基于经纬度输入的RBF 神经网络和基于邻近点输入的RBF 神经网络(记为方案1,方案2)选取迈皋桥站点半月的大气污染物浓度进行预测,表1 是两种方案得出的PM 2.5,PM 10,CO 和O3预测值和监测值的比较。
由表1 可知,对上述四种大气污染物按精度排序为CO >PM 2.5 >PM 10 >O3,虽然基于邻近点输入的RBF 神经网络对大气污染物浓度值的预测仍存在误差,但它们的平均误差和误差均方根均小于方案1,尤其是CO 的预测效果,说明神经网络输入层提供的信息数量对预测的结果有一定的影响,由此表明:本文提出的插值方法对空气质量的预测研究具有良好的适用性。
3 结束语
本文以空间自相关为理论基础,“地理学第一定律”为基本假设:即空间位置上越接近的点具有相似特征值的可能性越大,提出了基于邻近点输入的RBF 神经网络空间插值法,应用于空气质量的监测,此方法具有以下特点:
1)建模方法简便,即只要在研究领域内有一定的监测数据就可以作为RBF 神经网络的训练样本,使网络完成对研究领域内主要大气污染物浓度信息的存贮,并从中发现输入和输出之间的内在规律;
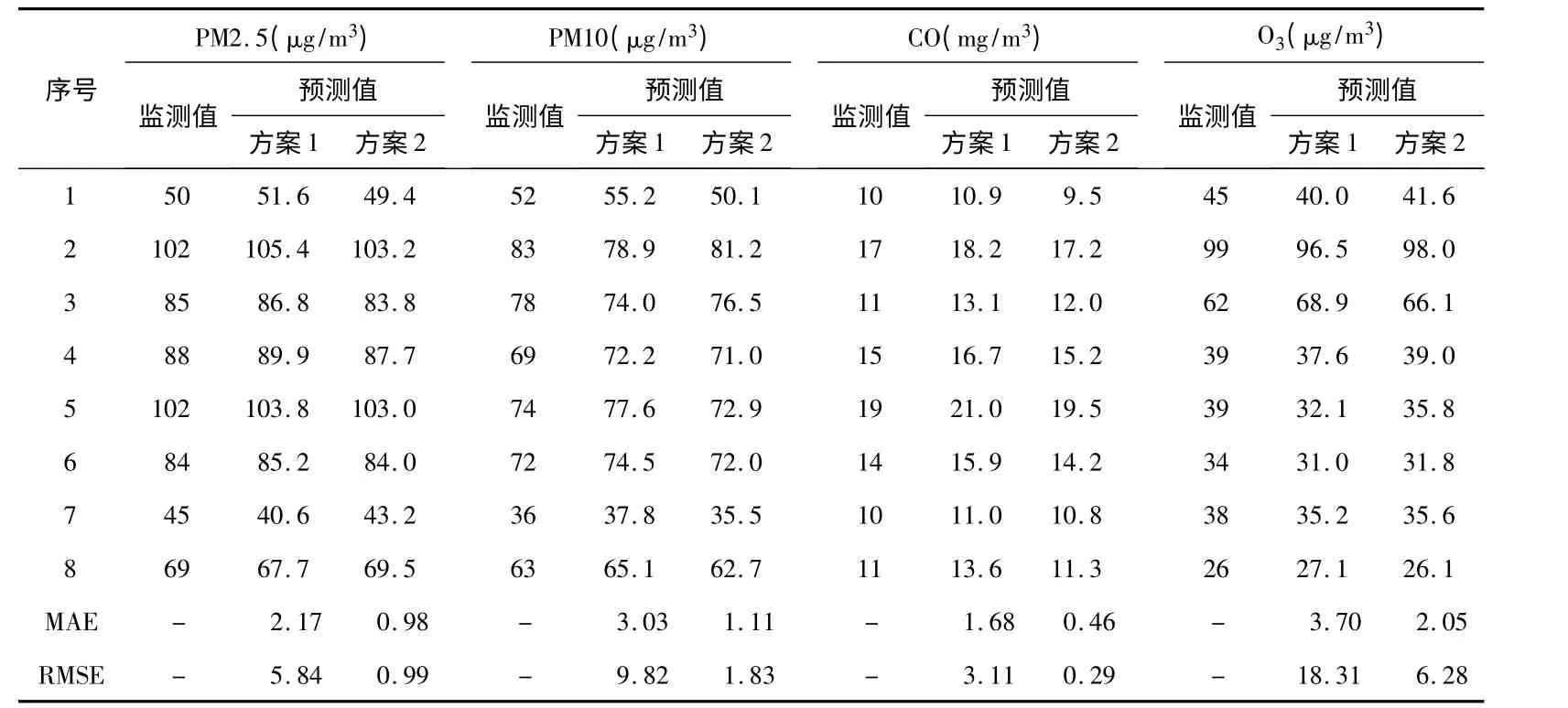
表1 两种方案PM 2.5,PM 10,CO 和O3 预测值和监测值对比Tab 1 Comparison of predictive and monitoring values of PM 2.5,PM 10,CO and O3 of two schemes
2)将RBF 神经网络方法与地理信息系统相结合,充分应用神经网络方法的非线性计算能力和地理信息系统处理地理数据能力,更好地实现对复杂地理系统的定量分析;
3)因大气污染物浓度信息空间分布的复杂性,RBF 神经网络凭借其良好的自学能力和优良的非线性逼近能力高效地解决了此类预测问题,为环保业务提供良好的决策支持;
4)神经网络输入层提供的信息越多,将会提高预测精度,本文采用地理坐标和邻近点作为网络输入,若加入其他因素,如气温、气压、风速等,则有可能得到更准确的插值结果。
[1] 吴 兑,邓雪娇.环境气象学与特种气象预报[M].北京:气象出版社,2001.
[2] 黄杏元.地理信息系统概论[M].北京:高等教育出版社,2001.
[3] 李 新,程国栋,卢 玲.空间内插方法比较[J].地球科学进展,2000,5(3):260-265.
[4] 丁 卉,徐伟嘉,曹生现,等.三种区域空气质量空间插值方法对比研究[C]∥中国环境科学学会学术年会,北京:中国学术期刊电子出版社,2013:7052-7059.
[5] 李军龙,张 剑,张 众,等.气象要素空间插值方法的比较分析[J].草业科学,2006,23(8):6-11.
[6] 李启权.基于RBF 神经网络的土壤属性信息空间插值方法研究[D].雅安:四川农业大学,2006:1-56.
[7] Boznar M,Lesjak M,Mlakar P.A neural network-based method for the short-term predictions of ambient SO2concentrations in highly polluted areas of complex terrain[J].Atmospheric Environment B,1993,27(2):221-230.
[8] 王玉璟.空间插值算法的研究及其在空气质量监测中的应用[D].郑州:河南大学,2010:1-57.
[9] 孟 健,马小明.Kriging 空间分析法及其在城市大气污染中的应用[J].数学的实践与认识,2002,32(2):309-312.
[10]王玉霞.基于RBF 神经网络的PM10 污染预测研究[D].西安:西安建筑科技大学,2008:1-70.
[11]唐慧强,李全月,刘钲江.基于粗糙RBF 神经网络的气象数据插补方法研究[J].计算机工程与计,2014,35(1):282-286.
[12]廖 微,冯小兵,许春冬,等.径向基神经网络的汇率预测模型研究[J].计算机工程与应用,2009,45(24):210-212.
[13]廖永丰,张 莉,王五一,等.城市空气质量GIS 数据模型及分析系统的集成与应用[J].地球信息科学,2007,9(1):123-127.

