基于逆系统方法的强制循环蒸发器非线性控制

刘爱玲，马 欢，齐书康

(1．郑州大学 教务处，河南 郑州450001;2．郑州轻工业学院 软件学院，河南 郑州450001;3．郑州大学电气工程学院，河南 郑州450001)

0 引言

强制循环蒸发器特别适用于蒸发浓稠和带有结晶的溶液，能显著提高生产强度和能量利用效率、改善操作条件，被广泛应用于制药、化工过程、冶金、造纸、食品等生产过程中水相或有机相溶液的蒸发浓缩［1-4］．

强制循环蒸发器是典型的非线性系统，且各个回路间存在强耦合关系［5-7］． 为了提高蒸发器液位恒定、溶液浓度快速跟踪设定目标值，近年来多种非线性控制方法被用到强制循环蒸发器的控制研究．文献［4］采用神经网络和多模型切换方法强制循环蒸发器系统设计了自适应解耦PID 控制器．文献［8］将蒸发器系统模型等效为线性模型和非线性动态模型． 但上述方法均基于系统近似模型研究控制器，难以满足系统大范围控制要求．WANG 等［9］则采用神经网络控制方法对系统设计了自适应切换解耦控制器．UMAR 等［10］研究了强制循环蒸发器的优化控制问题，他们还通过在自优化控制中引入前馈控制提高蒸发器的控制效果［11］，但所提出的控制器设计过程复杂．

状态反馈精确线性化控制方法基于受控系统的非线性动态模型设计控制器，能够保证系统在大范围运行时的动态性能，且设计过程简单．为了同时实现强制循环蒸发器系统的解耦和线性化控制，笔者采用逆系统方法，并结合线性二次型最优控制方法研究强制循环蒸发器的非线性控制问题．

首先分析了强制循环蒸发器系统的结构和工艺流程，并基于物料和能量平衡条件建立了系统的一般非线性动态模型;然后采用逆系统方法分析了系统的右可逆性，并通过将右逆系统串联在受控系统之间构成具有线性传递关系且回路间解耦的伪线性系统;最后，采用最优控制理论设计了线性二次型最优控制器．

1 强制循环蒸发器动态模型

1．1 强制循环蒸发器结构和工艺流程

强制循环蒸发器主要包括分离器和加热器，并依靠强制循环泵实现液体循环，其结构如图1所示，进料口溶液与从分离器流出的部分液体汇合后被强制循环泵压入加热器，与热蒸汽进行热交换．加热后的溶液经加热管进入分离器．分离器中浓缩溶液经出料口排出，部分由分离器下端循环管流出，与进料溶液汇合进行再次蒸发．

1．2 强制循环蒸发器非线性动态模型

由强制循环蒸发器的结构和工艺流程可知热量平衡方程．不失一般性，在强制循环蒸发器动态建模过程中忽略蒸发过程中的少量热量损失，并假设在工作点附近溶液的比热容为常数、蒸汽的汽化潜热为常数．

图1 强制循环蒸发器结构图Fig．1 Configuration of the forced circulation evaporators

首先，根据物料平衡方程可得液位与出料流量、二次蒸汽之间满足的关系如下

式中:A 为分离室截面积;QF为进料流量;QP为出料流量;ρw为水的密度;mv为二次蒸汽流量，满足

式中:ρF为进料密度;cF为进料溶液的比热容;TF为进料溶液的温度;c 为溶液的比热容，假设为常数;ρ 为出料密度;T 为溶液温度;λS为加热蒸汽汽化潜热;λv为二次蒸汽的汽化潜热．

同样地，由物流平衡条件可得出料密度、进料量和二次蒸汽之间满足

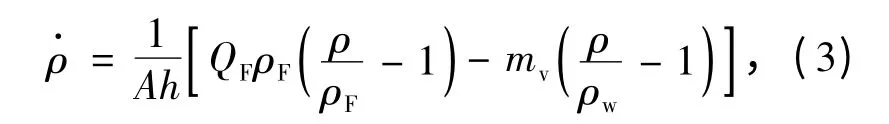
式中:h 为分离室液位高度．

最后，根据热量平衡条件，有

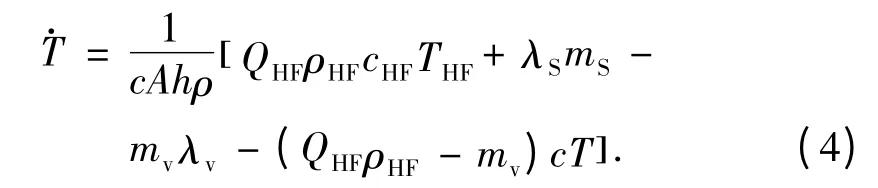
式中:THF为进入加热室溶液的温度;QHF和ρHF分别为进入加热室溶液的流量和密度，满足

式中:QD为循环液体流量．

综合公式(1)～(6)，并选取状态变量x =［x1，x2，x3］T= ［h，ρ，T］T， 输 入 变 量 u =［QP，mS］T，输出变量y =［x1，x2］T，强制循环蒸发器系统可表示为标准非线性系统

2 控制器设计

2．1 基于逆系统方法的强制循环蒸发器反馈线性化

从强制循环蒸发器的动态模型可以看出，该系统具有高度非线性且回路之间存在强耦合． 本小节采用逆系统方法实现系统的精确反馈线性化［12］，同时实现系统回路间的解耦．

首先，对输出y 求导直到u 显式出现

故系统的相对阶r = r1+ r2= 2．根据逆系统理论，强制循环蒸发器系统是α = ［1，1］右可逆的．令φ1=，φ2=，研究中PID 控制器的参数为KP=15，KI=4．仿真结果如图2 ～5 所示．

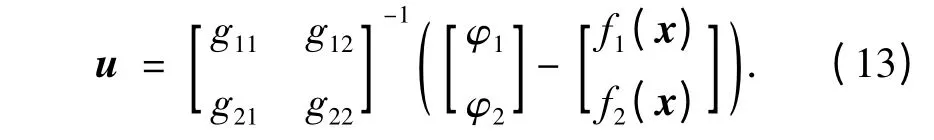
则可得强制循环蒸发器的α 阶积分逆系统，其中φ 为逆系统的输入． 将α 阶积分逆系统串联在强制循环蒸发器系统模型之前，可以实现系统的精确反馈线性化，同时可使得回路间解耦．所得到的伪线性系统可以表示为

图2 液面高度变化曲线Fig．2 Response of the liquid level

2．2 线性二次型最优控制

对上节得到的伪线性系统，利用线性系统控制理论的设计方法可以设计反馈控制器满足需要的动态性能，对伪线性系统设计线性二次型最优控制器．

该伪线性系统的状态空间表达式为

图3 出料密度变化曲线Fig．3 Response of the discharge liquor density

选择性能指标函数

式中:Q = QT≥0，R = RT＞0．

根据线性系统的最优控制理论，可以构造最优控制律如下

φ = －R－1BTPx． (17)

其中矩阵P 是下面Riccati 方程的非负定解

ATP + PA －PBR－1BTP + CTQC = 0． (18)

3 仿真分析

图4 出料流量变化曲线Fig．4 Response of the discharge liquor flow

为了验证所提出的基于逆系统方法的强制循环蒸发器反馈线性化控制(FLC)方案的有效性，将所提控制算法与传统PID 控制器进行仿真比较研究．在仿真中所采用的强制循环蒸发器参数为:QF=80 m3/h;ρF=1 429 kg/m3;λv=2 247 kJ/kg;λS=2 185 kJ/kg;A =40 m2;c =3．61 kJ/(kg·℃)．

在仿真过程中，要求强制循环蒸发器的液面高度保持在2 m，而出料密度的期望值从初始时的1 408 kg/m3变为1 415 kg/m3．此外，在对比仿真

从仿真结果可以看出，与传统的PID 控制方案相比，所提出的基于逆系统方法的精确输入输出反馈线性化控制策略能有效提高液面高度和出料密度控制的准确性，而且响应速度快．此外，从图4 和图5 可以看出，在改变出料密度要求时，能够在大大降低出料流量和加热蒸汽流量的变化量的条件下实现对液面高度和出料密度的精确控制，对实际工业过程具有重要价值．

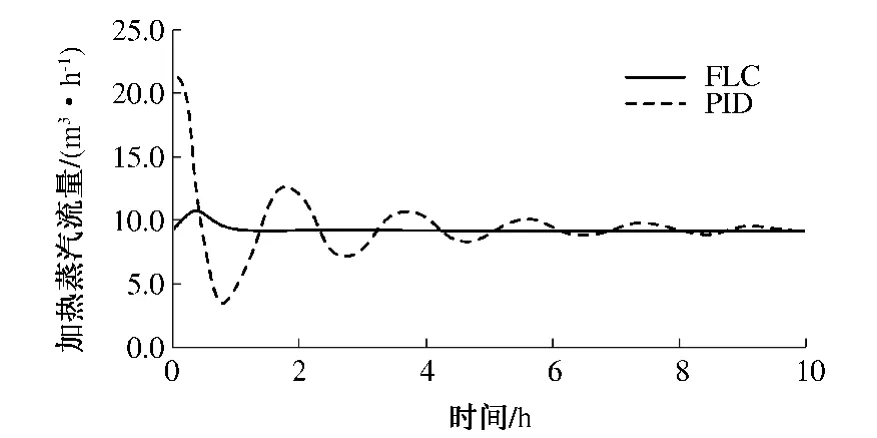
图5 加热蒸汽流量变化曲线Fig．5 Response of the heat steam flow

4 结论

笔者采用逆系统方法研究强制循环蒸发器的非线性控制问题．首先，分析了蒸发器系统的工艺过程并建立了其非线性动态模型;然后采用逆系统方法实现了系统的输入输出精确反馈线性化，同时实现了系统回路间的解耦;最后，对得到的伪线性系统设计了线性二次型最优控制器． 与传统PID 控制的仿真比较，表明笔者所提出的非线性控制器能有效提高蒸发器系统液面高度和出料密度的控制精度，大大降低暂态过渡过程时间，具有重要的实际应用价值．

［1］ 薛允连． 强制循环蒸发器的设计计算［J］． 内蒙古化工，1992，17(1):35 -38．

［2］ 赵军锋，张雨霏，傅毅恺，等． 强制循环蒸发器的设备设计及制造［J］．医药工程设计，2012，33(3):1 -3．

［3］ FARSHAD F，DARIUSH M，JAFARI N M R，et al．Experimental study of forced circulation evaporator in zero discharge desalination process［J］． Desalination，2012，285(1):352 -358．

［4］ 王永刚，柴天佑．强制循环蒸发器系统的非线性自适应解耦PID 控制［J］． 控制理论与应用，2011，28(9):1145 -1153．

［5］ IBRAHIM D，El ABBASS A H，El-EEN F N H． Control of a forced-circulation evaporator system as a case study for control engineering education［C］//Proceedings of the 46th International Midwest Symposium on Circuits and Systems． Cairo:Egypt，2003:1122-1129．

［6］ AGRAWAL S，PATERSON A T，MCLEOD J，et al．Mathematical modelling and analysis of an industrial scale evaporative crystallizer producing lactose monohydrate［J］． Journal of Food Engineering，2015，154:49 -57．

［7］ TUCAKOVIC D R，STEVANOVIC V D，ZIVANOVIC T，et al． Thermal-hydraulic analysis of a steam boiler with rifled evaporating tubes［J］． Applied Thermal Engineering，2007，27(2):509 -519．

［8］ 石宇静，王永刚，柴天佑． 强制循环蒸发系统的多模型预测解耦控制［J］． 系统工程理论与实践，2010，30(1):131 -139．

［9］ WANG Yong-gang，CHAI Tian-you，Fu Jun，et al．Adaptive decoupling switching control of the forced-circulation evaporation system using neural networks［J］．IEEE Transactions on Control Systems Technology，2013，21(3):964 -974．

［10］UMAR L M，XIAO G X，KARIWALA V． Local selfoptimizing control of constrained processes［J］． Journal of Process Control，2012，22(2):488 -493．

［11］ UMAR L M，CAO Y，KAEICALA V． Incorporating feedforward action into self-optimising control policies［J］． Canadian Journal of Chemical Engineering，2014，92(1):90 -96．

［12］李春文，苗原，冯元琨，等． 非线性系统控制的逆系统方法(Ⅱ)—多变量控制理论［J］． 控制与决策，1997，12(6):625 -630，642．