基于混合优化算法的模糊系统辨识

朱晓东，刘 丹，李 广

(郑州大学 电气工程学院，河南 郑州450001)

0 引言

传统模糊系统在面临大量输入变量时会遭遇维数灾问题，从而限制了传统模糊系统的应用．为解决多输入模糊系统“维数灾”问题，1991 年Raju等［1］等提出了一类串联型分层模糊系统，这种分层模糊系统在解决维数灾问题时也带来了其他问题，如分层模糊系统的结构复杂、待辨识参数较多、中间变量无物理含义等．笔者前期提出一种新型分层模糊系统结构形式［2］:后件直联型分层模糊系统(Consequent-Cascade type of hierarchical fuzzy system，CCHFS)，该系统能够避免中间变量所带来的问题，同时不会大量增加辨识参数．对于后件直联型分层模糊系统，在此基础上，笔者又提出一种基于混合优化算法的模糊系统辨识方法，即利用粒子群算法辨识分层模糊模型的前件参数，采用递推最小二乘估计算法(RLSE)辨识结论参数，利用Mackey-Glass 混沌时间序列及Box-Jenkins 数据进行了实验，通过对比其他优化算法，表明该混合优化算法能够提高分层模糊系统模型的逼近精度．

1 后件直联型分层模糊系统

笔者前期研究［2］所提出的后件直联型分层模糊系统如图1 所示，该分层模糊系统结构将中间变量作为模糊单元输出的一个调整项，不但能避免模糊推理过程中对中间变量的处理，而且能够大量减少规则数目和辨识参数数目，同时每层模糊单元只有两个输入量．

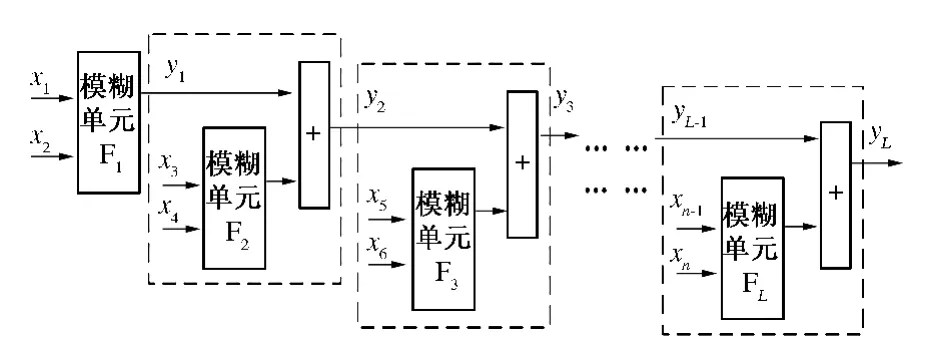
图1 后件直联型分层模糊系统结构Fig．1 The structure of the Consequent-Cascade type of hierarchical fuzzy system

CCHFS 的每一层模糊单元均采用T-S 模糊模型，当模糊系统采用高斯隶属函数、单点模糊化、乘积推理、加权平均解模糊方法时，输入xk=(xk1，xk2)的第k(k = 1，2，…，L)层模糊单元的第i 条规则为:

第k(k=1，2，…，L)层模糊单元的输出为

式中:yk-1(y0=0)为第k -1 层模糊单元的输出;bk(b1=0)是相应输出的系数(xkj)= exp(- 0．5 (xkj-)2/2)为高斯隶属函数(xkj)中相应的参数．

2 后件直联型分层模糊系统辨识

后件直联型分层模糊系统模型的辨识，主要包括输入变量的选取，规则前件参数辨识，模型输出后件参数优化．

2．1 输入变量的选择

输入变量选择是在有限个输入变量中选取对系统输出影响较大的变量，主要方法有:贝叶斯法［3］、偏最小二乘法［4］、PMI 指标法［5］等，笔者采用一种基于最小二乘法［6］的变量选择方法，此方法在保证数据可靠性的基础上，可避免利用模型算法进行变量重要性分析时由于模型选择不当所带来的误差．

2．2 辨识前件参数

粒子群优化算法(Particle Swarm Optimization，PSO)是Kennedy 等提出的一种智能优化算法．该算法占用计算机内存少，不依赖于问题的具体领域，尤其适用于求解一些非线性、多参数复杂系统的全局优化问题．

2．2．1 粒子编码

采用实数编码方式，对于具有L 层模糊单元的后件直联型分层模糊模型，粒子xl(l =1，2，…，M)为该模糊模型的输入变量所对应的高斯隶属度函数(xkj)参数的集合，即xl= (ml，σl);ml=;σl=?;粒子种群数为n;k(k=1，2，…，L)表示第k 层模糊单元;M 为每个输入变量的模糊子集数．

2．2．2 适应度函数设计

适应度函数取分层模糊系统模型输出与实际输出值的均方根误差(RMSE)，即

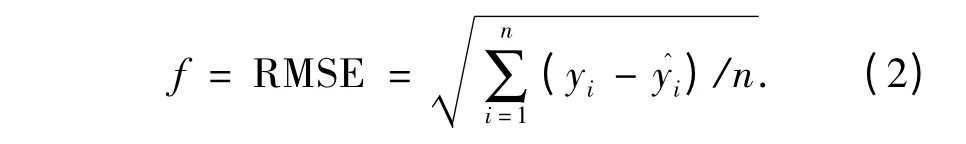
式中:yi为待辨识对象的实际输出为分层模糊系统模型的输出．

2．2．3 速度、位移的更新策略

粒子的速度、位移更新策略决定了算法的收敛速度和精度，更新策略如下

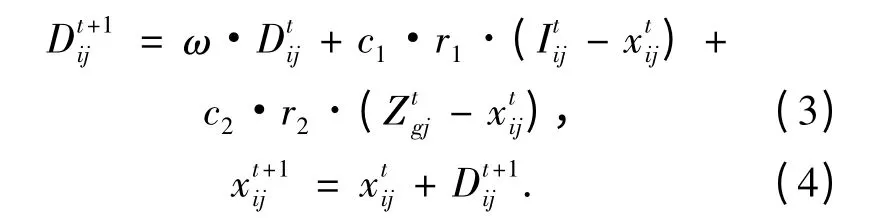
2．2．4 算法步骤

1)初始化参数，并随机产生种群的位置和速度;

2)按照式(2)计算初始种群中个体的适应值;

3)更新每个粒子的个体最好位置:

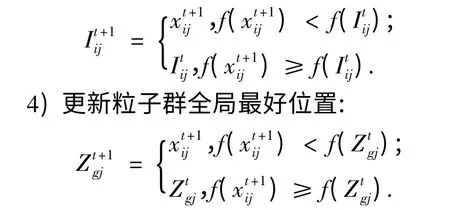
5)根据式(3)、式(4)调整所有粒子的移动速度及其位置;

6)重复执行步骤2)～5)，直至达到最优解对应的适应度函数值保持不变，或者迭代次数已达到设定的最大值，则算法终止．

2．3 后件参数的辨识

后件参数的辨识采用递推最小二乘法，针对上述的后件直联型分层模糊系统，定义

则式(1)可以写为

一个具有L 层模糊单元的分层模糊系统，设有n 组输入输出数据，则第k 层模糊单元的输入输出数据为，yki)，式中=，则可得到:

式中:ykq(q=1，2，…，n，y0q=0)表示第k 层模糊单元的第q 组输出;P 为L = (3NK+1)维的列向量，P 的最小二乘估计为P*= (XTX)-1XTY．为了迭代优化结论参数向量P 及避免矩阵求逆，采用递推最小二乘算法，公式为

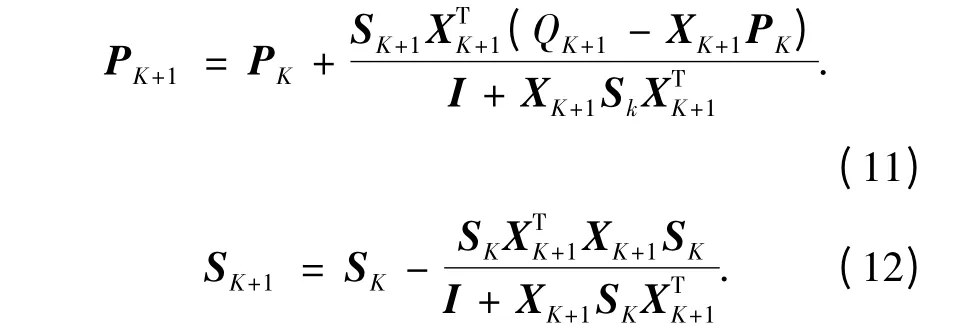
式中:XK+1(K=0，1，2，…，n-1)表示式(10)中X 的第k 个行向量;QK+1表示式(8)中Y 的第k 个元素;P 是结论参数向量，P0=0;S 是增益矩阵，S0= CI，C 一般取大于104的实数，I 为L 维的单位矩阵．

3 辨识算法

综上所述，对具有L 层模糊单元的后件直联型分层模糊系统，其完整辨识算法如下:

(1)对分层模糊系统模型，采用基于最小二乘的变量选择方法分配每层模糊单元的输入量;(2)选定隶属度函数的形状，设置输入变量的模糊空间划分个数;(3)以期望输出为参照，利用粒子群算法优化模型的前件参数，在此基础上利用递推最小二乘依次计算每一层模糊单元的后件参数;(4)由前一步所得到的分层模糊模型计算模型输出，重复第三步进行迭代优化，直至达到结束条件．

4 仿真

以Mackey-Glass 混沌时间序列及Box-Jenkins煤气数据为仿真对象，验证建立后件直联型分层模糊模型，利用笔者所提混合优化算法，进行模型辨识，同时，将杂草优化算法以及果蝇优化算法作为比较，在这两种方法中，所有输入变量模糊子集的隶属函数均采用高斯隶属函数，且后件参数的辨识均采用递推最小二乘法．

方法1 中，采用果蝇优化算法［8］优化前件参数，初始化果蝇种群位置X0，Y0，寻找食物方向X=X0+rand(b，2dc);Y=Y0+rand(b，2dc)，其中，b为种群规模;d 为模糊系统所有输入变量的个数．

方法2 中，采用入侵杂草优化算法［9］优化前件参数，初始种群中目标函数为r 的杂草产生新种子个数N = (r-r0)(s1-s0)/(r1-r0)+s0，其中，s0，s1分别为最小、最大种子数目;r 的变化范围为［r0，r1］．第t 次迭代的标准差σt=(t1-t)n(σ0-σ1)/t1+σ1，当前迭代次数t 变化范围为［t0，t1］;σ0，σ1分别为起始、最终标准差;非线性调和指数n 取为3．

4．1 Mackey-Glass 混沌时间序列建模与预测

将笔者提出的建模方法用于Mackey-Glass 混沌时间序列建模与预测，该时间序列可表示为

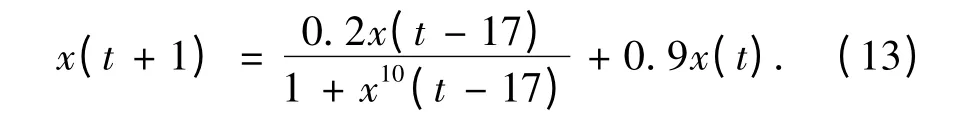
x(0)～x(17)赋初值1．2，选取1 000 组数据，即t = 124，125，…，1 123．采用最小二乘法确定输入变量x(i)对输出变量的影响imp(x(i))，结果如表1 所示．

表1 输入变量的重要性排序Tab．1 The importance ranking of the input variables

利用笔者提出的方法，采用表2(所有模型的输出变量均取为x(t+1))中的4 个输入变量的后件直联型分层模糊系统模型，输入变量均取3 个模糊子集，将前500 对当作训练数据，其余500 对作为测试数据以验证模糊模型的有效性，对混沌时间序列进行建模与预测．取误差e=f*-y，f*为模糊模型的输出，y 为混沌时间序列的实际输出，图2 给出了检验数据的仿真实验结果．

仿真结果表明，笔者提出的辨识方法辨识精度较其他两种的精度高．

4．2 Box-Jenkins 煤气炉数据建模与预测

选用著名的Box-Jenkins 煤气炉数据来辨识燃烧炉的分层模糊系统模型，输入数据u(t)是甲烷的流量，输出数据y(t)是CO2含量的百分比．取t = 5 ～296，即292 组数据，将u(t)与y(t)的历史值作为输入变量x(i)，计算输入变量x(i)对输出变量y(t)的影响imp(x(i))，结果如表3所示．

根据笔者所述的辨识算法，采用表4(所有模型的输出变量均取y(t))中有3 个模糊单元的后件直联型分层模糊系统模型，且变量均取3 个模糊子集，仿真结果如图3 所示．

实验结果表明，笔者提出的基于混合优化算法的辨识精度要高于其他两种算法，是一种较为有效的模糊模型辨识方法．

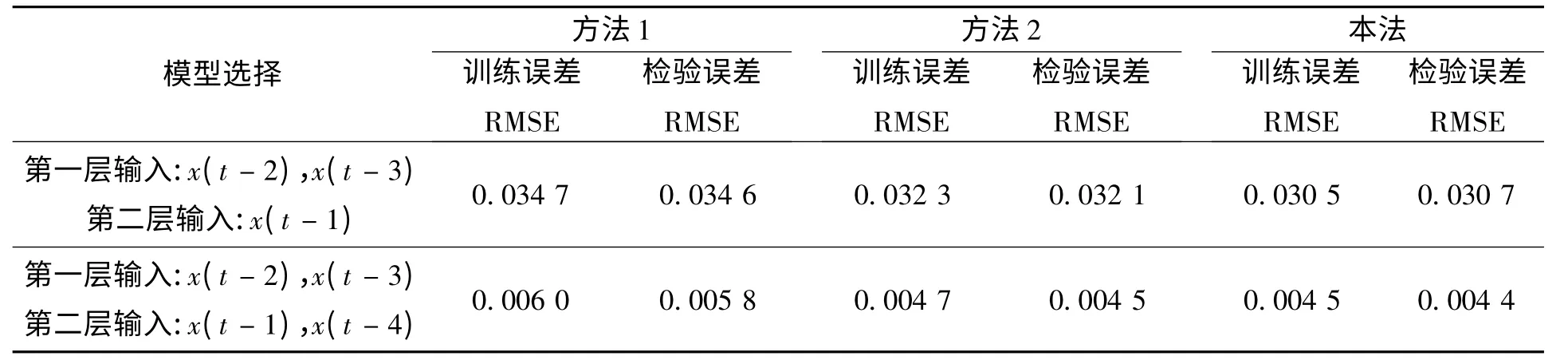
表2 3 种模糊辨识方法比较(M-G 混沌数据)Tab．2 Comparison of three kinds of fuzzy identification methods (M-G chaos data)

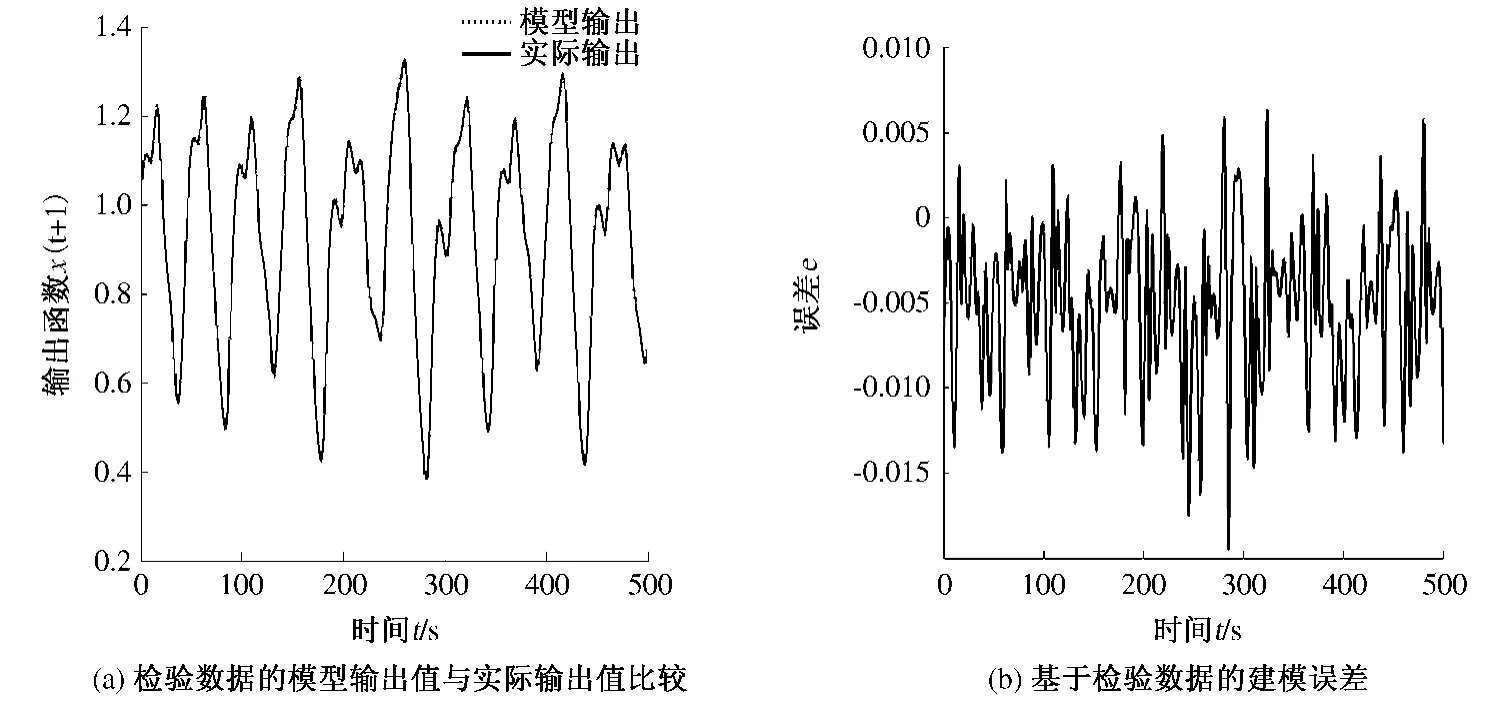
图2 仿真实验结果Fig．2 The simulation results

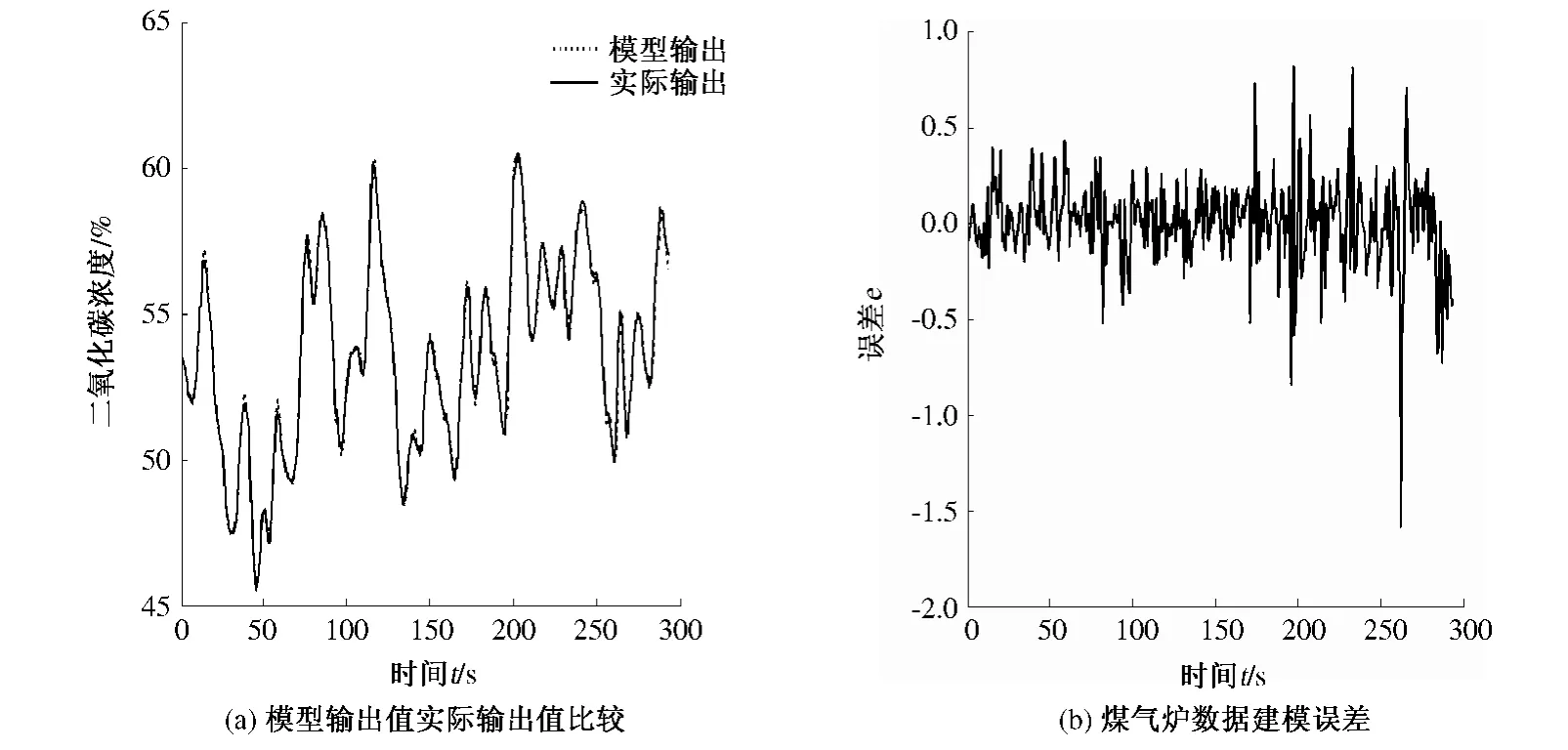
图3 仿真实验结果Fig．3 The simulation results

表3 输入变量的重要性排序Tab．3 The importance ranking of the input variables

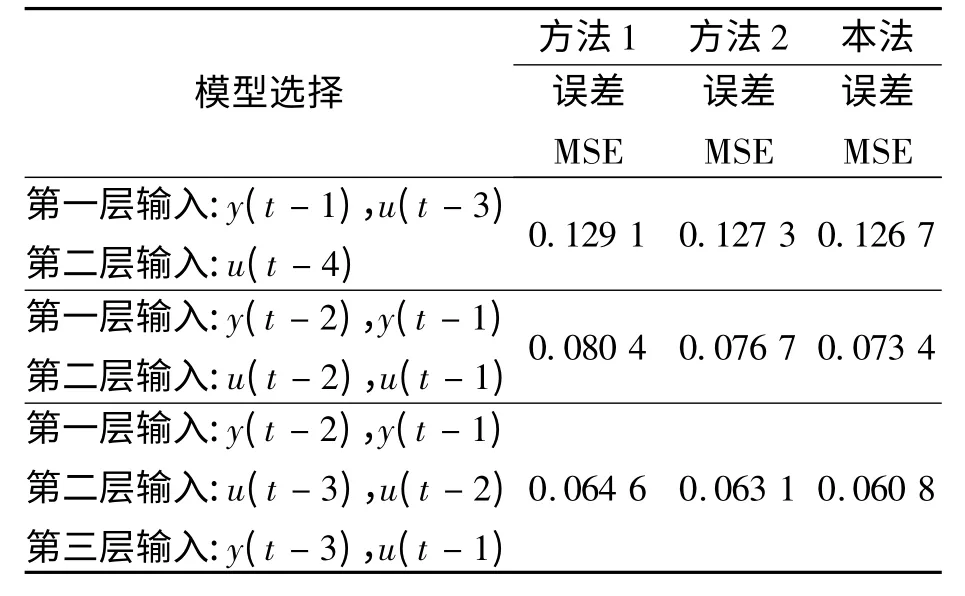
表4 3 种模糊辨识方法比较(Box-Jenkins 数据)Tab． 4 Comparison of three kinds of fuzzy identification methods (Box-Jenkins data)

5 结论

笔者针对一种新型结构的分层模糊系统，提出了一种混合优化算法进行模型优化，并将该混合优化算法与果蝇优化算法、入侵杂草优化算法分别对Mackey-Glass 混沌时间序列及Box-Jenkins数据进行仿真实验，实验结果表明，笔者所提出的混合优化算法能够获得较高的逼近精度，是一种有效的辨识优化算法．

［1］ RAJU G V S，ZHOU Jun，KISNER R A． Hierarchical fuzzy control［J］． International Journal of Control，1991，54(5):1201 -1216．

［2］ 朱晓东，王杰． 一种新型分层模糊系统及其逼近性能［J］． 控制与决策，2013，28(10):1559 -1563，1567．

［3］ O'HARA R B，SILLANP M J． A review of Bayesian variable selection methods:what，how and which［J］．Bayesian Analysis，2009，4(1):85 -117．

［4］ MEHMOOD T，LILAND K H，SNIPEN L，et al． A review of variable selection methods in partial least squares regression［J］． Chemometrics and Intelligent Laboratory Systems，2012，118:62 -69．

［5］ GRADISAR D，GLAVAN M． Input variable selection algorithms for HPC［C］∥Proceedings of 2012 IEEE International Conference on Industrial Technology (ICIT)． Athens:IEEE Service Center，2012:66 -71．

［6］ CHUNG Fu-lai，DUAN Ji-cheng． On multistage fuzzy neural network modeling［J］． IEEE Transactions on Fuzzy Systems，2000，8(2):125 -142．

［7］ 徐龙琴，刘双印． 基于PSO-WSVR 的短期水质预测模型研究［J］． 郑州大学学报:工学版，2013，34(3):112 -116．

［8］ 刘成忠，黄高宝，张仁陟，等． 局部深度搜索的混合果蝇优化算法［J］． 计算机应用，2014，34(4):1060 -1064．

［9］ 左旭坤，苏守宝． 多子群入侵杂草优化算法研究及应用［J］． 计算机工程，2014，40(2):184 -188．