基于模型参考自适应的网络控制系统随机时延补偿

李健勇，赵 峰，丁青青

(1．郑州轻工业学院 计算机与通信工程学院，河南 郑州450001;2．郑州大学 电气工程学院，河南 郑州450001;3．清华大学 电机与应用电子技术系，北京100084)

0 引言

网络控制系统采用计算机网络作为通信介质，为系统的设计和维护带来了很大便利，但网络时延的存在也对控制系统的动态性能造成很大影响，甚至使得系统不稳定［1-2］．网络时延补偿控制问题已成为网络控制系统研究中的重要内容．

根据网络控制系统中网络通信状态和所采用的网络协议等的不同，网络时延具有不变、随机、相关或者独立等不同特性［3-5］，其中随机网络时延补偿是网络控制系统研究中的重点和难点． 目前在网络时延补偿控制研究中所采用的方法主要有:①通过在网络传输节点中增加数据缓冲区把随机非线性网络时延系统转化为定时延系统并采用现代控制方法进行补偿［6-10］． 该方法简单易用，将不同的网络时延转化为最大时延，降低了系统的实时性，且保守性较强．②根据网络时延的不同特性建立其动态模型，基于随机控制理论进行时延补偿和反馈控制［11-16］．该方法适用于网络时延较小且特性已知的系统，当网络控制系统中随机时延变化较大或分布情况未知时难以取得良好的控制效果．③通过对网络时延进行预估并进行在线补偿．由于Smith 预估器对纯滞后系统具有良好的补偿效果，近年来被应用于随机网络时延补偿控制研究［17］．改进的Smith 预估控制方法不依赖于时延特性．但当系统中存在外部干扰时，难以实现Smith 预估模型与实际模型的匹配，影响了系统的动态性能．

针对上述时延补偿控制研究中存在的问题，笔者提出一种基于模型参考自适应控制(Model Reference Adaptive Control，MRAC)的双端Smith预估随机网络时延补偿控制方案，将Smith 预估模型视为参考模型，把存在外部干扰的实际网络系统模型作为对象模型，设计模型参考自适应控制器使Smith 预估模型和真实模型相互匹配，从而实现对时延的完全补偿．

1 双端Smith 预估补偿控制

本节提出一种具有自适应调节机构的双端Smith 预估网络时延补偿控制系统，在系统中引入模型参考自适应结构的目的是当网络控制系统受到外部干扰时，通过设计自适应控制器实现Smith预估模型与实际系统模型之间的匹配． 该网络时延补偿控制系统的结构如图1 所示，其中:τca和τsc分别为控制器到执行器的传输时延以及传感器到控制器的传输时延;Gp(s)为被控对象的传递函数;C(s)为系统控制器;Gm(s)为Smith 预估模型;D(s)为系统受到的外部干扰;k(t)为可调增益，可通过MRAC 控制器进行调节．

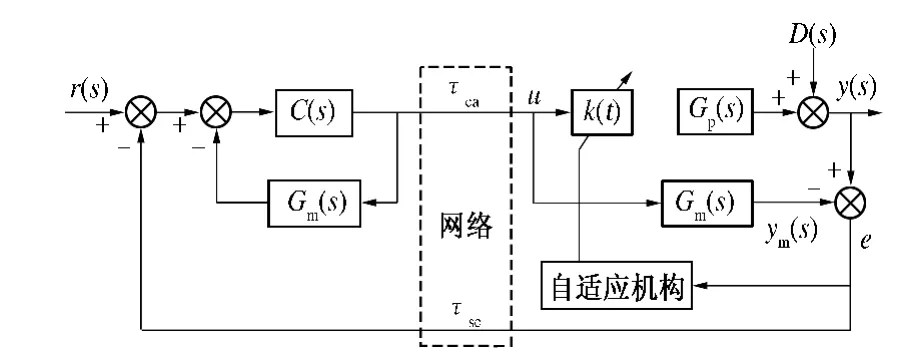
图1 具有MRAC 的双端Smith 预估时延补偿控制系统Fig．1 Configuration of the delay compensation system based on dual Smith predictor and MRAC

闭环系统的传递函数为

为了消除时延τca和τsc对网络控制系统动态性能的影响，需要设计时延补偿系统满足

k(t)Gp(s)+D(s)-Gm(s)=0． (3)

设计Smith 预估器的预估模型

Gm(s)=Gp(s)． (4)

则式(3)可化为

k(t)Gp(s)+D(s)-Gp(s)=0．

即

k(t)Gp(s)+D(s)=Gp(s)． (5)

当系统中不存在外部干扰，即D(s)=0 时，只须令k(t)=1 即可实现网络时延对系统动态性能的影响．但是系统中存在外部干扰时，需要动态地调整k(t)使得式(5)成立．此时闭环系统传递函数和特征方程分别为:

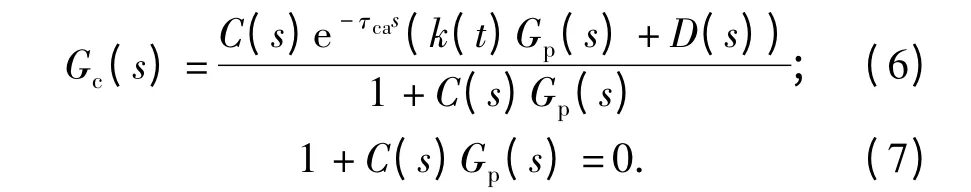
比较式(7)和式(2)可知，当系统中存在外部扰动时，通过动态调节k(t)，可以消除闭环特征方程中影响系统稳定的网络时延的指数项，提高系统的动态性能．

2 模型参考自适应控制器设计

由上节可知在系统存在外部干扰时需要实时地调整k(t)使式(5)成立，从而解决由于时延补偿系统中外部干扰引起的模型不匹配问题． 下面采用模型参考自适应控制方法设计k(t)的动态调整律．

注意到Smith 预估器参考模型为Gm(s)=Gp(s)，而实际系统模型为Gp(s)+D(s)，故预估模型与实际模型输出量的误差e 为

e=ym(s)-y(s)=

uGm(t)-uk(t)Gp(t)-D(t)． (8)

下面设计自适应控制器动态地调整k(t)使得误差趋于0．首先，引入性能指标函数

其中，J 是可调增益k 的函数．为了使指标函数取得最小值，沿着J 负梯度方向调节参数k(t)，使其满足

式中:γ 为可调参数．

为了提高MRAC 的通用性，对模型参考自适应控制算法进行归一化处理，同时引入调节因子a(a ＞0)，以避免在控制器实现过程中出现零除现象:

最后，为了防止在参数调整律过大而造成系统震荡，对调整律的幅值进行限制，保证其在一定的范围之内

式中:β ＞0 为调整律饱和值，满足

结合式(8)、(10)和(12)，可得到基于MARC的可调增益自适应控制律

3 仿真

为了验证笔者所提出的网络时延补偿控制策略的有效性，基于MATLAB 仿真平台中Truetime工具箱对笔者所提控制方案与双端Smith 预估时延补偿控制进行仿真比较研究． 仿真中选取的被控对象模型为

输入信号为方波信号，周期为5 s，占空比为50%，幅值为1．通信类型为CDMA/CD，网络系统各节点无需时钟同步，控制器和执行器为事件驱动，传感器为时间驱动．假设数据传输过程中存在随机时延，数据丢包率为5%．在5 s 时加入功率为0．1 dBW 的白噪声干扰．在两种情况下对系统进行仿真．

Case Ⅰ:Smith 预估模型与系统模型精确匹配，仿真结果如图2 和图3 所示;

Case Ⅱ:Smith 预估模型与实际模型存在偏差，Gp(s)中的参数逐渐变为T1= 1． 5 s，T2=3．6 s，仿真结果如图4 和图5 所示．

图2 双端Smith 预估时延补偿结果(Case Ⅰ)Fig．2 The delay compensation result based on dual Smith predictor (Case Ⅰ)

图3 基于MRAC 双端Smith 预估时延补偿效果(Case Ⅰ)Fig．3 The delay compensation result based on dual Smith predictor and MRAC(Case Ⅰ)

从仿真结果可以看出，在系统存在随机网络时延、数据丢包以及白噪声干扰时，基于双端Smith 预估时延补偿难以取得良好的控制效果，原因在于Smith 预估模型不能与实际系统模型精确匹配，造成闭环系统动态性能降低．而从图3 和图5 基于MRAC 的双端Smith 预估时延补偿控制系统的输出可以看出，在各种情况下采用该控制器闭环系统均具有良好的控制效果，表明该时延补偿控制方案在网络控制系统存在时延、丢包以及外部干扰时均能取得良好的控制效果．

图4 双端Smith 预估时延补偿结果(Case Ⅱ)Fig．4 The delay compensation result based on dual Smith predictor (Case Ⅱ)

图5 基于MRAC 双端Smith 预估时延补偿效果(Case Ⅱ)Fig．5 The delay compensation result based on dual Smith predictor and MRAC(Case Ⅱ)

4 结论

笔者针对网络控制系统中存在的随机时延问题，首先对双端Smith 预估器的时延补偿特性进行了分析，然后设计了基于MRAC 的双端Smith预估器时延补偿控制策略，实现Smith 预估模型与实际系统模型的精确匹配．仿真结果表明:基于MRAC 的双端Smith 预估器能够对网络控制系统存在随机时延、丢包和外部干扰的情况下进行良好的补偿，且在补偿过程中不需要进行时延预测，有效降低了控制系统的结构复杂性，具有重要的应用价值．

［1］ 刘磊明，童朝南，袁立． 关于网络控制系统中的延迟对系统性能影响的研究［J］． 信息与控制，2005，34(3):263 -268．

［2］ 张俊，刘克，薛燕． 基于时延预估的网络控制系统研究［J］． 控制工程，2007，14(1):82 -84．

［3］ 杨丽曼，李运华，袁海斌． 网络控制系统的时延分析及数据传输技术研究［J］． 控制与决策，2004，19(4):361 -366．

［4］ DAI Shi-lu，LIN Hai，GE S S． Scheduling-and-control codesign for a collection of networked control systems with uncertain delays［J］． IEEE Trasactions on Control Systems Technology，2010，18(1):66 -78．

［5］ LIAN Feng-li，MOYNE J R，TILBURY D M． Performance evaluation of control networks:Ethernet，ControlNet，and DeviceNet［J］． IEEE Control Systems，2001，21(1):66 -83．

［6］ LUCK R，RAY A． Experimental verification of a delay compensation algorithm for integrated communication and control systems［J］． International Journal of Control，1994，59(6):1357 -1372．

［7］ 于之训，蒋平． 具有传输延迟的网络控制系统中状态观测器的设计［J］． 信息与控制，2000，29(2):125 -130．

［8］ 郑英，胡修林，方华京，等． 基于观测器的网络化控制系统故障诊断方法［J］．系统工程与电子技术，2005，27(6):1069 -1072．

［9］ 熊远生，俞立，徐建明． 网络控制系统的滑模变结构预估控制器的设计［J］． 电气传动自动化，2003，25(4):39 -40．

［10］穆效江，陈阳舟． 滑模变结构控制理论研究综述［J］． 控制工程，2007，14(1):1 -5．

［11］ RICHARD J P． Time-delay systems:an overview of some recent advances and open problems［J］． Automatica，2003，39(10):1667 -1694．

［12］ DING Shi-yun，CHEN Qing-lin． Prediction and compensation of random delay in NCS via improved Smith predictor based on normalized weighted average method［C］//Proceedings of 33rd Chinese Control Conference． Nanjing:IEEE Press，2014:5885 -5889．

［13］刘磊明，童朝南，武延坤． 一种带有动态输出反馈控制器的网络控制系统的Markov 跳变模型［J］．自动化学报，2009，35(5):627 -631．

［14］ HE Xiao，WANG Zi-dong，JI Y D，et al． Networkbased fault detection for discrete-time state-delay systems:A new measurement model［J］． International Journal of Adaptive Control and Signal Processing，2008，22(5):510 -528．

［15］刘艳红，罗永平，刘言兴． 基于改进型JGPC 的网络系统随机时延补偿［J］． 郑州大学学报:工学版，2014，35(1):30 -33，38．

［16］肖小庆，周磊，陆国平． 带有随机时延的非线性网络控制系统的输出反馈镇定［J］． 控制理论与应用，2009，26(9):1023 -1025．

［17］史永宏，高世界． 基于Smith 的自适应模糊网络拥塞控制算法［J］． 计算机应用研究，2013，30(10):3071 -3074．