基于轴向偏差的飞机数字化装配定位基准建模
胡玉龙,王仲奇,李西宁,康永刚
HU Yu-long, WANG Zhong-qi, LI Xi-ning, KANG Yong-gang
(西北工业大学 现代设计与集成制造技术教育部重点实验室,西安 710072)
0 引言
早期飞机装配过程中,针对不同的装配件设计不同的工装,甚至有时不同的加工余量也要设计不同的专用工装,因此需要设计的工装多,生产准备周期长,成本高。采用数字化装配工装以后,如壁板件的装配,不仅可以大大提高工作效率,而且由于其灵活性可以适用于不同壁板件的装配,减少了工装的数量。对于不同形状的壁板,也很容易实现定位装夹,进而便于实现自动铆接装配。如果再与计算机等终端设备相连,则可将装配件三维数字模型直接输入计算机来操作数字化工装设备[1,2]。
飞机数字化装配中的定位过程如图1所示,主要包括理论装配定位信息的提取、现实装配定位工步固定参数的测量、现实装配定位基准的建立、装配定位工步信息的获取以及数字化装配设备实现装配定位动作的驱动等内容。
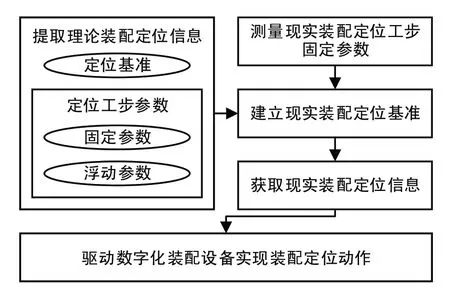
图1 飞机数字化装配中的定位过程
随着数字化装配工装的设计应用,飞机的装配方式开始展现柔性特征,而针对不同的装配目标,与之相对应的飞机数字化装配环境往往并不尽相同,数字化装配测量设备开始应用于装配过程中装配定位基准的测量[3,4]。由于基于传统意义上的数字化测量手段,飞机数字化装配过程中测量结果也主要采用最小二乘法或加权最小二乘法对测量参数组成的超定方程进行求解[5,6],虽然最小二乘法的计算程序实现简单,但却导致从计算结果上部分定位点的误差处于约束的极限位置。
本文主要通过分析现有基于最小二乘法或加权最小二乘法的飞机数字化装配定位基准模型,结合装配中线定位的特征,提出了一种基于轴向偏差的飞机数字化装配定位基准模型,并对该模型的求解以及应用进行分析,最终通过某型飞机的壁板组件装配预定位的定位基准建模进行算例分析,验证其合理性。
1 飞机装配定位基准分析
在装配中,工艺基准按功能分为定位基准、装配基准、测量基准以及混合基准。定位基准是指用以确定结构件在设备或工艺装备上的相对位置的基准[7,8]。因加工、装配等实际系统中存在的误差因素(如装配夹具的误差、零件制造误差及在装配夹具中的定位误差等等),理论定位基准对应实际系统中的定位基准并非完全精确,如何在不对零部件、装配夹具等进行物理修正的情况下,保证装配准确度(如气动外缘准确度、部件相对位置准确度、内部结构件位置准确度、结构件配合准确度以及部件功能性准确度等)达到最优值,飞机数字化装配中定位基准获得所面对的重要问题之一。
飞机数字化装配定位基准的表示是定位基准建模的第一步,飞机数字化装配定位基准建模的本质属于装配定位环境特征提取与知识表达方法的范畴,决定了定位工步参数如何存储、利用以及获取知识。识别飞机数字化定位基准模型的目的是供飞机数字化装配设备进行工艺路径规划,因此定位基准模型必须便于机器理解和计算,且当新的装配工艺环境信息出现时,应该能够方便的更新定位工步参数。因此,采用世界坐标系中的坐标信息来描述装配定位环境的特征。
在统一世界坐标系下,飞机数字化装配定位基准的建模主要涉及到理论装配环境(Theoretical Assembly Environment,TAE)与现实装配环境(Actual Assembly Environment,AAE)两部分,如图2所示。两种装配环境中均包括可实时调整部分、非实时调整部分以及装配基准(以下用AD表示),考虑它们对定位工步参数的影响,将定位工步参数分为浮动参数(可调整工步参数,用VP表示)与固定参数(不可调整工步参数,用SP表示)。
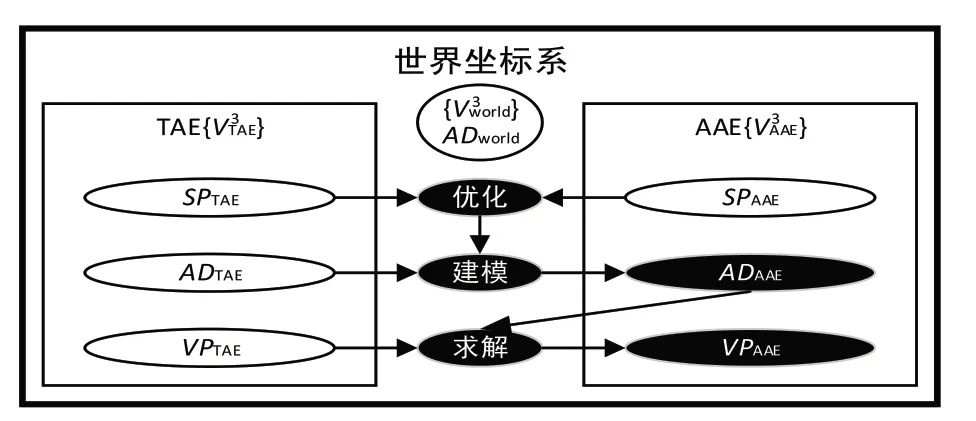
图2 飞机数字化装配工艺基准
一般情况下,已知TAE下ADTAE,SPTAE,VPTAE等参数,AAE下测量获得SPAAE,将人工调整SPAAE与求解ADAAE的过程称为装配定位基准建模,并在获得ADAAE的基础上求得AAE下的VPAAE的过程称为定位工步参数求解。
2 基于轴线偏差最小的定位基准建模
2.1 基本假设及说明
1)认为可以保证在一次装配基准建模的过程中现实装配环境保持足够的稳定性,且在没有人工调整及可控运动情况下,保证SPAAE与VPAAE等参数的变化误差远低于装配定位要求的装配精度;
2)认为测量设备的测量误差远低于装配工艺要求的装配精度,认为测量误差为0;
3)认为SPAAE对于实际装配测量情况的误差远低于装配定位要求。
2.2 定位误差指标分析
由分析可知,为保证整个装配过程的定位精度,定位基准应在保证设计公差的基础上,尽量接近使得形状误差最小,以保证装配定位中对结构件施加的变形最小,从而保证装配完成后装配件的应力影响最小。
1)形状误差评定的基本准则
形状误差是实际被测要素的形状对其理想要素的变动量,而理想要素的位置应该满足最小条件。所谓最小条件,是指实际被测要素对其理想要素的最大变动量为最小。此时,形状与公差带相同且包容实际被测要素的区域为最小,该最小包容区的宽度或直径就是实际被测要素的形状误差[9]。
对于中心要素,符合最小条件的理想要素位于实际被测要素之中,并使实际中心要素对理想要素的最大变量为最小,如图3所示。

图3 中心要素的最小条件
2)定位面误差性能分析
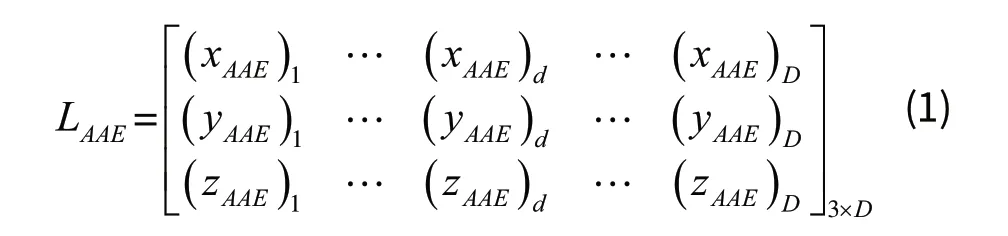
根据形位误差中中心要素偏差评定的准则,取轴线偏差为到定位线空间垂线距离,其误差性能 lΔ (其中El是该定位线的误差限)为:
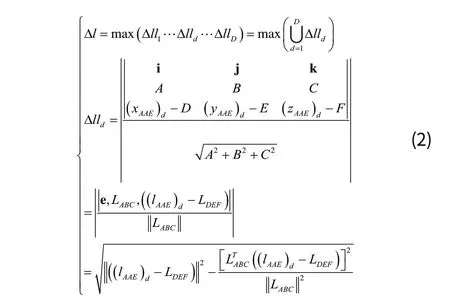
其中,e是单位列向量。(注:行列式与其转置行列式相等)
3)定位点误差性能分析
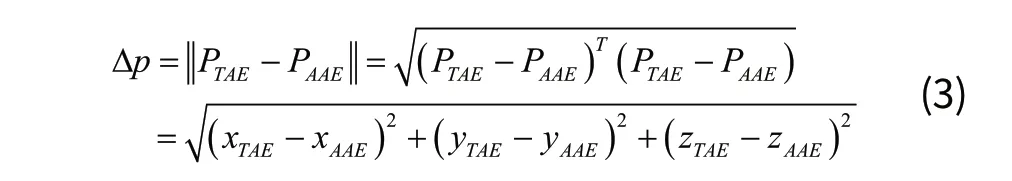
4)总体性能分析
对于Nl个定位线与NP个定位点,则有总体误差性能
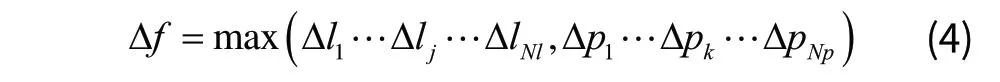
实际中,不同定位线与定位点的误差限往往并不完全相等,考虑不同误差限下的总体性能,则有总体误差性能
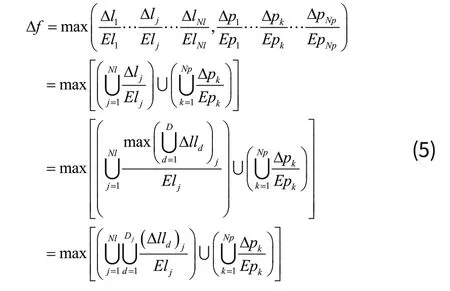
其中:Dj表示第j个定位线所对应的离散测量点的总数;表示第j个定位线中第d个离散测量点到该定位线的误差;Elj是第j个定位线的误差限;是第k个定位点的定位误差;Epk是第k个定位点的误差限。
2.3 建模中涉及的变量
1)定位基准表述
对于空间中不同坐标系的描述,往往包括位置描述与方位描述两部分,由此类推给出定位基准的描述。
AD为坐标系原点O=[a, b, c]T与轴XYZ转角Ro=[α, β, γ]T转角等特征的集合。
对于原点O认为有:
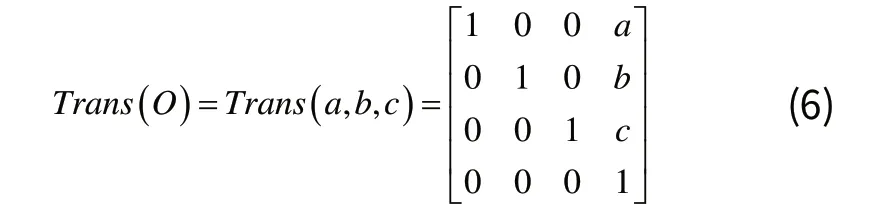
对于转角Ro认为有:
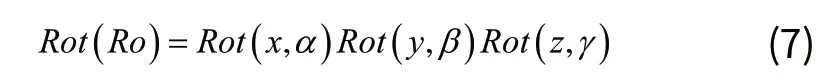
其中:
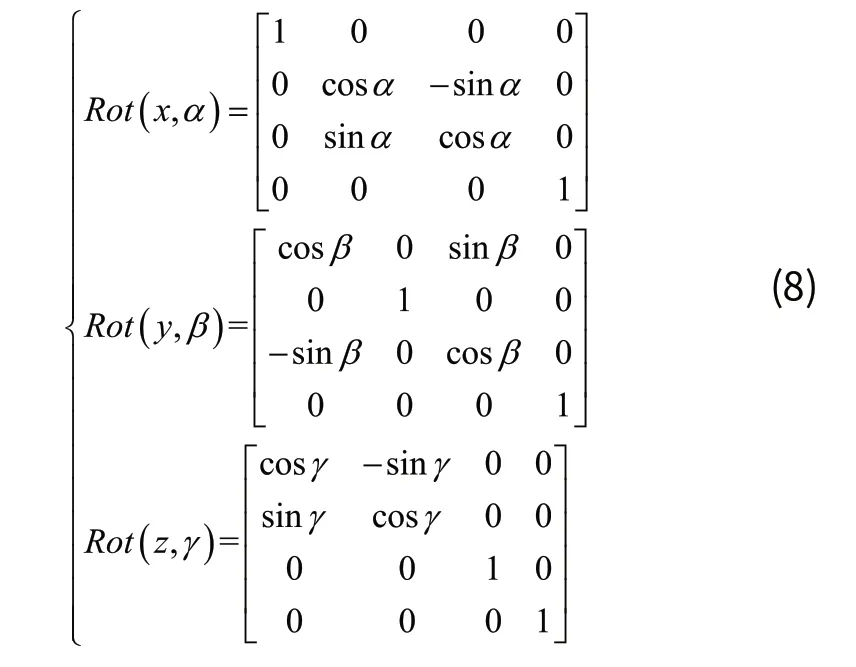
因此对于集合AD可简化定义为变换矩阵形式T:
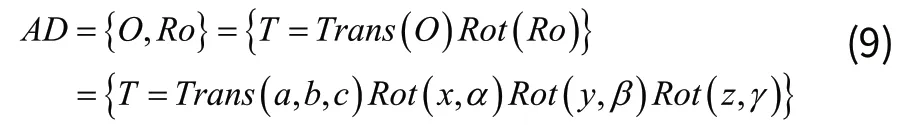
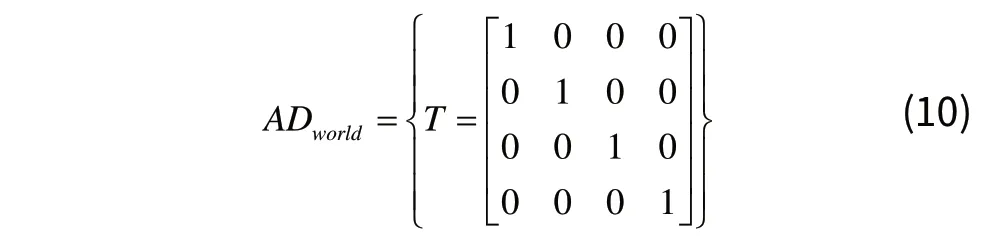
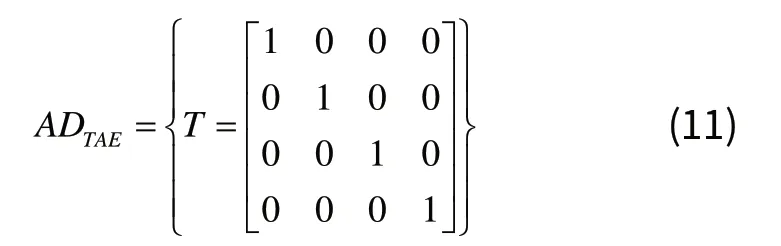
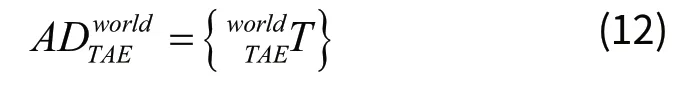
其中:
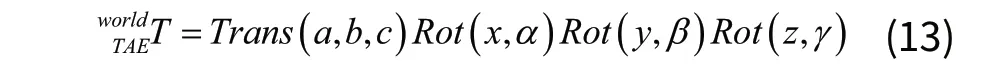
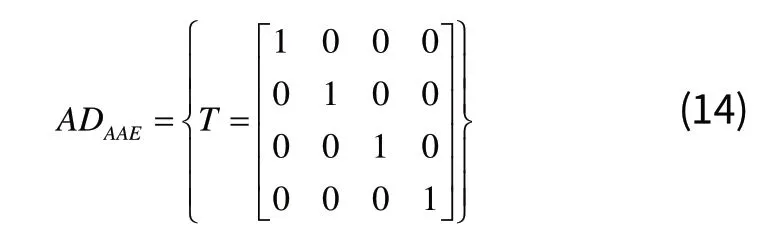

其中,f为定位误差性能指标的优化函数。
2)定位工步参数表述
定位工步参数SP主要包含定位点、定位线等元素的表述,定位工步参数VP主要表达为定位点,其中,SP有定位点N个,定位线M个,VP有定位点L个。
SPTAE表述为:

VPTAE表述为:
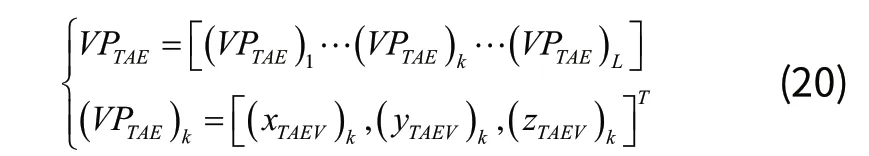
VPAAE表述为:
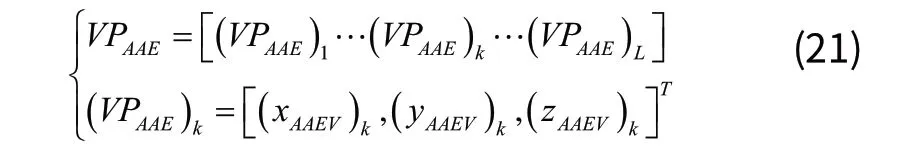
SP定位线误差限表述为:
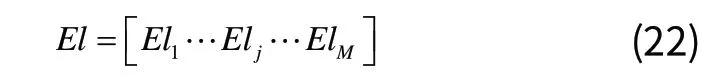
SP定位点误差限表述为:
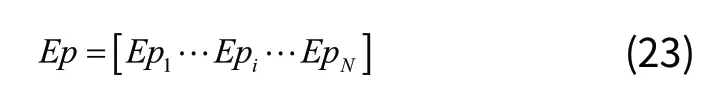
3)建模变量分析
除ADworld、ADTAE、ADAAE等常量外,设计的变量涵盖装配定位基准建模与定位工步参数求解两方面。
装配定位基准建模中涉及的参数:
装配定位基准建模中,已知参数包括:ADTAE下的的以及El和Ep,求解装配基准
定位工步参数求解涉及的参数:
2.4 目标函数
目标函数为实际测量环境下的定位误差,根据公式(5)容易建立获得ADworld下的目标函数:
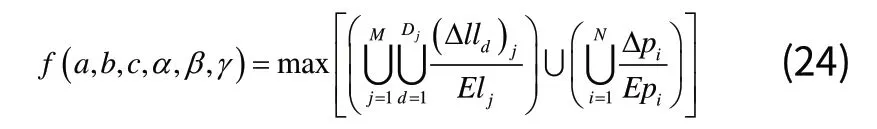
其中,在ADworld下:
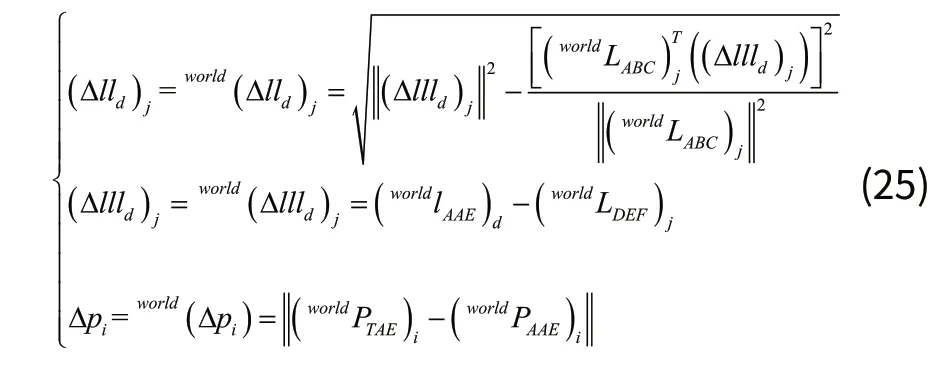
由于SPTAE中的LTAE表示的是定位直线的直线方程,在存在的情况下,无法直接对进行齐次变换,形式如公式(25)的无法进行求解,所以需要对公式(25)进行等价变换。
由于在线性空间中,对于不同笛卡尔坐标系下,相同元素在公式(2)与公式(3)中的结果不变。即对任意装配基准有:
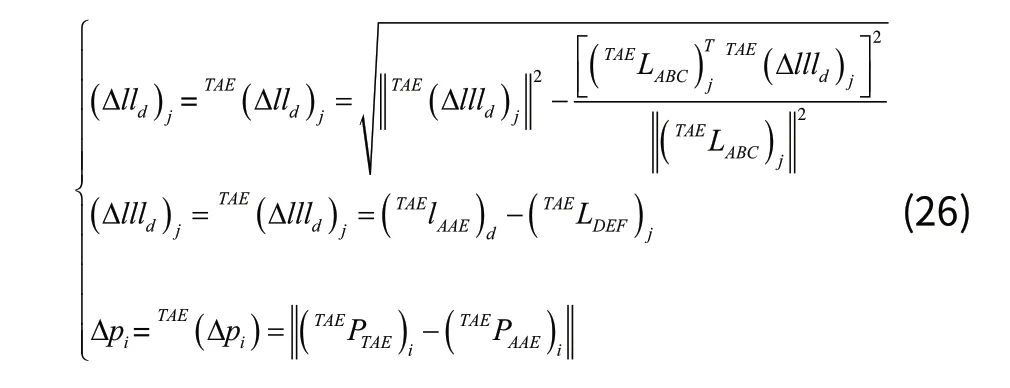
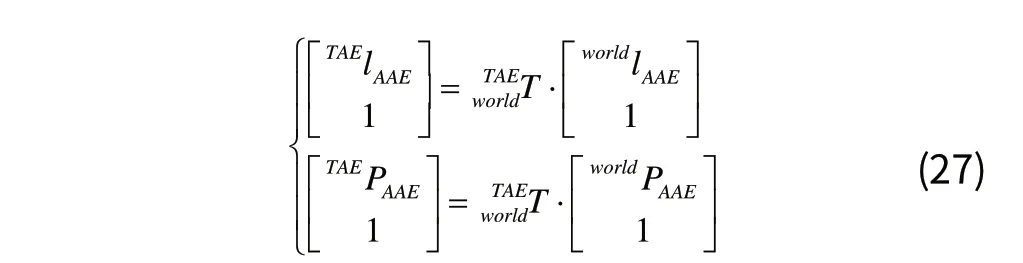
其中,根据齐次变换的逆变换有:
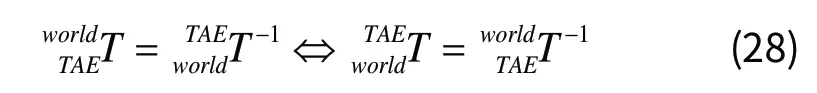
合并公式(26)、公式(27)、公式(28)得到:
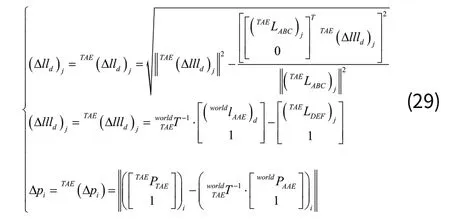
2.5 约束条件
对于等坐标系基准变换参数,应满足:

此外,各个定位点及定位线应满足各自的误差限的要求,即:
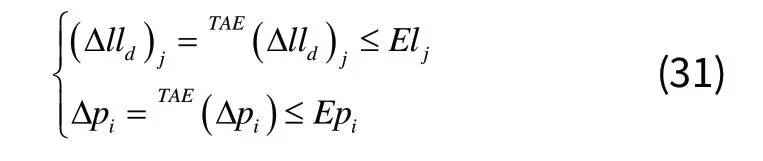
3 装配定位基准模型及工步参数求解
3.1 飞机装配定位基准模型
作为最优化设计的模型,基于轴线偏差最小的装配定位基准模型的一般形式由设计变量、目标函数和约束条件3部分组成,总结第二章的建模过程,得出飞机装配定位基准模型。
极小化设计的基准模型为:
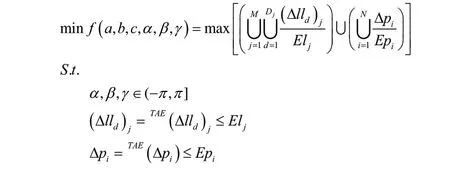
其中:
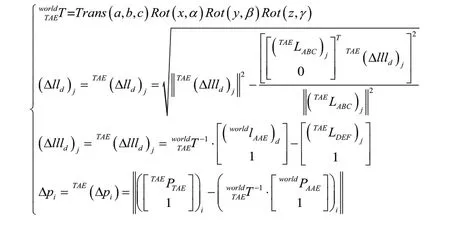
作为最大值最小化的优化问题,需要采用极小化极大(Minimax)算法才能实现,可采用粒子群(PSO)算法进行寻优求解[10,11]。
3.2 定位工步浮动参数求解

4 模型应用算例分析
通过某型飞机的壁板组件装配预定位柔性工装进行算例分析,该装配工装适应某型飞机的中机身8块壁板的预装配。以前上右刀型壁板的装配预定位为例,进行定位基准模型的验证。该前上右刀型壁板主要由刀型蒙皮、8行长桁共14根(航向上有截断)组成,如图4所示,壁板的预装配工作主要完成蒙皮与长桁的预连接。

图4 前上右刀型壁板结构
为保障前上右刀型壁板蒙皮的精确定位,在端卡板处设置蒙皮端挡块定位蒙皮的X向,在内存卡板下方设置蒙皮卡块以保障蒙皮的Z向,为保证蒙皮的气动力外形在蒙皮定位时使用蒙皮拉紧带使蒙皮紧贴于内型卡板表面,如图5所示。
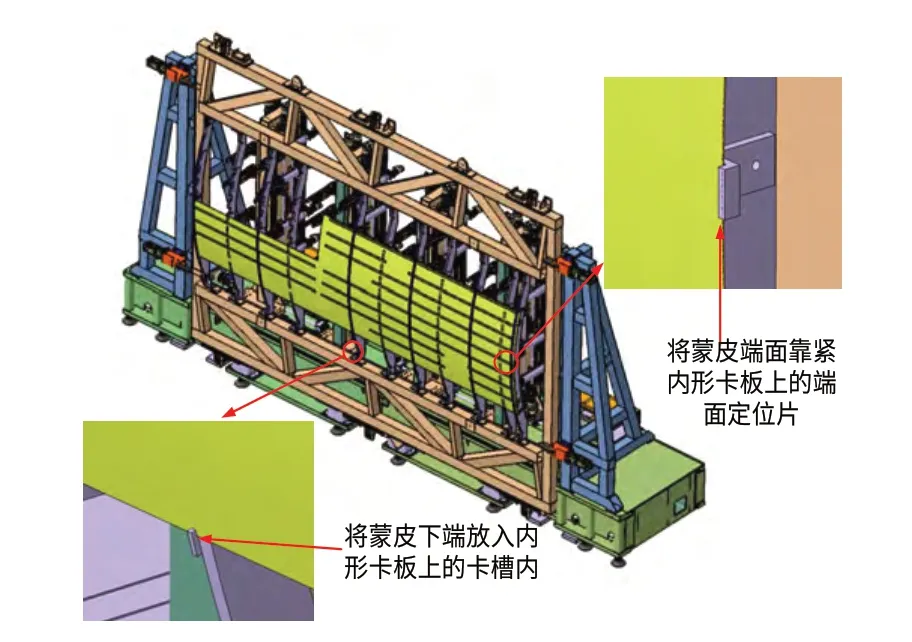
图5 前上右刀型壁板的蒙皮定位
由于卡板是前期定位安装,无法实时调整,所以通过卡板采集SP参数,进行定位基准建模。有定位点3个,定位线3个,以下单位均为mm。SPTAE为:
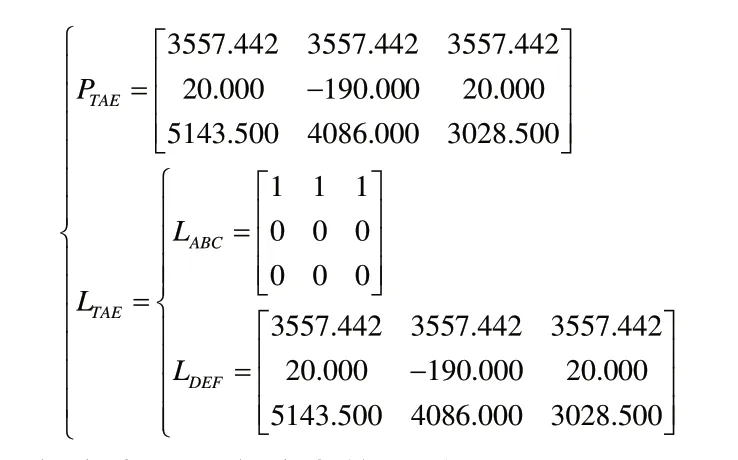
SP定位线以及定位点的误差限为:
El=[0.500 0.500 0.500]
Ep=[0.500 0.500 0.500]
长桁的定位是通过可实时调整的长桁夹持器夹持定位,如图6所示。

图6 前上右刀型壁板的长桁定位
通过得到的定位基准计算25个长桁夹持器的定位工步浮动参数VP,实现长桁的装配预定位。VPTAE为:
通过激光跟踪仪测量需要的SPAAE,数据在SA软件中的情况如图7所示。
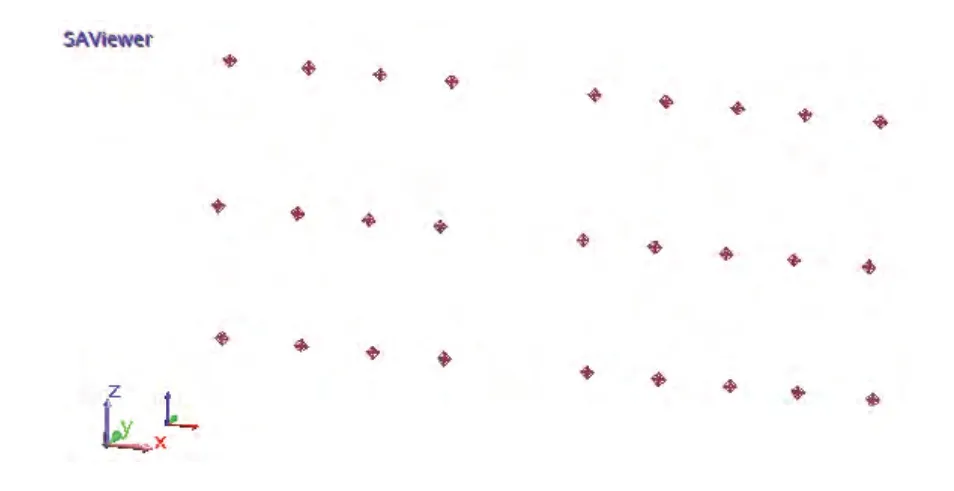
图7 API激光跟踪仪测量的SPAAE参数
得到的SPAAE为:


经计算得到优化结果,当:

时,有优化值:
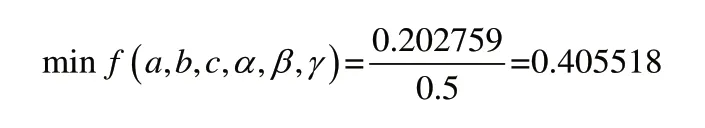
得到定位基准:

根据求解得到的定位基准,得到实际定位工步浮动参数VPAAE:
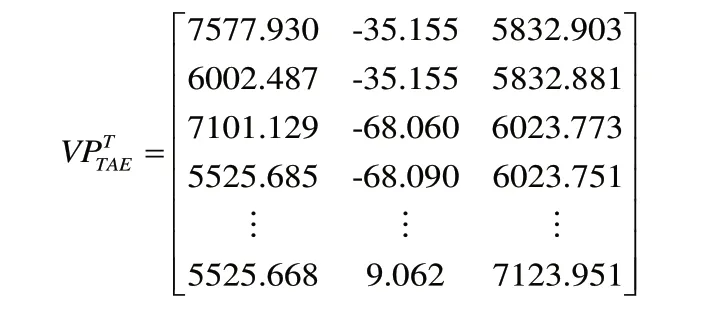
并根据得到的定位工步浮动参数VPAAE,协调激光跟踪仪,编辑装配工艺轴组参数,如图8所示。
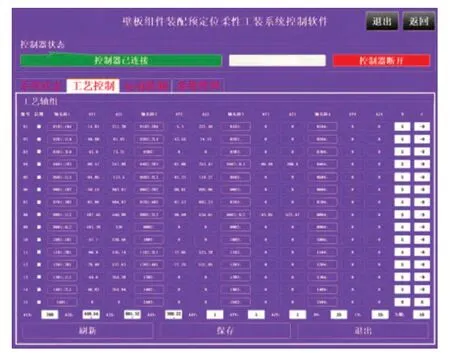
图8 编辑工艺轴组
5 结束语
通过基于轴向偏差最小建立的飞机数字化装配定位基准模型,改变了传统上采用最小二乘法进行定位基准建模的现状,使得在本基准模型下的装配定位误差分配更为合理,同时保证了飞机数字化装配过程中的目标定位点的有效计算。
[1] 范玉青,梅中义,陶剑.大型飞机数字化制造工程[Z].北京:航空工业出版社,2011.
[2] Kihlman H,Ossbahr G,Engstrm M,et al. Low-cost automation for aircraft assembly[R].SAE Technical Paper,2004.
[3] Junbai L,Kai Z.Multi-point location theory, method, and application for flexible tooling system in aircraft manufacturing[J]. The International Journal of Advanced Manufacturing Technology.2011,54(5-8):729-736.
[4] Millar A,Kihlman H. Reconfigurable flexible tooling for aerospace wing assembly[R].SAE Technical Paper,2009.
[5] Tian S, Lu W,Tian H, et al.Comparing evaluated precision of straightness error among two spot, least square method and minimum envelope zone method[C].IEEE,2010.
[6] Wang C,Qi F,Shi G, et al. A linear combination-based weighted least square approach for target localization with noisy range measurements[J].Signal Processing.2014,94:202-211.
[7] Mei S, Tiechang H X Z.Assembly Modelling Based on Assemby Feature[J].China Mechanical Engineering.2001,9:16.
[8] 航空制造工程手册总编委会.航空制造工程手册.飞机装配[M]. 2版.北京:航空工业出版社,2010.
[9] 王玉,刘笃喜,蔡安江.机械精度设计与检测技术[M].北京:国防工业出版社,2008.
[10] Noel M M. A new gradient based particle swarm optimization algorithm for accurate computation of global minimum[J]. Applied Soft Computing.2012,12(1):353-359.
[11] Tasgetiren M F, Liang Y,Sevkli M,et al.Particle swarm optimization algorithm for makespan and maximum lateness minimization in

