某商用车车身动态特性及疲劳耐久预测
周 鋐,刘 浩,张 辉
ZHOU Hong1,2, LIU Hao1,2, ZHANG Hui3
(1.同济大学 汽车学院,上海 201804;2.同济大学 新能源汽车工程中心,上海 201804;3.北京航天发射技术研究所,北京 100076)
0 引言
车身是商用车的重要组成部分,属于大型的薄壁构件,它不仅是一个汽车品牌的标志和象征,更是一个公司汽车设计研发水平的体现[1]。车身在路面动态激励的情形下,其动态特性—固有模态决定了车身抵抗变形的能力[2]。表征车身抵抗受到外界载荷的能力—疲劳耐久特性对于车身在长期使用过程中的质量影响是很大的。传统的车身疲劳耐久试验在试验场进行,试验周期长,因此,运用仿真手段对车身动态特性及疲劳耐久进行预测不仅可以降低开发经费又可以缩短研发周期,在激烈的市场竞争中对汽车制造厂商有非常重要的意义。
1 车身有限元模型的建立
精确可靠的车身有限元模型是车身疲劳分析的关键,因此需要建立准确的白车身有限元模型。首先将白车身CAD模型在CATIA软件中生成IGES格式的文件,然后再导入有限元分析软件Hypermesh中进行网格的划分。
有限元分析中最重要的部分是网格单元的划分,选择合适的网格单元类型对有限元分析的准确性有着非常重要的影响,网格单元的类型决定了分析的可靠程度,网格单元的数量决定了分析工作量的大小[3]。白车身是由复杂的薄壁曲面板件焊接组合起来的结构,在汽车行驶过程中各个部件都有可能会产生扭转、弯曲等复杂的变形。因此,选择2D单元即壳单元作为白车身部件的主要单元类型。壳单元与实体单元不同,它的厚度是独立于结构的常数,白车身模型全部由面组成,每个面的厚度根据实际的部件来定义。将厚度作为独立的参数可以方便的对其修改及进行后续的优化;壳单元遵循壳理论,能很好的处理弯曲和剪切效应。
单元的划分过程是将每一个部件的几何模型导入到Hypermesh中,通过自动或者手动的方法进行网格划分,选择的基础网格类型为四边形壳单元,大小为10mm。
网格划分的过程中最重要的是保证具体单元的质量,因此,在对每一个部件进行网格划分的过程中都需要对单元的质量进行检查。检查标准如表1所示。

表1 网格质量检查标准
同时需注意的是,在网格划分的过程中应尽量多的使用四边形的网格,减少三角形网格的使用数量。
白车身一共由300多个部件组成,它们通过各种不同的连接方式相连包括:胶接、螺栓连接、点焊等,用的最多的是点焊,选择合适的连接方式模拟部件之间的连接对仿真结果的精确性和准确性也是至关重要的。
本文选择Hypermesh软件中的CWELD单元来模拟车身的点焊,CWELD单元可以用来模拟焊接中可能存在两个部件相连的两层焊接,也可以用来模拟三个部件相连的三层焊接。
根据以上的建立方法,对每个部件划分网格,附以材料属性,再根据实际生产过程中的焊点布置位置将各个部件进行连接装配,最终获取白车身有限元模型,整个模型包括643925个网格。
材料参数为:杨氏模量E=2.1×105Mpa,密度ρ=7.9×10-9t/mm3,泊松比μ=0.3。建立的有限元模型如图1所示。

图1 白车身有限元模型
该商用车车身为非承载式结构,白车身主要由以下几部分构成:顶棚总成,地板总成,前围防火墙总成,裙边总成,侧壁总成。
2 白车身模态参数的计算
2.1 仿真模态计算
在Hyperworks-Optistruct软件中对处理过的白车身模型进行模态仿真分析,计算自由状态下的白车身固有模态。由于车身的振动主要受较低的频率的影响,并且路面的激励频率一般低于50Hz。因此,计算频率定在50Hz以下,重点考察仿真得到的车身前四阶模态参数,仿真获取的白车身前四阶模态参数及振型如表2所示。
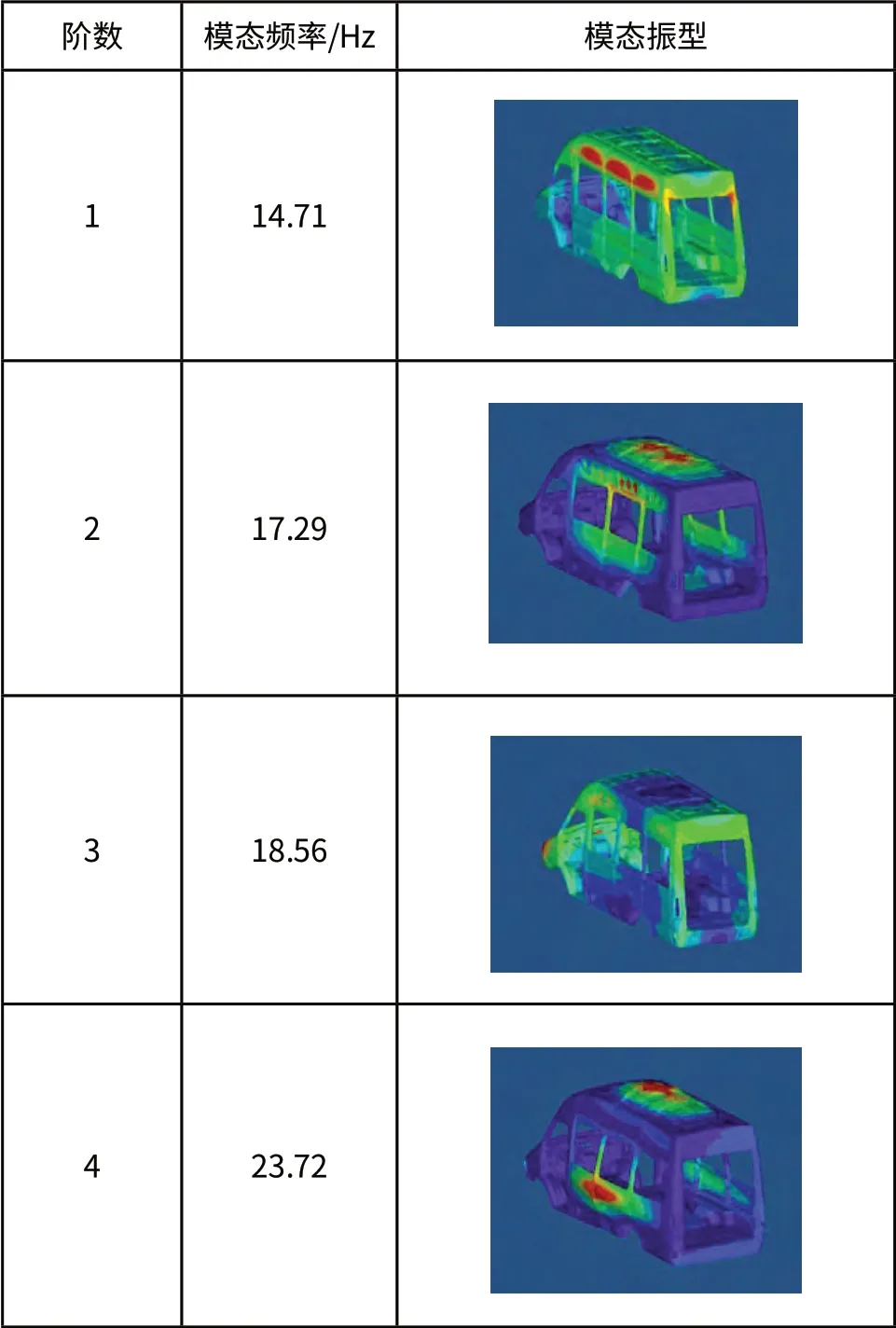
表2 仿真获取的白车身前四阶模态参数及振型
2.2 仿真模型的试验验证
试验采取自由支撑方式,分别在前门栓和后门栓位置使用橡皮绳将车身悬吊。保证悬挂最高刚体模态低于2Hz,不会对第一阶变形模态产生影响[4],悬吊方式如图2所示。

图2 白车身悬吊方式示意
本次试验除3个激振点外共安排布置了307个测试点,对这些测点分别进行x、y、z三个方向的振动加速度信号的采集。测点布置如图3所示。

图3 白车身测点布置图
通过试验模态分析可以校验仿真模态,通过LMS的Polymax算法进行模态定阶。
将试验获取的白车身前四阶模态参数与仿真相比较,结果如表3所示。
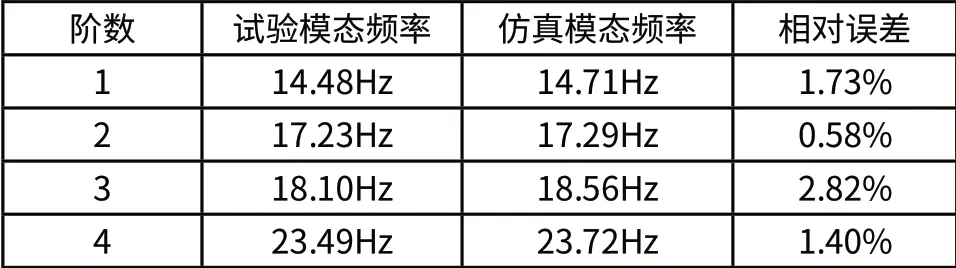
表3 试验和仿真模态参数对比
试验和仿真的模态频率相对误差在3%以内,且各阶模态振型也有很高的相似度,可以认为建立的有限元模型是可靠的,能够很好地反映实际白车身的动态特性,可以用于后续的疲劳仿真计算。
3 车身疲劳耐久分析
运用先进的计算分析软件,汽车车身的疲劳寿命一般分析步骤如下:
1)通过计算得到关键零部件的边界载荷条件;
2)通过有限元软件Nastran计算车身的特定参数,并作为后续疲劳计算的载体;
3)通过Nastran计算有限元模型在单位静载荷下的应力模态;
4)结合载荷的时间历程,以及零部件的材料疲劳特性,如S-N曲线,通过LMS Virtual.lab Durability Analysis模块计算得到关键零部件的疲劳损伤分布情况。
研究的商用车车身和车架相连,边界载荷条件为连接点的激励力。因此,下面对激励力进行计算。
3.1 边界载荷的计算
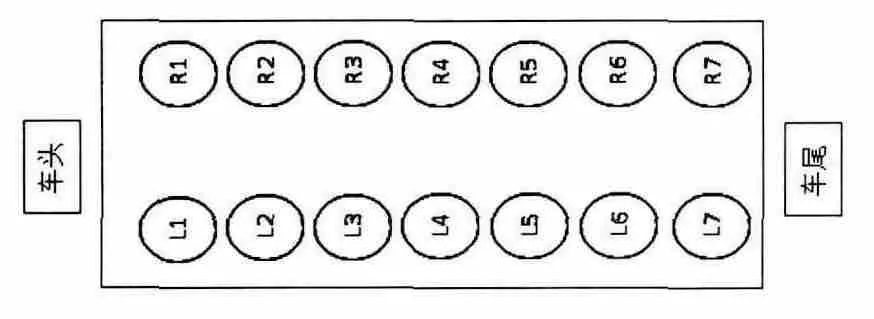
图4 车身与车架连接位置示意图
图4 所示为商用车车身与车架连接位置示意图。车身通过以上14个连接点与车架相连接,车架通过这些连接位置向车身提供激励力。汽车在实际行驶工况下,路面不平度通过车架向车身进行传递。因此车身的振动疲劳可以看作主要是由车身与车架的连接位置的激励力引起的。
每个激励力可能会通过不同的路径作用于车身,例如,L1位置对L1位置会产生激励,同时也会对其他13个连接点产生激励。车架对车身的这一作用称为振动激励,其传递过程称为结构传递。每个连接点考虑x,y,z三个平动自由度的激励忽略转动自由度的激励。本文就是基于传递路径建立激励力计算模型的。
对于线性函数y=kx+b,只要任意给定一个自变量x,便可求得y。当k≠0时,其反函数存在:x=(y-b)/a。根据反函数,只要知道任意函数值y便可求得自变量值x。逆矩阵法的原理类似于通过反函数来求自变量[5]。对于某一振动的线性系统,当有激励力F1,F2,…,FN存在时,存在响应A1,A2,…,Am由系统的运动方程可得:
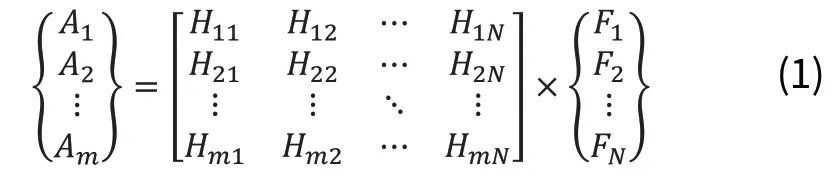
因此,耦合激励力可用下式估计:
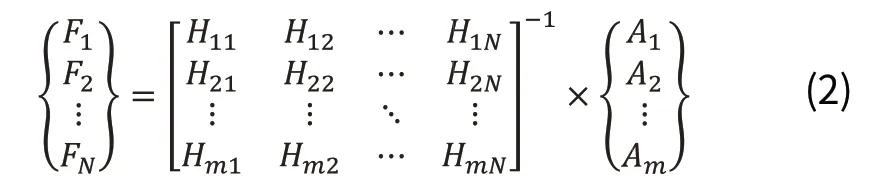
上式可简写为:
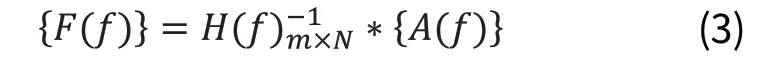
其中{F(f)},为耦合激励力向量;{A(f)}为工作状态下的响应向量,称A1,A2,…,Am为参考自由度;Hij=Ai/Fj为由输入Fj到响应的Ai频响函数(传递函数)。由于响应的形式可以多样,如加速度、速度、位移,因此,传递函数也有三种形式:力—加速度、力—速度、力—位移。本文试验过程中得到的是力—加速度传递函数。
此外,在使用逆矩阵法计算激励力时还应考虑以下几点:参考自由度须设定在受动方,尽可能的分布在耦合点附近;测量频响函数HmN时,主动方应在各耦合点处与受动方解耦并从耦合点移走,以消除激励源耦合的影响;有时需要根据耦合点处的结构形式制作相应的连接件,如质量块等,用于力锤施力,安装加速度传感器或者激振器等。
完成传递函数的计算后,在同济大学四通道轮耦合道路模拟试验台上进行道路模拟实验,试验的加载谱,是安徽定远试车场上采集的道路载荷谱,在上述连接位置贴好三向加速度传感器,在车身关键位置贴好应变片,对上述信号进行采集。然后利用传递路径模型可以对激励力进行计算。
3.2 车身疲劳计算
已经得到了精确的车身有限元模型,并且通过逆矩阵法得到了车身疲劳计算的边界条件,本次仿真过程中涉及的算法如表4所示。

表4 仿真计算中的算法汇总
首先根据车身所受的载荷数,对车身有限元模型以准静态算法分别求取每个边界载荷自由度在单位力作用下的应力响应,即可得到单位载荷影响因子。然后采取激励力对14个连接点进行相应的受力加载,然后对各个边界载荷与单位载荷影响因子相乘并线性叠加,结合材料的疲劳参数,就可以得到基于准静态叠加法的车身疲劳损伤云图,如图5~图7所示。

图5 车身疲劳损伤云图

图6 后车门四角疲劳损伤云图

图7 防火墙损伤云图
从得到的损伤云图可以看出,总体上,车身结构损伤分布相对集中,主要集中在前挡风玻璃安装处的四角、防火墙处、车身与车架连接处、以及后车门四个角,其损伤值要略大于其他位置,即云图的颜色相比其他位置更偏暖色。
部分测点的仿真应变云图如图8~图10所示。

图8 防火墙内部仿真应变云图

图9 结构孔仿真应变云图

图10 左横梁仿真应变云图
在四通道轮耦合道路模拟试验中已经记录了关键部位的应变信号,此处将作为对比数据用来验证疲劳预测的有效性与可信度。
结合材料的疲劳参数以及测点的应力应变雨流矩阵,通过累计损伤理论,就可以得出测点部位的损伤及其寿命[6,7]。
取用材料的参数,疲劳极限SE=160Mpa,循环次数NE=5×106,S-N曲线斜率为5,则S-N曲线满足式(4),所得的疲劳寿命曲线如图11所示。


图11 材料的S-N曲线
采用LMS Virtual.lab对车身进行疲劳仿真的计算,得到了防火墙内部、结构孔和左横梁三个关键点的损伤值与寿命大小,及其与仿真结果的对比,如表5所示。
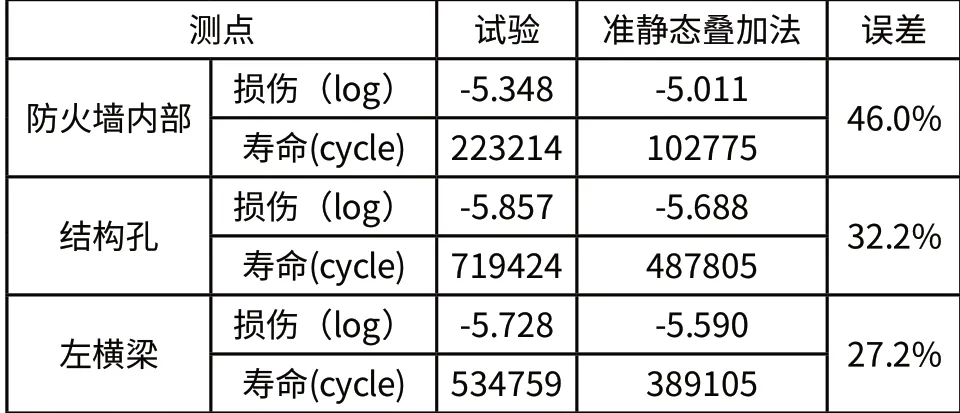
表5 仿真与试验的应变损伤对比表
从表5中,可以看到试验测得的损伤值与仿真求得的损伤有所偏差,但是寿命的数量级基本一致,试验得到的损伤值和仿真得到的损伤值差异不大,可以认为仿真是准确的。
偏差的原因分析:在应变试验中,把部分位置简化成了单向应力状态,采用单应变片测量的方法,而在有限元疲劳分析中单元拥有厚度信息,而呈三向应力的状态,所以可能会导致仿真计算的主应力偏大。
通过对比分析,可以发现本文提出的用逆矩阵法求解激励力的方法具有较高的可信度。在实际的工程应用中具有一定的指导意义。
4 结束语
采用有限元技术对车身的模态及疲劳耐久特性进行分析具有可行性,但是试验验证也是必不可少的。采用逆矩阵法求解车身的边界载荷条件是准确可行的,可以节省很多的人力物力。
通过LMS Virtual.lab软件进行车身的疲劳仿真为车身的优化设计提供了指导,也为汽车其他部件的优化计算提供了帮助。
[1] 庞剑,谌刚,何华.汽车噪声与振动——理论与应用[M].北京:北京理工大学出版社,2006.
[2] 毛彩菊,王艳.车身的模态分析及疲劳寿命计算[J].制造业自动化,2011,11:105-108+125.
[3] 周鋐,刘浩,吴亚波,范昊天.基于试验与仿真的扭转梁式后桥模态分析与优化[J].机电一体化,2014,09:8-12.
[4] 任永连,周鋐,束元.基于质量线法的汽车动力总成刚体惯性参数的研究与辨识[J].汽车技术,2013,07:25-29.
[5] 王思乐,周鋐.基于结构传递路径分析的某客车悬置优化[J].佳木斯大学学报(自然科学版),2013.
[6] LMS International. LMS耐久性新技术及其应用[Z].2005.
[7] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003.

