摇臂式履轮转换机构的设计与分析

黄 彬，朱文博，刘立成

HUANG Bin, ZHU Wen-bo, LIU Li-cheng

（武汉理工大学 物流工程学院，武汉 430063）

0 引言

随着机器人技术的不断发展，机器人在工业生产中已得到广泛地应用[1]。但是面前很多机器人为固定位置的机器人，它们的移动范围收到很大的限制，不方便适用于各种应用场合。为了满足社会各种发展应用的需要，出现了各种移动是机器人。如轮式机器人具有速度快、效率高、易平衡、稳定性好、以控制、技术较成熟，实现机构相对简单等优点，但其对路况要求高，适应力差。而相对的履带式机器人野外作业能力强，对路况要求较低，但其效率低[2]。为了弥补轮式和履带式行走机构的不足，对摇臂式行走机器人进行研究，探讨了摇臂式履轮机器人的移动系统及结构，提出一种转换机构。

1 摇臂式履轮转换机构的设计

为实现履带与轮子的转换功能，我们所设计内容是，将机器人的四个轮子固定在底盘上，让履带可以升降，当履带平面低于轮子平面时，实现轮子向履带转换的过程，反向，可实现履带向轮子的转换过程。

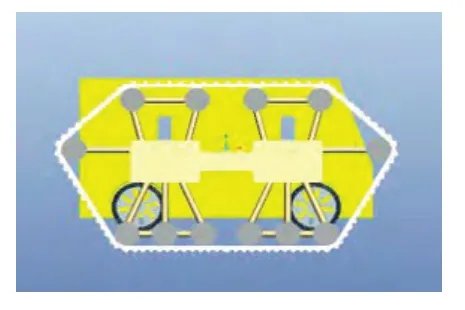
图1 履带工作

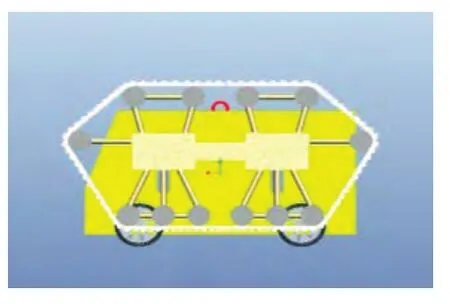
图2 履带闲置

1.1 履带支撑架设计

为了实现履带的升降，传统的履带固定方式并不可行，所以我们设计了一种新型的支撑架，该支撑架为左右对称结构，包含两个六角支撑轮系。安装时，将一对履带支撑架安装在车体的两侧。之所以在支撑架中包含两个支撑轮系，其目的是为了保持力矩的平衡。

考虑到支撑架总体的空间问题，以及带轮的同步转速问题，不可能令每个履带轮都为主动轮，所以我们便设定支撑架最左侧和最右侧的履带轮为主动轮，这样还可以保持良好的平衡度。

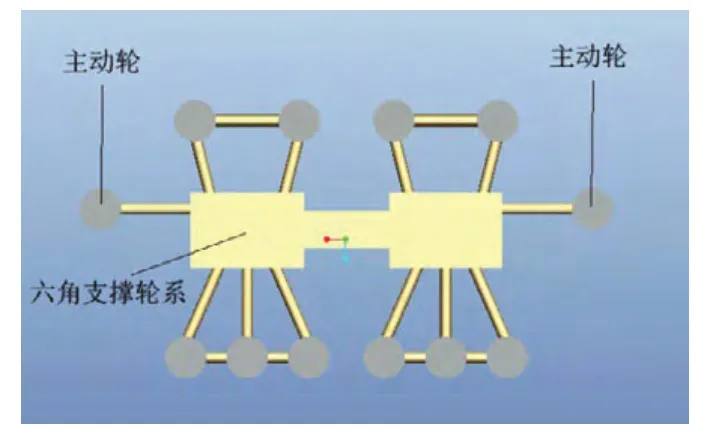
图3 履带支撑架

为了使履带只可以在竖直方向运动，所以我们为支撑架的中心部分设置了一个滑块，它由工字型杆与支撑架主体相连，与滑块对应的是在机器人车厢两端各设定了一条滑道。

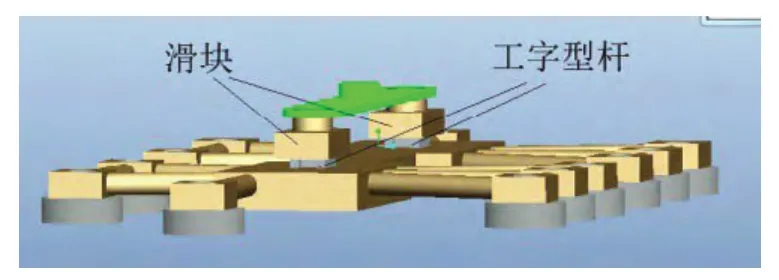
图4 支撑杆的另一角度视图

机器人小车中的动力来源一般为舵机或电机的旋转运动，为了将舵机的旋转转换为支撑架的直线运动，配合车厢滑道与支撑架上的滑块，我们应用了曲柄滑块机构，该机构工作状态及其稳定且机构简单。我们将曲柄与连杆设定在了车厢的内部，这是因为如果放在外部，会对履带的运动产生严重的干涉。

由于滑道行程有限，所以滑块的运动存在极限位置，当滑块处于最上端时，履带处于闲置状态，当滑块处于最下端时，履带处于工作状态。也就是说，舵机控制曲柄的旋转运动，必须在一定的角度范围内运动，角度变化量为定值。所以，为了方便舵机旋转角度的控制，对曲柄和连杆长度进行计算后，曲柄、连杆的设置效果为，当曲柄与连杆处在一条直线时，滑块处于下极限行程位置，履带工作；当曲柄与连杆重合时，滑块处于上极限行程位置，履带闲置。

图5 滑块下极限行程位置

图6 滑块上极限行程位置

也就是说，舵机的旋转变化角度为180°，这是一个比较容易控制的特殊值，舵机主轴的单向旋转就可实现滑块的往复运动，可不必变换转向。同时这种结构的设计可以保证机构运动无死点，防止舵机卡死。

1.2 锁死机构设计

履带一般工作在崎岖不平的道路，会上下震动，单纯的靠曲柄连杆机构支撑受力是不行的，而且，当履带闲置时，因其整体部分重量较大，靠曲柄连杆机构受力也是不行的。为了解决如上问题，我们设计了一种锁死机构，无论履带处于何种状态，都是由锁死机构负责支撑受力。这就大大保证了履带部分的可靠性与稳定性。

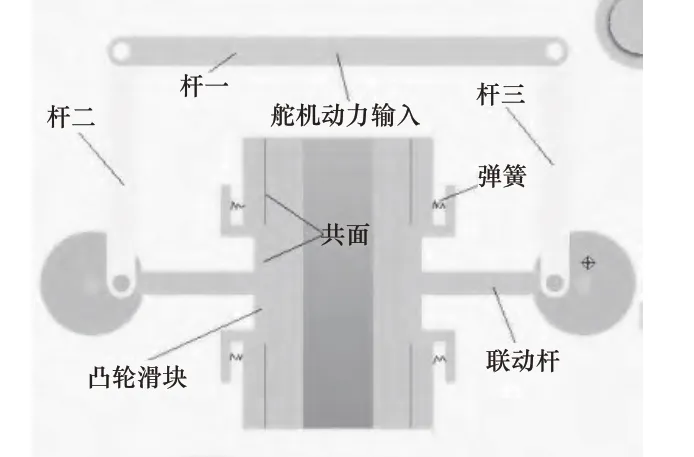
图7 锁死机构（滑块缩回）

滑道的左右两端各设置了一个凸轮滑块，当履带处于闲置状态时，凸轮滑块处于伸出状态，将支撑架滑块支撑起来，承受履带部分的重力；当履带向工作状态过渡时，凸轮滑块缩回，使其与滑道平面共面，紧接着曲柄滑块的舵机转动，将履带放下，滑块达到下极限行程位置时，舵机停止转动；凸轮滑块再次伸出，这样就可以讲支撑架滑块固定在最低端，履带工作。当履带由工作状态向闲置状态转换时，与上述流程相反。同时参照图7和图8。

图8 滑块伸出状态

为了使控制凸轮滑块的伸出与缩回（往复直线运动），我们设计了一种凸轮机构。凸轮机构的特点为：可以将旋转运动，转换为往复的直线运动，同时凸轮可以承受较大的径向力。为了保证凸轮滑块的复位，我们将滑块的上下两端各设定了一个弹簧，这样也可以保证滑块上的联动杆可以紧贴凸轮。凸轮中心与联动杆轴线共线。

凸轮的元周线由三种圆弧组成。当凸轮滑块联动杆上的圆弧与凸轮大圆弧相切时，凸轮滑块被顶起伸出；当切点由大圆弧经小圆弧过渡到中型圆弧时，由于弹簧的弹力，使联动杆紧贴凸轮弧线，滑块慢慢回缩；当切点达到中型圆弧最低点时，滑块完全缩回，与滑道平面共面。这样就实现了凸轮滑块的伸出与缩回的转换。

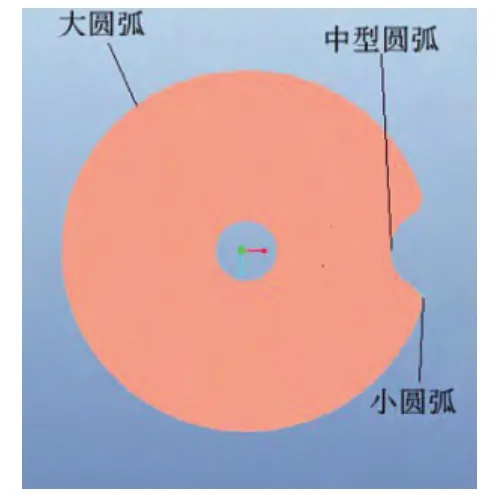
图9 凸轮周线布置

由于一个滑道系统对应着左右两个凸轮，为了节约成本，最理想的情形是，一个主动力输入可以使两个凸轮同时旋转。为了达到这一目的，我们设计了一种四连杆凸轮机构，其工作原理类似于四连杆，且构件初始时保持对称。

杆一的中心部分与舵机主轴相连，作为动力输入。杆一左右两端铰接着杆二与杆三，杆二与杆三的另一端分别与左右凸轮上的一点铰接。同时参照图9[3]。

当凸轮滑块处于缩回状态时，左右凸轮中心及其各自的铰接点与联动杆共线，此时，四连杆凸轮机构的形状为矩形；杆一的舵机旋转一个小角度时，带动杆一转动，杆一带动左右的杆二与杆三平动，从而带动左右的凸轮各自转动一定角度，再带动凸轮滑块伸出。这样在整体上就实现了对凸轮滑块的控制。同时参照图9和图10。

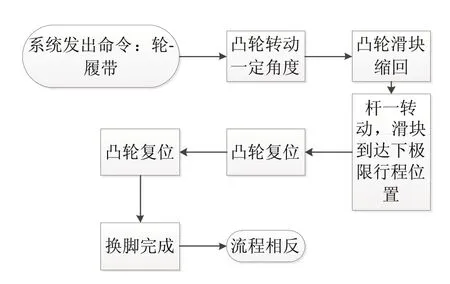
图10 摇臂式履轮转换机构工作流程图

2 机构特性

摇臂式履轮转换机构最关键的部位是支持车体上下移动的曲柄滑块机构。履带支撑架的升降由曲柄滑块机构控制，这种机构结构简单，稳定性好，噪音小。同时，支撑架为对称结构，可以保证履带工作的平稳性。起升降作用的曲柄滑块机构可抽象为图11所示。

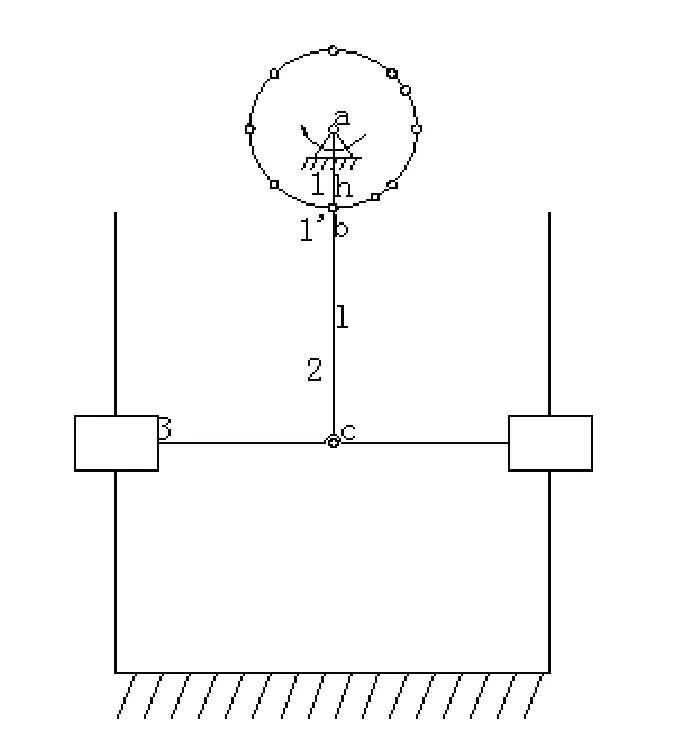
图11 曲柄滑块系统

2.1 机构的干涉约束

当支撑架上的滑块处于上极限行程位置时，曲柄与连杆重合，当滑块处于下极限行程位置时，曲柄与连杆共线，且这两种状态下的直线俊处于竖直位置，所以，有：

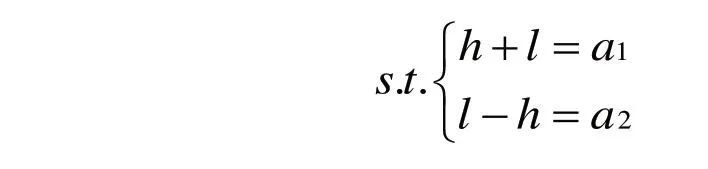
其中：l为连杆长度，h为曲柄长度，a1为支撑架上滑块处于下极限行程位置时距曲柄销钉的竖直距离，a2为滑块处于上极限行程位置时距曲柄销钉的竖直距离。a1，a2的大小均由机构布局人为设定[4]。

2.2 机构的速度加速度分析计算

已知：经过舵机驱动杆1一恒角速度旋转，做周期性运动。取b点经过的点1’，2’，3’，4’，5’，6’进行分析。用矢量方程图解法求解：

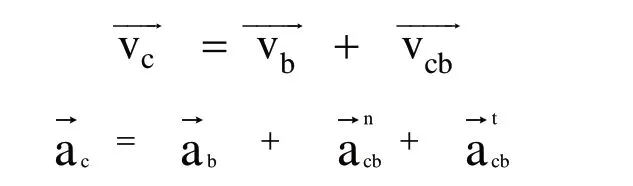
图12 速度矢量图

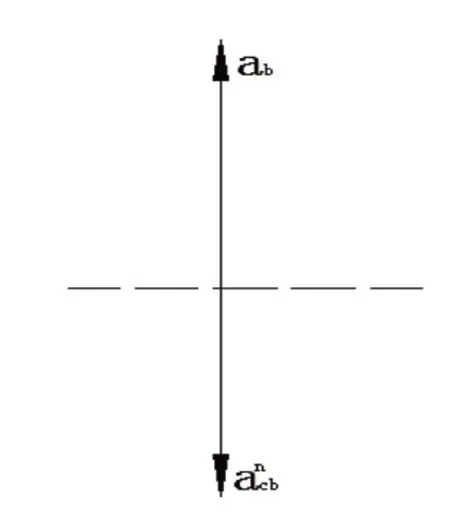
图13 加速度矢量图

以此类推，可得图中各点的速度与加速度。

3 整机摇臂式履轮转换曲柄滑块机构的运动仿真

完成了摇臂式履轮转换机构的整机在Pro/E中的建模与装配后，将建立在虚拟样机中的曲柄滑块机构系统另存为Parasolid格式导入ADAMS进行运动学仿真[6]。在ADAMS中，完成含有运动学特性的虚拟样机仿真环境的设置，仿真时间的确定，约束关系的确立，使机构能够进行联动，在该环境下进行齿轮传动机构的运动学仿真。其建模后添加约束效果如图14所示。

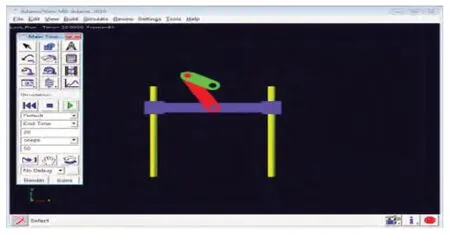
图14 系统动力建模

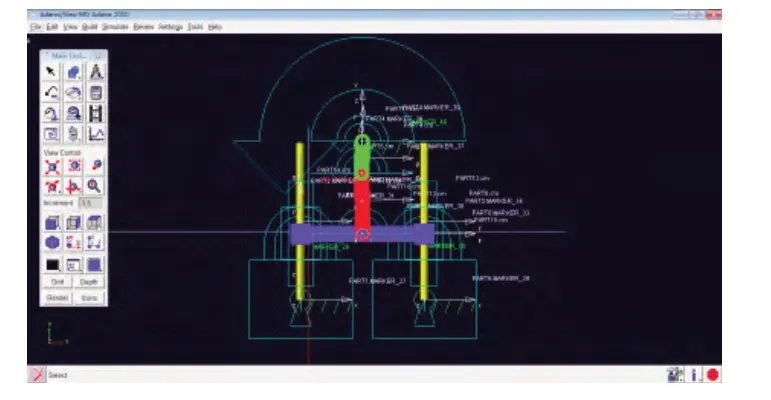
图15 系统添加约束

图16 摇臂式履轮转换输出速度

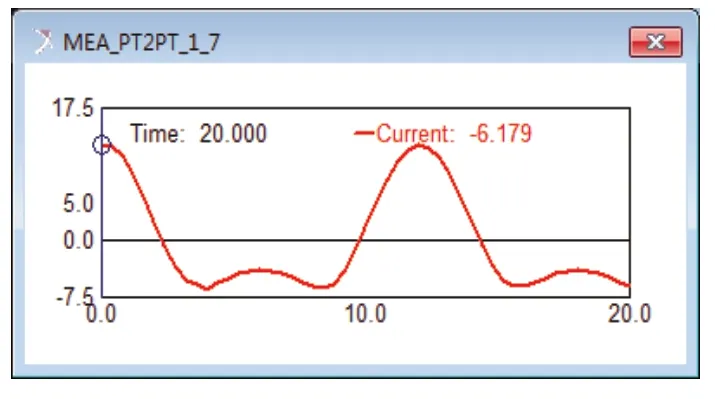
图17 摇臂式履轮转换输出加速度

4 结束语

整个摇臂式铝轮转换机构的设计首先提出了一种换脚机构，进而对其建立初步模型，细化其工作过程，然后利用同一构件上的两点间的运动矢量方程做机构的速度及其加速度的图解分析。最后将建立的机构用ADAMS软件进行仿真分析，由结果可得出此机构具有可行性，运行平稳，结构紧凑简单，能够支持较大范围的扭矩，能很好地满足工作需要，为作为机器人各种作业搭载平台的行走机构的设计提供了参考。

[1] 蔡自兴.共创中国机器人学的合作发展新路[J].机器人技术与应用,2012,01:8-10.

[2] 陈德明.四足仿生机器人运动控制系统的设计与实现[D].西北工业大学,2007.

[3] 景仁坤.基于Pro/Engineer的三维参数化设计研究与开发[D].武汉理工大学,2005.

[4] 黄小龙.虚拟样机技术在“机械原理课程设计”教学中的应用[J].中国电力教育,2013,04:102-103+109.

[5] 朱玉.Pro/E和ADAMS在《机械原理课程设计》教学中的应用[J].江苏教育学院学报(自然科学版),2006,04:112-114.

[6] 汪奇谋,李华,姚进.基于ADAMS的变速箱传动系统的动力学仿真[J].机械传动,2013,06:75-77.