机器手臂轨迹规划

王凯凯，万 衡

WANG Kai-kai, WAN Heng

（上海应用技术学院 电气与电子工程学院，上海 201413）

0 引言

机器人轨迹规划算法是目前机器人领域的研究热点，其中主流的五次多项式插值法可以满足起始点和结束点的速度与加速度为零，B样条函数插值法的局部性特点较好，但其各自也存在一定缺陷，限制了使用范围。本文给出了一种起始点与目标点采用五次多项式，中间点采用三次B样条插值法的混合算法——“五－B－五”轨迹规划算法，在实际应用中取得了较好的效果。

1 当前机器人轨迹规划的算法及其问题

1.1 五次多项式插值法

五次多项式插值法是机器人轨迹规划中应用比较广泛的一种算法[1]。假定对机器人的运动轨迹要求严格，约束条件过高，通常采用阶数比较高的五次多项式对运动轨迹进行规划。五次多项式插值法相对比较简单，运算量不大，该算法的起始点与目标点的速度与加速度曲线可以同时为零，且整段角位移曲线平滑，速度与加速度曲线连续。但该算法关节位移变化大，任意关节点参数的变化都将对整条曲线产生非常大的影响，使得在分段的间隔点处不能保证加速度的连续性，使得五次多项式插值法的应用得到了一些限制。五次多项式可设为：

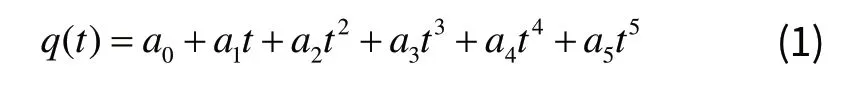
1.2 三次B样条函数插值法

B样条方法是Gordon、Riesenfeld等在1972年提出的[1]。B样条函数定义如下：

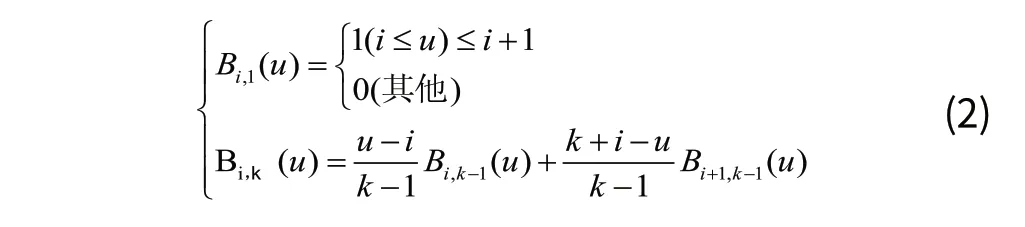
其中k>1；i=0，1，…，n-k；u为系数。

由于B样条曲线插值法对中间点关节角、关节角速度、关节角加速度曲线都是连续的，更主要的是B样条曲线具有分段处理的优点，各段仅由相邻的4个控制点确定，因此，变动特性多边形的某个顶点，只会影响与该顶点有关的相邻4段曲线，其他地方的曲线不会引起变化。但是起始点与目标点的速度与加速度曲线不能同时为零这一不足之处，会使机器手臂在起始点与目标点位置发生速度或加速度发生突变，必将引起机器人启动或者停止时的手部抖动，影响机器人工作的平稳性。

综上所述，这二种算法在各自领域应用都存在一些不足，因此为了解决这些不足之处，本文给出了一种新的算法。

2 五—B—五算法

通常情况下服务机器人对机器手臂的要求较高，约束条件比较多，如起始点与目标点的位置、速度与加速度，这样就需要满足六个约束条件。假如把五次多项式看做关节角值的时间函数，则五次多项式的一阶导数为关节角速度的时间函数，二阶导数为关节角加速度的时间函数，根据下式：

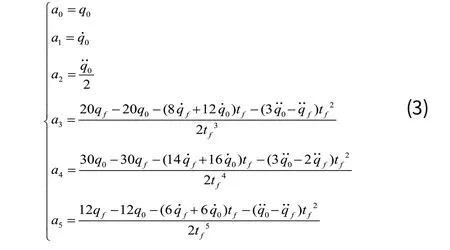
求得五次多项式函数曲线。其中 q0、 qf分别代表起始点与目标点关节角值，分别代表起始点与目标点关节角速度，分别代表起始点与目标点关节角加速度[2]。

假设机器手臂在关节空间中有一组型值点(任意时刻的关节角)P1,P2,…,Pm根据边界条件和连续条件可以求出m+2个控制点V0,V1,…,Vm+1任意的两个相邻的型值点可以用一条B样条曲线连接起来，这样整条轨迹曲线就由m-1 条B 样条曲线组合而成，第i 段曲线可以由四个控制点来控制[3,4]。

设四阶三次B样条函数表达式为：

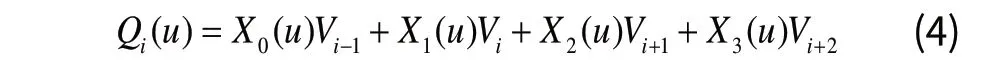
其中u(0 ≤ u ≤1)为参数；Qi(u)为第i段B样条曲线上的点；Xi(u)为参数多项式；V为控制点。根据文献[5,6]可得：

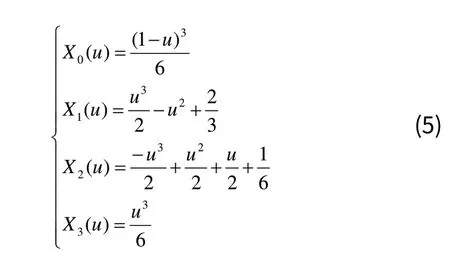
从而可得第i段B样条曲线为：

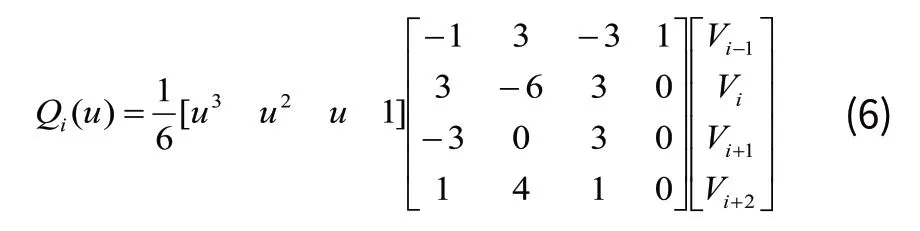
其中i=1，2，…，m；0≤u≤ 1；当u取遍0～1的所有数值时，即可求得一段完整的B样条曲线。由于选择的边界条件的限制，使速度曲线与加速度曲线的初始点与目标点必然不能同时为零。为了求解式(6)，我们采用边界条件选择为加速度曲线的起始点与目标点为零，即用为解控制点的边界条件。根据式(7)就可以求出完整的第i段B样条曲线。

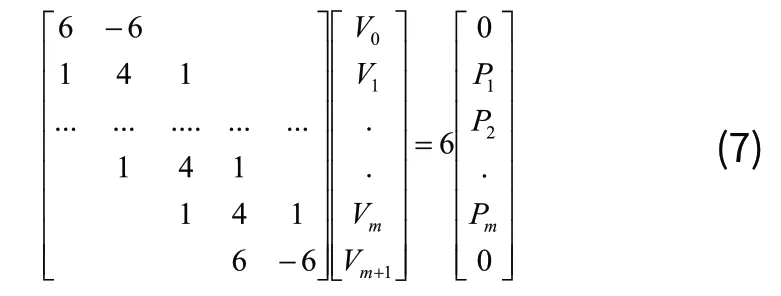
式(6)中u为未知参数，其从0～1遍历取值就可以得到第i段的B样条曲线，其中t(u)与q(u)分别表示该段曲线的横纵坐标。要绘制速度曲线和加速度曲线必须知道B样条的一阶导数和二阶导数，令一阶导数为二阶导数为则：

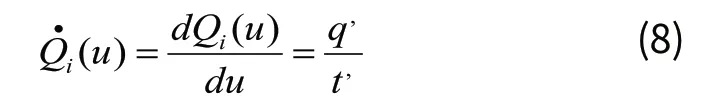
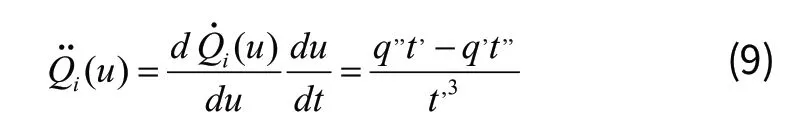
起始段与中间段及目标段的连接尤为重要，处理好可以保证整条曲线的连续平稳，处理不好则整个曲线则没有价值，达不到预期目标。在速度曲线中，起始段的结束速度V2必须与中间段的初始速度相同，终止段的初始速度V4必须与中间段的结束速度相同。在加速度曲线中，起始段的结束速度A2必须与中间段的初始速度相同，结束段的起始速度A4必须与中间段的结束速度相同，否则曲线不连续。

连接点的各参数设置如下：在关节角速度曲线中，起始段五次多项式曲线的起始速度取V1=0，结束速度取中间段B样条曲线开始时刻t1的速度V2，终止段五次多项式曲线的终止速度取V3=0，起始速度取中间段B样条函数曲线的结束点时刻t2速度V4。在关节角加速度曲线中，起始段五次多项式曲线的起始加速度取A1=0，结束加速度取中间段B样条的开始点加速度V2，终止段五次多项式曲线的终止加速度取A3=0，起始速度取中间段B样条函数曲线的结束点加速度A4。

具体算法如下：

1）输入起始点X、中间点Y1...Yi（i为整数）与目标点Z；

2 ）识别开始段X-Y1、中间段Y1-Yi和目标段Yi-Z；

3）计算出V1、V2、V3、V4、A1、A2、A3、A4；

4）判断若为起始点，连接起始点X与中间点Y1，调用公式(4)和公式(1)；

5）连接Y1于Y2，Y2与Y3，Yi-1与Yi，每段分别调用公式(6)；

6）连接Yi与目标点Z，调用公式(4)和公式(1)；

7）结束。

五—B—五算法结构图如图1所示。

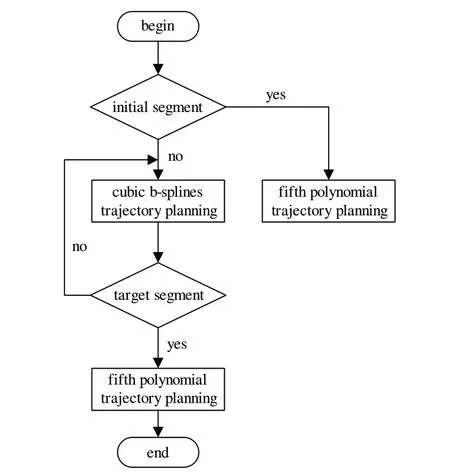
图1 五—B—五算法结构图

3 仿真验证

本文选取机器人其中一个关节为例来验证算法的可行性与稳定性，假设关节起始点x(0，-20)，中间点为y1(5，0)、y2(10，20)、y3(15，-30)、y4(20，50)，目标点为z(25，90)，根据上述所述可得到V1=0、V2=9.6667、V3=23.6667、V4=0，A1=A2=A3=A4=0。利用MATLAB编程[8,9]可得到下面的仿真图2、图3、图4。

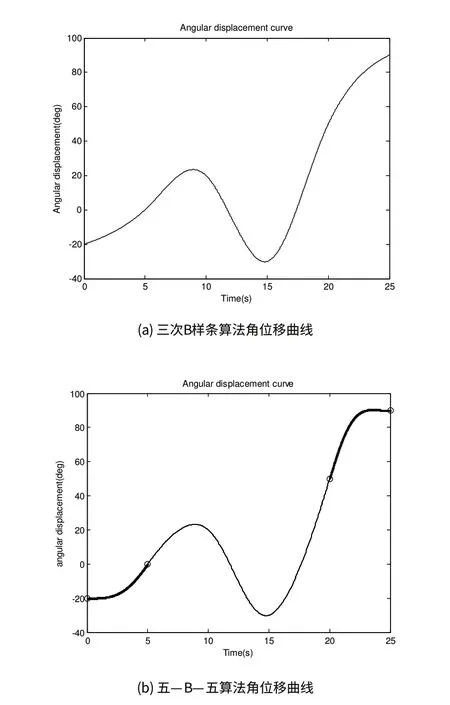
图2 角位移曲线

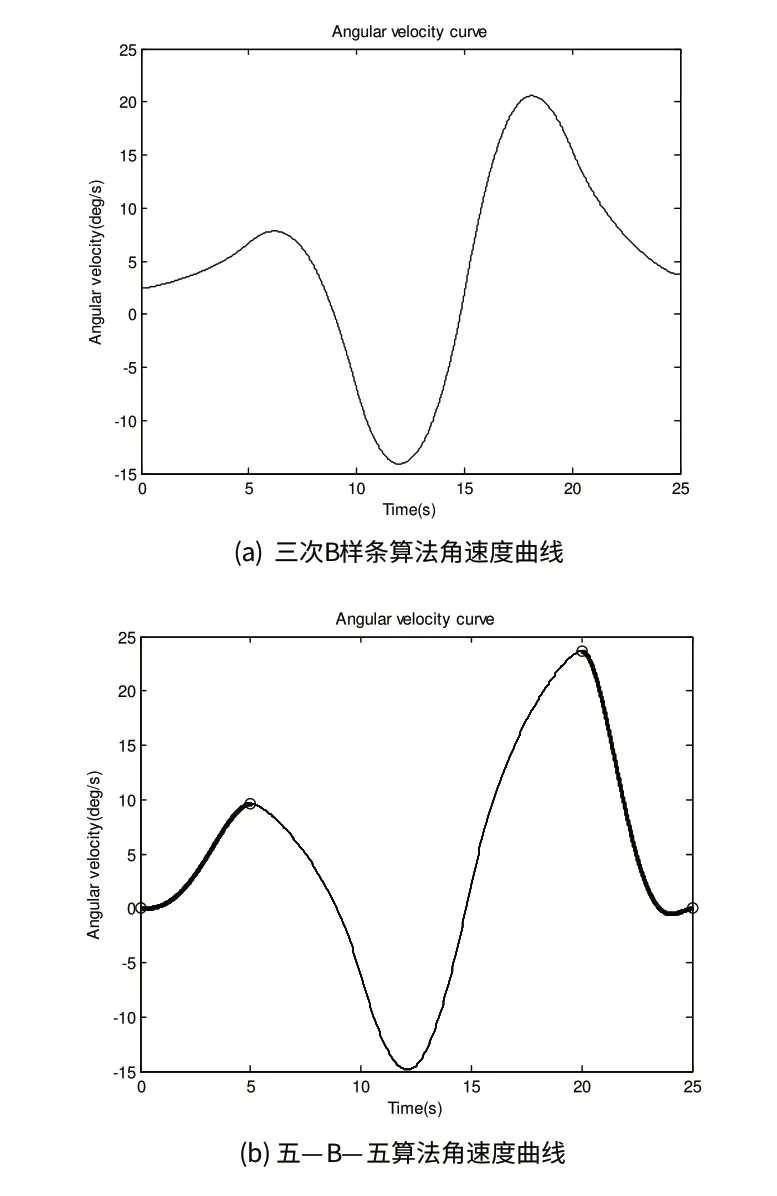
图3 关节角速度曲线

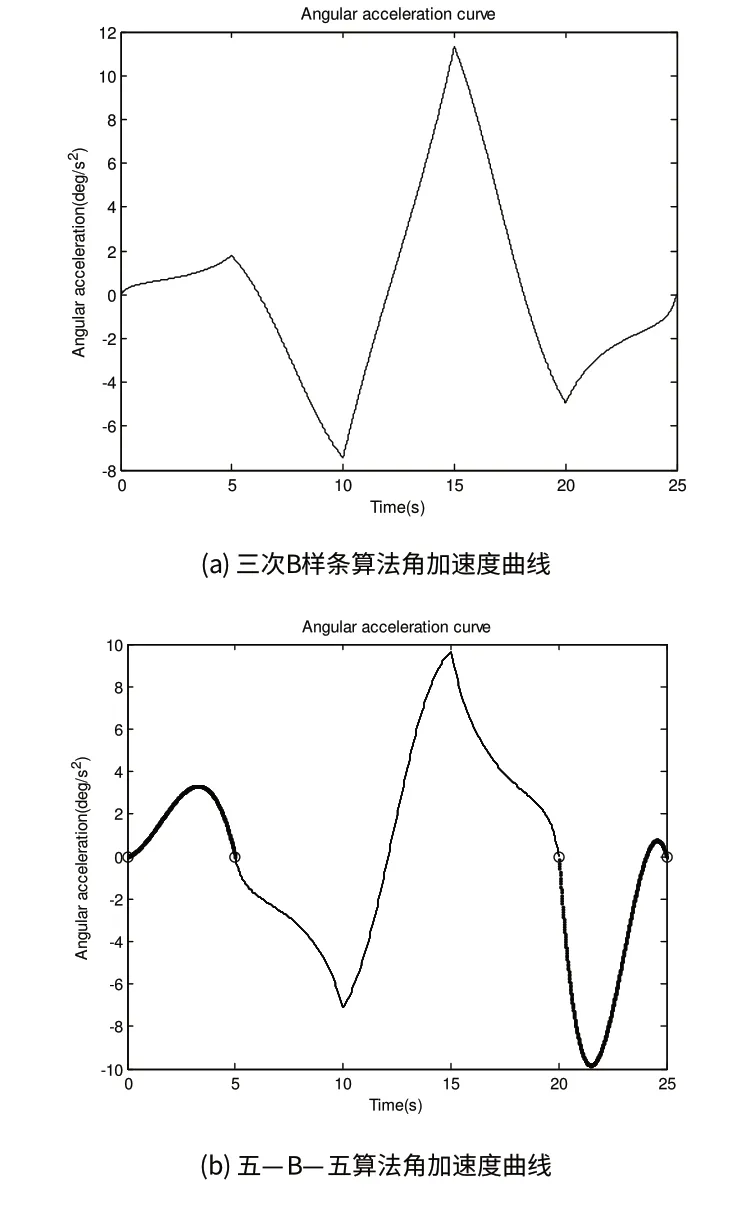
图4 关节角角加速度曲线

图2 (a)为三次B样条角位移曲线，图2(b)为五—B—五算法角位移曲线由图2(a)可以看出，机器人该关节角位移从起始点-20°开始，在第5秒达到第一个中间点0°，这段曲线为起始段，采用五次多项式插值法；在第10秒达到第二个中间点20°，在第15秒达到第三个中间点-30°，在第20秒达到第四个中间点50°，这三段曲线称为中间段，采用三次B样条曲线插值法；在第25秒达到目标点90°，这段曲线称为结束段，采用五次多项式插值法。整段曲线平滑、连续，变化平缓，不存在跳变，很好的达到预期的效果。

图3(a)与4(a)分别为三次B样条曲线速度与加速度曲线，图3(b)、4(b)分别为五—B—五算法速度与加速度曲线。由图3(a)与4(a)可以看出单独的三次B样条曲线的起始速度与起始加速度不同时为零，而由3(b)、4(b)可以看出，机器人该关节角速度曲线、加速度曲线连续，变化平缓，不存在跳变，且在起始点

与目标点的速度、加速度均为0，算法得到了很好的改善。

综上所述，该机器人关节的角位移曲线平滑连续、角速度和角加速度曲线连续，说明该关节在工作过程中运行平稳，不会产生较大的震荡。

4 结束语

本文针对当前一些机器手臂轨迹规划算法存在的不足，结合以往算法的优点，给出了一种“五—B—五”轨迹规划算法，该算法的角位移曲线连续，角速度曲线和角加速度曲线的起始点和结束点的速度和加速度都为零且连续，保证了机器人在运行过程中没有剧烈的抖动，延长了机器人的寿命。另外该算法的中间曲线部分采用四个控制点控制一段曲线的生成，在型值点发生意外变化时只能改变该小段的曲线变化，减少了误差。最后通过MATLAB对该轨迹规划算法仿真，取得了预期目标，为以后的机器人轨迹规划研究提供了很好的参考价值。

[1] 孙秀萍.机器人手臂轨迹规划的研究[J].内蒙古师范大学学报(自然科学汉文版),2009,38(2):174-177.

[2] A. Oasparettot ,V.Zanotto. A. new method for smooth trajectory planning of robot manipulators[J].Mechanism and Machine Theory,2007,42:455-471.

[3] 石忠,王永智,胡庆雷.基于多项式插值的自由漂浮空间机器人轨迹规划粒子群优化算法[J].四川宇航学报,2011,32(7):1516-1521.

[4] Jeng-Yih Chiou Robot Control System Based on Distributed Embedded Systems[J].Second International Conference on Innovative Computing,Information and Control(ICICIC 2007),2007:266-269.

[5] 王幼民,徐蔚鸿.机器人连续控制中B样条轨迹优化[J].机械设计.2000,10(10):33-36.

[6] Tan Guanzheng,Wang Yuechao. theoretical and experimental research on time-optimal trajectory planning and control of industrial robots[J].Control theory &Applications,2003(2):185-192.

[7] Lin Dingding,Liu Li,Zhao Jiandong,et al.ZMP-CoP Testing and Research of Biped Walking Robot[J].Robot,2004,26(4):368-379.

[8] 李双双.工业机器人建模、运动仿真与轨迹优化[D].内蒙古大学,2012.

[9] 王永龙,张兆忠,张桂红.MATLAB语言基础与应用[M].北京:电子工业出版社,2010.