基于力状态映射法的航天器非线性铰链参数辨识

吴爽，赵寿根，吴大方，罗敏

(1.北京航空航天大学航空科学与工程学院，北京100191;2.中国空间技术研究院总体设计部，北京100080)

由于航天器载荷舱内空间的限制，航天器中的某些重要组件在发射前需要折叠放置，因此需要使用可转动的铰链连接结构来实现折叠组合构件的在轨展开。航天器上的铰链结构形状复杂，在外界载荷作用下，其内部零件间会产生碰撞及摩擦，使其结构的刚度和阻尼表现出较强的非线性特点，这些非线性动力学特点使得铰链动力学参数的确定及其建模变得复杂且困难。航天器伸展机构的非线性主要来源于铰链结构的非线性刚度和非线性阻尼［1］，因此确定铰链结构的上述非线性动力学参数对建立航天器伸展机构的动力学模型非常重要。

国内外已有许多学者对铰链的动力学特性进行了研究，以确定其动力学参数。Ren等［2］将铰链与铰链组合体的动态特性的区别假设为铰链的影响，从它们结构的频率响应函数中提取铰链的参数。Wang［3］等根据测量得到的铰链频响函数估计了所有未测得的频响函数，并辨识了组合结构中铰链的线性动力学特性。以上文献仅考虑了铰链的线性特性，忽略了非线性因素对铰链动力学特性的影响，因此依据其方法获得的铰链模型与实际结构间会有一定的误差。王巍等［4］将航天器上的间隙铰链简化为由非线性弹簧组约束的非线性摆，并基于接触理论建立了此类铰链的分析模型。Boswald等［5］提出了一种应用频率响应残差辨识非线性铰链参数的方法。系统辨识是获得复杂结构动力学参数及模型的重要方法。目前，已有大量的基于时域或频域的非线性动力学系统辨识方法［6－8］，其中，由Crawley［9－10］提出的力状态映射法是一种重要的基于时域的非线性系统辨识方法，该方法将结构的非线性回复力表示为位移和速度三维空间上的单值曲面，其形状反映了结构的各种线性和非线性特性。随后，Kim等［11］提出了基于频域的力状态映射法。Masters等［12］将力状态映射法应用于多自由度框架结构的参数辨识。Meskell［13］等将力状态映射法应用于流体弹性系统，辨识了系统的线性和非线性刚度和阻尼参数。Namdeo等［14］应用再生核粒子法和克里金法对力状态映射图进行拟合，此方法适用于多自由度非光滑非线性系统。迄今为止，虽然已有学者对非线性铰链结构的动力学参数进行了辨识［5，15－16］，但仅研究并获得了铰链结构的部分非线性参数，对实际的航天器非线性铰链结构进行较为全面的动力学参数辨识和建模的研究还未见报道。

本文应用力状态映射法对实际航天器太阳翼根部铰链和板间铰链结构进行了非线性动力学参数辨识。针对根部铰链和板间铰链结构的受力特点设计试验测试方案，同时建立航天器复杂非线性铰链结构的振动响应试验测试系统，以获得铰链结构在不同频率及激振力下的力与振动响应之间的关系。采用力状态映射法对试验中的2种铰链结构分别进行非线性动力学参数辨识，并根据辨识结果建立描述铰链结构非线性特性的动力学模型。

1 力状态映射法

对于某个非线性弹簧质量阻尼系统，系统的状态可以完全由其位移x和速度描述，系统的动力学模型可以表示为二阶非线性微分方程:

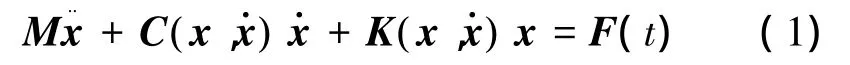
式中:广义阻尼C和广义刚度K是系统状态的函数。变换方程(1)中的各项可得

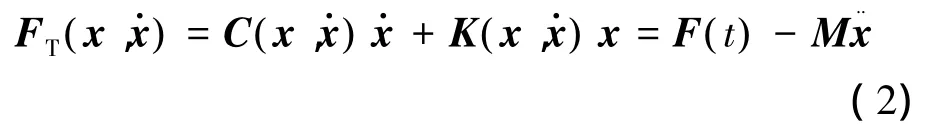
方程左侧的FT代表系统整体传递的力，它是系统瞬时状态的函数，称为传递力。

由方程(2)可做出描述系统传递力FT和对应状态(x)的三维曲面图，称为力状态图，它反映了系统的传递力FT、位移x和速度的关系，从图中可以提取系统的动力学参数。为了得到系统的力状态图，需要系统每一时间段的位移、速度、加速度和外力的值。图1为某一线性弹簧质量阻尼系统的力状态图，如图所示为一个倾斜的平面，其中传递力对位移的斜率即为系统的线性刚度k，对速度的斜率即为系统的线性阻尼c。

由以上原理可得应用力状态映射法辨识系统动力学参数的一般步骤为:1)选择一定的动态力施加于被辨识系统，同时测量被辨识系统在该力作用下的位移和速度等状态参量;2)对被辨识系统的动力学试验数据进行处理，并生成力状态图;3)从力状态图中提取被辨识系统的刚度和阻尼等动力学参数。

图1 线性弹簧质量阻尼系统的力状态图Fig.1 Force-state map of a linear spring mass damper system

2 铰链振动试验

2.1 试验对象的动力学特性分析

根部铰链和板间铰链是航天器上2种常用的连接结构，它们在航天器主体与太阳能帆板及板间起着重要的连接作用。航天器发射时，通过铰链连接的太阳能帆板折叠在运载工具内，入轨后展开成工作状态，根部铰链和板间铰链锁定。此时，由于太阳能帆板结构尺寸大、刚度低、柔性高，当受到外扰作用时便会产生强烈的振动，而铰链结构的非线性特点使其振动表现出较强的非线性特性。因此，分析此时铰链的动力学特性，确定其动力学参数是对系统实施振动控制的前提。本文主要研究处于锁定状态下的根部铰链和板间铰链的动力学特性。由于大多数太阳能帆板为矩形结构，其横向弯曲刚度较小，当受到外扰作用时，在一定条件下将表现为以横向一阶弯曲为主的弯曲振动，根部铰链和板间铰链主要承受弯矩，由此可将它们近似为单自由度的非线性结构。

2.2 根部铰链振动试验

由力状态映射法的原理可知，在辨识系统的动力学参数前，首先应得到系统在外力作用下的响应。本节针对根部铰链和板间铰链的结构及在系统中的受力特点，分别设计并实施了振动试验，以获得系统辨识所需的试验数据。

试验对象采用真实的某型号航天器太阳翼根部铰链，如图2所示。振动试验采用单频激励法。由于应用此铰链的太阳翼结构固有频率在3～6 Hz较为密集，因此分别采用3、4、5、6 Hz的单频信号作为激励信号对根部铰链实施振动试验。

试验中需要得到的物理量有根部铰链端部所受的动态力矩和其整体结构的动态弯曲角。为了便于试验中力的施加和状态参数的测量，在铰链的一端连接了一个附加梁，并将其另一端固定于试验台上，其整体系统的示意图和实物图如图3所示。试验采用电磁激振系统对铰链施加不同频率的激振力，它由功率放大器和激振器组成。激振器底端固定，通过一根直杆将其产生的激振力施加于附加梁端部的激振点。采用应变片和动态应变仪测量附加梁与铰链连接处的动态应变。采用激光非接触振动测试系统测量铰链端部的动态位移。图4显示了根部铰链应变和位移测点的布置情况。

图2 根部铰链结构图Fig.2 Structure diagram of the joint at the root of solar arrays

图3 根部铰链试验系统Fig.3 The experimental system of the joint at the root of solar arrays

试验实施时，在一定的控制信号下，激振器产生相应频率的激振力，附加梁在激振力的作用下运动，并对下端连接的铰链施加以动态力矩。在一定的采样时间和采样频率下，通过应变片和动态应变仪可测量得到附加梁下端应变测点处的动态应变值，由此动态应变可计算出此处附加梁截面的动态弯矩，而此动态弯矩近似等于铰链上端部所受的动态力矩。通过激光非接触振动测试系统可测量得到铰链上、下端位移测点处的位移值，进而可计算出铰链在上述动态力矩作用下产生动态变形对应的动态弯曲角。通过数据采集与处理系统采集和记录以上动态应变和位移的时间历程曲线。

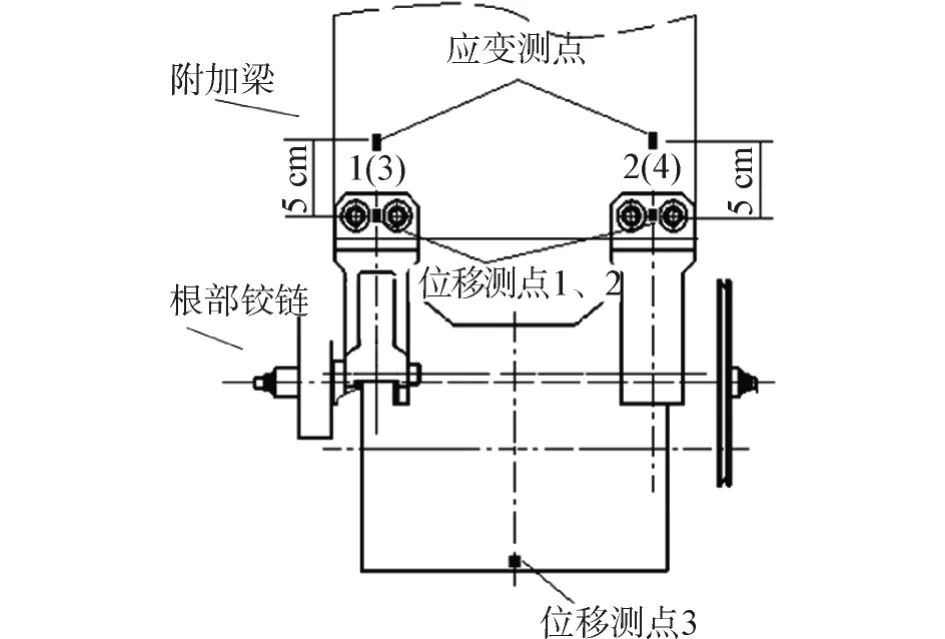
图4 根部铰链应变和位移测点布置图Fig.4 Strain and displacement measuring point arrangement of the joint at the root of solar arrays

2.3 板间铰链振动试验

试验对象采用真实的某型号航天器太阳翼板间铰链，如图5所示。振动试验同样采用单频激励法。需要得到的物理量有板间铰链端部所受的动态力矩和其整体结构的动态弯曲角。测试系统同样采用铰链与附加梁的连接形式，其整体系统的示意图和实物图如图6所示。试验设备和试验过程与根部铰链振动试验的相同。图7显示了板间铰链应变和位移测点的布置情况。

图5 板间铰链结构图Fig.5 Structure diagram of the joint between solar arrays

2.4 试验结果

由以上根部铰链和板间铰链的振动试验测得的数据可分别计算出它们在一定的激振力作用下的动态力矩和动态弯曲角。试验中，动态应变仪测量应变数据时采用全桥连接方式，因此，附加梁下端部的应变为

式中:ε1(t)、ε2(t)、ε3(t)、ε4(t)分别代表同一时刻测得的应变测点1、2、3、4处的应变值。

铰链上端部所受力矩近似等于附加梁下端部截面的弯矩，其计算公式为

式中:EIz为附加梁的弯曲刚度，h为附加梁的截面高度，β为应变片的位置修正系数。

铰链的弯曲角可由下式计算:

式中:d1(t)、d2(t)和d3(t)分别为同一时刻测得的位移测点1、2和3处的位移值，L为铰链的长度。

图6 板间铰链试验系统Fig.6 The experimental system of the joint between solar arrays

图7 板间铰链应变和位移测点布置图Fig.7 Strain and displacement measuring point arrangement of the joint between solar arrays

由于根部铰链和板间铰链的试验装置和测点布置相似，因此上述计算公式适用于2种铰链物理量的计算。图8为激振频率为3 Hz时，根部铰链和板间铰链的力矩－弯曲角的曲线。图8所示的力矩－弯曲角的迟滞回线充分体现了2种铰链结构中刚度和阻尼的复杂非线性特点。

图8 激振频率为3 Hz时根部铰链和板间铰链力矩－弯曲角曲线Fig.8 Moment vs.bending angle of the joint at the root of solar arrays and the joint between solar arrays driven at 3 Hz

3 铰链动力学参数辨识

3.1 基于力状态映射法的参数辨识

铰链的振动试验分别得到了2种铰链在4种激振频率下的力矩和对应的弯曲角，对弯曲角进行数值微分即可得到相应的角速度和角加速度值，从而得到传递力矩MT和对应的状态 θ，θ·( )。

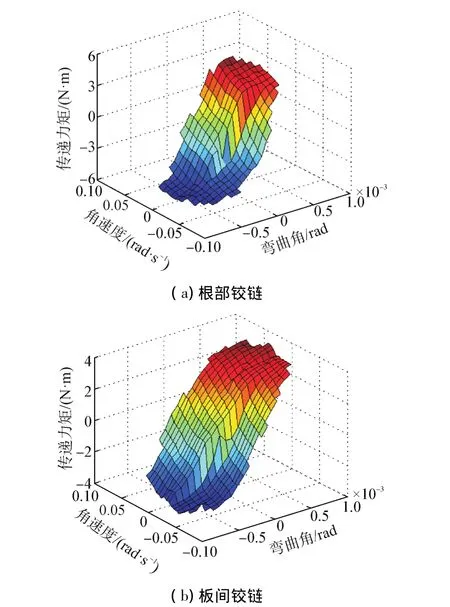
图9 激振频率为3 Hz时根部铰链和板间铰链的力状态图Fig.9 Force-state map of the joint at the root of solar arrays and the joint between solar arrays driven at 3 Hz

由于由试验数据得到的传递力矩在状态空间中成螺旋状旋转，无法直接做出传递力矩MT与对应的弯曲角θ，角速度θ·的三维曲面图，因此，可将弯曲角和角速度值的区间分别分成n个子区间，对其进行排列组合得到n×n个子区域，然后对每个区域对应的所有传递力矩取平均值M'T(i)，其中i=1，2，…，n，即可做出传递力矩M'T(i)与对应状态区域的三维力状态曲面图。图9显示激振频率为3 Hz时根部铰链和板间铰链的力状态图。

由图9可以看出，2种铰链的力状态图形状相近，并且都表现了高度的非线性特点。2种铰链的传递力矩在角速度为零时发生阶跃，此现象表明它们的结构中存在着库伦摩擦力矩。对于同一角速度，它们的传递力矩随弯曲角呈非线性变化，这表明它们的结构中存在着非线性弹性力，可用线性弹簧、二次和三次非线性弹簧共同描述。此外，图9还显示了它们的传递力矩与角速度呈线性关系，这表明2种铰链结构中还存在着线性粘性阻尼。基于以上分析可得2种铰链的传递力矩表达式:

其中，方程左侧为传递力矩;右侧第1项为线性阻尼力矩，c1为线性阻尼系数;第2、3和4项为非线性弹性力矩，k1为线性弹簧刚度系数，k2和k3为非线性弹簧刚度系数;第5项为库伦摩擦力矩，MF为库伦摩擦因数。对式(6)进行变换可得到2种铰链的动力学方程:

为了确定2种铰链的各动力学参数值，应用最小二乘法分别对图9所示的根部铰链和板间铰链的力状态图进行曲面拟合。拟合时以弯曲角和角速度为自变量，采用二元三次多项式作为拟合函数，拟合后的均方根误差分别为0.787 N·m和0.494 N·m，所得多项式的各项系数即分别为2种铰链的动力学参数。基于以上步骤，分别对2种铰链在激振频率为4、5、6 Hz时的试验数据进行参数辨识，表1和表2列出了2种铰链的参数辨识结果。

表1 根部铰链的参数辨识结果Table 1 Identified parameters of the joint at the root of solar arrays

表2 板间铰链的参数辨识结果Table 2 Identified parameters of the joint between solar arrays

3.2 结果与分析

通过对2种铰链力状态图的分析得到根部铰链和板间铰链结构中的线性和非线性动力学特性主要有线性弹簧刚度、线性粘性阻尼、库伦摩擦、二次和三次弹簧刚度。这些动力学特性体现了2种铰链结构所具有的复杂动力学特点。其中，库伦摩擦是铰链的非线性阻尼，是由铰链结构中零件间的接触和碰撞产生的。二次和三次弹簧刚度是铰链的非线性刚度，是由铰链中的弹簧结构产生的。这些非线性结构特点是造成铰链非线性行为的主要原因。

由表1和表2中2种铰链的参数辨识结果可以看出，在所选频率范围内，各参数的标准差均较小，且各参数值随频率变化无明显的规律，这表明辨识参数基本不受频率变化的影响。因此，可取其平均值代入式(7)，即可获得2种铰链的动力学方程。

另外，2种铰链的参数辨识结果还显示了根部铰链的各参数值都远大于板间铰链的各参数值。例如，板间铰链的二次弹簧刚度系数的平均值为－1.927×105(N·m)/rad2，根部铰链的相应参数值为 －6.273×105(N·m)/rad2，是板间铰链的326%;板间铰链的三次弹簧刚度系数的平均值为－2.684×109(N·m)/rad3，根部铰链的相应参数值为 －7.425×109(N·m)/rad3，是板间铰链的277%。这表明，在航天器系统设计时需要特别重视根部铰链对整体系统动力学特性的影响。

通过振动响应试验，采用力状态映射法辨识了2种铰链结构中的多种线性及非线性动力学参数，并初步建立了它们的动力学模型。同以往文献中对铰链的研究相比，本文采用了真实的具有复杂非线性动力学特点的航天器铰链结构，分析并辨识了其结构中的多种线性和非线性动力学特性，并基于此建立了描述其结构非线性特点的动力学方程，为建立精确的航天器系统模型及进一步实施主动控制提供了重要的理论参考。本文基于根部铰链和板间铰链结构在航天器系统中的受力特点，将它们近似为单自由度的非线性结构，而对于航天器的其他连接结构，可根据其受力特点，将其模型推广至多自由度，应用基于多自由度的力状态映射法对其进行参数辨识。

4 结束语

本文针对航天器伸展机构中铰链的非线性动力学特点，利用由试验获得的真实铰链的动力学试验数据，采用力状态映射法辨识了太阳翼根部铰链和板间铰链结构中的多种线性及非线性动力学参数，并在此基础上建立了铰链的非线性动力学模型。由于动力学试验采用了真实的航天器复杂非线性铰链结构，且运用了非线性系统辨识方法对试验数据进行多种动力学参数的辨识，因此所建模型能够反映真实铰链的非线性刚度、摩擦及阻尼特性。本文应用力状态映射法辨识非线性铰链动力学参数的方法适用于航天器中其他连接结构的参数辨识，其辨识结果也为进一步分析航天器伸展机构的动力学特性提供了理论参考。

［1］CRAWLEY E F.Nonlinear characteristics of joints as elements of multi－body dynamic systems.N89－24668［R］.Workshop on Computational Methods for Structural Mechanics and Dynamics.Hampton:NASA Langley Research Center，1985.

［2］REN Y，BEARDS C F.Identification of‘effective’linear joints using coupling and joint identification techniques［J］.Journal of Vibration and Acoustics，1998，120(2):331－338.

［3］WANG Mian，WANG Dong，ZHENG Gangtie.Joint dynamic properties identification with partially measured frequency response function［J］.Mechanical Systems and Signal Processing，2012，27:499－512.

［4］王巍，孙京，于登云，等.基于接触理论的一类带锁定机构的间隙铰链分析模型研究［J］.宇航学报，2004，25 (1):1－4，12.

WANG Wei，SUN Jing，YU Dengyun，et al.Analytical model for complex joint with latch mechanism of space structure［J］.Journal of Astronautics，2004，25(1):1－4，12.

［5］BÖSWALD M，LINK M.Identification of non－linear joint parameters by using frequency response residuals［C］//International Conference on Noise Vibration Engineering.Kassel，2004:3121－3140.

［6］KERSCHEN G，WORDEN K，VAKAKIS A F，et al.Past，present and future of nonlinear system identification in structural dynamics［J］.Mechanical Systems and Signal Processing，2006，20(3):505－592.

［7］SUBUDHI B，JENA D.A differential evolution based neural network approach to nonlinear system identification［J］.Applied Soft Computing，2011，11(1):861－871.

［8］LEE Y S，TSAKIRTZIS S，VAKAKIS A F，et al.A timedomain nonlinear system identification method based on multiscale dynamic partitions［J］.Meccanica，2011，46(4): 625－649.

［9］CRAWLEY E F，AUBERT A C.Identification of nonlinear structural elements by force－state mapping［J］.AIAA Journal，1986，24(1):155－162.

［10］CRAWLEY E F，O＇DONNELL K J.Force－state mapping identificationof nonlinear joints［J］.AIAA Journal，1987，25(7):1003－1010.

［11］KIM W J，PARK Y S.Non－linear joint parameter identification by applying the force－state mapping technique in the frequency domain［J］.Mechanical Systems and Signal Processing，1994，8(5):519－529.

［12］MASTERS B P，CRAWLEY E F.Multiple degree－of－freedom force－state component identification［J］.AIAA Journal，1994，32(11):2276－2285.

［13］MESKELL C，FITZPATRICK J A，RICE H J.Application of force－state mapping to a non－linear fluid－elastic system［J］.Mechanical Systems and Signal Processing，2001，15 (1):75－85.

［14］NAMDEO V，MANOHAR C S.Force state maps using reproducing kernel particle method and Kriging based functional representations［J］.Computer Modeling in Engineering and Sciences，2009，1050(1):1－37.

［15］IRANZAD M，AHMADIAN H.Identification of nonlinear bolted lap joint models［J］.Computers＆ Structures，2012，96/97:1－8.

［16］MEHRPOUYA M，GRAHAM E，PARK S S.FRF based joint dynamics modeling and identification［J］.Mechanical Systems and Signal Processing，2013，39(1/2):265－279.