柴油机BP-PID调速器性能改善研究
胡松,王贺春,杨洪衬,王银燕
(1.哈尔滨工程大学动力与能源学院,黑龙江哈尔滨150001;2.哈尔滨工程大学材料科学与化学工程学院,黑龙江哈尔滨150001)
相继增压、可调二级增压、VGT技术可增加柴油机的功率密度,改善瞬态性能,减小油耗及排放[1-2];EGR技术和相继增压、可调二级增压或VGT联合运用已成为降低NOx同时兼顾Soot排放的主要措施[2-3]。然而,采用这些技术的柴油机在运行过程中进排气压力会产生较大波动,使柴油机运行不稳定,调速性能变差。目前最常用的柴油机电子调速系统仍是PID调速,柴油机存在非线性和时变性,对于不同的运行工况、不同工作环境,最佳的PID控制参数会有较大变化。随着调速目标和要求的精确化,以及柴油机系统中各种非线性和时变因素的影响,人工调试、整定PID参数费时费力,并且存在着控制参数一经确定,不能在线调整的问题。人工神经网络具有自学习、自组织、自适应以及很强的非线性函数逼近能力和容错能力,特别适用于非线性系统特性的研究[4]。误差反向传播(BP)神经网络是目前应用最广泛的神经网络之一[5-6]。为改进传统PID控制算法的不足,将经典增量式PID控制规律融合进神经元网络之中形成BP-PID控制器,可以使控制系统达到响应快、超调小、无静差的效果,根据控制效果进行在线学习和调整以实现PID参数自动调整,达到较好的控制性能[7]。PID调速器输入信号局限于目标值、实际值和偏差,而对于BP-PID控制器,由于BP神经网络的非线性逼近特性,和输出相关的信号均可以作为其输入信号。文献[7-8]将神经网络PID控制算法应用到柴油机调速上,分别进行了试验研究和半实物仿真研究,结果表明了该算法具有较好的调速性能。但是文献[7-8]中神经网络PID算法的输入信号选为目标值、实际值和偏差,而未加入更多和转速相关的信号。对于进排气压力会产生较大波动的柴油机,进排气压力的变化对柴油机转速的影响很大,为进一步提高其调速性能,本文以相继增压柴油机为例,除目标转速、实际转速、转速偏差3个输入信号之外,增加进排气压力作为输入信号,以研究加入进排气压力作为BP-PID调速器输入信号对相继增压切换过程调速性能的影响。
1 柴油机及增压系统仿真模型及验证
TBD234V12柴油机原机采用脉冲增压系统,冲程为140 mm,缸径为128 mm,压缩比为15∶1,额定功率为444 kW,额定转速为1 800 r/min,最高燃烧压力为15 MPa,在原增压系统基础上,改造成相继增压柴油机。
采用GT-power软件建立的TBD234V12柴油机及其相继增压系统仿真模型在1TC(一个增压器运行)和2TC(2个增压器运行)状态下稳态计算结果与试验数据对比如表1所示。由表1可以看出,仿真计算结果与试验数据误差除1TC状态下10%工况点的油耗误差为4.5%,其余均在3%之内。

表1 计算结果与试验数据对比Table 1 Comparison of the simulation and measured results
2 舍弃节油区问题
图1为TBD234V12柴油机分别在1TC和2TC状态下按螺旋桨特性稳定运行于各工况点时试验所得油耗值。n12为相继增压系统切入过程(由1TC切换至2TC)的设定转速,n21为相继增压系统切出过程(由2TC切换至1TC)的设定转速。由于n12和n21需有一定的差值,并且 n12>n21[9],因此会产生一个舍弃节油区,如图1中阴影区域所示。对于采用可调二级增压系统的柴油机,也会由于n12和n21的差值而产生一个类似的舍弃节油区。舍弃节油区面积随着设定转速之间差值的增大而增大,使柴油机经济性降低。而相继或可调二级增压切换过程中的转速波动大小直接决定切换设定转速之间差值的大小,因此,对于具有相继或可调二级增压系统的柴油机来说,减小切换过程转速波动显得尤为重要。

图1 TBD234V12柴油机分别在1TC和2TC状态下的油耗值Fig.1 Consumption values of TBD234V12 diesel engine in 1TC and 2TC condition,respectively
3 BP-PID调速器控制算法
采用MATLAB/Simulink搭建BP-PID调速器仿真模型,其控制算法包括增量式PID控制算法和BP神经网络控制算法。
3.1 经典增量式PID控制算法
增量式PID的输出只与当前和前2步的误差有关,能有效避免微量误差的累加对系统带来的影响,既可减小误动作,又可减少积分失控的可能。增量式PID的数学模型表示为
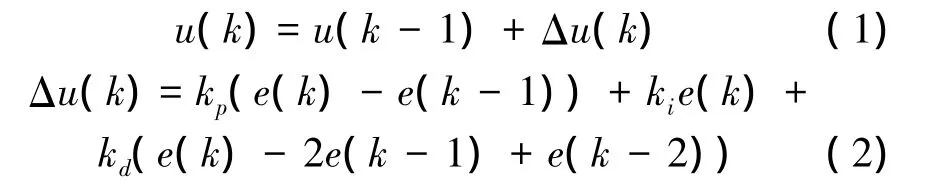
式中:u(k-1)、u(k)分别为第k-1和第k步调速器的输出,e(k-2)、e(k-1)、e(k)分别为第k-2、第k-1、第k步目标值与实际值之间的控制误差,kp、ki、kd分别为比例增益、积分增益、微分增益。
3.2 BP神经网络控制算法
BP神经网络可以包含不同数量的隐含层。在不限制隐含层节点数的情况下,具有1层隐含层就可以实现任意非线性映射,只有当学习不连续函数时,才有必要增至2层。柴油机调速系统属于连续系统,选取1层隐含层可以满足非线性映射需求,因此本文所用BP神经网络为3层结构。a为隐含层节点数,b为输入层节点数,c为输出层节点数。
网络输入层转换函数取为f(·),隐含层和输出层活化函数取为g(·)。f(·)和g(·)如下:

取性能指标函数为
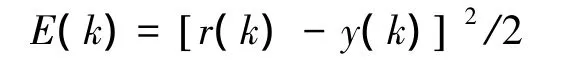
用BP学习算法来修正权系数,即按性能指标函数E(·)对加权系数的负梯度方向进行搜索调整,并附加使搜索快速收敛全局极小的惯性项:

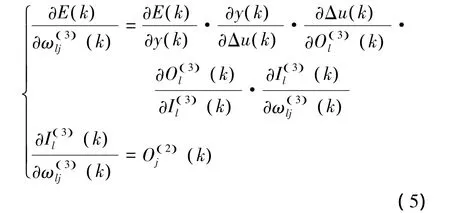
由于∂y(k)/∂Δu(k)未知,所以近似用符号函数sgn(∂y(k)/∂Δu(k))取代。
BP神经网络输出层权系数的学习算法为

同理可得隐含层的加权系数学习算法为

由于BP网络输入层的输入值通常量级不同,且变化范围较宽,会引起网络训练时间大大增加,甚至可能造成网络不能收敛。因此有必要对网络输入数据进行归一化处理,以使不同参量去量纲化,缩小数字差别,加快网络收敛。本文中对采样数据采用的归一化方法数学模型如下:

式中:A为调整参数。
由式(3)中输出层的活化函数g(·)可以看出,经g(·)映射后的输出值范围为(0,1)。而最佳的比例常数、积分常数和微分常数通常不局限于这一范围之内,并且数量级不同。因此需要对输出层进行反归一化,使比例常数、积分常数和微分常数满足调整要求。本文采用的反归一化方法数学模型如下:
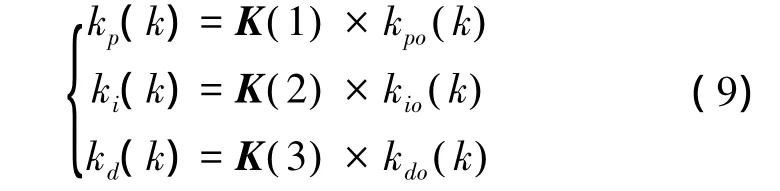
式中:K为反归一化矩阵,kpo、kio、kdo分别为K(1)、K(2)、K(3)经g(·)映射后的输出值。
对K取适当的矩阵,可以使kp、ki、kd在合适的范围内变动,以满足控制要求。
经神经网络优化调整得到的kp、ki、kd,代入式(1)和式(2),最终计算得到调速器输出喷油量。
3.3 BP-PID控制器输入信号及节点数的选取
由于BP神经网络可以实现任意非线性映射,并且能学习和存储大量的输入输出之间的映射关系,而无需事前揭示描述这种映射关系的数学方程[3,5],因此,和BP神经网络控制器输出相关的信号均可以作为其输入信号。但是,将相关性不大的信号作为BP神经网络的输入信号会增加控制器的计算量,并且减慢收敛速度,导致控制精度及响应速度降低、稳定时间延长[10]。对于柴油机调速器来说,通常输入信号选为目标转速、实际转速、转速偏差。进气压力和排气压力决定柴油机进气质量和泵功损失的大小,影响柴油燃烧效率和有效输出功率,进而影响柴油机转速。因此,进气压力和排气压力与柴油机转速有很大的相关性。在柴油机进排气压力不产生剧烈波动的情况下,由此所引起的转速波动较小,对柴油机调速性能影响不大。而对于具有相继增压系统、可调二级增压系统、VGT或者EGR系统的柴油机来说,在相继增压、可调二级增压切换过程中以及VGT喷嘴环、EGR阀开度变化过程中会引起发动机进排气压力较大波动,造成较大的转速波动。对于会产生进排气较大波动的柴油机,本文尝试把进排气压力也作为BP-PID调速器的输入,进一步改善柴油机的调速性能。
本文选取目标转速、实际转速、转速偏差为BPPID调速器的输入信号,建立传统BP-PID调速器仿真模型;选取目标转速、实际转速、转速偏差、进气总管压力、排气总管压力为BP-PID调速器的输入信号,建立改进BP-PID调速器仿真模型。
对于传统BP-PID调速器,输入信号个数为3,因此输入层节点数选为3;对于改进BP-PID调速器,输入信号个数为5,输入层节点数选为5。BP神经网络用来调整增量式PID的比例系数、积分系数和微分系数,因此输出层节点数选为3。
隐含层神经元节点数量根据下式确定[9]:
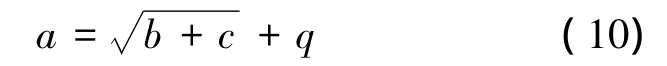
式中:q∈[1,10],为隐含层神经元节点数。
本文中传统BP-PID调速器,隐含层节点数选为5,采用3-5-3的三层网络结构;为避免由隐层节点数的变化所带来的影响,改进BP-PID调速器隐含层节点数仍选为5,采用5-5-3的三层网络结构。
4 切换过程仿真结果分析
所研究的柴油机用于船舶推进,扭矩和转速之间的关系符合螺旋桨特性。为对比增量式PID、传统BP-PID以及改进的BP-PID调速器在相继增压切换过程中的调速性能,本文中n12设定为1 428 r/min,n21设定为1 382 r/min,进行了相继增压切换过程仿真计算,计算结果如图2~7所示。
由图2可以看出,采用增量式PID算法的调速器时,在相继增压切入和切出过程中转速波动分别为37 r/min和38 r/min;采用传统BP-PID算法的调速器时,转速波动分别为31.5 r/min和29 r/min,和增量式 PID调速器相比,分别减小了 14.9%和23.7%;采用改进的BP-PID算法的调速器时转速波动分别为26 r/min和25 r/min,和增量式PID调速器相比,分别减小了29.7%和34.2%,和传统BPPID调速器相比,分别减小了17.5%和13.8%。而在相继增压系统不进行切换时,改进的BP-PID调速器和传统BP-PID调速器的调速性能差别很小,前者比后者超调转速减小0.5 r/min。

图2 3种调速算法的柴油机转速变化曲线Fig.2 Diesel engine speed curves using different control algorithms

图3 排气总管压力变化曲线图Fig.3 Pressure curve of exhaust pipe
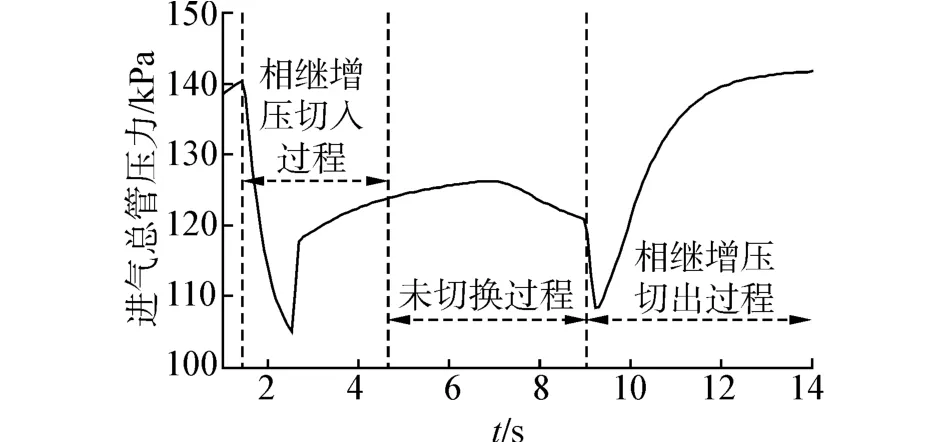
图4 进气总管压力变化曲线Fig.4 Pressure curve of inlet pipe
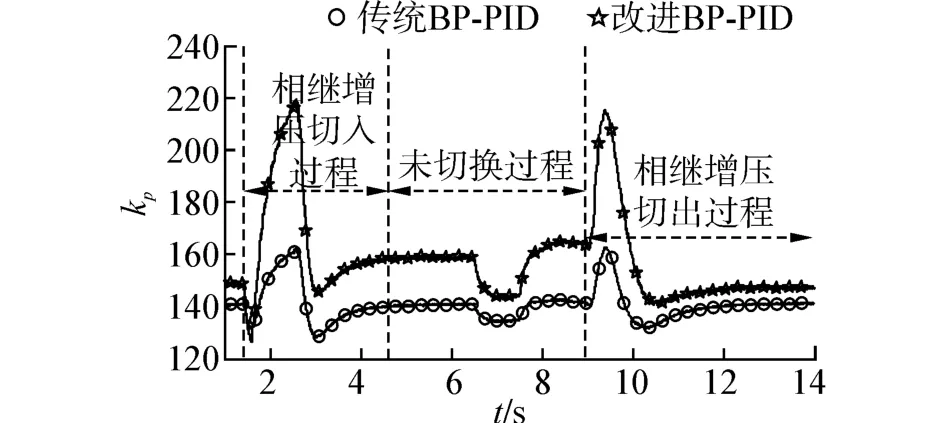
图5 2种调速器的比例参数kp变化曲线对比图Fig.5 Comparison curve of kpwith different speed governors
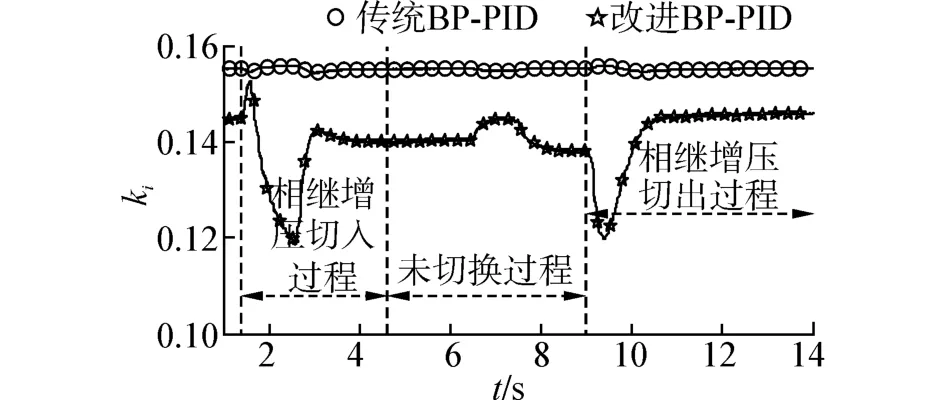
图6 2种调速器的积分参数ki变化曲线对比图Fig.6 Comparison curve of kiwith different speed governors

图7 2种调速器的微分参数kd变化曲线对比图Fig.7 Comparison curve of kdwith different speed governors
由图3、4可以看出,相继增压切入过程中,排气压力最大值为 158 kPa,最小值为120 kPa,相差38 kPa;进气压力最大值为 140 kPa,最小值为106 kPa,相差34 kPa。切出过程中,排气压力最大值为157 kPa,最小值为116 kPa,相差41 kPa;进气压力最大值为141 kPa,最小值为109 kPa,相差32 kPa。未切换过程中,排气压力最大值为127 kPa,最小值为120 kPa,相差7 kPa;进气压力最大值为127 kPa,最小值为122 kPa,相差5 kPa。
图5~7分别为采用传统BP-PID和改进BPPID 2种不同调速器的比例参数kp、积分参数ki、微分参数kd变化曲线对比图。为方便对比,本文引入比幅度rs,其定义式为
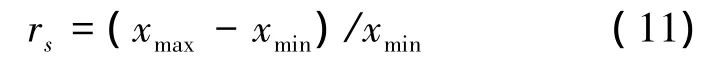
图5~7中传统BP-PID调速器和改进BP-PID调速器kp、ki、kd对比结果如表2所示。由表2可以看出,采用传统BP-PID调速器时,在相继增压切入过程中,kp变化比幅度为0.227,ki变化比幅度为0.01,kd变化比幅度为0.078。在未切换过程中,kp变化比幅度为0.06,ki变化比幅度为0.0026,kd变化比幅度为0.02。在相继增压切出过程中,kp变化比幅度为0.235,ki变化比幅度为0.007,kd变化比幅度为0.07。
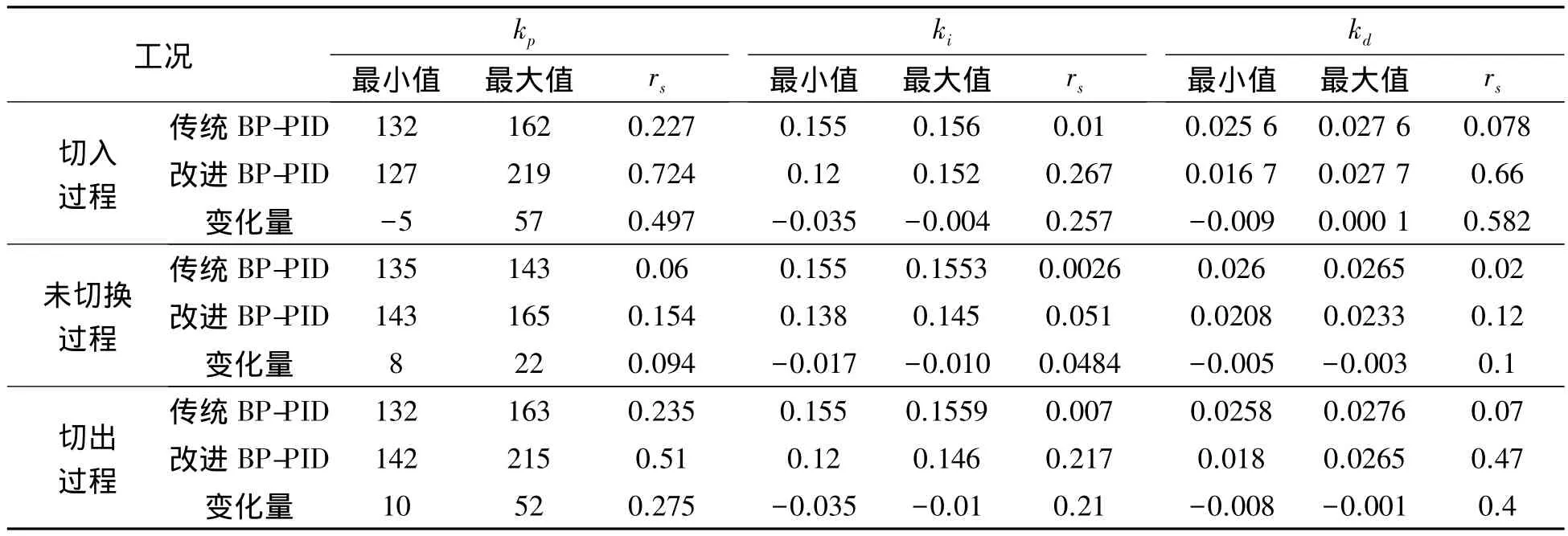
表2 传统BP-PID调速器和改进BP-PID调速器kp、ki、kdTable 2 Comparisons of kp、kiand kdbetween traditional and improved BP-PID governors
相比传统BP-PID调速器,采用改进BP-PID调速器时,在相继增压切入过程中,kp变化比幅度为0.724,增大了0.497;ki变化比幅度为0.267,增大了0.257;kd变化比幅度为0.66,增大了0.582。在未切换过程中,kp变化比幅度为0.154,增大了0.094;ki变化比幅度为0.051,增大了0.048 4;kd变化比幅度为0.12,增大了0.1。在相继增压切出过程中,kp变化比幅度为0.51,增大了0.275;ki变化比幅度为0.217,增大了0.21;kd变化比幅度为0.47,增大了0.4。
由上述对比结果可以看出,在切入过程、未切换过程和切出过程中,相比传统BP-PID调速器,采用改进BP-PID调速器时比例、积分、微分参数的变化比幅度均有所增加;切入和切出过程中比例、积分、微分参数变化比幅度增加量较大,而未切换过程中比幅度增加量很小。说明把进排气压力加入到BPPID的输入空间可以加快BP神经网络对PID参数的调节速度,从而改善调速性能;把进排气压力加入到BP-PID的输入空间,当进排气压力变化较小时,对调速性能的改善较小,而当进排气压力变化较大时,则对调速性能的改善较大。
改进的BP-PID调速器可以明显减小相继增压切换过程中的转速波动,进而可以减小切入设定转速和切出设定转速间的差值,减小舍弃节油区的面积,进一步提高柴油机经济性。
5 结论
对于会产生进排气压力较大波动的柴油机,为进一步提高其调速性能,本文建立了传统BP-PID调速器仿真模型,并在此基础上建立了改进BP-PID调速器仿真模型,以相继增压柴油机为例,分别采用增量式PID、传统BP-PID、改进BP-PID调速器模型进行了相继增压切换过程仿真计算,对结果进行分析,得出结论:
1)相比增量式PID调速器,BP-PID调速器能根据柴油机工况变化自适应调整PID参数,明显减小超调量和稳定时间,调速性能更好;BP-PID调速器可以拓宽输入项的选取范围。
2)把进排气压力加入到BP-PID调速器算法的输入空间可以加快BP神经网络对PID参数的调节速度,从而改善BP-PID调速器的调速性能。
3)在进排气压力波动不大时,相比传统BP-PID调速器,改进BP-PID调速器对调速性能的改善较小;而在进排气压力波动较大时,改进的BP-PID调速器的调速性能明显优于传统BP-PID调速器。对于采用相继增压(STC)、可调二级增压、VGT和EGR技术的柴油机,把进排气压力加入到BP-PID调速器算法的输入空间以提高其调速性能十分有意义。
4)对于具有相继增压和可调二级增压系统的柴油机,改进的BP-PID调速器能明显减小切换过程中的转速波动,因此可使切换设定转速之间的差值减小,从而减小舍弃节油区的面积,进一步提高了柴油机经济性。
[1]ZHANG Qingning,PENNYCOTT A,BRACE C J.A review of parallel and series turbocharging for the diesel engine[J].Journal of Automobile Engineering,2013,227(12):1723-1733.
[2]WAHLSTRÖM J,LARS E,NIELSEN L.EGR-VGT control and tuning for pumping work minimization and emission control[J].IEEE Transactions on Control Systems Technology,2010,18(4):993-1003.
[3]OH B,LEE M,PARK Y,et al.VGT and EGR control of common-rail diesel engines using an artificial neural network[J].Journal of Engineering for Gas Turbines and Power,2013,135(1):012801.
[4]KANG Jun,MENG Wenjun,ABRAHAM A,et al.An adaptive PID neural network for complex nonlinear system control[J].Neurocomputing,2014,135:79-85.
[5]徐戊矫,李武华,王玉松,等.基于BP神经网络和SQP算法的轮毂锻模优化设计[J].重庆大学学报,2014,37 (3):16-22.
XU Wujiao,LI Wuhua,WANG Yusong,et al.BP neural network and SQP algorithm for the optimization of wheel die cavity[J].Journal of Chongqing University,2014,37(3): 16-22.
[6]谢飞,刘永阔,李梦堃.基于灰色-神经网络的核动力设备运行趋势预测[J].应用科技,2014,41(4):10-13,68.
XIE Fei,LIU Yongkuo,LI Mengkun.Research on the operating trend prediction of the nuclear power plants based on gray-neural network[J].Applied Science and Technology,2014,41(4):10-13,68.
[7]彭建鑫,金辉,陈慧岩,等.基于PID神经网络自动换挡过程油门调速[J].北京理工大学学报,2011,31(10): 1179-1183.
PENG Jianjun,JIN Hui,CHEN Huiyan,et al.Research on engine speed regulation based on PID neural network in AMT gear shift[J].Transactions of Beijing Institute of Technology,2011,31(10):1179-1183.
[8]石勇,齐自达,孙军,等.船用柴油机齿条位置执行器与转速BP神经网络控制研究[J].内燃机工程,2013,34 (4):42-47.
SHI Yong,QI Zida,SUN Jun,et al.Research on the control of rack position actuator and marine diesel engine speed based on BP neural network[J].Chinese Internal Combustion Engine Engineering,2013,34(4):42-47.
[9]王银燕,杜剑维,王贺春,等.基于GT-power与Simulink的发动机及其控制系统仿真[J].系统仿真学报,2008,20(16):4379-4381,4386.
WANG Yinyan,DU Jianwei,WANG Hechun,et al.Simulation of engine and control system based on GT-power and Simulink[J].Journal of System Simulation,2008,20(16): 4379-4381,4386.
[10]WAHLSTROM J,ERIKSSON L.Output selection and its implications for MPC of EGR and VGT in Diesel engines[J].IEEE Transactions on Control Systems Technology,2013,21(3):932-940.

