舰船中低频结构噪声源识别方法研究

肖斌，刘文帅，高超，刘志刚

(1.东北电力大学 能源与动力工程学院，吉林吉林132012;2.大连测控技术研究所，辽宁大连116013;3.哈尔滨工程大学动力与能源工程学院，黑龙江哈尔滨150001)

噪声水平及其声隐身性，对发挥舰船作战任务和战术技术性能起着至关重要的作用。为改善舰船噪声水平及声隐身性，其首要任务是解决噪声源识别问题。针对舰船噪声，已发展了多种源识别方法，其中:传统方法在时域上主要有分部运转、时历分析、辐射效率测定和相关分析等，而在频域上主要有谱分析、偏/重相干法、声强测量法、声场空间变换、通过特性法等［1］;也出现一些其他方法，例如:基于MIMO模型的噪声源分析［2］、近场声全息［3］、合成孔径［4］、Doppler频移［5］、功率流法［6］、传递矩阵法［7］等;还形成了一些数值方法，例如:板块元法或有限元分析(FEA)、边界元法(BEM)、统计能量分析(SEA)、FEA-SEA复合方法等［8-11］。

在舰船噪声中，除螺旋桨、流体激励直接辐射声等之外，舰船壳体结构在其声源激励及声振传递中均表现极其重要作用［12］。对于实际舰船壳体结构，激励源具有强相关性，其通道传递具有强耦合性;声源定位结果受到测量孔径效应和声源指向性影响较大，其声振传递通道信息缺失;以及系统参数尚未完全可知，其模型参数、边界条件存在不确定性等。上述使得现有舰船壳体结构噪声源识别方法呈现出一定局限性［1，12］，于是，本文针对舰船壳体结构的多源相关通道耦合中低频振动，考虑系统不确定性，进行噪声源识别策略研究。

1 舰船中低频结构噪声模型

实际舰船壳体结构具有线形复杂、结构耦合且同时受机械设备振动、螺旋桨－轴和流体共同激励等特征［12］。其中:

1)壳体，在局部模态与激励频率耦合时，或与机械振源连接成为振动传递通道节点时，抑或毗邻上层建筑及附体并因其局部湍流脉动压力增强而受到激励［13］时，引起结构振动声辐射。

2)艉部，单纯作为壳体局部产生结构振动声辐射，或者在桨轴系统激励下，横向振动分别通过推力轴承和中间轴承再经耐压壳体、支撑等传入外壳，而纵向振动通过尾部轴承传入外壳［6］，形成结构振动声辐射。

3)相关激励，当机械设备因同时运行而在其特征线谱或窄带频谱上出现频谱叠合现象［2］时，以及桨轴激励船体振动在其特征线谱或窄带、宽带频谱上与船体结构(整体或局部)模态耦合并出现与机械噪声频谱叠合现象时，通过振动能量多途传递形成耦合振动。

4)中低频段，在舰船声学总体设计机械噪声控制设计中水下辐射噪声限制线由机械振源振动特性和实船安装结构特性共同决定［14］，此时壳板结构产生主要的水下结构声辐射［15］。

5)系统不确定性，当考虑板壳结构受到材料不均匀性、制造工艺及其板上附件的加工、安装等影响［16］而使系统参数存在随机性时，或考虑舰船实际航行状态、海况条件及其辅机系统、随动设备运行等差异［2，15］而使系统边界具有随机性时，通过舰船壳体结构系统建模形成其系统模型、参数或边界条件具有随机性的动力系统。

综上，对于舰船壳体结构，考虑系统不确定性，加之机(械)－机(械)及桨轴激励船体的耦合振动，形成多源相关多通道耦合中低频随机振动系统模型。

2 中低频结构噪声源识别策略

对于舰船中低频结构噪声模型，考虑系统不确定性具有显著统计特征，在通道传递、响应等成为随机量情况下，通过系统响应、通道传递、激励源的统计特征分析过程，实现其激励源识别。

2.1 响应及其统计分析

2.1.1 系统动力响应

对于动力系统，按照单一结构(梁、板壳结构或空间声场等)纵振、横振及弯振等模态振型进行子结构划分，通过模态分析估计系统前n(n=1，2，…)阶固有频率ωn、模态振型φn=［φn(x1)，φn(x2)，…，φn(xN)］T和模态阻尼ηn等，在单频分布载荷{p(x)ejωt}作用下位置x处的系统响应

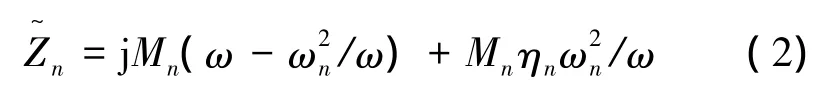
若式(1)考虑集中力作用，则在x处微元面定义广义力F

～=p(x0)dx0，可得系统均方速度响应［17］

在式(3)中，受到统计独立同分布(independent identically distributed，IID)激励时，对均方速度在空间上进行平均，即

式中:＜·＞为集合平均。

当受到宽频激励时，若激励频带［ω1，ω2］内模态数N≥5，系统呈现高频振动［10］。在式(3)中，激励均方幅值代替，得到带宽Δω(= ω2－ω1)上系统均方速度响应:

在高频振动中，参数间统计特性显著、模态参数分布趋于统计稳定［10］，全局模态密度主导着系统振动特征，此时在稳态条件下SEA建立能量平衡方程，即

式中:子系统i的模态密度ni，耦合损耗因子ηij，内损耗因子ηii和输入功率Pinj，i，子系统能量Ei。

对于简单动力系统，式(6)代替式(5)，避开ωn、φn及计算和复杂积分运算，直接通过Pinj，i、ηii、ni和ηij等描述耦合子系统振动。而对于复杂耦合系统，结合 FEA、模态综合(component mode synthesis)和周期结构理论(periodic structure theory)，基于传播波频散曲线建立子系统SEA模型参数［18］。亦即:对于第i复杂耦合子系统，若其固有频率Ωn，有

式中:动刚度矩阵D=K+jωC－ω2M，相移变换矩阵R=R(kn，θn)，φn满足φHn(RHMR)φn=1。

通过在波数空间对频散曲线kn进行积分，给出复杂耦合子系统模态密度:

及其系统平均内损耗因子［19］

式中:ηr、Kr为子系统第r个区域的阻尼损耗因子、子系统总刚度贡献量。对应的子系统振动能量为

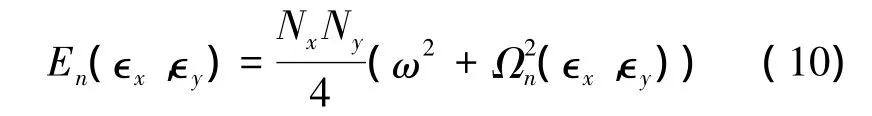
当ω=Ωn，出现共振时，式(10)中振动能量变为NxNyω2/2，式(9)中ηnn亦可得到简化［18］。

在式(10)中，模态能量叠加得到子系统平均振动能量，继而得到子系统速度响应互谱矩阵:

在中低频随机振动中，局部模态参数主导系统振动特征。此时基于FEA建模，在ωn、φn、Z～n与Pinj，i、ηii、ni、ηij之间建立随机特征传递，引入描述直达场与混响场响应特性的扩散场互易关系［11］:

式中:I(·)为复数虚部，Ddir=E［D］，frev为混响场等效力。

于是，在式(6)基础上，得到FEA-SEA复合建模公式:

对比式(6)或(13)通过FEA建模引入确定模型激励输入功率及阻尼内耗散因子，即

考虑IID广义力激励，基于原点、跨点阻抗［17］式(5)以及基于能量平衡［10，20］式(6)或式(13)，在模态能量均分假设下，其系统响应预测结果具有很好的一致性。然而，进一步考虑系统模态能量非均分情况，引入统计模态能量分布分析(statistical modal energy distribution analysis，SmEdA)［21］，通过FEA获取子系统模态信息并与之建立自然联系，以实现模态能量非均分子结构振动能量空间分布估计，即

式中:下角标i、j、k为子系统序号，p、q为子系统模态序号，上角标R、NR代表子系统间共振、非共振模态参数;(N)R项为通过(非)共振模态在子系统间模态能量传递。从而，获得第i子系统在位置x处平均动能和势能［21］:

式中:Mp为第p阶模态质量，Mx、Kx、φp(x)为位置x处质量、刚度矩阵和解耦子系统模态振型。

在式(18)中，若系统满足模态能量均分且固有频率在Δω内满足IID分布，则对式(19)和(20)进一步得到简化，得到第i子系统在位置x处均方速度:

2.1.2 响应统计特性

基于式(13)和(18)在时间、空间上平均的系统响应估计，若存在确定激励空间位置分布及响应集中，相比系统实际响应则存在很大差异，因而计算系统均值响应在不同位置上的方差，分析系统均值响应的空间相关效应，以获得类似式(19)和(20)的具体空间位置分布的系统响应估计。

对于简单耦合系统，在第i子系统随机选择位置xinj，i激励、第j子系统随机选择位置xob，j响应、耦合位置为xcpl，(·)。由于系统模态参数服从Poisson分布［10］，则针对式(21)，其均方速度响应相对方差［22］为

其中，RelVar［·］=Var［·］/E［·］2，Var［·］为方差。而在Δω内当第i子系统受到IID白噪声激励时，式(22)简化为［10，22］

对于复杂耦合系统，在模态参数一致性假设下，模态参数服从GOE分布［11，20］，此时针对式(17)确定子系统响应方差为［11］

2.2 通道传递统计分析

2.2.1 固有频率统计特性

考虑系统不确定性时，其固有频率计算涉及到随机本征值问题。对于无阻尼或比例阻尼随机动力系统，其系统离散方程:

其中，质量随机矩阵M(X):RmaRN×N、刚度随机矩阵K(X):RmaRN×N对X∈Rm连续且二阶以上可微，系统矩阵S:=M－1K∈RN×N，系统(矩阵S)第j阶本征值λj=ω2j对应模态振型φj;将固有频率按照ω1＜ω2＜… ＜ωN升序排列，通过联合概率密度函数(joint probability density function，JPDF) pX(X):RmaR建立固有频率JPDF p(ω)。

在高频随机振动中，较之在简单耦合系统中的Poisson分布，在复杂耦合系统中模态参数服从Guass系综(GOE/GUE)分布［11，20］，考虑定义关系［23］:

式中:Rn称为n点相关函数，Tn称为n级聚类函数，G∈∪mGm。将频率划分n个邻域ωj＜ω ＜ωj+ dωj，直接利用RMT确定Tn，并建立导出函数Rn，从而计算系统前n阶固有频率JPDF。

在中低频随机振动中，式(26)中系统矩阵不满足Gauss系综分布，导致在式(28)中Tn函数性质依赖于系统随机程度和频率变量，因而利用Tn函数性质借助随机系统参数建模确定Tn、计算Rn，最终获得系统前n阶固有频率JPDF。此时，复杂系统参数建模在模型数据的获取和参数统计特征向p(ω)概率迁移等面临巨大挑战。然而，基于摄动理论已获得较好的本征值分析结果［24］。亦即，采用随机摄动理论，针对本征值λj，有

以及Hessian矩阵Dλj，μ为

假设Λj～pΛj(λj)，通过中心化 Λj，得到随机变量 Zj～pZj(ζj)。结合式(26)，估计λj前r阶矩，考虑PDF定义式性质及统计矩约束条件，基于Shannon熵并利用Jaynes最大熵原理，有［24］

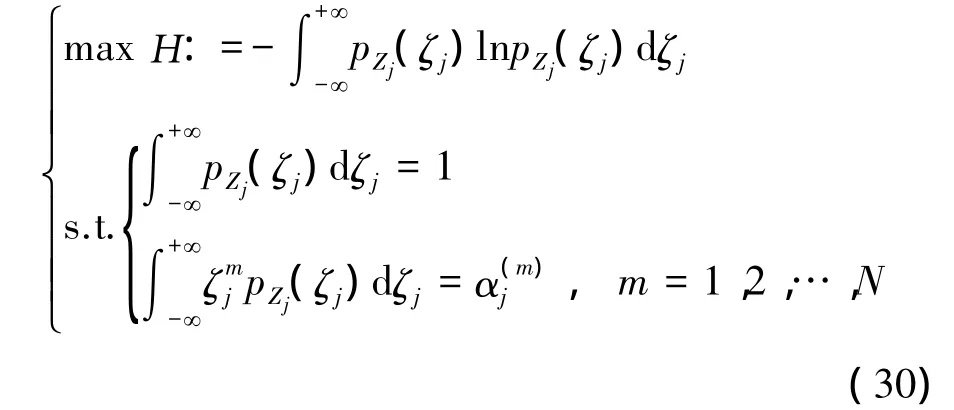
通过Euler-Lagrange方程求解，得

其中

在式(29)中，当考虑λj高阶矩时，形成非线性方程，需采用数值解法估计ρm(m=0，1，…，N)，进而通过式(31)给出pΛj(λj)，j=1，2，…，N。

2.2.2 模态振型统计特性

对于动力系统，本征值与本征函数具有伴随关系，使得固有频率与模态振型的统计特性具有一致性。针对式(26)定义的系统矩阵S，基于摄动理论，若引入随机矩阵P∈RN×N，正值小量ε，将其表达为=S+εP，则得到摄动模态振型表达式［25］:

在此基础上，基于式(29)计算出系统本征值PDF，利用摄动本征值、模态振型的伴随关系:

来分析模态振型统计特性。

2.2.3 通道传递统计特性

在激励与响应之间传递路径借助频响函数建立两者振动传递关系，而激励源识别还需建立传递路径逆向关系，传递路径正/逆向关系构成系统振动传递通道。

考虑波动法式(34)，在位移场理论假设下实现系统控制方程精确求解，可获得系统任意阶次的固有频率及模态振型［26］，并建立激励源与速度响应的随机频响函数矩阵:

通过X a［M(X)，C(X)，K(X)］一、二阶敏感度分析获得正定实参数矩阵［MR(X)，CR(X)，KR(X)］，实现随机频响函数降阶建模［27］;利用MSC方法、或XaH(jω，X)的一、二阶摄动方法，估计H(jω，X)及其矩阵均值E［H(jω，X)］，进而可得

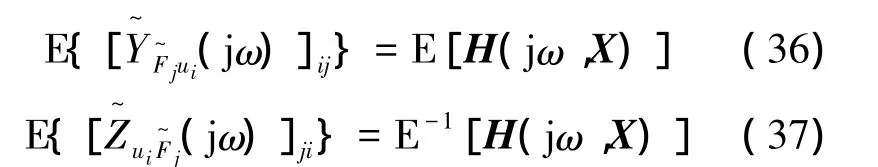
为分析系统激励或响应的空间分布特性，基于模态法引入与波动法式(34)等效的动刚度D(jω)与柔度ρ(jω)。于是，结合式(1)和(34)，利用模态叠加原理，并代入式(2)，可得

式中:φ⊥(xi)=［φ1(xi)，…，φn(xi)，…］;i=j时动刚度对应于原点阻抗，i≠j时动刚度对应于跨点阻抗。

对于随机动力系统，传递通道及其通道耦合作用表现为动刚度/柔度矩阵统计特性。在式(26)中固有频率、模态振型为随机变(向)量，考虑模态振型正交性，可知ρ∈(R)为正定实对称矩阵，且当j≤k，矩阵元素ρjk统计独立等性质。从而有

考虑固有频率、模态振型的统计特性，基于Shannon熵并利用Jaynes最大熵原理［27］，得

2.3 激励源统计分析

2.3.1 子系统激励源特征

针对随机动力系统，基于能量方法式(6)、(13)或(18)建立系统能量平衡方程，子系统激励源不具有空间分布特征，通过子系统振动能量分布初步估计子系统激励源分布，于是定义路径振动能量传递系数为［28］

式中:ηii为传递路径上子系统内耗散因子(由或ηii，p组成)为传递路径上的耦合耗散因子(由或组成)。

根据式(44)，利用式(6)、(13)或(18)中模型参数，计算路径振动能量传递系数τs12…t，进行振动传递通道贡献排序，基于SEA模型节点－路径树状图提出K域能量传递路径算法［28］确定主要传递通道，最终确定子系统激励源分布特征。

2.3.2 激励源统计特性

在子系统激励源特征识别基础上，考虑单纯系统随机性时固有频率、模态振型的统计特性以及空间相关性时激励源的位置不确定性，使得集中作用激励源仍具有复杂的统计特性。

并结合式(19)和(20)中子系统激励源特征识别结果，估计其空间位置分布统计特性。

同时，按照式(45)中激励源、响应的空间位置均值张成传递通道矩阵空间，建立系统随机动刚度/柔度矩阵，通过

并结合式(42)随机动刚度/柔度矩阵的PDF，估计激励源谱统计特性。

3 结束语

针对舰船壳体结构的机(械)－机(械)及桨轴激励船体中低频耦合随机振动，建立舰船中低频结构噪声模型。考虑现有噪声源识别方法针对相关多源激励通道耦合、系统不确定性等模型存在着局限性，本文基于随机动力系统响应、通道传递和激励源等统计特征分析提出中低频结构噪声源识别策略，即:通过讨论随机动力系统响应及其统计特性、基于模态法的随机动刚度/柔度矩阵、波动法的机械阻抗/导纳、能量法的振动能量传递系数等分析通道传递，通过激励源统计分析识别子系统激励源，获得激励源位置分布、谱特征等统计特性，最终以统计的观点实现中低频结构噪声系统激励源识别。

本文提出的中低频结构噪声源识别策略，为舰船中低频结构噪声源识别技术的发展提供一种思路，为舰船中低频结构噪声源识别发展指出探索方向。然而，提出的噪声源识别策略，在中低频舰船结构噪声的随机系统建模、本征分析、中低频激励源空间位置分布统计分析以及激励源统计特征及其置信区间分析等，还有待于进一步研究和探索。

［1］杨德森.水下航行器噪声分析及主要噪声源识别［D］.哈尔滨:哈尔滨工程大学，1998:70-98.

YANG Desen.Noise sources identification and analysis for under-water vehicles［D］.Harbin:Harbin Engineering University，1998:70-98.

［2］王之程，陈宗岐，于沨，等.舰船噪声测量与分析［M］.北京:国防工业出版社，2004:36-242.

［3］程广福，肖斌，王志伟，等.柱面多参考统计最优近场声全息研究［J］.哈尔滨工程大学学报，2011，32(1):90-97.

CHENG Guangfu，XIAO Bin，WANG Zhiwei，et al.Investigation on cylindrical multi-reference statistically optimized near-field acoustical holography［J］.Journal of Harbin Engineering University，2011，32(1):90-97.

［4］夏春艳，刘文帅.应用合成孔径技术进行实船噪声源分析［J］.舰船科学技术，2005，27(4):72-73，96.

XIA Chunyan，LIU Wenshuai.Analyzing the noise of warship with the technology of synthetic aperture［J］.Ship Science and Technology，2005，27(4):72-73，96.

［5］杨益新，徐灵基，杨龙.一种基于多普勒频移变化率的舰船线谱噪声源定位方法:中国，201310068551［P］.2013-07-10.

［6］冯国平，黄修长，刘兴天，等.基于振动功率流的船艉传递路径分析［J］.噪声与振动控制，2010，30(2):5-8.

FENG Guoping，HUANG Xiuchang，LIU Xingtian，et al.A-nalysis of transmission paths of ship stern vibration based on power flow theory［J］.Noise and Vibration Control，2010， 30(2):5-8.

［7］肖斌，李彪，夏春艳，等.基于功率流法双层隔振系统振动传递［J］.机械工程学报，2011，47(5):106-113.

XIAO Bin，LI Biao，XIA Chunyan，et al.Power flow method used to vibration transmission for two-stage vibration isolation system［J］.Journal of Mechanical Engineering，2011，47(5):106-113.

［8］郑国垠，范军，汤渭霖.考虑遮挡和二次散射的修正板块元算法［J］.声学学报，2011，36(4):377-383.

ZHENG Guoyin，FAN Jun，TANG Weilin.A modified planar elements method considering occlusion and secondary scattering［J］.Acta Acustica，2011，36(4):377-383.

［9］曹贻鹏.推进轴系引起的艇体结构振动与辐射噪声控制研究［D］.哈尔滨:哈尔滨工程大学，2008:15-44.

CAO Yipeng.Study on underwater structure vibration and radiated noise control caused by propeller exciting force［D］.Harbin:Harbin Engineering University，2008:15-44.

［10］LYON R H.Statistical energy analysis of dynamical systems:theory and applications［M］.Cambridge:MIT Press，1975:65-169.

［11］LANGLEY R S，COTONI V.Response variance prediction for uncertain vibro-acoustic systems using a hybrid deterministic-statistical method［J］.The Journal of the Acoustical Society of America，2007，122(6):3445-3463.

［12］肖斌.舰船壳体结构噪声分离技术研究——非线性频谱特征及特征谱分离策略［J］.声学学报，2013，38(3): 346-353.

XIAO Bin.Investigation of ship hull structural noise separation technique——nonlinear frequency spectrum features and its characteristic spectral separation strategy［J］.Acta Acustica，2013，38(3):346-353.

［13］胡其望.潜艇指挥台围壳模型噪声机理研究［D］.哈尔滨:哈尔滨工程大学，2007:74-102.

HU Qiwang.Research of noise mechanisms of submarine sail model［D］.Harbin:Harbin Engineering University，2007:74-102.

［14］魏强，朱祥.中低频振动计算中有限元建模方法的讨论［J］.中国舰船研究，2006，1(1):66-69.

WEI Qiang，ZHU Xiang.Discussion on FEM modelling in the numerical calculation of mechanic vibration［J］.Chinese Journal of Ship Research，2006，1(1):66-69.

［15］孙雪荣，朱锡.船舶水下结构噪声的研究概况与趋势［J］.振动与冲击，2005，24(1):106-113.

SUN Xuerong，ZHU Xi.Survey and tendency of study on the underwater noise of ship structure［J］.Journal of Vibration and Shock，2005，24(1):106-113.

［16］李舜酩，廖庆斌，尚伟燕.随机质量板的振动响应及其统计分析［J］.振动工程学报，2009，22(1):60-64.

LI Shunming，LIAO Qingbin，SHANG Weiyan.Analyses of vibration responses and its statistical characteristics for random mass plate［J］.Journal of Vibration Engineering，2009，22(1):60-64.

［17］FAHY F，GARDONIO P.Sound and structural vibration: radiation，transmission and response［M］.2nd ed.New York:Academic press，2007:75-242.

［18］COTONI V，LANGLEY R S，SHORTER P J.A statistical energy analysis subsystem formulation using finite element and periodic structure theory［J］.Journal of Sound and Vibration，2008，318(4/5):1077-1108.

［19］LANGLEY R S.On the modal density and energy flow characteristics of periodic structures［J］.Journal of sound and vibration，1994，172(4):491-511.

［20］SHORTER P J，LANGLEY R S.Vibro-acoustic analysis of complex systems［J］.Journal of Sound and Vibration，2005，288(3):669-699.

［21］MAXIT L，EGE K，TOTARO N，et al.Non resonant transmission modelling with statistical modal energy distribution analysis［J］.Journal of Sound and Vibration，2014，333 (2):499-519.

［22］JI L，MACE B R.Statistical energy analysis modelling of complex structures as coupled sets of oscillators:ensemble mean and variance of energy［J］.Journal of Sound and Vibration，2008，317(3-5):760-780.

［23］MEHTA M L.Random Matrices［M］.3rd ed.Singapore: Elsevier Pte Ltd.，2004:33-181.

［24］ADHIKARI S，FRISWELL M I.Random matrix eigenvalue problems in structural dynamics［J］.International Journal for Numerical Methods in Engineering，2007，69(3): 562-591.

［25］ALLEZ R，BOUCHAUD J P.Eigenvector dynamics:general theory and some applications［J］.Physical Review E，2012，86(4):046202.

［26］PAGANI A，BOSCOLO M，BANERJEE J R，et al.Exact dynamic stiffness elements based on one-dimensional higher-order theories for free vibration analysis of solid and thinwalled structures［J］.Journal of Sound and Vibration，2013，332(23):6104-6127

［27］SOIZE C.A nonparametric model of random uncertainties for reduced matrix models in structural dynamics［J］.Probabilistic Engineering Mechanics，2000，15(3):277-294.

［28］XIE S L，ZHANG Y H，XIE Q，et al.Identification of high frequency loads using statistical energy analysis method［J］.Mechanical Systems and Signal Processing，2013，35(1/2):291-306.