局部平均刚度比对底框结构抗震性能的影响

邓宏宇，孙柏涛，2

(1.哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001;2.中国地震局工程力学研究所地震工程与工程振动重点实验室，黑龙江哈尔滨150080)

底框结构是指底层或底部两层为框架－抗震墙，上部为砌体结构的混合承重房屋，在我国中小城镇的临街建筑中应用十分广泛。该结构类型是由2种不同承重和抗侧力体系所构成的混合结构，结构竖直方向上刚度变化剧烈、上刚下柔，属于不利于抗震的一种结构体系。在以往的研究过程中，我国学者对底框结构刚度控制的研究主要集中在结构竖向刚度的合理分布上［1-3］。随着我国经济的发展，房屋使用面积不断增加，平面布置日趋复杂。有时会因为使用功能的需要形成局部的大空间，造成结构平面内刚度分布不均匀、局部刚度不足，使楼层产生偏心距，在地震作用下发生扭转。局部刚度较低的区域成为楼层内的薄弱环节，在地震作用下率先破坏，即使结构整体看上去破坏并不严重，也会由于局部墙体的严重破坏而导致结构整体使用功能丧失。目前有关结构平面内刚度的不均匀性对底框结构抗震性能造成的影响研究很少，我国抗震规范中也没有相关的控制指标，因此开展这方面的研究工作具有十分重要的意义。

本文提出了局部平均刚度比的概念，并以汶川地震中一栋严重破坏的底框结构住宅楼为例，设计了7个对比有限元模型并进行弹塑性时程分析，研究了局部平均刚度比与墙片破坏的对应关系，给出了底框结构局部平均刚度比的建议取值范围，为抗震设计提供参考。

1 局部平均刚度比的定义

1.1 底框结构震害实例

天河馨苑4号楼位于四川省绵竹市，结构形式为底框结构，总层数为6层，底层为商店，2～6层为住宅(图1(a))。该结构建于2001年，按Ⅱ类场地，7度0.1g抗震设防设计。汶川地震中该栋建筑处于Ⅸ度区，破坏情况为:结构首层部分填充墙墙体出现剪切斜裂缝，框架柱、框架梁和混凝土抗震墙破坏轻微;上部砌体层破坏较为严重，尤其是第2层过渡层砌体中右侧山墙转角部位的多道承重、非承重墙体有贯穿斜裂缝(图1(b)、(c))，楼梯间墙体开裂，表面砂浆掉落(图1(d))。该建筑的震害等级最终评定为严重破坏。

图1 实例结构破坏情况Fig.1 Damage of the instance structure

1.2 震害原因分析

通过考察实例结构上部砌体层平面图(图2)，发现A、B 2个区域面积大致相等，A区出于增大使用空间的考虑，形成了较为空旷的大开间，该区域内墙体较少，局部刚度较低，实际震害中A区内的4道墙体破坏也是最严重的。相比之下，区域B处房间开间适中，刚度分布比较均匀，墙体的破坏较轻。同时由于平面内刚度不均匀分布，楼层存在偏心距，A区成为远离刚心的区域，在地震作用下结构发生的扭转效应也加重了A区墙体的破坏。

图2 实例结构上部砌体层平面图Fig.2 Floor plan of upper masonry of the instance structure

该结构经过正规抗震设计和施工，侧向刚度比等指标满足规范要求，楼层平面内其他墙体只达到中等破坏。但由于A区4道墙体严重破坏，丧失承载力，使得整体结构无法继续正常使用，震害等级上升为严重破坏。由此可见，当楼层整体总刚度满足规范要求时，平面内刚度分布的均匀性、局部刚度的大小也会对底框结构抗震性能产生很大影响。

1.3 局部平均刚度比的概念

为表征平面内刚度分布的均匀性，提出了局部平均刚度比的概念作为衡量局部区域内刚度大小的指标。

1.3.1 定义及计算方法规定

将作为研究对象的楼层视为一个整体，按照墙体抗侧刚度计算公式统计楼层内所有墙体的总刚度，再将其平均分配到楼层总平面面积上，定义为层间平均刚度，其反映的是楼层整体单位面积上刚度大小的平均水平。计算公式为

式中:W为层间平均刚度，kN/m3;K为层间总刚度，kN/m;S为楼层总平面面积，m2。

将所要研究的局部区域单位面积上的刚度平均值定义为局部平均刚度:

式中:W0为局部平均刚度，kN/m3;K0为局部总刚度，kN/m;S0为局部平面面积，m2。对于局部平均刚度的计算方法，做出以下几点规定:1)局部平均刚度的计算范围是以计算区域四周墙体所在的轴线为边界;2)对于处于边界内部的墙体，刚度全部计入该区域的局部刚度;3)对于处于边界轴线上的墙体，刚度取一半计入该研究区域的局部总刚度;若处于边界轴线上的墙体为山墙或外纵墙，则刚度全部计入该区域的局部刚度。

将楼层层间平均刚度的大小归一化为1，局部平均刚度与楼层层间平均刚度的比值记为局部平均刚度比α:

局部平均刚度比α是一个无量纲的数，其物理意义是:同一楼层内，局部区域刚度的大小与整层刚度平均水平的比值。

1.3.2 实例结构局部平均刚度比的计算

以图2中的A区为例，应用式(1)～(3)，说明局部平均刚度比的计算方法。A区域内4道墙片分别记为Q1～Q4，如图3(a)所示。墙片刚度的计算采用文献［4］中的公式，其中X向刚度由墙片Q1和Q3提供，Y向刚度由墙片Q2和Q4提供。墙片Q1、Q3和Q4处于轴线上，对应刚度K1、K3和K4的一半计入到区域A的局部刚度中;墙片Q2为处于轴线上的山墙，对应刚度K2全部计入区域A的局部刚度。KA0、SA0和WA0表示区域A的局部刚度、局部平面面积和局部平均刚度。实例结构A区局部平均刚度比αA计算结果见表1。

表1 实例结构A区局部平均刚度比Table 1 Local average stiffness ratio of region A of the instance structure

由表1可以看出，实例结构中A区在X、Y 2个方向的局部平均刚度都远低于层间平均刚度，局部平均刚度比分别只有0.47和0.38，说明该区域刚度只有整个楼层平均水平的47%和38%，是整个楼层中的薄弱部位，与1.2节的震害原因分析相一致。

2 有限元模型的设计和建立

在实例结构上部2～5层中，暂不考虑使用功能的要求，在A区的X、Y 2个方向上逐渐增加墙片数量，逐步提高A区2个方向的局部平均刚度比。B区及平面内其余墙体的布置位置保持不变。设计了包括实例结构在内的共8个模型，通过ABAQUS有限元软件进行弹塑性时程分析，研究底框结构局部平均刚度比与墙片破坏之间的关系。

2.1 模型设计

图3给出设计模型A区处的平面变化情况(括号内数字为设计模型区域A处X、Y 2个方向的局部刚度比)。应用式(1)～(3)分别计算8个模型中区域A和区域B两处的局部平均刚度比，区域B局部平面面积SB0为60.75 m2，KB0、WB0和αB表示区域B的局部刚度、局部平均刚度和局部平均刚度比，详细计算结果见表2。

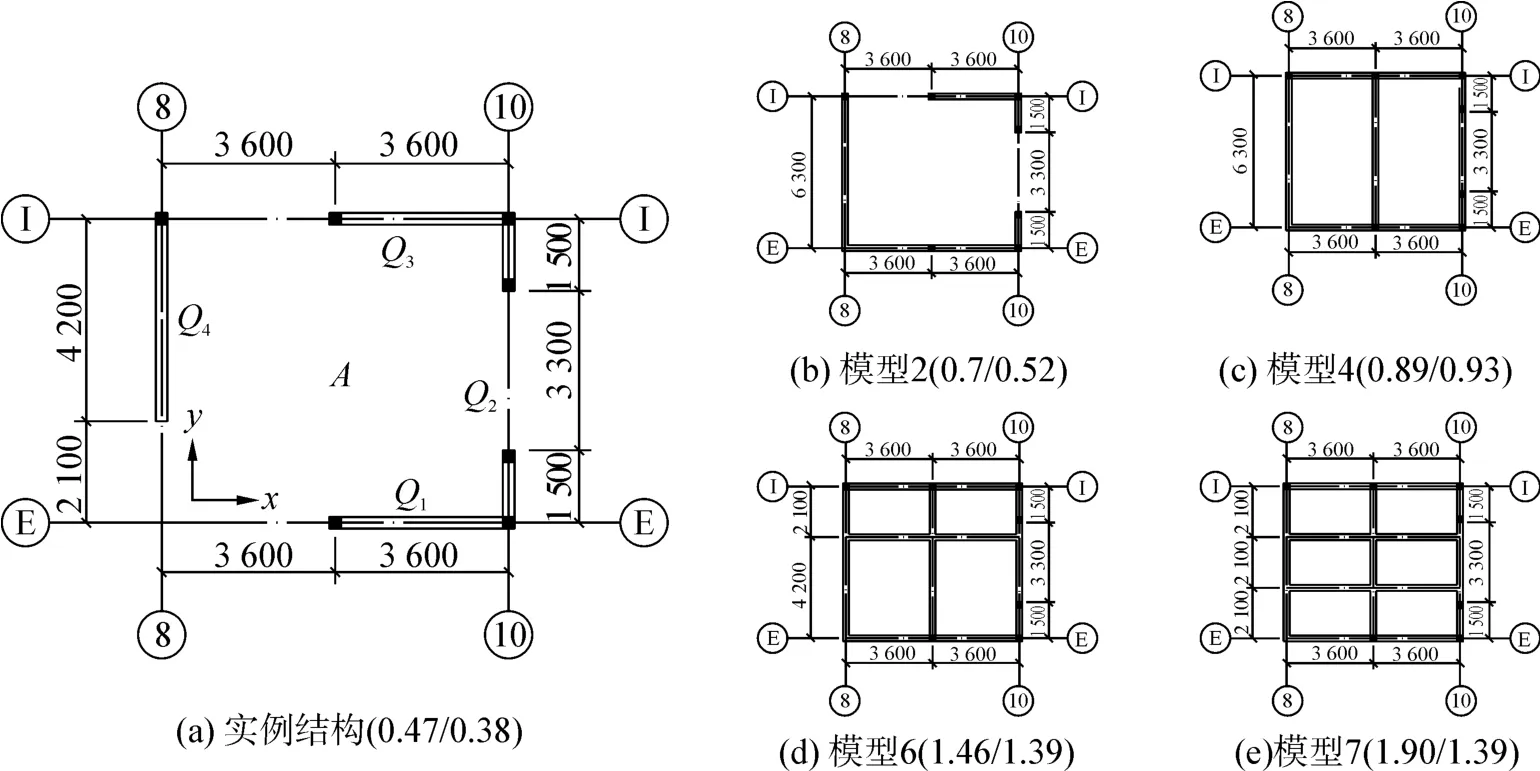
图3 设计模型A区域处平面图Fig.3 Plane graph of region A of design models

从表2可以看出:A区随着墙片数量的增加，局部平均刚度比显著提高，X向上由0.47增大到1.90，Y向上由0.38增大到1.39。B区墙体局部刚度虽然始终保持不变，但由于A区墙体的增加造成整层的层间总刚度增加，因此B区的局部平均刚度比略有降低，X向上由1.39降低为0.94，Y向上由0.8降低为0.66。

2.2 有限元模型的建立

通过ABAQUS建立有限元模型。底层的框架柱、框架梁和钢筋混凝土抗震墙采用 solid单元(C3D20R)，底层的填充墙按文献［5］中的计算公式简化成对角斜撑杆，斜撑杆采用truss单元(T3D2)，各层楼板和上部普通砖砌体墙采用 shell单元(S4R)。楼板和墙体之间采用constraint中的tie连接，模拟填充墙的桁架杆truss单元(T3D2)与框架柱之间采用connector中的join连接［6］。

2.3 材料的本构关系

2.3.1 混凝土本构关系

混凝土的本构关系采用文献［7］附录中给出的钢筋混凝土构件单轴受压、受拉应力应变关系。混凝土单轴受压应力应变关系采用:

式中:αa和αd为与单轴受压应力应变曲线上升段和下降段有关的参数，f为混凝土单轴抗压强度，εc为与f对应的混凝土峰值压应变。混凝土单轴受拉应力应变关系采用如下公式:

式中:αt为与单轴受拉应力应变曲线下降段有关的参数，f为混凝土单轴抗拉强度，εt为与f对应的混凝土峰值拉应变。

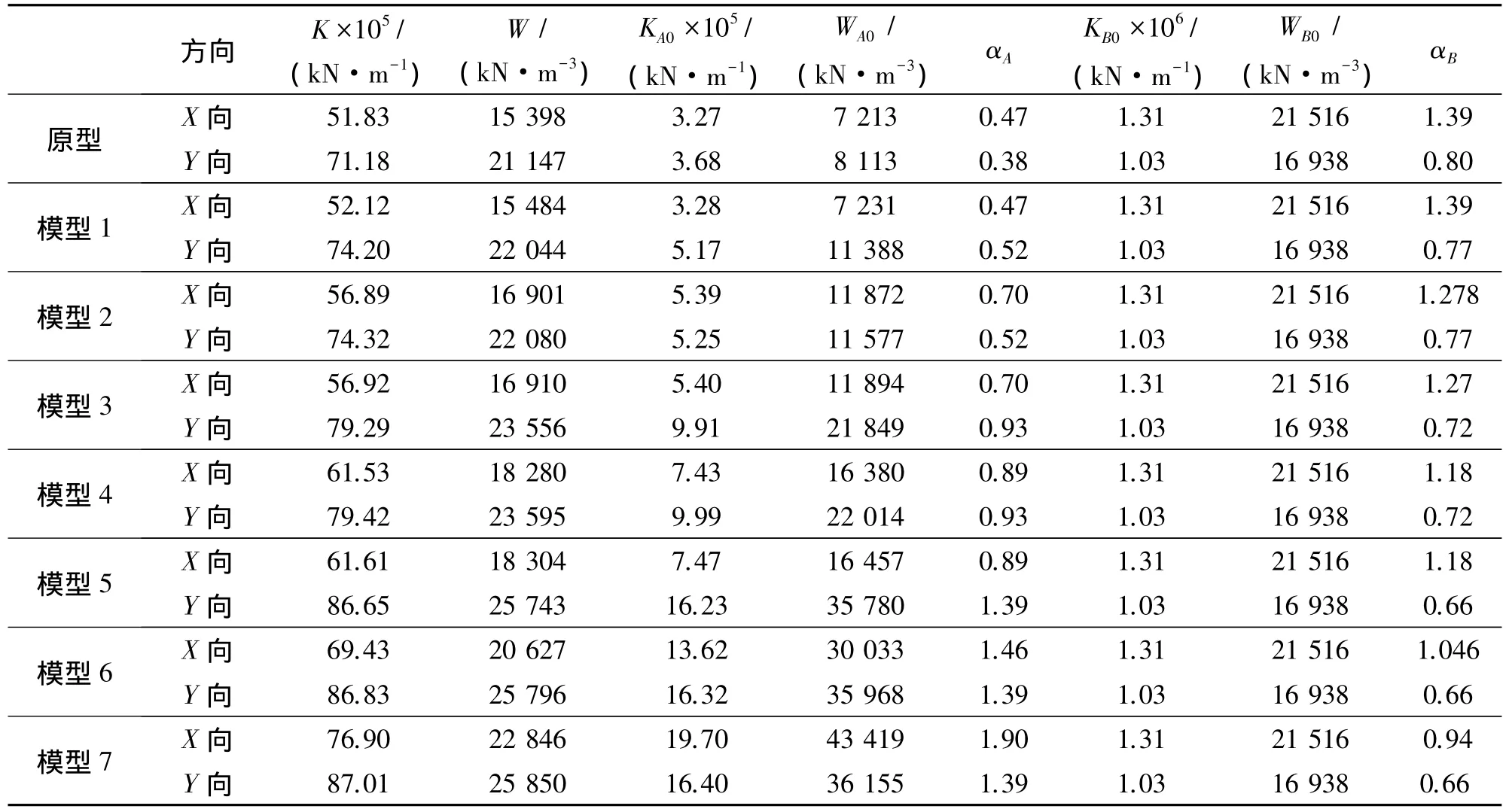
表2 设计模型A、B两处的局部平均刚度比Table 2 Local average stiffness ratio in region A and B of design models

2.3.2 砌体本构关系

采用的砌体本构关系是由施楚贤等［8］基于前人的实验结果，结合我国砌体材料的特点提出的上升段为抛物线、下降段为线性的砌体受压应力应变关系:

式中:fm为砌体平均抗压强度，ε0为砌体材料的峰值压应变。

2.4 地震波的选取

由于结构处于Ⅱ类场地，因此选取汶川地震中在Ⅱ类场地记录到的卧龙地震波作为外部地震动输入。以卧龙波的东西向为例(EW向)，加速度时程和频谱特性见图4。汶川地震［9］中记录到的该结构所在地区地面加速度峰值为0.6g。为模拟结构在地震中的真实反应，将输入的X向卧龙波峰值加速度调整为0.6g，Y向对应成比例缩放。

图4 卧龙波EW向加速度时程及频谱特性Fig.4 Acceleration time history and spectrum curve of Wolong ground motion in EW orientation

3 地震反应计算结果分析

3.1 结构整体地震反应分析

将峰值加速度为0.6g的卧龙波分别输入到以上8个模型中进行弹塑性时程分析。实例结构模型的模拟结果与震害实际相吻合，验证了该建模方法、本构关系和地震波选取的合理性，其他7个设计模型由于A区局部刚度的增加，结构上部砌体层的地震反应有一定程度的降低。

3.2 楼层局部墙体地震反应分析

由于上部砌体层中，第2层破坏最严重、受地震剪力最大，因此提取各个模型第2层A、B 2个区域中的10道墙片作为研究对象，计算墙片的层间位移角和墙片的超越强度倍率［10］。A区中所选墙片和编号见图3(a)，B区中所选墙片和编号见图5。

图5 区域B平面图Fig.5 Plane graph of region B

由于刚度是分方向的，因此计算结果分析也要区分X、Y 2个方向。区域A中处于X向的墙片为Q1和Q3，处于Y向的墙片为Q2和Q4;区域B中处于X向的墙片为Q5、Q6和Q7，区域B中处于Y向的墙片为Q8、Q9和Q10。以上8个模型中，X向上局部平均刚度比有变化的模型为原型、模型2、模型4、模型6和模型7;Y向上局部平均刚度比有变化的模型为原型、模型1、模型3和模型5。

3.2.1 区域A墙片计算结果

分析增加局部平均刚度比对A区墙体破坏状态的改善情况，找出局部平均刚度比的下限值。

1)X向计算结果。

图6(a)中，随着局部平均刚度比的增加，各墙片的层间位移角逐渐降低，在局部刚度比达到0.89之前曲线下降的速率较快，意味着在此之前提高局部刚度会明显改善墙片的侧移情况;当从0.89继续增加时，曲线下降速度明显放缓，意味着继续增大局部刚度比对墙片的层间侧移影响已经不大，墙片Q1和Q3已处于相对安全的状态。因此，认为局部平均刚度比不宜低于0.89。

图6(b)中，实例模型中墙片Q1和Q3超越强度倍率达到2.0和1.6，墙体破坏严重。局部平均刚度比由0.47增加到0.70时，墙段超越强度倍率迅速降低，墙片的破坏状态得到明显改善。由于模型6和模型7中X向增加的刚度很大，因此墙段Q3最终达到完好和轻微破坏之间的状态。但是从整体上看，当局部平均刚度比大于0.70时，墙片破坏降低的趋势放缓，因此认为局部平均刚度比不小于0.7即可。

图6 墙片Q1和Q3计算结果Fig.6 Calculation results of wall piece Q1and Q3

2)Y向计算结果。

Y向与X向相比，变化趋势不明显，主要因为实例结构Y向上墙体较多、刚度较大，设计模型在Y向上局部平均刚度比增加幅度不明显。但从图7(a)的墙片Q2和图7(b)的墙片Q4可以看出，局部平均刚度比大于0.52时，曲线下降有一定放缓的趋势，低于0.52时，曲线斜率稍有增加，综合考虑认为局部平均刚度比不宜低于0.52。

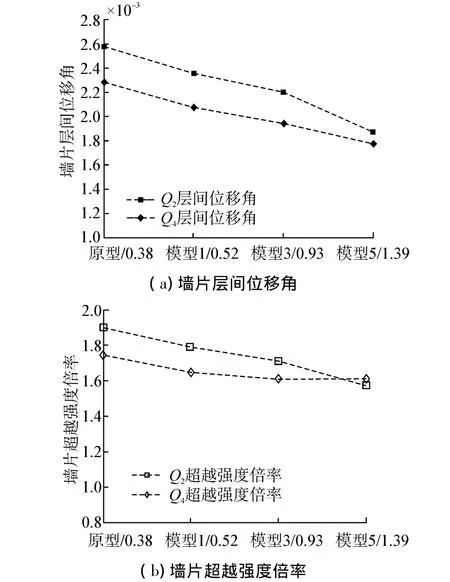
图7 墙片Q2和Q4计算结果Fig.7 Calculation results of wall piece Q2and Q4

3.2.2 区域B墙片计算结果

B区位于A区的对角线方向，分析区域A中局部刚度比的增加对区域B中墙体的影响，找出局部平均刚度比不宜高出的上限值。

1)X向计算结果。

图8(a)中，随着A区局部平均刚度比的增加，B区墙片的层间位移角均先减小后增加。曲线下降主要是A区刚度增加，使得整个楼层的总刚度提高，楼层整体侧移降低。但当A区的局部平均刚度比由1.46继续增大时，墙片Q5、Q6和Q7的层间位移角反而有所增加，原因为A区中局部刚度过强，造成楼层刚心向A区移动，B区逐渐成为远离刚心的部位，扭转增大;同时，A区局部平均刚度比过大，导致B区内的刚度相对不足，楼层薄弱部位转移到B区，造成墙片侧移有增大的趋势。因此认为A区的局部平均刚度比在达到1.46后不宜再继续增加，否则会对B区墙体产生不利影响。

图8(b)中，墙片Q5的曲线有先下降后上升的过程，分界点对应A区的局部平均刚度比为1.46;墙片Q6和Q7的超越强度倍率在局部平均刚度比由1.46增大到1.9的过程中几乎没有变化，当A区的局部平均刚度比进一步加大时，墙片Q6和Q7的破坏有加重的可能，但由于模型数量有限，未能描绘出这种趋势，为保守起见，局部平均刚度比的上限值取1.46和1.9的平均值，即认为A区的局部平均刚度比不宜大于1.68。

图8 墙片Q5、Q6和Q7计算结果Fig.8 Calculation results of wall piece Q5，Q6and Q7

2)Y向计算结果。

图9(a)中，墙片Q8和Q9的层间位移角有明显的先下降后上升的过程，对应的A区局部平均刚度比的临界点均为0.93;墙片Q10的曲线几乎呈一直线，说明对墙段Q10的影响不大，建议A区的局部平均刚度比不宜大于0.93即可。

图9(b)中，A区的局部平均刚度比超过0.93时，会加重墙片Q8的破坏程度;而墙片Q9在局部平均刚度比由0.52增大到1.39的过程中变化不大;墙片Q10的超越强度倍率呈下降趋势，但由于模型数量有限，未能找出曲线上升时对应的A区局部平均刚度比的临界点，为保守起见，局部平均刚度比的上限值取0.93和1.39的平均值，即认为A区的局部平均刚度比不宜大于1.16。

3.3 建议的局部平均刚度比的合理取值

由以上分析可知，局部平均刚度比不宜过低，否则会造成局部区域内抗侧刚度不足，墙体破坏严重，同时还会使整体楼层产生偏心距，加重结构的扭转效应;但局部平均刚度比又不宜盲目的提高，当某一区域内的局部平均刚度比过大时，虽然该区域内的墙体受力情况得到改善，但可能会造成薄弱部位转移，使得其他区域的墙体破坏加重。因此，结构的局部平均刚度比应该限制在一个合理的取值范围内，引导各道墙体均匀破坏。

通过对8个有限元模型中共计80道砌体墙片的计算分析，总结底框结构局部平均刚度比的建议合理取值范围:根据A区墙片的分析结果，建议下限值取0.89、0.52、0.7和0.52的平均值0.66;根据B区墙片的分析结果，建议上限值取1.46、1.68、0.93和1.16的平均值1.30，即底框结构局部平均刚度比宜控制在0.66～1.30。

图9 墙片Q8、Q9和Q10计算结果Fig.9 Calculation results of wall piece Q8，Q9and Q10

4 结论

1)底框结构震害实例中，底层破坏轻微、上部砌体层破坏严重的主要原因是:砌体层的楼层平面内刚度分布不均匀，局部有大开间，使得该区域内抗侧刚度不足;在其他墙体仅中等破坏的情况下，由于局部几道墙体破坏严重丧失承载力，导致整体结构无法继续正常使用。震害等级由中等破坏上升到严重破坏。

2)提出了局部平均刚度比的概念，作为衡量局部区域刚度的平均水平相对于整体刚度分布平均水平的参数指标。分析结果表明:局部平均刚度比过低则局部刚度不足，该区域内的墙体破坏严重;过高则局部刚度过大，造成薄弱部位转移，会对其他区域的墙体产生不利影响。建议底框结构的局部平均刚度比控制在0.66～1.30。

3)设计模型中A区中增加局部刚度的方法没有考虑使用功能的要求。在实际设计和施工中，建议采用增加墙体墙厚、提高砌块和砂浆的材料等级等方法对局部区域的刚度进行调整。由于文中的震害实例是汶川地震中出现的新的震害现象，类似的震害资料还比较少见，诸如场地类别、烈度大小等因素对取值的影响文中未做讨论，有关这一部分的研究内容将于后续的工作中展开。

［1］熊立红，高连军，熊朝晖，等.底框剪－砌体房屋抗震性能研究［J］.沈阳建筑大学学报:自然科学版，2008，24 (4):586-591.

XIONG Lihong，GAO Lianjun，XIONG Zhaohui，et al.Seismic performance of masonry building with RC framed lower floor［J］.Journal of Shenyang Jianzhu University:Natural Science，2008，24(4):586-591.

［2］刘砚山，童丽萍.抗侧刚度比对底框砌体房屋抗震性能的影响［J］.工程抗震与加固改造，2013，35(4):15-21，31.

LIU Yanshan，TONG Liping.Effect of lateral stiffness ratio on the seismic performance of bottom frame masonry structure［J］.Earthquake Resistant Engineering and Retrofitting，2013，35(4):15-21，31.

［3］韩夏.底层框架-抗震墙砌体房屋的抗侧刚度和抗剪强度控制问题研究［D］.重庆:重庆大学，2013:45-102.

HAN Xia.Research on the control of story lateral stiffness and shear strength for masonry buildings with frame and seismic-wall in first story［D］.Chongqing:Chongqing University，2013:45-102.

［4］中华人民共和国住房和城乡建设部.JGJ 248-2012，底部框架-抗震墙砌体房屋抗震技术规程［S］.北京:中国建筑工业出版社，2012.

［5］TUCKER C J.Predicting the in-plane capacity of masonry infilled frames［D］.Knoxville:The University of Tennessee，2007:52-79.

［6］刘红彪，刘现鹏，张强，等.底商多层砌体结构弹塑性地震反应计算方法［J］.建筑结构，2014，44(15):83-87.

LIU Hongbiao，LIU Xianpeng，ZHANG Qiang，et al.Calculation method of elasto-plastic seismic response of multi-story masonry structure with first floor used as shops［J］.Building Structure，2014，44(15):83-87.

［7］中华人民共和国住房和城乡建设部.GB 50010-2010，混凝土结构设计规范［S］.北京:中国建筑工业出版社，2010.

［8］刘桂秋.砌体结构基本受力性能的研究［D］.长沙:湖南大学，2005:13-38.

LIU Guiqiu.The research on the basic mechanical behavior of masonry structure［D］.Changsha:Hunan University，2005:13-38.

［9］叶列平，陆新征.汶川地震建筑震害分析［J］.建筑结构学报，2008，29(4):1-9.

YE Lieping，LU Xinzheng.Analysis on seismic damage of buildings in the Wenchuan earthquake［J］.Journal of Building Structure，2008，29(4):1-9.

［10］尹之潜，杨淑文.地震损失分析与设防标准［M］.北京:地震出版社，2004:88-92.