狭小间距间Cu/Al薄膜相互作用的分子动力学模拟

彭亚亚， 程广贵， 丁建宁,2， 凌智勇， 张忠强

(1. 江苏大学微纳米科学技术研究中心， 镇江 212013; 2. 常州大学低维材料及微纳米器件与系统中心， 常州 213164)

狭小间距间Cu/Al薄膜相互作用的分子动力学模拟

彭亚亚1， 程广贵1， 丁建宁1,2， 凌智勇1， 张忠强1

(1. 江苏大学微纳米科学技术研究中心， 镇江 212013; 2. 常州大学低维材料及微纳米器件与系统中心， 常州 213164)

采用分子动力学模拟软件基于Lennard-Jones-9-6势函数研究了狭小间距Cu/Al纳米薄膜间的相互作用. 我们通过计算薄膜表面单位面积上的范德华相互作用能，综合讨论了非接触Cu/Al薄膜间的相互作用. 结果表明，当两薄膜的间距从12 Å减小到3 Å时，相互作用能呈现两个阶段：起初几乎不变，然后迅速增大. 临界间距在7 Å附近. 在两薄膜相互靠近的过程中，相互作用能受体系尺寸、空位缺陷尺寸、表面涂层及薄膜间距的影响较大，然而几乎不受空位缺陷形状的影响.

纳米薄膜； 相互作用能； 分子动力学； 表面涂层； 范德华力

1 引 言

近年来，随着材料科学和微制造工艺的快速发展，薄膜广泛地应用在微/纳机电系统(Micro/nano-electro-mechanical systems, M/NEMS)来改变表面性能，如磁存储系统和微机电系统[1-3]. 由于微机电系统较大的表面与体积比，未接触的两物体间也存在着相互作用，如：范德华力[4]、微/纳米摩擦力[5]、量子力[6]及非接触摩擦力[7]等. Volokitin and Persson[8]计算了两表面相距1nm的范德华摩擦力，发现摩擦力的改善机制与不同表面谐振光子隧道效应有关.在谐振光子隧道处于低频表面等离子模式或吸附振荡模式时，范德华摩擦力能够提升七个数量级[9]. Stipeetal[10]第一次使用高灵敏度的镀金悬臂探测金针尖与Au(1 0 0)表面间的非接触相互作用，测出针尖阻尼是针尖与样品间距、温度和偏压的函数. Kuehnetal[11]观察了在不同高分子膜3—200nm上方镀铂悬臂针尖的运动轨迹，显示针尖的非接触摩擦力系数与高分子膜的介电属性有关. 许多在宏观尺度下可以忽略的相互作用(范德华力、量子效应、残余应力和静电力)在微观尺度下显得格外重要， 因为他们影响微机械的稳定性和性能. 因此，许多理论在微观尺度下不再适用，应用现有技术直接精确地探测分子效应仍很困难.

在众多理论模拟技术中，分子动力学由于其理论成熟和较高的计算效率，成为研究微观现象的一种重要工具[12].本文中，采用分子动力学模拟了不同纳米薄膜模型的相互作用.

本文通过分子动力学更加深入地研究体系尺寸、空位缺陷尺寸、空位缺陷形状、表面涂层和薄膜间距对相互作用的影响.观察这些属性间的联系，分析薄膜表面形貌.

2 模型和方法

采用Accelrys公司开发的Materials Studio 6.0中的Discover模块进行分子动力学模拟. 图1(a)、(b)和(c)分别是8-8层、6-6层和4-4层Cu/Al薄膜，以研究薄膜尺寸对两薄膜相互作用的影响. 在6-6层Cu/Al薄膜(图1(b))上进一步建立涂层、空位缺陷的模拟模型，在图1(b)中的模型上对温度进行研究.

为了消除周期性边界条件对分子动力学模拟过程的影响，研究中所使用的模型均在晶格参数为a=72.891Å，b=36.445Å和c=1000Å的周期性单元中[13]. 分子动力学过程中采用COMPASS[14](condensedphase optimized molecular potentials for atomistic simulation studies)力场来计算原子间的相互作用. 在COMPASS力场中采用Lennard-Jones-9-6势函数来计算两薄膜间的相互作用，其形式如下：

(1)

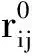
(2)

(3)

在所有的模拟过程中，截断半径均设置为9.5Å，选用正则系统NVT，通过Anderson[15]方法控制温度. 用Velocity-Verlet 算法对时间积分计算动力学过程，时间步长取1fs.

图1 初始间距为12 Å时，具有Cu(上方)和Si(下方)纳米薄膜表面的研究模型,(a)8-8层Cu/Al薄膜，(b)6-6层Cu/Al薄膜，(c)4-4层Cu/Al薄膜Fig.1 Models with copper (upward) and silicon (downward) nanofilms at the initial distance of 12 Å. (a) 8-8layers Cu/Al films, (b) 6-6layers Cu/Al films and (c) 4-4layers Cu/Al films

图2 温度为298K，间距为12Å时，(a)能量随模拟时间变化；(b)温度随模拟时间变化Fig.2 At the temperature of 298K and initial distance of 12Å, (a) the energy with simulation time; (b) the temperature with simulation time

对于所有的模型，动力学过程如下. 薄膜初始间距12 Å，两薄膜间为真空. 每进行完一次分子动力学计算后间距减小1Å，再进行分子动力学计算，重复以上步骤直到间距减小到3Å为止. 完全固定上层薄膜的最顶层原子和下层薄膜的最底层原子，其余中间原子自由弛豫. 为了更加接近真实情况，先在初始间距弛豫20ps使系统达到热平衡的稳定状态. 通过同时调整薄膜间距的减小量和步长获得具有一定速度的动力学过程. 用薄膜表面单位面积上的相互作用能表征表面间的相互作用强度. 公式如下：

σE=EInter/A=[Etotal-(Eupper+Elower)]/(a·b)

(4)

式中Etotal代表动力学过程后模型内的总能量，Eupper和Elower分别代表体系上层薄膜和下层薄膜在动力学过程后所具有的能量，a和b为晶胞参数a=72.891 Å，b=36.445 Å.

3 结果和讨论

研究模型在动力学时间20ps内是否能够达到平衡，可以根据模型内温度和能量是否收敛判. 图2是温度为298K，图1(b)所示模型在初始间距12Å时整个弛豫过程内温度和能量(包括势能和非键能)随模拟时间的变化过程. 由图2(a)、(b)可知，在运行动力学大约5000fs后，能量和温度都在恒定值附近小振幅波动. 这说明经过20ps后，研究模型内部温度和能量已趋于平衡状态[16].

研究中计算了距离从12Å到3Å时薄膜表面的相互作用能. 图3是温度为298K，具有不同模型尺寸的三组Cu/Al薄膜(分别为8-8层、6-6层和4-4层)在薄膜间距从12Å减少到3Å时的相互作用能变化. 从12Å到3Å变化过程中，相互作用能的变化分为两部分. 在两薄膜间距从12Å靠近到7Å之间，相互作用能几乎没有变化. 亦就是说，在12Å到7Å间相互作用能几乎不受体系尺寸的影响. 当薄膜间距低于7Å时，随着间距的减小，相互作用能急剧增加. 在3Å时，各模型的相互作用能从大到小依次为-3.428、-2.519和-1.922kcal·mol-1·Å-2. 薄膜尺寸越大，相互作用能越大. 这是因为体系尺寸越大，体系中的能量越高，所以相互作用就更剧烈.

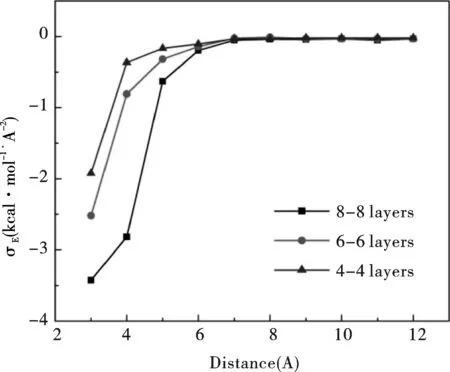
图3 温度为298K，不同薄膜尺寸下两表面间单位面积上相互作用能σE的变化Fig.3 At the temperature of 298K, interaction energy per unit area σE with different sizes of nanofilms

薄膜空位缺陷尺寸大小对非接触薄膜的相互作用影响较大. 在Cu薄膜中间分别建立三个方形空位缺陷，边长为8atoms、6atoms、4atoms，图4显示了不同空位尺寸对Cu/Al薄膜间相互作用能的影响.可以看出，当间距由12 Å减小到7 Å时，相互作用能变化不大且非常小，均在-0.037kcal·mol-1·Å-2附近变化.当间距减小到7 Å以下时，相互作用能急剧增大，且间距越小，作用能越大. 在3 Å时，相互作用能从大到小依次为-3.369、-2.896和-2.408kcal·mol-1·Å-2. 空位缺陷尺寸越大，相互作用能越小，即Cu/Al薄膜间相互作用强度越弱；反之，空位缺陷尺寸越小，相互作用能越大，即Cu/Al薄膜间相互作用强度越强. 由于上层Cu薄膜存在空位缺陷，在空位缺陷区域内没有Cu原子与下层薄膜上的Al原子相互作用，范德华相互作用相比无空位缺陷时减小. 空位缺陷尺寸越大，不参与相互作用的薄膜区域越大，范德华相互作用越弱；反之，空位缺陷尺寸越小，参与相互作用的薄膜区域越大，范德华相互作用越强.

图4 温度为298K，不同空位缺陷尺寸时单位面积上相互作用能σE的变化Fig.4 At the temperature of 298K, the interaction energy per unit area σE with different vacancy defect sizes

然而，从研究中可以发现，空位缺陷形状对薄膜相互作用几乎没有影响. 图5为Cu薄膜上面积相等而形状不同的三个空位缺陷对Cu/Al薄膜相互作用的模拟结果. 从图5可以看出，面积相等、形状不同的三个空位在间距从12 Å减小到3 Å时，相互作用能变化几乎相同. 由此可知，空位缺陷尺寸对Cu/Al薄膜的相互作用影响较大，而空位缺陷形状则对其几乎没有影响. 这是因为作用强度只与参与作用的原子数量有关，而与空位缺陷的拓扑结构无关. 不同空位缺陷形状的Cu薄膜，只要空位缺陷面积相等，参与作用的薄膜面积就相等，即参与相互作用的原子数量相等. 所以，相同面积、形状不同的空位缺陷对其薄膜相互作用几乎没有影响.

图5 温度为298K，不同空位缺陷形状时单位面积上相互作用能的变化Fig.5 At the temperature of 298K, interaction energy per unit area with different vacancy defect shapes

薄膜表面涂层对薄膜间相互作用能产生很大影响. 图6(a)分别是在Cu薄膜最底层和Al薄膜最顶层分别涂上一层Au原子和两层Au原子及无涂层时，相互作用能的变化情况. 间距在12 Å到7 Å时，相互作用能几乎不变. 在7 Å以下，没有Au涂层时Cu/Al薄膜间相互作用能增大相对平缓，而有Au涂层时相互作用能骤增，且Au涂层越厚，相互作用能越大. 图6(b)是Cu薄膜最底层和Al薄膜最顶层涂上一层Au、Ag及无涂层时，相互作用能的变化情况. 在作用间距小于7Å时，Cu/Al薄膜间涂Au的作用能明显比涂Ag时大，且均比没有涂层的Cu/Al薄膜间相互作用能大. 由此可知，薄膜间相互作用能不仅受表面涂层厚度的影响，还与涂层材料有关. 这是由于范德华力对吸收动量的低频激发极其敏感，因此与材料密切相关[17]. 金、银和铜相对原子质量大小关系为mAu>mAg>mCu，相互靠近的速度相同. 所以，动量大小关系为MAu>MAg>MCu. 动量越大，低频激发越强烈，范德华力越大，即薄膜间相互作用能越大.

图6 温度为298K，单位面积的相互作用能随(a)涂层厚度和(b)不同涂层材料的变化Fig.6 At the temperature 298K, the interaction energy per unit area with (a) coating thickness and (b) different materials of coating

图7 温度为298K，不同薄膜间距时镀金薄膜表面形貌的变化. (a) 3Å, (b) 6Å, (c) 7Å,(d) 10ÅFig.7 At 298K, changes of surface morforlogy of films with different distances. (a) 3Å, (b) 6Å, (c) 7Å and (d) 10Å

从前面的研究结果可知，狭小间距纳米薄膜间的相互作用能随着间距的变化而变化. 在12Å到7 Å时，相互作用能几乎不变. 然而，在低于7 Å时，随着间距的减小相互作用能迅速增大.在10Å时，薄膜变形较小，薄膜间作用强度较低，如图7(d). 间距减小到7Å时，薄膜变形仍然较小，薄膜相互作用强度与10Å时较接近，如图7(c). 当两薄膜间距减小到6Å时，如图7(b)所示，原子开始大面积塌陷，且上下两层薄膜出现粘附现象，薄膜变形较大，相互作用强度也较强. 由以上分析可知，两薄膜相互作用强度急剧变化的临界值为7Å.

从图7可知，随着间距的减小，薄膜间相互作用强度变强. 因为在一定间距范围内，范德华力与非接触薄膜间距d的三次方成反比(即Fvdw～1/d6). 在7 Å 以下时，d越大，范德华力越小，两薄膜间的相互作用越弱，薄膜变形较小；反之，d越小，范德华力越大，两薄膜间的相互作用越强，薄膜变形较大. 当d大到一定值时，范德华力趋近于零. 当薄膜间距小于7 Å时，由于所获得的范德华力具有吸引属性，上下两层薄膜由于较大的吸引力而出现粘附现象. 随着d减小，范德华力急剧增大，粘附现象更为严重，如图7(a)为d等于3Å时的粘附现象.

在3Å，两层薄膜表面塌陷严重，变形较大，薄膜间相互作用强度较强. 如图8所示，i层原子和i+1层原子的原子层间距满足关系式di+1>di(i=1,2,…,5 ). 由可知，i+1层原子的范德华力小于i层原子的范德华力，上层薄膜的作用强度自下而上减弱，下层薄膜的作用强度自上而下减弱.

图8 原子层间距d的示意图Fig.8 Sketch of atomic layer spacing d

4 结 论

通过分子动力学模拟研究狭小间距纳米薄膜间的相互作用. 主要研究了薄膜间距、体系尺寸、表面涂层及空位缺陷对相互靠近的非接触纳米薄膜相互作用的影响. 研究表明，体系尺寸、表面涂层及空位缺陷尺寸对非接触薄膜相互作用产生较大的影响，然而面积相等而形状不同的空位缺陷对其相互作用几乎没有影响. 薄膜临界距离处于7Å处. 研究中发现一些关于相互作用能的重要现象. 当薄膜间距从12Å减小到7Å过程中，相互作用能几乎不变；然而，在7Å以下时，随着间距的减小相互作用能迅速增大.

通过对分子动力学后的表面形貌分析，薄膜间距对其作用强度也有很大的影响. 从7Å减小到3Å过程中，狭小间距的纳米薄膜作用强度也随之增强.间距越小，薄膜变形越大，其相互作用强度越大. 上层薄膜的作用强度自下而上减弱，下层薄膜的作用强度自上而下减弱.

[1] Auciello O, Birrell J, Carlisle J A,etal. Materials science and fabrication processes for a new MEMS technology based on ultrananocrystalline diamond thin films [J]J.Phys.：Condens.Matt., 2004, 16(16)： 539.

[2] Radhakrishnan G, Adams P M, Speckman D M. Low temperature pulsed laser deposition of titanium carbide on bearing steels [J].ThinSolidFilms, 2000, 358(1-2)： 131.

[3] Hirayama T, Hishida N, Ishida H,etal. Performances of journal bearing with MoS2-shot coating for spindle of magnetic recording storage system [J].MicrosystTechnol., 2005, 11(8-10)： 751.

[4] Levitov L S. Van der Waals’ friction [J].Europhys.Lett., 1989, 8(6)： 499.

[5] Yoon E S, Singh R A, Oh H J,etal. The effect of contact area on nano/micro-scale friction [J].Wear, 2005, 259(7-12)： 1424.

[6] Lamoreaux S K. The experimental verification that a bizarre quantum effect-the Casimir force-can manifest itself in its repulsive form is pivotal not only for fundamental physics but also for nanotechnology [J].Nature, 2009, 457(8)： 156.

[7] Kohta S， Kenichi H， Yoshiyuki S，etal. Gigantic maximum of nanoscale noncontact friction [J].Phys.Rev.Lett., 2010, 105(23)： 236103.

[8] Volokitin A I, Persson B N J. Near-field radiative heat transfer and noncontact friction [J].Rev.Mod.Phys., 2007, 79(4)： 1291.

[9] Volokitin A I, Persson B N J. Non-contact friction between nanostructures [J].Phys.Rev. B, 2003, 68(15)： 155420.

[10] Stipe B C, Mamin H J, Stowe T D,etal. Noncontact friction and force fluctuations between closely spaced bodies [J].Phys.Rev.Lett., 200, 87(9)： 968011.

[11] Kuehn S, Marohn J A, Loring R F. Noncontact dielectric friction [J].J.Chem.Phys. B, 2006, 110(30)： 14525.

[12] Ong Z, Pop E. Molecular dynamics simulation of thermal boundary conductance between carbon nanotubes and SiO2[J].Phys.Rev. B, 2010, 81(15)： 155408.

[13] Makov G, Payne M C. Periodic boundary conditions in ab initio calculations [J].Phys.Rev. B, 1995, 51(7)： 4014.

[14] Sun H. COMPASS：An ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds [J].J.Phys.Chem. B, 1998, 102(38)： 7338.

[15] Andersen H C. Molecular dynamics simulations at constant pressure and/or temperature [J].J.Chem.Phys., 1980, 72(4)： 2384.

[16] Ma X F, Zhu W H, Xiao J J,etal. Molecular dynamics study of the structure and performance of simple and doubles bases propellants [J].J.Hazard.Mater., 2008, 156(1-3)： 201.

[17] Volokitin A I, Persson B N J. Adsorbate vibrational mode enhancement of radiative heat transfer and van der Waals friction [J].Surf.Sci., 2005, 587： 88.

Interaction between the closely spaced Cu/Al nanofilms based on molecular dynamics simulation

PENG Ya-Ya1, CHENG Guang-Gui1, DING Jian-Ning1,2, LING Zhi-Yong1, ZHANG Zhong-Qiang1

(1. Research Center of Micro/Nano Science and Technology, Jiangsu University, Zhenjiang 212013, China;2. Center of Low-Dimension Materials, Micro-Nano Device and System, Changzhou University, Changzhou 213164, China)

The interactions between the closely spaced Cu/Al nanofilms have been investigated by the molecular dynamics (MD) simulation based on Lennard-Jones-9-6 potential function. In this work, we performed a systematic evaluation on the interaction between the noncontact Cu/Al nanofilms by calculating van der Waals interaction energyper unit area on the surface of thin films. The results reveal that the interaction energy shows two stages：firstly keeps almost unchanged and then strengthens quickly when the distance between the two nanofilms decreases from 12 Å to 3 Å. The critical gap is found to be around 7 Å. Among normally approaching two nanofilms, the interaction energy is largely affected by system size, vacancy defects size, surface coatings and the distance between films. However, it is little affected by vacancy defects shape.

Nanofilms; Interaction energy; MD; Surface coating; Van der Waals forces

103969/j.issn.1000-0364.2015.02.026

2013-09-27

国家自然科学基金(50975130,51005103)

彭亚亚(1987—)，男，硕士，主要研究方向为非接触摩擦研究.E-mail： pengya584520@126.com

丁建宁. E-mail： dingjn@ujs.edu.cn

O56

A

1000-0364(2015)02-0323-06