波控中等潮差海滩剖面时空变化过程研究
于吉涛,丁圆婷,程璜鑫,陈子燊
(1.河南理工大学 测绘与国土信息工程学院,河南 焦作 454000;2.中国地质大学 环境学院,湖北 武汉 430074;3.中国地质大学 艺术与传媒学院 湖北 武汉 430074;4.中山大学 地理科学与规划学院,广东 广州 510275)
岬间海滩是全球岬角沉积海岸的一种重要地形,约占全球岸线的50%(Short et al,1999)。这些海滩在已有的文献中有不同的名字,比如:ζ 弯曲海滩、半心型海滩、对数螺线海滩、锯齿形海滩、弯状或钩状海滩、袋状海滩、岬间海滩和湾头滩等(Yu et al,2011)。海湾特征是:一弯曲遮蔽段,一稍微弯曲的过渡段和下游一相对顺直的切线段(如图1)。这类海滩是在长期斜向盛行涌浪作用而形成,是海湾不同岸段波、潮、风等动力因子与海滩地形相互作用的结果,不同岸段的海滩剖面的物质组成、坡度和地貌形态的时空变化性一定程度上反映了复杂的海滩地形动力过程。本文通过对粤西水东湾——一波控中等潮差海湾切线段布设的一海滩剖面16 个月重复观测获取海滩剖面数据,通过经验特征函数分析(EOF)剖面变化的主要空间特征及其物理意义,并对相对应的主要时间特征函数采用功率谱分析研究了主要剖面地形变化的时域特征。
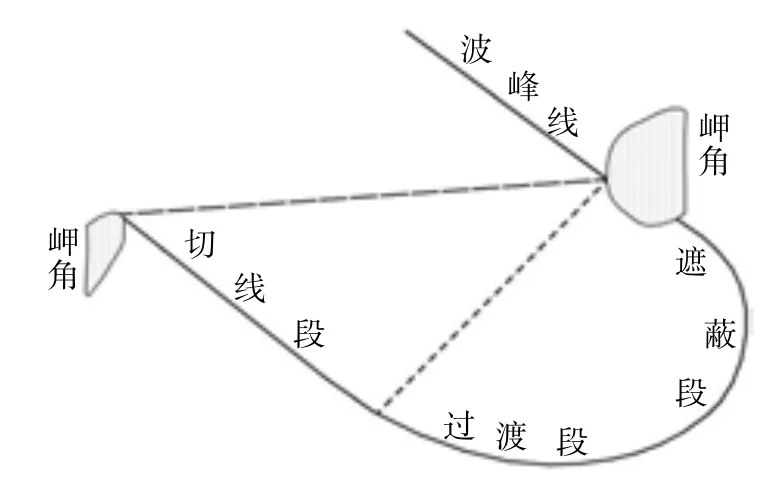
图1 岬间海滩形态结构
1 研究区概况
研究区位于广东省茂名市电白县境内,海岸由沙坝—泻湖—潮汐通道体系构成。沙坝长约9 km,走向大至呈北东—南西。沙坝分隔大海与泻湖于南北两面,留下一宽约1 km 的湾口成为泻湖与外海之间的潮汐通道。由于水深很小的巨大落潮三角洲对入射波的消能作用以及具射流性质的落潮流对入射波的阻抗,使得落潮三角洲具有堆积性“岬角”性质。受这个“岬角”屏蔽和晏镜岭下岬角的控制,湾口以西岸线平面上也构成了颇具特色的岬间海滩。研究岸段属于直线、开阔段,西接晏镜岭下岬角,东至晏镜村,海滩长约2 km(图2)。海滩高、中、低潮位附近表层泥沙由粗砂组成,平均粒径分别为0.73 mm、0.59 mm 和0.63 mm,分选系数分别为0.49、0.63 和0.55,反映了高潮位和低潮位很好的分选、中潮位好的分选。研究区常浪向ESE,夏季多SE 向和SSE 向浪。潮汐属于不正规半日潮类型,平均潮差1.75 m,平均大潮潮差2.6 m(陈子燊,2000)。按Davies(1964),研究区属波控中等潮差海区。
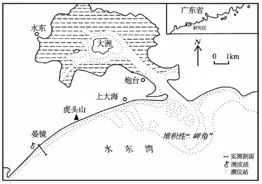
图2 研究区位置
2 数据预处理与研究方法
2.1 数据预处理
研究数据来自陈子燊(2000)数据,野外观测期间该处海滩未受到人类活动干扰,基本处于自然状态。对布设的这一条剖面,于每月大小潮期间进行测量,共获得68 条实测海滩剖面高程数据,观测时间16 个月。对每一条剖面水平距离等间隔分点(15 个高程点),得到相对于固定桩的距离(离岸距离)、绝对高程和海滩剖面图;对原来不等时间步长的68 条剖面时序采用样条函数以5d 等时序插值,得到96 条剖面(如图3)。数据插值的主要目的是对EOF 分析得到的时间特征函数可进行谱分析,产生的谱的峰值可用于识别空间特征函数的周期性变化。

图3 数据处理后96 条剖面形态图
2.2 经验正交函数
理解控制海滩时空变化的过程主要通过对海滩剖面连续数据包进行时空分解来实现,所采用的研究手段主要有经验正交函数(Winant et al,1975;Aubrey,1978,1979;Losada et al,1991;Medina et al,1994;Pruszak,1993;Larson et al,1999;Muñoz Pérez et al, 2001; Miller et al, 2007;Muñoz Pérez et al,2010)或小波理论(Li Y et al,2005;Reeve et al,2007)。自从Winant 等(1975)和Aubrey(1978)定义了海滩变化后,经验正交函数(Empirical Orthogonal Function,EOF) 方法已经被广泛应用于海岸地貌研究中,主要应用于海滩的垂岸变化(Winant et al,1975;Aubrey,1978,1979;Losada et al,1991;Medina et al,1994;Pruszak,1993;Larson et al,1999;Muñoz Pérez et al,2010) 和沿岸变化的研究(Muñoz Pérez et al,2001;Miller et al,2007)。作为一种广泛使用的统计工具,EOF 可被用于分析、确定海滩剖面随时间或海滩位置的变化,它是一种压缩型的研究剖面变化的方法,压缩的数据可确定变化的相对重要程度。通过变量分离的方法将数据y(x,t)中的时间和空间相关性分开,数据可以被一系列时间和空间函数的线性组合来代表(Davis,1986;Jackson,1991;Miller et al,2007):

其中,ek(x)为空间特征函数,ck(t)为时间特征函数或时间系数。通过k=1 到n 求和,n 是nx或nt中较小者,分别代表空间样本数和时间样本数。ak为标准化因子,(λk是第k 个特征函数的特征值),有时也会被并进ck(t)中。并要求特征函数满足:

δmn为克罗内克δ,即确保得到的特征函数是由一组统计上相互独立或不相关的向量所组成。特征函数以最小二乘法最优拟合数据,第一特征函数占据数据的大部分变化,随后的特征函数占剩余变化的大部分。结果以数据可能的最紧凑的形式表示,确保前几个特征函数占据最重要的变化。在数学上采用拉格朗日乘数法规范这一要求:
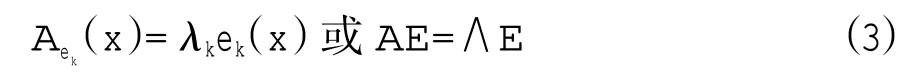
E 为空间特征函数矩阵,ek(x)和∧为特征值λk组成的三角矩阵。对矩阵A,本文采用交叉矩阵进行计算:

Y 是由y(x,t)的单独要素组成,YT是Y 的转置阵,方括号中的项代表矩阵A 的维数。当空间特征函数ek(x)被确定后,时间特征函数的求解可采用类似空间特征函数的计算步骤:

矩阵B 给出了y(x,t)时间协方差的测度,矩阵A 给出了y(x, t) 空间协方差的测度。如公式(5)和(6)所示,[nt,nt]为矩阵B 的维数,C 包含时间特征函数ck(t)。公式(4)和(6)的比较指示了矩阵A 和B 有不同的维数,因此二者方程中∧的计算也是不同的维数。
当给出矩阵A 和B 的定义,矩阵的迹或对角元素之和必须等于数据的均方值。方程(3) 和(5)也反映了矩阵的特征值之和必须等于数据的均方值,每一个单独的特征值λk代表了模态k 占总变化的相对贡献量,那么pk的计算为:

前几个模态将包含数据中的大部分的变化量,即EOF 能把数据中有意义的主要信号与较低模态中的噪音区分开。而对于每一对联合特征函数yk(x,t)=akck(t)ek(x),则可基于一个预设的水平L 重构原始数据。即:

通常基于方差阈值指定L,代表最小数量变化的模态被认为是噪音,可被滤除,即重构过程具有滤波功能。另外,由于单独的ek(x)和ck(t)常常比较抽象,而yk(x,t)所代表的联合特征函数由于更容易被理解,也是很有用的。
3 结果与讨论
通过3.1 数据预处理得到96×15 剖面高程数据(图3),分别计算这一数据的平均剖面、极差与标准差(图4),然后对这一数据进行EOF 分析(图5、图6)。注意在对剖面高程数据做EOF 分析时,本文对这一数据进行了距平处理。如果没有对数据去平均,第一空间特征函数e1(x)将明显与统计平均值密切相关,将占剖面总变化的98.76%,指示的是平均海滩函数,这一结果已经被Winant 等(1975)和Miller 等(2007)所证实。本文通过对数据去平均,提取了占数据总方差91.32%的前3个空间特征函数来研究海滩剖面的空间变化(表1、图5),并对相对应的前3 个时间特征函数(图6)作连续功率谱估计及检验(图7),以识别这一海滩剖面变化的时间特性。

表1 前4 个特征函数所代表的总变化(pk)的百分比

图4 剖面的平均值、极差和标准差
图4 所示的平均剖面从岸上向水下呈现出一个相对平稳的线性趋势,极差与平均岸线趋势相似,结合图3 可看到平均水面位置有约10 m 的活动范围,反映了潮汐水面对平均水平面的平移作用;标准差从岸线0 位置向离岸30 m 处,呈逐渐线性增加的趋势,表明剖面变动逐渐加剧;离岸30 m 到50 m 处标准差呈线性减小的趋势,表明剖面变动相对前一位置逐渐减弱;离岸50~70 m 处标准差又呈线性增加的趋势,表明剖面变动进一步加剧。平均剖面、极差和标准差基本指示了该处海滩低潮带附近及滩肩位置较强烈的剖面变动特征。

图5 EOF 分析后得到的前3 个空间特征函数e1(x)- e3(x)

图6 EOF 分析后得到的前3 个时间特征函数c1(t)-c3(t)

图7 前3 个空间特征函数e(1x)-e(3x)对应的前三个时间特征函数c(1t)-c(3t)的各自功率谱
空间特征函数的极值表示最大变化的区域,而节点指示的是相对稳定的地带,在节点处发生泥沙交换,可将毗邻区域的淤积和侵蚀划分开,因此剖面变化在结点两侧呈现反相。由图5,第一空间特征函数e1(x)占总方差的49.85%,是海滩剖面变化最主要的模式。在离岸约12 m 和20 m 处存在节点,表明了该处泥沙的输运,但是离岸0~25 m 的剖面变动相对稳定,指示了后滨相对稳定的特征;从离岸距离30~70 m 甚至更远剖面变动逐渐增大,指示了滩肩顶至碎波带海滩剖面变动逐渐增强的特征,反映了泥沙沿剖面的横向往复运动,且沿着滩面向下泥沙变动逐渐增强,这是整个剖面形成和变化最主要的特征。从图8 联合特征函数图中也可以看出,从离岸距离30~70 m 剖面的空间变化幅度为稳定的增加,体现了剖面变化的线性模式。对与第一空间特征函数e1(x)相对应的第一时间特征函数c1(t)(图6)作连续功率谱分析,图7(a)中的红线代表置信水平95%的红噪音理论检验谱,可发现第一时间特征函数的连续功率谱在波数16 处显著,对应15 d 的显著周期。反映了该海滩剖面波能在大、小潮汐约半月潮周期内对该过程的控制。这一从滩肩顶到中潮带逐渐增加的状态,表明了沿滩面向下的泥沙输运是在第一个大潮间隔期间发生的。这时,冲流抵达,偶尔会越顶,滩肩顶处于连续的高潮下。当潮汐降为小潮时,海滩开始恢复,当经过下一个较低的大潮间隔时,泥沙被推回滩面。在下一个小潮间隔后随着潮差增加到大潮,泥沙将沿滩面向下运动。这是最主要的海滩响应。
第二空间特征函数e2(x)占总方差的30.96%,是海滩剖面变动的次要模式。由图5 可看出在离岸0~15 m 处剖面变动相对平稳,指示了相对稳定的后滨环境;自离岸15~30 m 处剖面变动逐渐增大,且在离岸30 m 出现极大负值,对应于滩肩向海端,在离岸约55 m 处出现结点,结点两侧呈反相,反映了高潮带至上冲流作用上限之间剖面变动的主要特征,代表了滩肩的形成和消亡过程,是海滩剖面水上部分最主要的过程,为冲流带函数模态,从图8 联合特征函数图可更好的反映出滩肩的形成与消亡。对与第二空间特征函数e2(x)相对应的第二时间特征函数c2(t)作连续功率谱如图图7(b),可发现这一冲流函数模态的连续功率谱在波数10、11 处显著,对应24~21.8 d 的显著周期。这一冲流模态表明了沿着海滩的泥沙输运有大约近塑望月潮频率的周期。这一结果与Clarke 等(1984)的结果是一致的。随着潮差的增加,剖面的上部将被冲流带和碎波带过程控制,较低的部分被波浪浅化过程所控制。实际上,高潮位以上滩肩地形的发展是和低潮位以下沙坝体系的动态密切相关的,若沙坝体系向岸迁移而且连接到滩面后,滩面坡度减小,海滩剖面为恢复粒级与波能之间的平衡关系,通过冲流过程,特别是高潮时的冲流作用把滩面泥沙向上搬运和堆积,此时波浪强度的波动又易使上冲泥沙越过滩肩脊堆积在滩肩顶面上,滩肩向上增长,并可能形成向岸倾斜的滩面连接面。随着滩肩增长,滩面坡度增大,剖面将重新趋向平衡。

图8 EOF 分析得到的前3 个联合特征函数
第三空间特征函数e3(x)占总方差的10.51%,由图5 可看出从离岸0~25 m 剖面变动逐渐加强,且在离岸25 m 处出现极大正值;在离岸30 m 出现结点,结点两侧反相,在离岸30~40 m,剖面变动又逐渐增强,且在离岸40 m 出现极大负值,但绝对值低于极大正值,在离岸55 m 附近出现结点,结点两侧反相。第三空间特征函数e3(x)主要体现了中潮带上部滩面的波动特征,地形上对应于大潮高潮位的巨型滩角。Short(1991)提出,上涨的潮汐和入射波将相互作用而能是剖面维持,在高潮时将易于形成次谐边缘波。长重力波的产生也将被上涨的、更高的潮汐所支持,但是,变化的水面可能将抑制它们对海滩下部地形的影响。在所有海滩系统中,高潮冲流带可看到形成的滩角,存在中等到较高能量的大潮海滩系统中(Short,1991)。尽管对于滩角成因的研究有不同的看法,但野外观测表明,这种高潮滩角的形成明显地与大浪及大潮动力条件是联系在一起的,由图8 联合特征函数图可以直观的显示韵律地形的存在。对与第三空间特征函数e3(x)相对应的第三时间特征函数c3(t)作连续功率谱如图图7(c),可发现第三时间特征函数的连续功率谱在波数4、5、6 显著,对应60~40 d 的显著周期。反映了这一滩角地貌在大、小潮汐约2个月潮周期内对该过程的控制。
4 结论
本文通过对粤西水东湾——波控中等潮差海滩剖面数据进行研究,发现该段海滩整体表现出切线段海滩整体表现出低潮带附近及滩肩位置较强烈的剖面变动特征,这一特征为平均海滩函数。通过EOF 分析,提取占矩阵总方差91.32%的前3 个空间特征函数研究海滩剖面空间变化,发现:(1)第一空间特征函数e1(x)占总方差的49.85%,是海滩剖面变化最主要的模式。指示了滩肩顶至碎波带海滩剖面变动逐渐增强的特征,体现了海滩剖面的线性变化模式;(2)第二空间特征函数e2(x)占总方差的30.96%,指示了该处海滩滩肩的形成与消亡过程,这一特征为冲流带函数模态;(3)第三空间特征函数e3(x)占总方差的10.51%,指示了韵律地形的存在,对应着大潮高潮位的巨型滩角地形。
通过对这3 个空间特征函数相对应的时间特征函数作连续功率谱分析,发现这3 个空间变化过程分别有约15 d、24~21.8 d、60~40 d 的周期,反映了该海滩剖面波能在大小潮汐约半月潮周期、近塑望月潮频率周期和大小潮汐约2 个月潮周期内对这些空间过程的控制,体现了这一波控中等潮差海岸叠加在周期性潮汐之上的波浪作用使海滩演变的主要动力因素,这在以前的研究中(陈子燊等,1990;陈子燊等,1991;陈子燊,2000)所忽略。
Aubrey D G, 1978. Statistical and Dynamical Prediction of Changes in Natural Sand Beach,Ph D thesis,Scripps Institution of Oceanography,San Diego,194.
Aubrey D G, 1979. Seasonal Patterns of Onshore/Offshore Sediment Movement.Journal of Physical Research,84(C10):6347-6354.
Clarke D J,Eliot I G,Frew J R,1984.Variation in subaerial beach sediment volume on a small sandy beach over a monthly lunar tidal cycle.Marine Geology,58:319-344.
Davies J L, 1964. A morphogenetic approach to world shorelines.Zeitschrift für Geomorphologie,8:127-142.
Davis J C, 1986. Statistics and Data Analysis in Geology. John Wiley &Sons,Inc,New York,NY.
Jackson J E, 1991.A User's Guide to Principal Components. John Wiley&Sons,Inc,New York,NY.
Larson M, Hanson H, Kraus N C, et al, 1999. Short and long term responses of beach fills determined by EOF analysis. Journal of Waterway,Port,Coastal and Ocean Engineering,125(6):285-293.
Li Y,Lark M,Reeve D,2005.Multi-scale variability of beach profiles at Duck:A wavelet analysis.Coastal Engineering,52:1133-1153.
Losada M A, Medina R, Vidal C, et al, 1991. Historical evolution and morphological analysis of El Puntal spit,Santander (Spain).Journal of Coastal Research,7:711-722.
Medina R,Losada M A,Losada I J,et al,1994.Temporal and spatial relationship between sediment grain size and beach profile. Marine Geology,118:195-206.
Miller J K,Dean R G,2007.Shoreline variability via empirical orthogonal function analysis:Part 1 temporal and spatial characteristics.Coastal Engineering,54:111-113.
Muñoz Pérez J J,Medina R, Tejedor B,2001.Determination of longshore variations by EOF method in Victoria Beach (SW Spain). Scientia Marina,65(4):393-402.
Muñoz Pérez J J, Medina R, 2010. Comparison of long-, medium- and short-term variations of beach profiles with and without submerged geological control.Coastal Engineering,57:214-251.
Pruszak Z, 1993. The analysis of beach profile ch anges using Dean's method and Empirical Orthogonal Functions. Coastal Engineering,19:245-261.
Reeve D,Li Y,Lark M,Simonds D,2007.An investigation of the multiscale temporal variability of beach profiles at Duck using wavelet packet transforms.Coastal Engineering,54:401-415.
Short A D, 1991. Macro -Meso Tidal Beach Morphodynamics—An Overview.Journal of Coastal Research,7(2):417-436.
Short A D, Masselink G, 1999. Embayed and structurally controlled beaches.In:Short,A D (Ed.),Handbook of Beach and Shoreface Morphodynamics.Wiley,New York,230-249.S
Winant C D, Inman D L, Nordstrom C E, 1975. Description of Seasonal Beach changes Using Empirical Eigenfunction.Journal of geophysical Research,80(15):1979-1986.
YU Ji-tao, CHEN Zi-shen, 2011. Study on Headland-Bay Sandy Coast Stability in South China Coasts.China Ocean Engineering,25(1):1-13.
陈子燊,李春初,1990.弧形海岸中间过渡带海滩剖面的地貌动态分析.海洋科学,2:6-12.
陈子燊,李春初,罗章仁,1991.广东水东湾弧形海岸切线段海滩剖面的过程分析.海洋学报,13(1):82-90.
陈子燊,2000.海滩剖面时空变化过程分析.海洋通报,19(2):42-48.

