一种适用于深海长基线定位的自适应分层声线跟踪法
李圣雪,王振杰,聂志喜,王毅,吴绍玉
(1.中国石油大学(华东),山东 青岛 266580;2.中国石油东方地球物理公司,河北 涿州 072751)
声波在海水中的传播方向会随着声速的变化而变化从而产生折射,这导致声线轨迹不再是一条直线(赵建虎等,2008;孙革,2007)。如果采用固定的声速计算,会带来很大的误差(齐娜等,2003)。为了提高精度,需要对声线轨迹进行修正(王燕等,2009)。因此声线跟踪技术(何高文,2000;朱小辰,2011;蔡艳辉,2013)被应用到水声定位领域。声线跟踪技术利用分层近似、逐层计算的方法对声线弯曲进行补偿,从而改善定位精度(张居成,2013;Yang et al,2011)。分层等梯度的声线跟踪方法是常用的一种声线修正方法(刘伯胜,1997;Takahashi et al,2000),该方法假设层间声速等梯度变化,采用逐层计算获取的声线轨迹与真实声线轨迹最为接近,精度较高(葛亮,2006)。但在深海区域运用此方法定位时,定位效率会因为声速层数过多而大大下降。本文提出了声速剖面(李胜全,2001) 的自适应分层方法,将梯度变化较小的层进行合并,保留梯度变化较大的声速层,减少迭代计算层数,在保证精度的情况下显著地提高了运算速度。本文方法与张居成(2013)方法相比,原理更为简单,实现更为方便。
1 分层等梯度声线修正法
声波在海水中的传播遵循Snell 法则(张红梅,2010;丁继胜,2005)

式中:θ 为声线入射角,C 为声速,P 为Snell 常数。
分层等梯度声线跟踪方法假设声波经历的水柱分为N 个等梯度层,即声波在每层的传播速度是等梯度的。在水深为zi的i 层,分别用Ci和θi表示声波的传播速度和入射角度(图1)。第i 层内的声速梯度gi可用下式表示

式中:Δzi为第层的水层厚度,Ci+1为第i+1 层声速。
由于声波的传播满足Snell 法则,在声速常梯度变化的情况下,波束在第i 层内的实际传播轨迹为一连续的、对应一定曲率半径Ri的弧段(陆秀平,2012;赵建虎,2002),Ri的表达式如下

层i 内声线的水平位移(兰华林,2007)为

式中:θi为第i 层声线的入射角,θi+1为第i+1 层声线的入射角。
波束在该层经历的弧段长度为

则经历该段的时间为
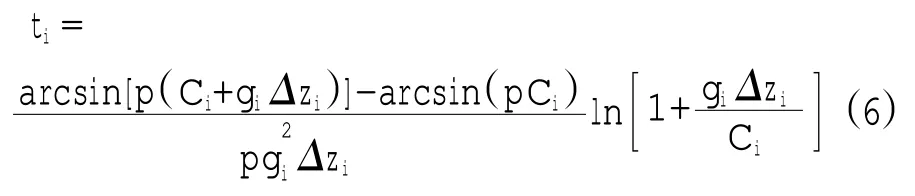
此种方法跟踪的声线路径与真实声线吻合,计算精度相对较高,但当数据层数较多时,迭代耗时,运算量大。
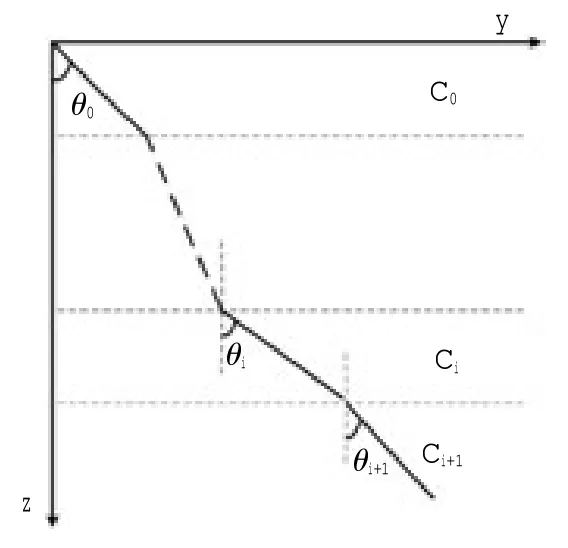
图1 分层等梯度声线跟踪示意图
2 自适应分层声线跟踪法
为了解决深海高精度定位运算量过大、定位效率低的问题,提出了自适应分层声线跟踪的方法。该方法的思想是通过对声速剖面数据进行合理抽稀并保留信息量多的声速层,在满足定位精度需求的前提下减少定位耗时。声速剖面自适应分层原理如图2 所示。
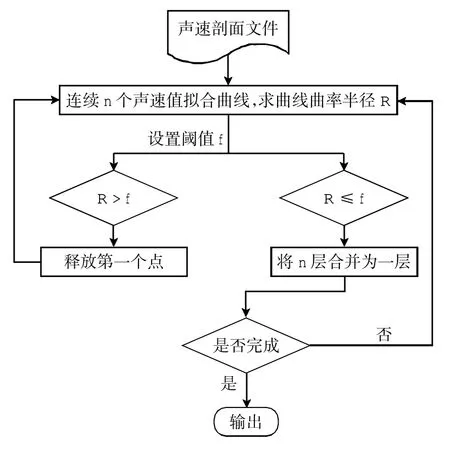
图2 自适应分层原理图
首先,设定合理的拟合窗口大小n,n 值取值过小会造成拟合多项式的参数不准确,n 值取值过大会造成拟合后层数过少。然后,从顶层开始选取连续的n 个声速值Ci(i=1,2,…,n)进行曲线拟合。对于拟合的曲线求其最大曲率,曲率计算公式为

如果曲率小于等于设定的阈值,则将此n 层声速值合并为一层;如果曲率大于设定的阈值(表明此数据中声速剖面变化较大),则此n 层不能合并为一层,释放n 个点中的第一个点,下移一个点继续选取n 个点声速值进行拟合。通过此方法将声速剖面数据中变化很小的声速层进行过滤,适当抽稀,保留声速梯度变化较大的数据层,从而减少迭代中的运算量。
声速剖面经过自适应分层后,用新的声速剖面进行分层等梯度声线跟踪,从而完成水下定位解算。
3 仿真算例及结果分析

图3 水域声速剖面图
根据声速剖面数据(如图3 所示,其中(a)数据为中国南海声速剖面数据(Yang et al,2011),(b)为中国Argo 浮标数据(中国Argo 网站))进行浮标位置及声波传播时间数据模拟。利用自适应分层的声速剖面将模拟的浮标定位数据进行解算,计算水下应答器的位置。定位模型为圆曲线模型,解算的方法为王燕等(2002)的分层等梯度声线修正方法,坐标满足要求时可结束迭代,获取水下应答器的位置信息。将获得应答器坐标与模拟坐标真值进行比对,求得真误差,检验自适应分层声线跟踪方法的效果。
3.1 仿真算例1-500 m 水深实验
如图4,模拟4 个浮标布设成正方形形状,边长为1 600 m,给浮标的三维坐标分别加上2 m 的余弦波动。海底模拟4 个应答器A、B、C、D,坐标分别为(0,0,-500)、 (0,40,-500)、(40,0,-500)、(40,40,-500),单位均为m。总共模拟100 个历元,浮标100 历元位置放大如图5 所示。水域的声速剖面图如图3(a),采样间隔为1 m。误差模拟如下:换能器定位中误差x、y、z 方向各10 cm,应答器时延偏差为8 cm 的系统误差,测量时间造成10 cm 的测距中误差。
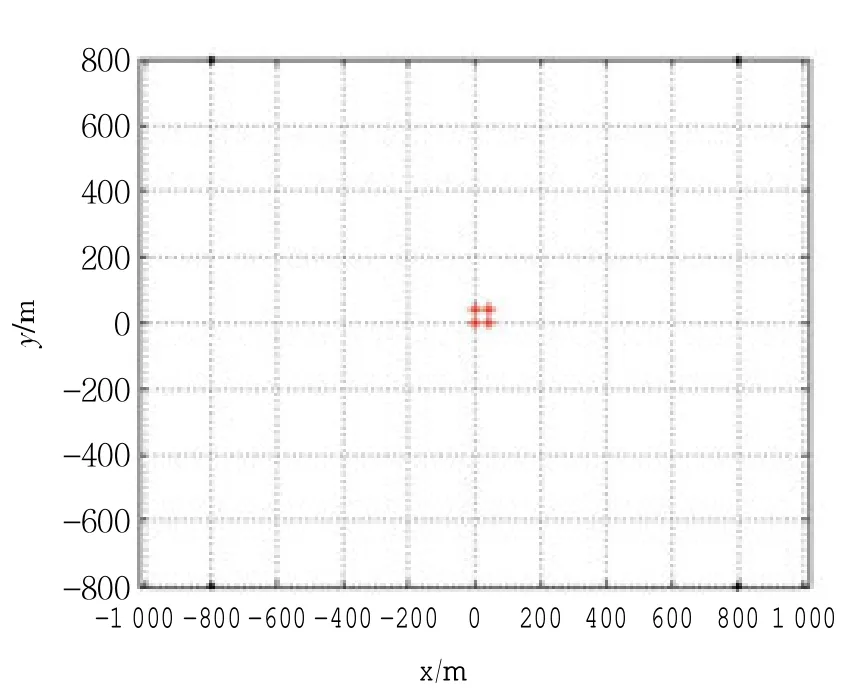
图4 数据模拟示意图
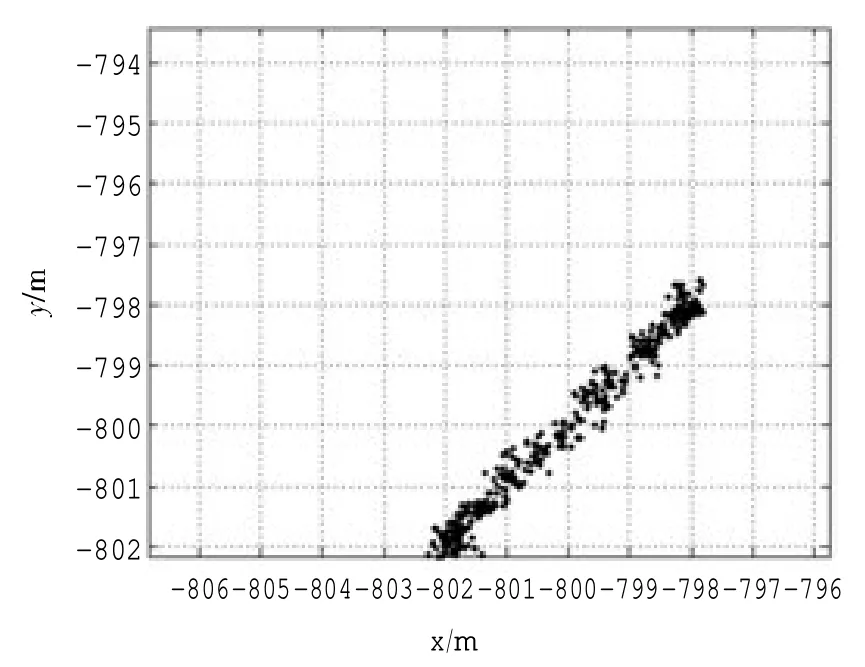
图5 浮标100 历元位置示意图
为了进行对比,首先用原始声速剖面(500层)对水下4 个应答器进行定位,4 个应答器定位结果见表1:
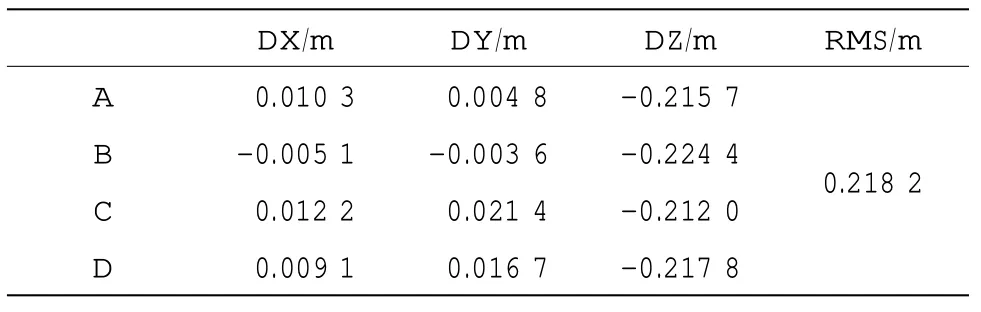
表1 500 m 数据分层等梯度声线跟踪定位误差
实验中的电脑配置为:CPU 型号为双核Pentium E2200,CPU 主频为2.20 GHz,内存大小为3G。用原始的声速剖面定位,需要26.742 s,从表1 可以看出,水平方向的定位误差最大为2 cm,最小为4 mm,定位精度为毫米级到厘米级,垂直方向的定位误差在20 cm 左右,定位精度为分米级,RMS 值为0.218 2 m。
对声速剖面进行自适应分层,为了测试阈值对定位结果的影响,实验中阈值选取为10-1,10-2,10-3……,10-20,共20 个阈值,拟合点数n 设置为7,拟合曲线设置为三次多项式拟合,即每7 个数据点进行三次多项式拟合。
图6 所示阈值为10-1与10-20时声速剖面分层结果对比图,可以看出阈值越大,层数越少。对于原始数据,均能进行不同程度的抽稀。

图6 不同阈值时声速剖面分层结果图
利用上述11 个阈值得到的自适应分层声速剖面数据进行分层等梯度声线跟踪定位水下4 个应答器的位置,计算结果见表2:
从表2 结果中可以看出,不同的阈值,对声速剖面有不同程度的抽稀,层数从145 层到450 层,其中,阈值从10-1到10-12分层结果一致,均为145 层。定位的时间从不到7 s 到近24 s,定位的效率较原始结果有了不同幅度的提升。定位的精度方面:平面位置定位结果差别很小,误差最大在2cm左右,最小不足4 mm。高程定位误差在20 cm 左右,与原始定位误差接近,不同阈值定位误差差异很小。对于不同的阈值,其定位RMS 值均在0.22左右,相差不大,与未经过自适应分层的定位结果相当。图7 为对于不同阈值的自适应分层定位结果水平方向RMS 和垂直方向RMS 的对比结果,可以看出不同阈值定位结果水平方向RMS 基本一致,垂直方向RMS 值区别不大,差别为毫米级。
3.2 仿真算例2-1 000 m 水深实验
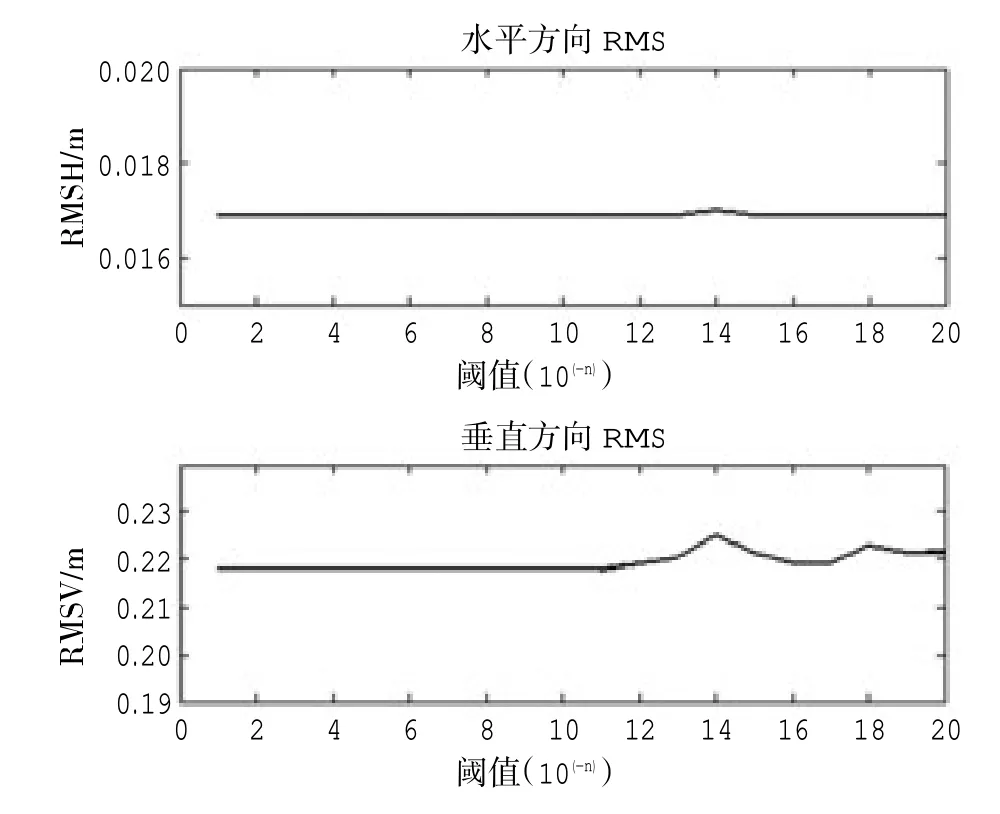
图7 500 m 仿真数据不同阈值定位结果水平方向RMS 和垂直方向RMS 对比
模拟4 个浮标布设成正方形形状,边长为2 400 m,给浮标的三维坐标分别加上2 m 的余弦波动。海底模拟4 个应答器A、B、C、D,坐标分别为(0,0,-1 000)、(0,100,-1 000)、(100,0,-1 000)、(100,100,-1 000),单位均为m。总共模拟100 个历元,水域的声速剖面图如图3(b),采样间隔为1 m。误差模拟如下:换能器定位中误差x、y、z 方向各10 cm,应答器时延偏差为8 cm 的系统误差,测量时间造成10 cm 的测距中误差。
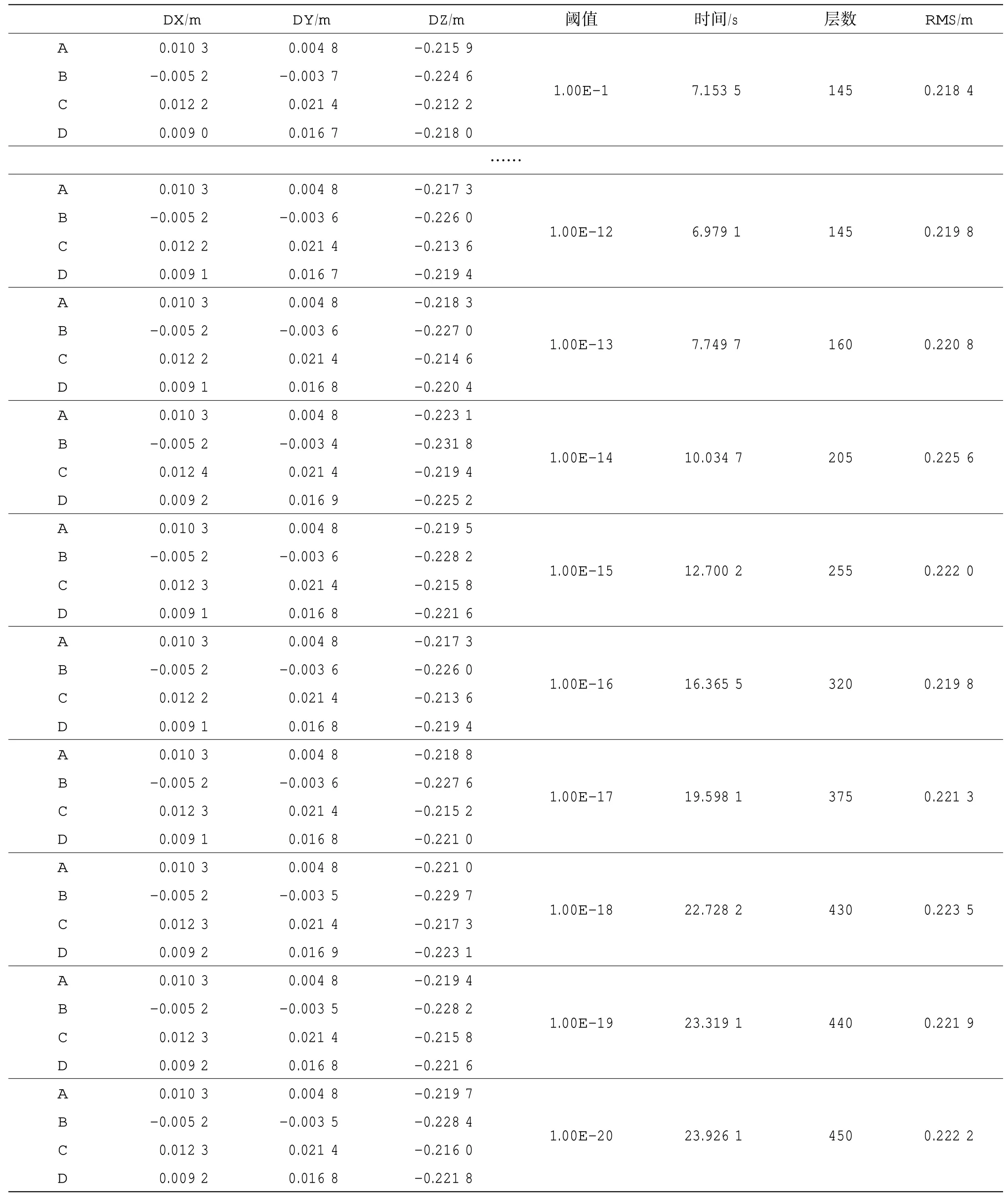
表2 500 m 仿真数据不同阈值水下定位误差
首先,用原始声速剖面(1 000 层)对水下应答器位置进行定位,结果如表3:
用原始的声速剖面定位,需要的计算时间为41.272 5 s,从表3 结果可以看出,水平方向的定位误差最大为2.26 cm,最小为3.7 mm,定位精度为毫米级到厘米级,垂直方向的定位误差少于20cm,定位精度为分米级,定位的RMS 值为0.180 1 m。
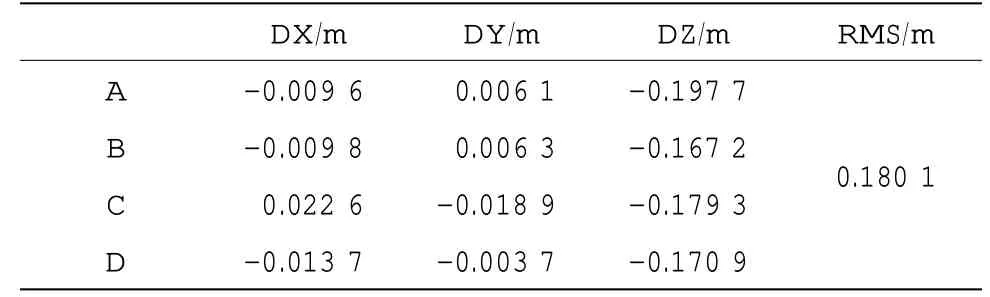
表3 1 000 m 数据分层等梯度声线跟踪定位误差
利用新提出的自适应分层声线跟踪方法对水下应答器进行定位,20 个阈值定位结果如(下页)表4:
从表4 中看出声速剖面经过自适应分层后变化为从285 到730 层不等,阈值从10-1到10-10分层结果一样,均为285 层。定位时间也从10 s 到34 s不等,定位的误差与用原始声速剖面定位的误差相当,水平位置误差最大不超过3 cm,最小不到2 mm,高程方向误差基本不超过20 cm。对不同的阈值,定位RMS 值差别不大,与未经过自适应分层的定位结果相当。
图8 为对于不同阈值的自适应分层定位结果水平方向RMS 和垂直方向RMS 的对比结果,可以看出不同阈值定位结果水平方向RMS 基本一致,垂直方向RMS 值区别不大,差别为毫米级。
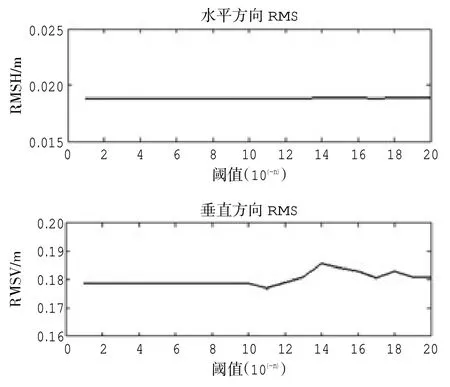
图8 1 000 m 仿真数据不同阈值定位结果水平方向RMS 和垂直方向RMS 对比
从两组实验结果可以看出,对于不同的水深,不同的声速剖面数据,提出的自适应分层声线跟踪方法均能有效地减少运行时间,在保证定位精度的前提下大大提高定位的效率。对比不同阈值的结果,在满足需要的情况下可以设置较大阈值,保留主要信息层,提高定位效率。阈值的确定可以根据实际声速剖面情况而定,试验中可看出阈值为10-10即可满足要求。
4 结论
本文针对提高深海声学定位中分层等梯度声线跟踪定位的效率问题,提出了自适应分层声线跟踪的方法,得到如下结论:
(1)所研究的自适应分层声线跟踪方法可对声速剖面数据进行合理分层,根据阈值大小保留必要的声速层,在保证定位精度的前提下减少了迭代计算的时间,与传统方法相比,明显地提高定位效率,在深海水下导航定位中有较好的应用前景。
(2)分层阈值的选择是一个值得研究的重要问题,本文采用的是实验结果,关于阈值的自动选取方法还需要进一步深入研究。
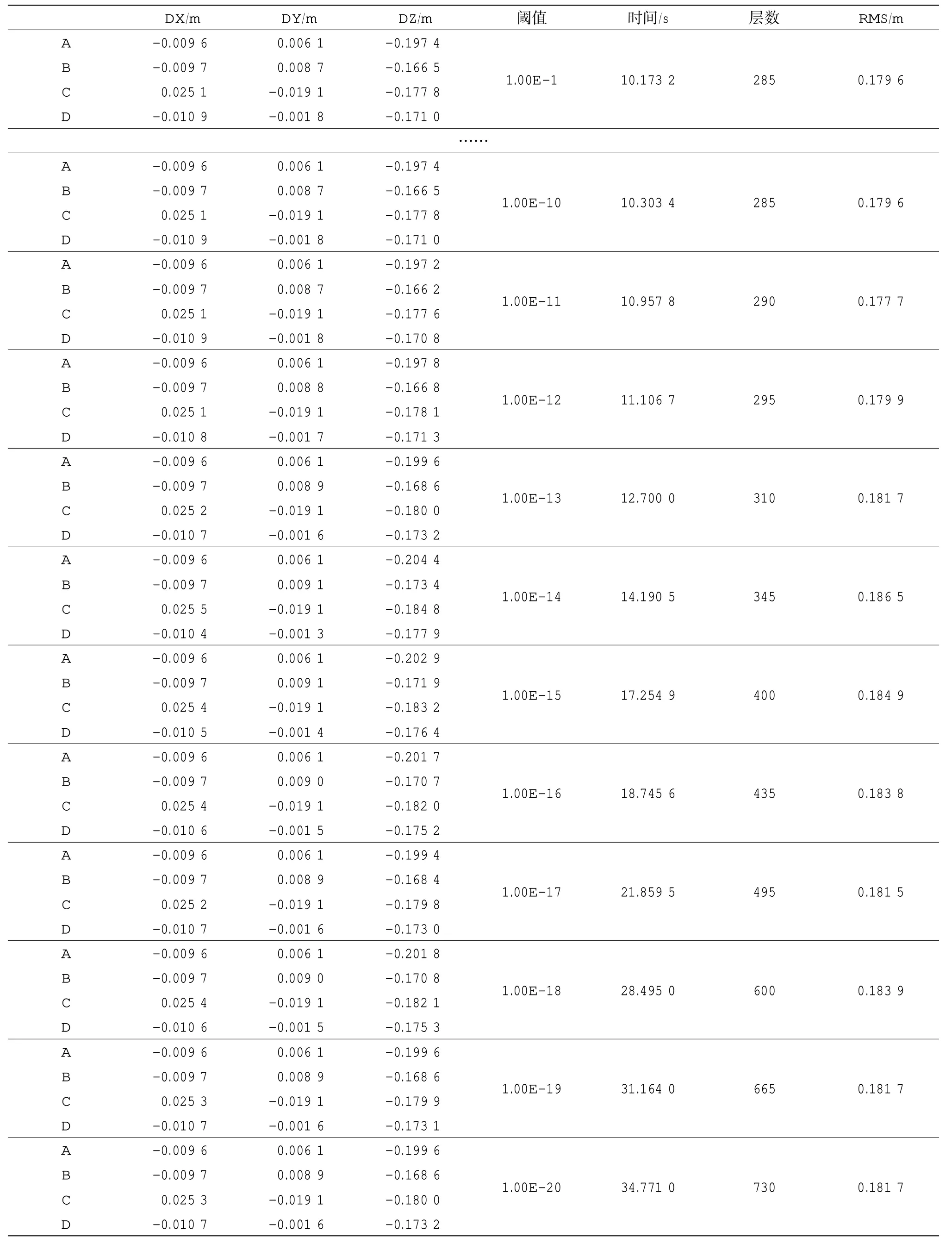
表4 1 000 m 仿真数据不同阈值的水下定位误差
Takahashi N,Futa K,Tsuchiya T,et al,2000.Calculation of eigenray with equi-sound -speed division of sound speed profile. Acoustical Science and Technology,21(3):153-161.
Yang F, Lu X, Li J, et al, 2011. Precise positioning of underwater static objects without sound speed Profile. Marine Geodesy,34 (2): 138-151.
蔡艳辉,程鹏飞,2013.表层海水中声纳定位的声速问题.遥感信息,(6):3-9.
丁继胜,周兴华,唐秋华,等,2005.基于等效声速剖面法的多波束测深系统声线折射改正技术.海洋测绘,24(6):27-29.
葛亮,2006.水声定位技术在海洋工程中的应用研究初探.中国海洋大学.
何高文,刘方兰,2000.多波束测深系统声速校正.海洋地质与第四纪地质,20(4):109-114.
兰华林,2007.深海水声应答器定位导航技术研究.哈尔滨工程大学.
李胜全,2001.声速剖面测量.海洋测绘,4:28.
刘伯胜,雷家煜,1997.水声学原理.哈尔滨:哈尔滨工程大学出版社.
陆秀平,边少锋,黄谟涛,等,2012.常梯度声线跟踪中平均声速的改进算法.武汉大学学报信息科学版,37(5):590-593.
齐娜,田坦,2003.多波束条带测深中的声线跟踪技术.哈尔滨工程大学学报,24(3):245-248.
孙革,2007.多波束测深系统声速校正方法研究及其应用.中国海洋
大学.
王燕,梁国龙,2002.一种适用于长基线水声定位系统的声线修正方法.哈尔滨工程大学学报,23(5):32-34.
王燕,林旺生,梁国龙,2009.声线弯曲对同步水声定位系统影响分析及修正.声学技术,28(5):123-124.
张红梅,2010.水下导航定位技术.武汉:武汉大学出版社.
张居成,郑翠娥,孙大军,2013.用于声线跟踪定位的自适应分层方法.哈尔滨工程大学学报,34(12):1-6.
赵建虎,2002.多波束测深及图像数据处理方法研究.武汉大学.
赵建虎,刘经南,2008.多波束测深及图像数据处理.武汉:武汉大学出版社.
朱小辰,刘雁春,肖付民,等,2011.海道测量多波束声速改正精确模型研究.海洋测绘,31(001):1-3.

