在双Lamder模型中实现可调控光子带隙

巴 诺, 王 磊, 吴向尧， 李东飞， 王 丹, 严立云

(1.吉林师范大学物理学院， 四平 136000; 2.吉林大学物理学院, 长春 130012)

在双Lamder模型中实现可调控光子带隙

巴 诺1, 王 磊2, 吴向尧1， 李东飞1， 王 丹1, 严立云1

(1.吉林师范大学物理学院， 四平 136000; 2.吉林大学物理学院, 长春 130012)

研究驻波场相干驱动下四能级双Lamder模型的电磁感应光子带隙.当耦合场是远共振或共振时，来自于两邻近能级间的自发辐射相干效应(SGC)有助于实现一个或两个光子带隙.当自发辐射相干效应不存在时，探测场被原子系统强烈吸收，因此导致光子带隙严重形变甚至无法形成.数值结果表明，光子带隙结构是由SGC效应导致探测场和耦合场之间的相干增强Kerr非线性调制而产生，并改变驻波场的耦合方式，使系统实现单光子带隙转变为双光子带隙的动态调控.

量子光学； 电磁感应透明； Kerr非线性； 光子带隙

1 引 言

在人造复杂的材料中有效控制光子的流动性已经成为当今量子信息领域的热门话题，因为它可以用于实现更精细和更快速的光子电路和光子设备.光子晶体，作为杰出的人造材料之一，于上世纪八十年代由Jhon和Yablonovitch分别提出[1,2].光子晶体又叫光子带隙，是由介电常数不同的材料周期性排列形成的结构，当某些频率的电磁波与它作用时，由于满足Bragg反射条件不能传播而被完全反射回来，因此形成带隙结构.对于传统方法制备的光子晶体，其带隙的位置和宽度将固定不变，不利于灵活控制光子的流动性.于是，人们提出利用电磁感应透明技术(EIT)实现动态可调的光子带隙结构[3-5].电磁感应透明技术[6-9]是光和物质相互作用的一个有效途径，它可以控制物质的吸收、色散和非线性效应以及光的传播行为.一般情况下，行波场驱动的原子系统可以用来获得慢光[10]，光存储[11]，增强光的非线性[12]等.然而，利用驻波场驱动原子系统时，探测场的折射率在空间上被周期调制，形成一维具有周期性结构的光子带隙结构[13,14].这种电磁感应的光子带隙用于产生静止光脉冲[15,16]，实现光路由[17,18]等.

众所周知，一般介质的光学非线性非常弱并伴随着强的线性和非线性吸收，为了克服这个缺点，人们利用原子相干效应提高Kerr非线性同时抑制各种吸收.近年来，增强光学非线性已经用于实现量子相位门[19,20]、光开关[20,21]和光孤子的产生[23,24]等.在这些有趣的现象中原子相干效应的产生至少需要耦合场的相干作用.然而，原子相干效应也可以产生于自发辐射过程，所谓自发辐射相干是原子从靠得足够近的上能级向同一下能级衰减产生的干涉效应.自发辐射相干(SGC)可导致许多现象，如无反转光放大[25]，自发辐射变窄和淬灭[26]，诱导透明衰减[27]，和增强的克尔非线性[28].基于自发辐射相干(SGC)，研究者提出在一个四级双Lamder原子系统中增强Kerr非线性用于实现高效率衍射相位光栅[29].在本论文中，研究驻波场驱动下双Lamder原子系统的光学响应，讨论SGC效应能够增强Kerr非线性并抑制线性吸收从而有利于光子带隙结构形成.理论计算指出，通过控制驻波场的耦合方式可以使系统实现从单光子带隙到双光子带隙的动态调控.

2 理论模型

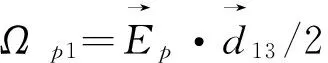
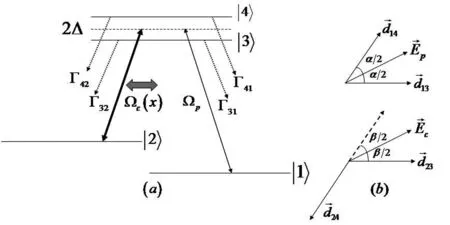
图1 具有SGC效应四能级双Lamder型原子系统Fig. 1 A four-level double Lamder atomic system with SGC

在电偶极矩和旋转波近似下，利用自发辐射Weisskopf-Wigner理论，通过求解稳态条件下几率幅的运动方程我们可以得到探测场极化率，其表达式是：

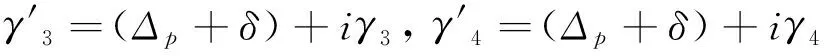
式中χ(1)和χ(3)对应于探测场极化率的一阶线性部分和三阶交叉Kerr非线性部分，分别为：

当耦合场是驻波形式时，我们进一步给出其平方拉比频率，

其中Ωc0表示耦合场的拉比频率幅值，Λ=λc/[2cos(θ/2)]是沿x轴方向的空间周期性，它可以通过改变驻波场的前向场和后向场之间的入射角θ来调节.

式中E+和E-分别表示向前和向后的探测场电场.κ=κ′+κ″是复的Bloch波矢，表示光子的带隙结构，可以通过求解方程e2iκa-Tr[M(Δp)]eiκa+1=0和detM=1得到.

布洛赫波矢用于描述探测场在一个无限周期内的光子带隙结构.对于一个长度l=Na的介质，N是驻波的周期数，探测场在其的反射谱系数和透射谱系数分别是:

其中MN(ij)是MN=MN中的矩阵元素.因此，探测场经过整个样品之后的反射率、透射率分别为R(Δp)=|rN|2，T(Δp)=|tN|2.

3 数值结果和分析

由于耦合场的强度依赖于驻波场的形式，所以导致探测场的折射率经历了周期性的调制.因此，具有恰当频率的探测场入射到周期性结构上，满足Bragg条件而被反射回来.在这一部分中，我们给出电磁感应光子带隙的反射谱和透射谱的数值结果.

[29]，pq<0能够增强Kerr非线性同时抑制吸收，因此取p=1，q=-1 .而且，高能级向低能级自发辐射弛豫速率分别为Γ31=Γ32=2.0γ，Γ41=Γ42=2.0γ，所有的参数是以γ=1.0MHz为数量级.

3.1SGC的非线性调制下形成单光子带隙

图2 当驻波场远离共振时探测场折射率的虚部随失谐的变化曲线Fig. 2 The imaginary part of the refractivity versus the probe detuning when the standing wave field is far away from resonance

在图3中，我们给出探测场的吸收部分Im(n)和折射部分Re(n)随驻波场传播方向的变化情况，黑实线和红虚线对应SGC效应存在，蓝点线是没有SGC效应.图中结果表明，SGC效应不仅能增强折射率调制深度，也能强烈抑制吸收，这与图2结论一致.产生上述现象的原因是，探测场和耦合场之间的Kerr非线性增强折射率周期性调制[见图3(b)中的红色虚线].这个周期性调制能使频率满足Bragg条件的探测场形成光子带隙结构，由此图4分别给出光子晶体的布洛赫波矢以及探测场的反射谱和透射谱.从图4(a)和4(b)可以看出，在SGC效应出现时，一个完美的光子带隙结构出现在κ′=π/a且κ″≠0的频率范围，并且图中的黑实线和红虚线几乎完全重合，这表明所有阶极化率对布洛赫波矢的影响和三阶非线性效应对布洛赫波矢的影响是一样的.然而，由于高阶吸收的影响使得所有阶的反射率和透射率(黑色实线)稍低于三阶非线性Kerr效应情况下的结果(红色虚线)[如图4(c)和4(d)].而在没有SGC的情况下，探测场被介质吸收，因此，反射率和透过率都为零[如图4(c)和4(d)中的蓝色点线]，不能形成光子带隙结构.

图3 给出在驻波场远离共振时折射率的虚部(a)和实部 (b)沿驻波场方向周期性演变图Fig. 3 When the standing wave field is far away from resonance, the real part (a) and imaginary part (b) of refractivity in the direction of the standing-wave field, respectively

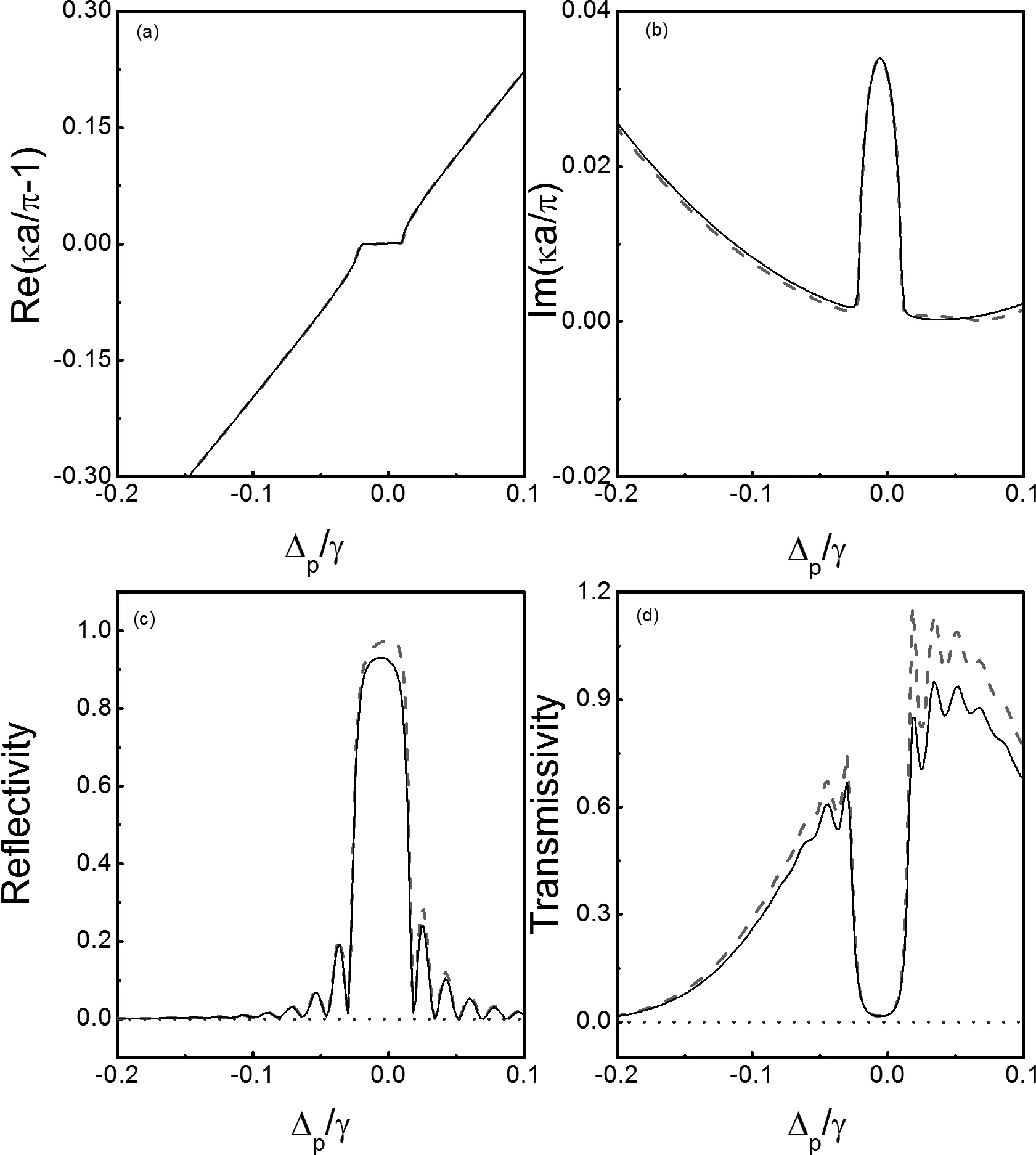
图4 是当驻波场远离共振时在第一布里渊区附近产生的PBG，(a)Bloch波矢的实部；(b)Bloch波矢的虚部；(c)探测场的反射谱；(d)探测场的透射谱Fig. 4 When the standing wave field is far away from resonance, photonic band gap structure near the first Brillouin zone boundary, (a) the real part of Bloch wave vetor; (b) the imaginary part of Bloch wave vetor; (c) the probe reflectivity; (d) the probe transmissivity

3.2SGC的非线性调制下形成双光子带隙

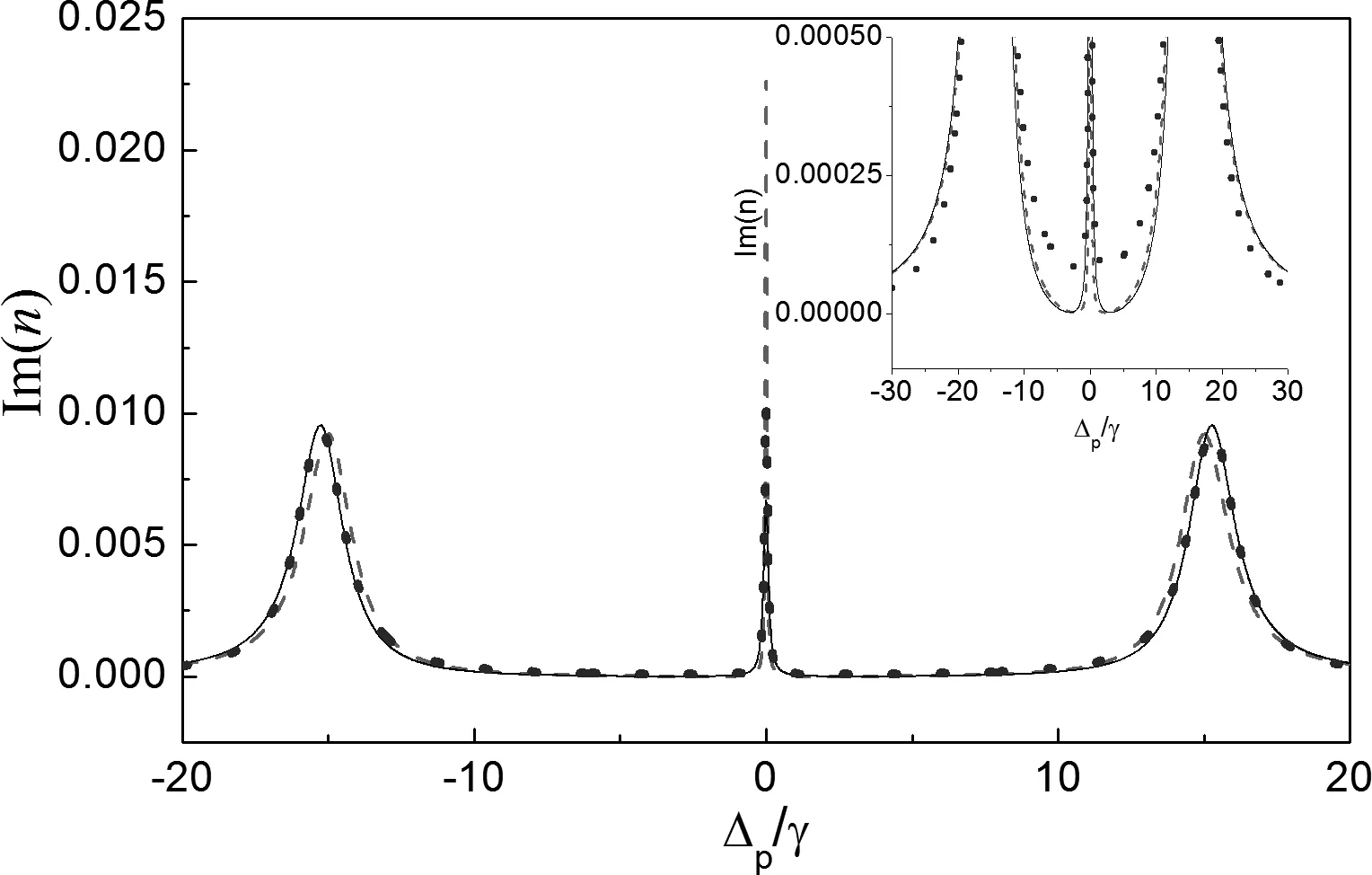
图5 当驻波场共振时探测场折射率的虚部随失谐的变化曲线Fig. 5 The imaginary part of the refractivity versus the probe detuning when the standing wave field is resonance

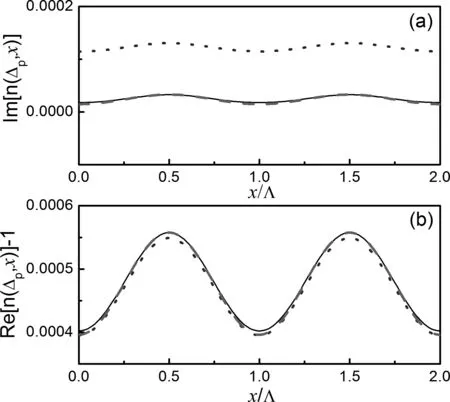
图6 在驻波场共振时分别给出折射率的虚部(a)和实部(b)沿驻波场方向周期性演变图Fig. 6 When the standing wave field is resonance, the real part (a) and imaginary part (b) of refractivity in the direction of the standing-wave field, respectively

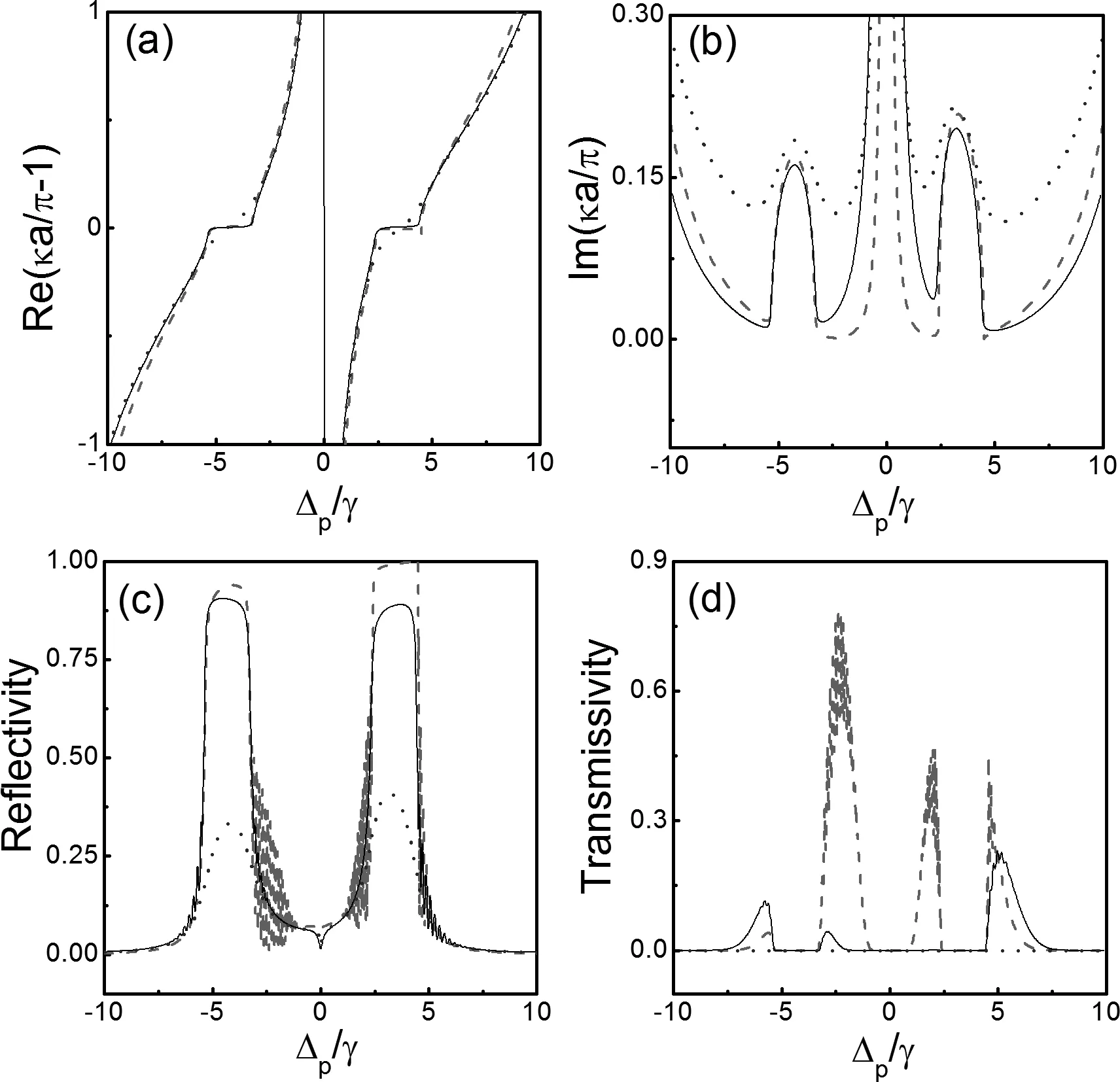
图7 是当驻波场共振时在第一布里渊区附近产生的PBG，(a)Bloch波矢的实部；(b)Bloch波矢的虚部；(c)探测场的反射谱；(d)探测场的透射谱Fig. 7 When the standing wave field is resonance, photonic band gap structure near the first Brillouin zone boundary, (a) the real part of Bloch wave vetor; (b) the imaginary part of Bloch wave vetor; (c) the probe reflectivity; (d) the probe transmissivity

4 结 论

总之，我们研究了具有SGC效应的双Lambda原子系统在驻波场作用下的稳态光学响应.由于驻波场强度的周期性变化导致探测场的折射率也被周期性调制，于是原子系统呈现出一维光子带隙结构.当驻波场非共振时，由SGC效应增强非线性相位调制产生一个透明窗口，于是对应形成一个具有高反射率的单光子带隙结构.而没有SGC效应的情况下，介质对探测场具有强烈吸收导致系统无法形成带隙结构.当驻波场共振时，由于空间被双暗态调制产生两个透明窗口，于是对应形成双光子带隙结构.然而，随着SGC效应消失探测场被吸收，导致光子带隙结构严重形变.这种动态调控光子带隙结构可以用来设计新型的光学器件，如全光路由和全光开关，它在光学网络和信息处理具有重要的应用价值.

参考文献：

[1]YablonovitchE.Inhibitedspontaneousemissioninsolid-statephysicsandelectronics[J].Phys.Rev.Lett., 1987, 58(20): 2059.

[2] John S.Strong localization photonsin certain disordered dielectricsuper-lattices[J].Phys.Rev.Lett., 1987, 58(23): 2486.

[3] Artoni M, La Rocca G C.Optically tunable photonic stop bands in homogeneous absorbing media[J].Phys.Rev.Lett., 2006, 96: 073905.

[4] Wu J H, La Rocca G C, Artoni M.Controlled light-pulse propagation in driven color centers in diamond[J].Phys.Rev. B, 2008, 77: 113106.

[5] Ba N, Wu X Y, Liu X J,etal. Tunable triple photonic band-gaps based on coherent induction in a five-leved 87Rbatomic system[J].ActaOpticaSinica, 2012, 31(11): 0827001 (in Chinese)[巴诺, 吴向尧, 刘晓静, 等.五能级87Rb原子系统中相干诱导的可调谐三光子带隙[J].光学学报， 2012, 31(11)： 0827001]

[6]HarrisSE.Electromagneticallyinducedtransparency[J].Phys.Today, 1997, 50(7): 36.

[7] Fleischhauer M,etal. Electromagnetically induced transparency: Optics in coherent media[J].Rev.Mod.Phys., 2005, 77: 633.

[8] Hu X H, Hou B P.Multiple electromagnetically induced transparency in a five-level atomic system [J].J.At.Mol.Phys., 2008, 25(2): 375 (in Chinese)[胡小会， 候邦品. 五能级原子系统中多重电磁诱导透明[J]. 原子与分子物理学报， 2008, 25(2)： 375]

[9] Zeng Z Q, Wang Y P.Absorption and dispersion of a V-type three-level atom driven by a microwave field[J].J.At.Mol.Phys., 2013, 30(6): 965 (in Chinese)[曾志强， 王玉强.微波场驱动下V型三能级原子的吸收和色散特性[J].原子与分子物理学报， 2013, 30(6)： 965]

[10] Hau L V, Harris S E, Dutton Z,etal.Light speed reduction to 17 metres per second in an ultracold atomic gas[J].Nature, 1999, 397: 594.

[11] Fleischhauer M, Lukin M D. Dark-state polaritons in electromagnetically induced transparency [J].Phys.Rev.Lett., 2000, 22: 5094.

[12] Harris S E, Field J E, Imamolu A. Nonlinear optical processes using electromagnetically induced transparency [J].Phys.Rev.Lett., 1990, 64: 1107.

[13] Artoni M, La Rocca G C. Optically tunable photonic stop bands in homogeneous absorbing media [J].Phys.Rev.Lett., 2006, 96: 073905.

[14] Wu J H, La Rocca G C, Artoni M. Controlled light-pulse propagation in driven color centers in diamond [J].Phys.Rev. B, 2008, 77: 113106.

[15] Bajcsy M, Zibrov A S, Lukin M D. Stationary pulses of light in an atomic medium [J].Nature, 2003, 426: 638.

[16] Zhang Y, Zhang Y, Zhang X H,etal. Efficient generation and control of robust stationary light signals in a double-Λ system of cold atoms [J].Phys.Lett. A, 2012, 656: 376.

[17] Gao J W, Wu J H, Ba N,etal. Efficient all-optical routing using dynamically inducedtransparency windows and photonic band gaps [J].Phys.Rev. A, 2010, 81: 013804.

[18] Wan R G, Kou J, Jiang L,etal. Magneto-optical switching and routing via coherently induced photonic band gaps in a driven Fe = 0 ↔ Fg = 1 transition [J].J.Phys. B, 2011, 44: 065502.

[19] Ottaviani C, Vitali D, Artoni M,etal. Polarization qubit phase gate in driven atomic media [J].Phys.Rev.Lett., 2003, 90: 197902.

[20] Ba N, Wan R G, Jiang B N,etal. Polarization phase gate and three-photon GHZ state using coherently enhanced Kerr nonlinearity [J].Opt.Commun., 2010, 283: 1017.

[21] Harris S E, Yamamoto Y. Photon switching by quantum interference [J].Phys.Rev.Lett., 1998, 81: 3611.

[22] Yan M, Rickey E G, Zhu Y F. Observation of absorptive photon switching by quantum interference [J].Phys.Rev. A, 2001, 64: 041801(R).

[23] Wu Y, Deng L. Ultraslow optical solitons in a cold four-state medium [J].Phys.Rev.Lett., 2004, 93: 143904.

[24] Huang G X, Hang C, Deng L. Gain-assisted superluminal optical solitons at very low light intensity [J].Phys.Rev. A, 2008, 77: 011803.

[25] Harris S E. Lasers without inversion: Interference of lifetime-broadened resonances [J].Phys.Rev.Lett., 1989, 62: 1033.

[26] Zhu S Y, Scully M O. Spectral line elimination and spontaneous emission cancellation via quantum interference [J].Phys.Rev.Lett., 1996, 76: 388.

[27] Paspalakis E, Kylstra N J, Knight P L. Transparency induced via decay interference [J].Phys.Rev.Lett., 1999, 82: 2079.

[28] Niu Y P, Gong S Q. Enhancing Kerr nonlinearity via spontaneously generated coherence [J].Phys.Rev. A, 2006, 73: 053811.

[29] Ba N, Wang L, Wu X Y,etal.Electromagnetically induced grating based on the giant Kerr nonlinearity controlled by sponteously generated coherence[J].Appl.Opt., 2013, 52: 4264.

Tunable photonic bandgap in double Lamder configuration

BA Nuo1, WANG Lei2, WU Xiang-Yao3, LI Dong-Fei3, WANG Dan3, YAN Li-Yun1

(1.Institute of Physics, Jilin Normal University, Siping 136000, China; 2.College of Physics, Jilin University, Changchun 130012, China)

We investigate a four level double lamder system with spontaneously generated coherence (SGC) for achieving photonic band gaps (PBG) by a standing-wave field. When the coupling field is far away from resonance or resonant, we can obtain one-phonon bandgap or two-phonon bandgap due to spontaneous emission coherent from two decay pathways. When the SGC is absent, the probe field is absorbed by the medium, so the PBG cannot be generated. The numerical calculations show that the induced PBG result from the Kerr nonlinear modulation between the probe and coupling field, and by controlling the detunings of coupling field, one PBG can be dynamically tuned into two PBGs in this system.

Quantum optics; Electromagnetically induced transparency; Kerr nonlinear; Photonic bandgap

103969/j.issn.1000-0364.2015.12.019

2015-04-28

国家自然科学基金(1347137，11247201，11374126)；吉林省教育厅"十二五"科学研究项目(吉教科合字[2015]第215号)；吉林师范大学博士项目(2011022)

巴诺(1980—),女,讲师，博士，研究方向为量子光学.E-mail: banuo2008@163.com

O431.2

A

1000-0364(2015)06-1027-06