附加黏滞阻尼器平面不对称结构基于性能的减震控制研究

余能彬 付君宜，* 赵园园 吴 斌

(1．贵州正业工程技术投资有限公司，贵州省岩溶地基工程技术研究中心，贵阳550000;2．长安大学建筑工程学院，西安710061)

1 引言

当遭遇地震后，尤其在罕遇地震后，虽然结构通常可以保证不倒塌，但是由于维修难度太大或者造价高昂，这些建筑通常无法使用。当前规范的抗震设防目标仅保证人身安全，已经无法达到人们的需求，基于性能的抗震设计理论的提出能够有效地解决这一问题，该理论由美国科学家首次提出［1］。在美国，FEMA273/274给出了建立在结构反应与等效单自由度体系基础上的静力分析方法，目前这一设计理论已被不少国家规范采用［2－3］。

消能减震结构是一种新型的抗震结构，通过将结构中的一些非承重构件设计为耗能构件，或是在结构的特定部位加设消能装置，大量消耗地震引起的结构能量，快速降低结构的振动反应［4］。本文通过非线性静力分析方法“能力谱”法，以质心、刚心不重合的框架结构为模型，结合我国规范规定地震作用下的变形限值，提出附加粘滞阻尼结构基于性能的抗震设计方法。

2 能力谱法的原理和步骤

Freeman等［5］学者首先提出能力谱法的设计原理，并由Faifar等学者补充修改。能力谱法的实质是一种非线性静力分析方法，它由两部分构成:建立能力曲线和需求曲线，通过阻尼比折减规律找出满足性能目标时的附加阻尼比;通过能力曲线和需求曲线对已有结构进行性能评价。具体过程如下所示:

(1)通过规范对结构进行初步设计。

(2)通过一定形式的侧向力分布形式对结构进行推覆分析。

(3)由推覆曲线通过式(1)转化成能力曲线:

式中，Sa为谱加速度;Sd为谱位移，γ1表示为结构第一振型模态质量和参与系数;un表示结构顶点位移;Vb表示基底剪力。

(4)通过规范和阻尼比折减规律，建立一系列不同阻尼比下的需求曲线，将需求曲线和能力曲线在同一坐标系中画出，找出满足目标位移时所对应的需求曲线，该需求曲线所对应的阻尼比即为结构所需的总阻尼比。

(5)由附加阻尼比计算出阻尼系数，并进行分配。

该方法认为结构变形以第一振型为主，未考虑扭转振型的影响和其他振型的影响，对于平动扭转耦合严重的结构计算精度较低，针对平动扭转耦合严重的平面不对称结构的设计方法仍需进一步研究。

3 能力谱曲线和需求谱曲线的建立

3．1 能力谱曲线的建立

推覆分析作为静力非线性分析方法的一种，其侧向力分布模式有多种，本算例使用第一阶振型模态力为侧向力分布，对结构进行加载，加载到结构倒塌为止，该过程可以得到基底剪力与顶点位移关系曲线［6］。

将推覆曲线转化成能力曲线，即Sa－Sd谱加速度与谱位移曲线。其中，Sa谱加速度和Sd谱位移由式(1)求得。W1和γ1分别按下式计算:

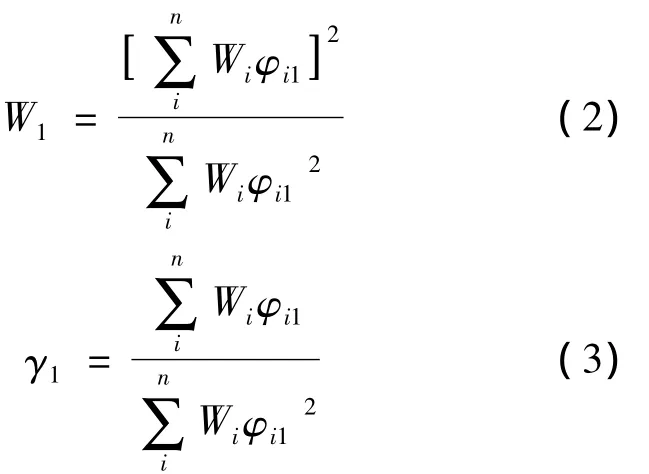
式中，Wi为第i层楼层质点的重量;φi1为第一振型向量的值，顶层值通常正交化为1;W1为第一振型模态重量;γ1为第一振型参与系数。

3．2 需求谱曲线的建立

需求谱的建立是利用我国规范的加速度反应谱，通过下式转换为Sa－Sd谱曲线。

由我国规范的加速度反应谱可得Sa的计算方法如式(5)所示。当T≤0．1时，

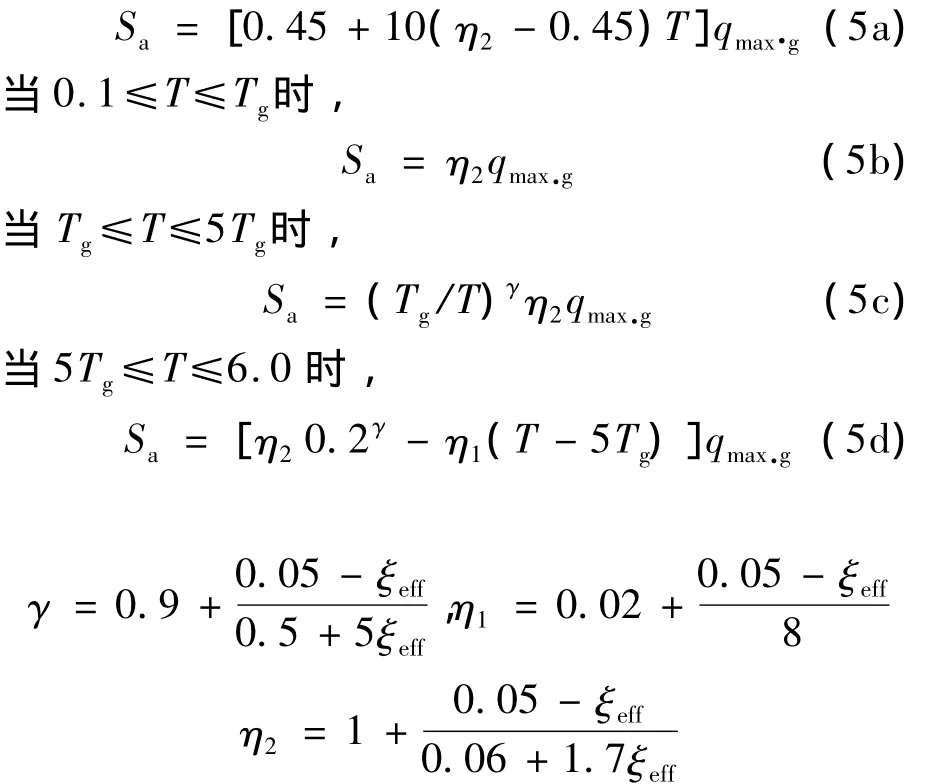
式中，qmax表示水平地震影响系数最大值;Tg表示场地特征周期;ξeff表示附加阻尼器结构的等效阻尼比［7］。

4 阻尼器设计

附加阻尼器的结构，其总阻尼比包括以下三部分:弹性状态下结构的阻尼比ξ0;弹塑性状态下结构的滞回耗能所对应的等效阻尼比ξμ;附加阻尼器为结构提供的附加等效阻尼比ξsd。

式中，ξ0为结构弹性状态下的阻尼比，通常混凝土结构取0．05，钢结构取0．02;ξv表示结构进入弹塑性状态后，附加阻尼器对应弹性周期以简谐运动的方式所提供的阻尼比;α表示结构能力曲线第二刚度系数;ξu表示弹塑性状态下结构滞回耗能对应的等效黏滞阻尼比，本文采用的滞回模型为 Gukan 和 Sozen 模型［8］，ξu计算方法如式(8)所示，μ为结构延性系数，r表示结构屈服后和屈服前刚度比:

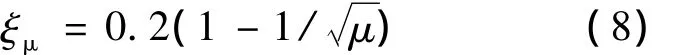
由式(6)得出阻尼器所需提供的附加阻尼比:

通过阻尼器附加阻尼比ξsd可以计算出结构各层对应的阻尼系数，本文阻尼器布置方法采用均匀布置方式，每层阻尼系数均相同。假设结构中所有阻尼器的非线性指数相同，x和y方向的阻尼系数与阻尼比之间的关系见式(10)［9］:

式中，D表示结构顶点位移(目标位移);N表示结 构 层 数值可在FEMA273［10］中查找，φxi1为 x方向第一振型向量的值

平面不对称结构的x和y方向都需要布置阻尼装置，x，y向阻尼系数按照第一振型顶层x，y向最大位移比进行分配，见式(11):

式中，Dx和Dy分别为结构x，y向第一振型顶层最大位移;Cx和Cy分别为每层x向与y向的总阻尼系数。

联立式(10)和式(11)可得出楼层每层的两个方向的总阻尼系数，Cx总和Cy总。

由于结构在y向不对称，对结构质量系数超过90%的振型，其y向两端位移分别进行SRSS组合，组合结果分别为Dy组左和Dy组右，按照组合后的两端位移比进行阻尼系数分配，联立式(12)和式(13)，得出 Cy左和 Cy右。

式中，Di左和Di右表示结构左右两端第i阶模态的顶点位移。

5 算例分析

随着消能减震技术的发展成熟，结构可以通过消能装置来达到抗震的目的，同时可以通过性能目标来控制结构在不同等级地震做用下所处的不同状态。本文以12层钢筋混凝土结构为例，基于性能目标来附加非线性粘滞阻尼器，以达到理想的抗震效果。

5．1 结构初步设计和性能目标

本算例为一幢12层混凝土框架，一层层高为3．6 m，其余各层层高均为3．3 m。建筑标准层平面图如图1所示。1－6层柱子截面尺寸为600 mm×600 mm，7－12层柱子截面500 mm×500 mm，结构中，y方向中梁截面尺寸为400 mm×200 mm，其余梁截面尺寸均为500 mm×200 mm。梁、柱均采用C30混凝土，受力钢筋为HRB335级钢筋。抗震设防烈度为八度，建筑场地类别为II类，抗震等级为二级，场地特征周期(Tg)为0．40 s，设计基本地震加速度值为 0．20 g。结构最左侧框架柱子附加节点质量，附加质量大小如图1所示，结构刚度均匀，刚心即为结构几何型心，质心沿x向偏心，沿y向对称，属于单向偏心结构。附加阻尼器结构的性能目标是保证中震作用下使用无害，层间位移角限值为1/550。本算例以最左侧一榀框架的顶点为控制点，该榀框架y向第一阶振型向量为(1，0．97，0．93，0．87，0．79，0．71，0．6，0．49，0．38，0．27，0．15，0．05)，假定结构按照第一振型形状变形，则由最大层间位移角限值得到结构的顶点位移δ=50 mm。

图1 结构标准层平面图(单位:mm)Fig．1 Layout plan of standard floor of structure(Unit:mm)

罕遇地震作用下结构的性能目标满足可修，层间位移角限值为1/150，同上得到罕遇地震作用下的顶点位移δ=185 mm。

5．2 结构动力特性

图2 Sap2000模型Fig．2 Model of Sap2000

结构动力特性如表1所示，该结构第一阶振型以y方向平动为主并伴随扭转，第二振型为x方向平动，第三阶振型为扭转伴随y向平动。

表1 结构动力特性Table 1 Structural dynamic characteristics

5．3 附加阻尼比计算和阻尼器设计

应用Sap2000中的需求谱(见图2)，通过阻尼比折减规律得到满足罕遇地震下结构目标位移时的阻尼比，由式(3)计算得到γ1=1．30。使所建需求曲线与能力曲线的交点所对应的谱位移接近目标顶点位移，转换的谱位移185/1．3=142 mm，如图3所示。

图3 罕遇地震作用下能力曲线和需求曲线Fig．3 Capacity curve and the demand curve under rare earthquake

需求谱对应的总阻尼比ξ=0．27。则结构的滞回耗能对应的等效粘滞阻尼比由式(8)得ξμ=0．056，因此满足目标位移时的阻尼器所提供的附加阻尼比为 ξsd=ξ－ξ0－ξμ=0．164。由于结构已经进入弹塑性状态，结构能力曲线第二刚度系数α =0．078，ξμ=0．056，由式(7)可得 ξv=0．122。5．3．1 非线性黏滞阻尼器设计

结构每层阻尼器布置均相同，分布方式如图4所示，阻尼器与楼层夹角均为 32．4°，由 ξv=0．122，联立式(10)和式(11)得到每层 y向阻尼系数 Cy总=168 401 N · s/mm;Cx总=6 120 N·s/mm。如图4所示，由于结构在x方向对称，阻尼器布置方式为沿四周均匀布置，则每个阻尼器的阻尼系数为Cx总/4=1 052 N·s/mm;y向阻尼系数的分配方式见式(12)和式(13)，计算结果Cy左=89 542．96 N · s/mm，Cy右=78 858．04 N·s/mm，由于结构左侧位移较大，在y方向每层布置6个阻尼器，最左侧两品框架共布置4个阻尼器，阻尼系数为Cy左/4=22 kN·s/mm，最右侧框架布置2个阻尼器Cy右/2=39 kN·s/mm;所有阻尼器的非线性系数均为α=0．5。

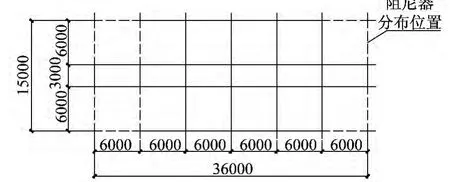
图4 阻尼器分布(单位:mm)Fig．4 The damper distribution(Unit:mm)

5．3．2 时程分析

本文通过非线性时程分析以验证计算结果的有效性，选取地震波为一条与场地匹配的人工波和一条实测地震波LACC_NOR－Z，中震作用下将地震波加速度峰值调整为200 cm/s2，罕遇地震作用下将地震波加速度峰值调整为400 cm/s2。选取好地震波后分别对原结构和附加阻尼器的结构进行时程分析，所得各楼层最大位移如图7和图8所示，各楼层层间最大层间位移角如表2和表3及图5和图6所示。

楼层1 2 3 4 5 6 7 8 9 10 11 12人工波 1 1 1 1 1 1 1 1 1 1 1 1 236 LAC-Z 1 143 85 79 83 80 85 85 92 103 127 165 1 1 1 1 1 1 1 1 1 1 1 165 92 80 83 87 94 97 114 114 138 183 275

表2 罕遇地震作用下无控制结构各层最大层间位移角Table 2 Maximum inter-story drift of structure without cortrol under rare earthquake表3 罕遇地震作用下有控制结构各层最大层间位移角Table 3 Maximum inter-story drift of controled structure under rare earthquake

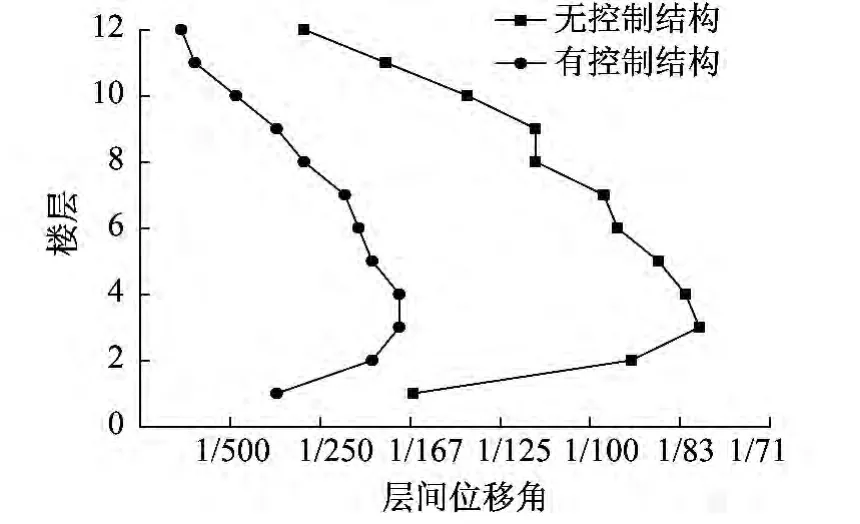
图5 最大层间位移角LAC-Z波Fig．5 The maximum inter-story drift of LAC-Z wave

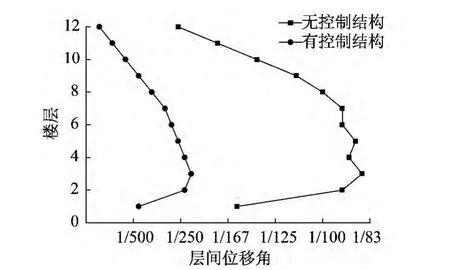
图6 最大层间位移角人工波Fig．6 The peak maximum inter-story drift of artificial wave

图7 最大楼层位移LAC-Z波Fig．7 The maximum displacement of the floors of LAC-Z wave

图8 最大楼层位移人工波Fig．8 The maximum displacement of the floors of artificial wave

中震作用下的各层最大层位移和层间位移角 结果如表4－表5及图9－图12所示。

表4 中震作用下无控制结构各层最大层间位移角Table 4 Maximum inter-story drift of stnutime wiehart control under moderate earthquake

表5 中震作用下有控制结构各层最大层间位移角Table 5 Maximum inter-story drift of controled structure under moderate earthquake

图9 人工波最大层间位移角Fig．9 The maximum inter-story drift of artificial wave

图10 LAC-Z波最大层间位移角Fig．10 The maximum inter-story drift of LAC-Z wave

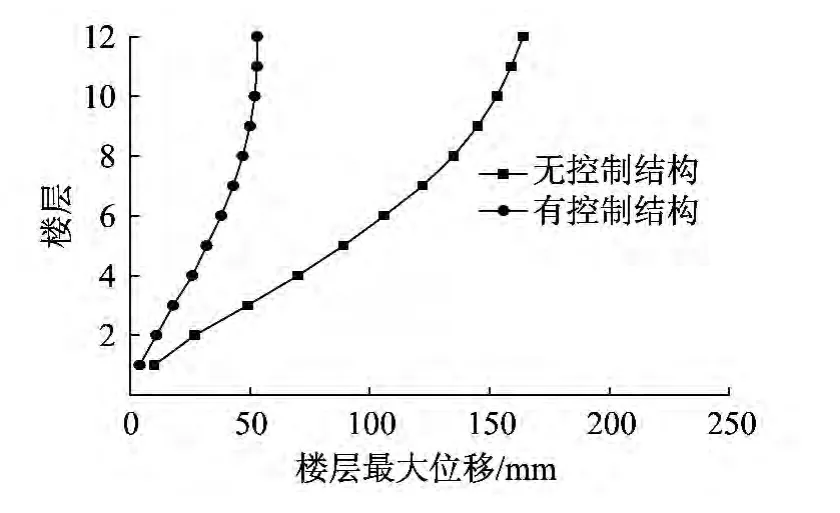
图11 LAC－Z波最大楼层位移Fig．11 The maximum displacement of the floors of LAC －Z

图12 LAC－Z波最大楼层位移Fig．12 The maximum displacement of the floors of artificial wave

由以上时程分析结果可以得出，附加阻尼器结构与原结构相比，其最大层位移和层间位移角都得到了很好的控制，且附加阻尼器结构在中震和罕遇地震下都能基本满足设定的目标位移和层间位移角限值要求。可以确定上述以能力谱法为基础的基于性能的抗震设计方法可以很好地满足性能目标的要求。

中震、罕遇地震下的最大层间位移角(第三层)时程图如图13—图16所示。

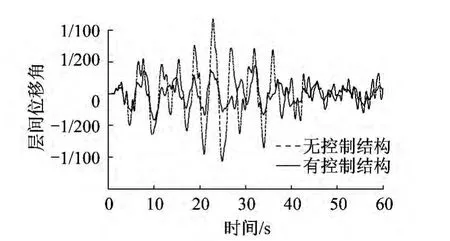
图13 人工波罕遇地震层间位移角Fig．13 Inter-story drift of floors of artificial wave under rare earthquake

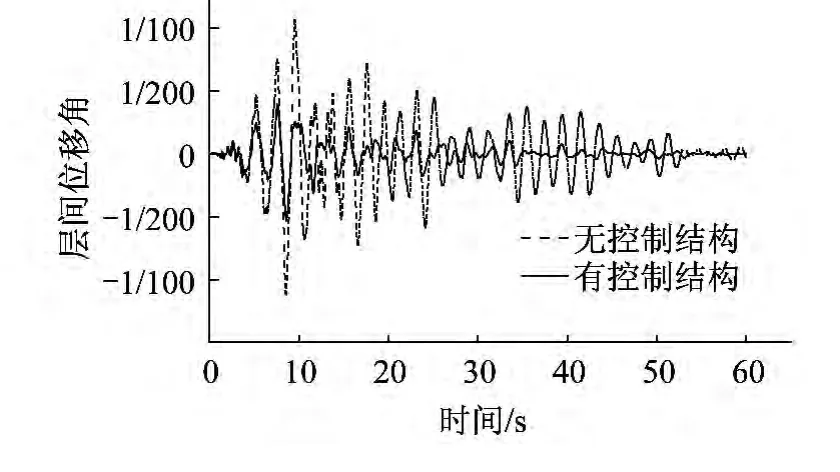
图14 LAC－Z波最大层间位移角Fig．14 The inter-story drift of LAC － Z wave under rave earthquake

图15 LAC－Z中震层间位移角Fig．15 The inter-story drift of LAC － Z wave under moderate earthquake

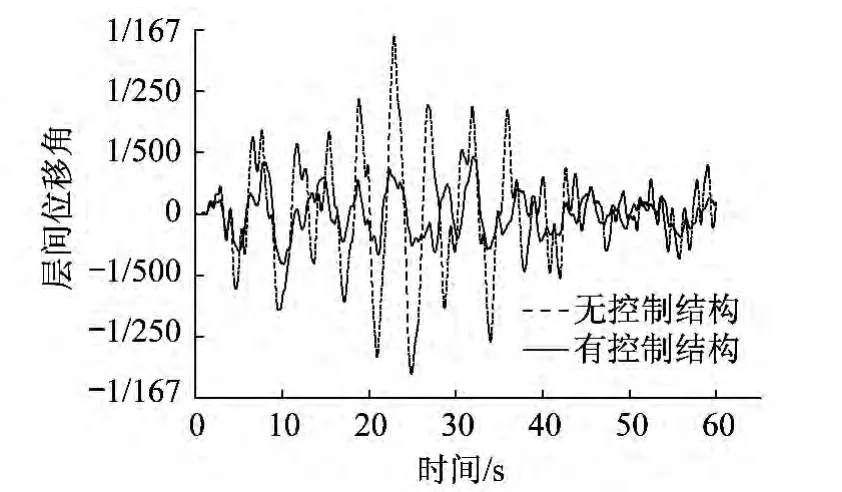
图16 人工波中震层间位移角Fig．16 The inter-story drift of artificial wave under moderate earthquake

由层间位移角时程分析图可以得出，基于能力谱法设计的附加黏滞阻尼器的消能体系无论是在中震作用下还是罕遇地震作用下，结构的层间位移角都得到了明显控制。

6 结论

(1)通过应用规范中的层间位移角限值，由结构第一阶振型的向量值，将层间位移角限值转化为结构顶点最大位移，得到结构顶点位移的性能目标。

(2)针对结构在地震作用下两个方向的位移不同，提出了一种平面不对称结构两个方向的阻尼系数分配的方式和单偏心结构在偏心方向的阻尼系数分配方式。

(3)本文针对结构基于性能的抗震设计方法，可以根据性能目标来确定附加阻尼比的大小，从而设计阻尼装置，与传统设计方法相比可以更为合理利用资源。

(4)本文将能力谱法应用于三维不对称结构，结果表明该方法对于平扭耦合不严重的平面不对称结构有较好的计算精度。

［1］ 李波，梁兴文，杨克家．非弹性单自由度体系附加粘滞阻尼器基于性能的抗震设计［J］．工程力学，2007，24(6):147－152．Li Bo，Liang Xingwen，Yang Kejia．Performance －based seismic design of supplemental viscous dampersfor inelastic SDOF systems［J］．Engineering Mechanics，2007，24(6):147 －152．

［2］ Kim J，Bang S．Optimum distribution of added viscoelastic dampers for mitigation of torsional responses of plan-wise asymmetric structures［J］．World Earthquake Engineering，2009，25(3):1257-1269．

［3］ Yoshida O，Dyke S J，Giacosa L M，et al．Experimental verification of torsional response control of asymmetric buildings using MR dampers［J］．Earthquake Engineeringand Structural Dynamics，2003，32(13):2085-2105．

［4］ 李冰，付君宜．平面不对称消能结构基于性能的抗震设计方法研究［J］．城市建设理论研究，2014，4(8):9-11．Li Bing，Fu Junyi．Performance-based seismic design of plan-asymmetric structures with energy dissipation Systems［J］．Urban Construction Theory Research，2014，4(8):9-11．(in Chinese)

［5］ 吉小萍，董军．Pushover能力谱方法的基本原理及应用［J］．四川建筑科学研究，2009，35(3):148-151．Ji Xiaoping，Dong Jun．Principle and application of pushover capacity spectrum［J］．Sichuan Building Science，2009，35(3):148-151．(in Chinese)

［6］ 陈志敏，高培，刘彩云，等．SAP2000中文版使用指南［M］．北京:人民交通出版社，2006．Chen Zhimin，Gao Pei，Liu Caiyun，te al．SAP2000 Chinese use guide［M］．Beijing:China Communication Press，2006．(in Chinese)

［7］ 李波，赵均海，梁兴文．附加黏滞阻尼器结构基于性能的抗震设计［J］．世界地震工程，2009，25(3):91-96．Li Bo，Zhao Junhai，Liang Xingwen．Performancebased seismic design of a structure with supplemental viscous dampers［J］．Engineering Structures，2009，25(3):91-96．(in Chinese)

［8］ Miranda E，Ruiz-Garaja J．Evaluation of approximate methods to estimate maximum inelastic displacement demands［J］．Earthquake Engineering and Structural Dynamics，2002，31(3):539-560．

［9］ Landi L，Diotallevi P P，Castellari G．A Procedure for the design of viscous dampers to be inserted in existing plan-asymmetric buildings［J］．Earthquake Engineering and Structural Dynamics，2009，28(5):633-653．

［10］ Federal Emergency Management Agency(FEMA)．Guidelines and commentary for the seismic rehabilitation of buildings［R］．The Building Seismic Safety Council，FEMA Report 273，1997．