基于向量式有限元的超高韧性水泥基复合材料叠合剪力墙非线性分析

刘 松 章红梅 师振华

(同济大学结构工程与防灾研究所，上海200092)

1 引言

普通混凝土材料，即普通混凝土材料具有良好的抗压强度，但其抗拉强度相对较弱，一旦混凝土受拉开裂，其内部钢筋易腐蚀，致使其钢筋混凝土构件性能下降甚至完全失效。为改善混凝土性能，超高韧性水泥基复合材料应运而生。超高韧性水泥基复合材料(UltraHighToughness Cementitious Composites)是当前发展起来的一种复合混凝土材料，其通过添加短纤维增强材料受拉特性，具有显著的应变硬化特征，开裂时裂缝多且细密，极限拉应变可稳定地达到3%以上［1－2］。超高韧性水泥基复合材料最早由密歇根大学的Victor Lee教授和麻省理工学院的Leung教授基于微观力学与断裂力学原理，提出材料的基本设计理念［3］。经过不断发展，超高韧性水泥基复合材料已经具有优良的抗拉性能、较高的应变硬化及多裂缝开裂能力。

剪力墙是一种抗震性能优良的结构构件，但普通混凝土由于受拉强度低，其边缘混凝土在结构遭受强风或地震作用下容易拉裂、压溃，使得剪力墙构件也往往因为边缘混凝土的退出工作而导致整体构件的失效或难于修复。采用超高韧性混凝土材料替换剪力墙边缘普通混凝土材料［4］，充分利用超高韧性混凝土抗拉强度高、裂缝分散等特点，可望使剪力墙获得更高的抗震性能。

向量式力学是一门依托计算机技术而发展起来的计算科学的理论，它提供了一套关于结构分析简洁明晰的系统理论模式，适合于分析结构的大变形和强非线性行为［5］。本文将基于新型非线性分析有限元理论——向量式有限元，开发新型板单元进行超高韧性混凝土边缘构件剪力墙的强非线性模拟，从而了解超高韧性混凝土叠合剪力墙的非线性行为和抗震性能。

2 向量式有限元板单元相关概念

2．1 向量式有限元简介

向量式有限元也称有限质点法，将结构离散成有限个质点，利用牛顿第二定律建立控制方程，引入传统有限元中单元的概念，描述质点系的相互作用。向量式有限元有三个核心新概念，即点值描述、途径单元、虚拟的逆向运动［6－7］。

1)点值描述

在空间上，将结构看成质点系，质点之间采用单元连接，构件的连接可设置连接单元。单元没有质量，用来描述质点之间的相互作用力，质点受到它周围单元所施加内力，单元内力集成到节点上，即为节点内力，节点(质点)在内外力作用下的运动满足牛顿力学第二定律，即

式中，M为质量矩阵;Pext表示外力;Pint表示内力。

2)途径单元

将整个运动过程划分为一系列足够短的时间片段，称之为途径单元，在一个途径单元内，单元既有刚体运动，也有变形，且运动连续。通过控制途径单元的大小，可以控制变形为小变形，使得传统基于小变形假设的理论能够适用。运动的不连续仅发生在途径单元之间(即途径单元首末时刻)，而且结构组合和单元特性均可在途径单元首末时刻改变。

3)虚拟的逆向运动

采用虚拟的逆向运动，以消除单元刚体位移，获得单元的纯变形，用公式表示，即

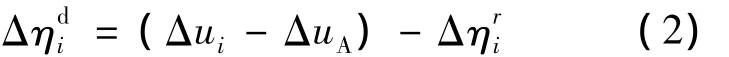
式中，Δui是节点在ta－tb时段内的位移;ΔuA是参考点在ta－tb内的位移。

向量式有限元对不同的结构形式，包括平面及三维的桁架、钢架、固体和板壳等，以及复杂的力学行为，包括大变形、空间运动、材料性质的变化、断裂和坍塌等，都可以用相同的概念和程序来处理。

2．2 向量式有限元二维板单元开发介绍

向量式有限元板单元的内力计算过程和传统有限元板单元有一些区别，其内力计算过程如下所示［8－10］:

第一步是计算一个途径单元内单元的纯变形，通过刚体逆向平动与转动，获取单元的近似纯变形，如图1所示，单元在 tn到tn+1时刻的纯变形为

其中，I是单位对角矩阵，转动矩阵R为

为了提高计算效率，向量式有限元引入新的坐标系——变形坐标，新的坐标系的选取有很多种方法，本文变形坐标系取单元节点1为坐标原点，并令X轴平行于节点2的位移向量。在变形坐标系中，单元节点坐标与节点位移为

图1 单元逆向转动［10］Fig．1 Virtual reverse rotation of element［10］

由有限元理论可知单元应变与节点位移间的关系:

其中，

最后，单元节点力采用虚功原理计算获得

图2 变形坐标［10］Fig．2 Deformation coordinate［10］

3 板单元程序计算流程图

二维板单元程序计算流程图如图3所示。

图3 计算流程图Fig．3 The calculation flow chart

程序包含两个主要部分:前处理和计算求解。前处理包括模型参数信息读入和必要的参数设置，求解部分包括求解和结果输出。必要的参数主要包括时间参数的设定和初始条件的设定。求解部分由两层循环构成，最外层是按时间步循环，第二层循环包含两类循环和一个输入:点值循环、单元循环和外荷载输入。点循环先调用内力子程序和外力子程序获得tn时刻内、外力信息，然后利用tn时刻节点位置信息计算tn+1时刻节点位置坐标。单元循环利用点循环计算出的tn和tn+1时刻节点位置坐标，通过虚拟的逆向运动计算单元纯变形，再利用有限元理论和虚功原理计算单元应力应变及单元节点内力，然后将单元节点内力集成到与其相连的质点上，并把结果返回给点循环，为点循环提供计算质点下一时刻位置的内力值。在单元循环中，每一次都要对单元做判断，如判断单元是否进入塑形，是否发生失效等，然后进行相关处理，在下一次进行单元循环时必须采用更新后的单元状态。判定单元性质变化是一个难点，此过程涉及单元失效准则的选取，以及失效后如何处理，因此需要后续的开发。外荷载的输入由外力子程序完成，可以输入随时间变化的外力值。

程序设计中有两点需要注意:一是局部坐标系的选择，局部坐标系既要能减少单元自由度，同时又要避免出现特殊状态致使计算不能进行，处理好局部坐标系的选择会大大增加计算的稳定性;另一个要注意的问题是本构关系的选取，因为内力是以增量的形式不断累积的，所以材料的弹性模量要取切线模量。

向量式有限元是基于动力学的思想来分析结构行为，计算静力及拟静力模型时，为缩短计算时间，可采用按比例增大质点质量的方法或者增大阻尼，此方法可极大地减少计算时间，同时不影响结果的准确性。在计算动力模型上，向量式有限元的分析过程更加符合真实结构的行为过程，同时避免了求解结构刚度矩阵。

4 超高韧性水泥基复合材料剪力墙非线性分析

为了解超高韧性钢筋混凝土剪力墙的抗震性能，本文选取同济大学国家重点实验室2006年进行的剪力墙变参数低周反复试验中两片典型剪力墙进行建模计算，并比较分析了边缘采用超高韧性混凝土材料和普通混凝土材料钢筋混凝土剪力墙的抗震性能差异。基于剪力墙低周反复试验的力－位移骨架曲线与其推覆的力－位移曲线基本一致［11］的研究结论，为简化计算，本测试中用推覆分析的方法对该试验模型进行对比分析。

4．1 钢筋混凝土剪力墙试验参数与UHTCC剪力墙设计参数

1)钢筋混凝土剪力墙试验参数

两片钢筋混凝土剪力墙尺寸相同，为1 000 mm×2 000 mm×125 mm，编号分别为SW6－3和SW1－1。剪力墙上下端设置有顶梁和底梁，顶梁用作加载梁，底梁用以固定试件。剪力墙内钢筋伸入顶梁和底梁内，且梁与墙整体浇筑，以保证剪力墙试件和顶梁底梁的有效连接。SW6－3剪力墙所用混凝土设计为C40，SW1－1剪力墙所用混凝土为C30。剪力墙配筋图如图4所示。

图4 剪力墙配筋详图(单位:mm)Fig．4 Reinforcement details of shear walls(Unit:mm)

表1列出了两片剪力墙详细试验参数。试验测得C30与C40混凝土100×100×300棱柱体抗压强度分别是 20．70 MPa 和 30．80 MPa［12－13］。

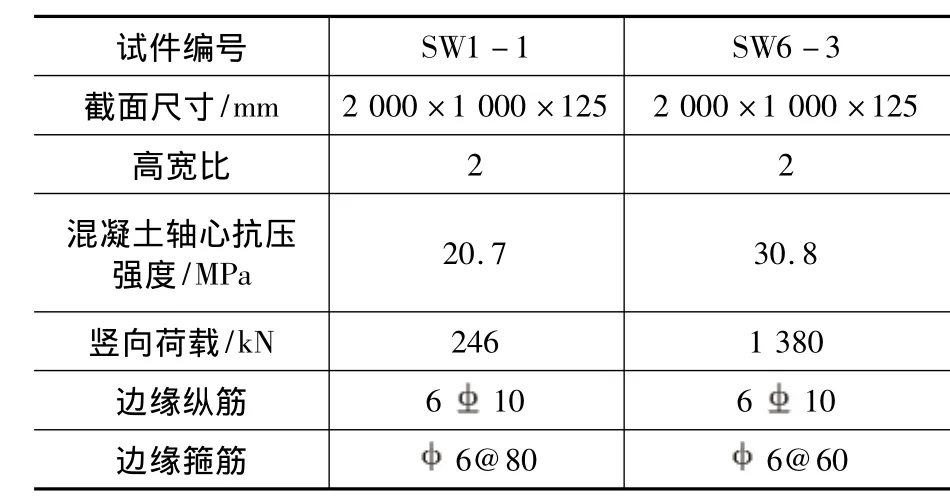
表1 试件试验参数Table 1 Experimental parameters of specimens

2)UHTCC剪力墙设计参数

本文中UHTCC剪力墙采用与普通钢筋混凝土剪力墙完全尺寸大小及配筋完全一致的设计方案，配筋详图可参看图5。UHTCC剪力墙只将原剪力墙箍筋约束区普通混凝土材料替换成超高韧性水泥基复合材料，其余均不改变，表2给出了UHTCC剪力墙试件的具体设计参数，其中混凝土轴心抗压强度是普通混凝土的取值，具体UHTCC强度的取值参考本构关系模型部分。

表2 UHTCC试件设计参数Table 2 Design parameters of UHTCC specimens

4．2 模型建立

4．2．1 剪力墙有限元模型

1)普通剪力墙有限元模型

普通剪力墙有限元模型示意图如图5所示，剪力墙有限元模型总共包含353个节点、306个四边形二维实体单元以及466个link单元。因剪力墙两侧边缘设置有箍筋，因此图中黑色加深部分采用约束混凝土模拟，其余部分为普通混凝土材料，边缘纵筋及箍筋按照实际情况采用杆单元建模，混凝土单元与钢筋单元之间采用共节点方式连接，未考虑钢筋与混凝土的粘结滑移。

图5 普通剪力墙模型示意图Fig．5 Sketch of RC wall model

2)UHTCC剪力墙有限元模型

如图6所示，UHTCC剪力墙除边缘箍筋约束区内采用UHTCC替代原普通混凝土材料外，其余模型信息与原普通剪力墙模型完全一致。

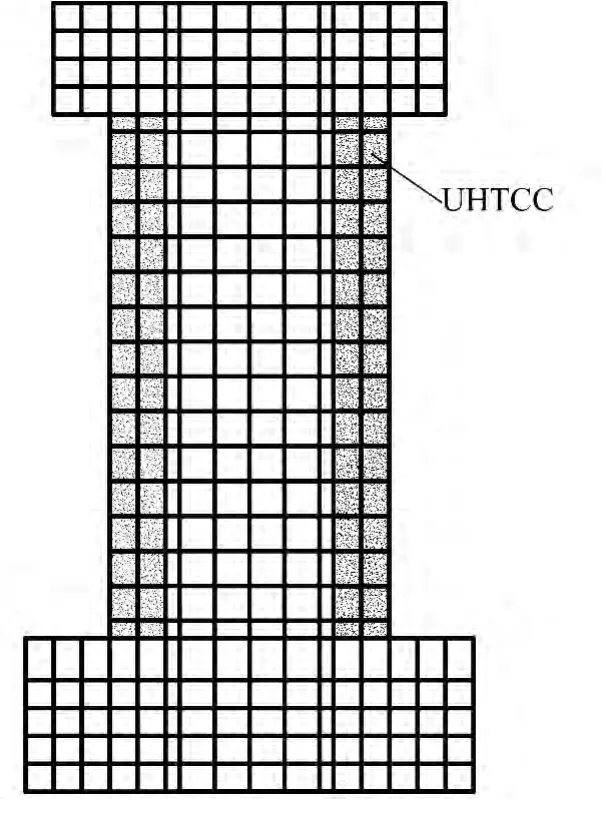
图6 UHTCC剪力墙模型示意图Fig．6 Sketch of UHTCC wall model

3)ABAQUS剪力墙有限元模型

ABAQUS中剪力墙有限元模型，采用实体单元C3D8R模拟混凝土及UHTCC，混凝土与UHTCC的本构关系都采用弹塑性损伤本构关系模型，本构关系曲线由试验值确定，受压、受拉应力峰值及对应应变均与VFIFE中取值相同。钢筋本构关系也采用与VFIFE中完全相同的双线性强化模型，模拟的边界条件及加载过程与VFIFE中均相同。ABAQUS的求解器采用standard隐式求解器，与VFIFE的显示求解是不同的。

4．2．2 本构模型

本文中VFIFE的模拟中普通混凝土本构关系模型采用Darwin-Pecknold模型，其等效单轴应力－应变关系曲线如图7所示。此处普通混凝土应力应变关系受压区采用Darwin建议曲线，上升段采用Saenz公式，下降段采用直线，残余应力取峰值应力的 0．2 倍［14－15］，在受拉区采用 Hillerborg建议的双折线模型［16］。

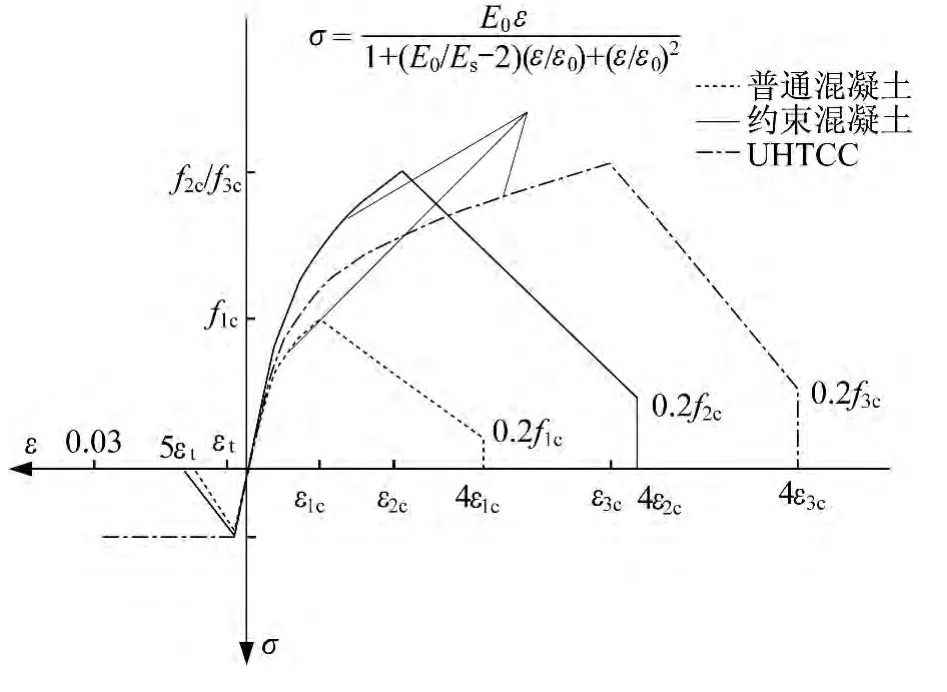
图7 混凝土本构关系模型Fig．7 Stress－ strain curves of concrete

在剪力墙两侧各有一个箍筋约束区，按约束混凝土处理［17］。约束混凝土的特性与普通混凝土有所不同，其受压时延性与强度都有很大提高，而受拉时无明显影响。约束混凝土应力应变全曲线与普通混凝土的应力应变全曲线形状一致，约束混凝土的压应力峰值及屈服应变计算公式如下［18－19］:

式中，fcc，εcc为约束混凝土受压应力峰值与屈服应变;fc0，εc0为普通混凝土受压应力峰值与屈服应变;λv是配箍特征值(λv= ρ fyh/fc0，ρ为体积配箍率，fyh为箍筋屈服强度)。

添加短纤维的超高韧性水泥基复合材料虽然性能较普通混凝土有所改变，但仍属于混凝土材料范畴，在选择UHTCC本构模型时，本文仍采用Darwin－Pecknold二维本构关系模型，只在等效单轴应力应变曲线上发生改变。相较普通混凝土，UHTCC拉应力峰值未有明显提高，而延性大大增加［20］，受压应力峰值也无明显影响，屈服应变稳定在0．005左右，高于普通混凝土的极限压应变值［21－22］。本文对UHTCC本构关系的选取如图7虚线所示，受拉区取理想弹塑性模型，拉应力峰值对应的应变与约束混凝土相同，其极限拉应变取0．03。考虑到UHTCC材料的特性与边缘箍筋的约束作用，有关混凝土材料的本构关系取值列于表3中。其中，混凝土受拉应力应变参数参考《混凝土结构设计规范》(GB 50010—2010)［23］。

表3 混凝土参数Table 3 Parameters of Concrete

因UHTCC材料种类众多，受力性能差别很大，本文的UHTCC剪力墙是在原剪力墙的基础上改进而来，无具体的 UHTCC，仅模拟研究UHTCC对剪力墙性能的一般影响。根据超高韧性材料的有关实验研究，本文的UHTCC本构关系曲线不改变受拉及受压峰值应力，只对其受压屈服应变及受拉开裂后的特性进行改变。这体现了UHTCC的主要力学性能特征，因此是合理的。

钢筋本构关系采用双折线强化模型，强化段切线模量取初始模量的1%，未考虑钢筋断裂情况，所有钢筋的屈服应力及应变取值也都在表4中详细说明。

表4 钢筋材料参数Table 4 Parameters of reinforcement

4．2．3 模拟结果

图8和图9分别给出了两种型号的普通混凝土剪力墙与超高韧性水泥基复合材料剪力墙侧向承载力试验曲线以及VFIFE和ABAQUS的模拟曲线。从两张图中可以看到，VFIFE与ABAQUS在弹性段对剪力墙侧向承载力的计算结果与试验曲线基本符合。在非线性阶段，VFIFE对剪力墙的模拟结果与试验曲线较为一致，相较ABAQUS，VFIFE模拟剪力墙侧向承载力的下降段更为平缓。显然，在弹性段，VFIFE和 ABAQUS有同样优异的表现，而在线性阶段，VFIFE对剪力墙的模拟稍好于ABAQUS。

图8 SW1－1和SWU1－1侧向承载力曲线Fig．8 Lateral bearing capacity of SW1 －1 and SWU1－1 wall

图9 SW6－3和SWU6－3侧向承载力曲线Fig．9 Lateral bearing capacity of SW6 －3 and SWU6－3 walls

从VFIFE和ABAQUS对超高韧性水泥基复合材料对剪力墙的模拟结果中可知，将原墙两侧暗柱部分替换成超高韧性水泥基复合材料后，SWU1－1的承载力有比较明显的增加，而延性变化并不明显。SWU6－3的延性有比较明显的增加，承载力稍微有一些增加。由此可以看出，不同轴压力下，把剪力墙边缘替换成UHTCC材料对剪力墙的影响也不同，在轴压力较低时，剪力墙的承载力提升较为明显，而高轴压力时，对剪力墙的延性提升更为突出。

图10(a)和图10(b)是普通剪力墙在顶部侧向位移为15 mm时的Mises应力云图，剪力墙侧向位移15 mm时，其侧向承载力在峰值点偏右一点，可以明显看到剪力墙开裂区域及高应力区域。从应力云图可以看出，左侧区域大面积开裂，裂缝区域斜向下发展，右下角区域受压破坏，与实际情况基本一致。图10(c)和图10(d)分别是相同点的的两片UHTCC剪力墙Mises应力云图，和普通剪力墙Mises应力云图相比，两片UHTCC剪力墙的受拉开裂区域明显增大，右下角受压高应力区域减小，破坏区域减少。这说明，UHTCC剪力墙的裂缝更多，裂缝平均宽度也更小。

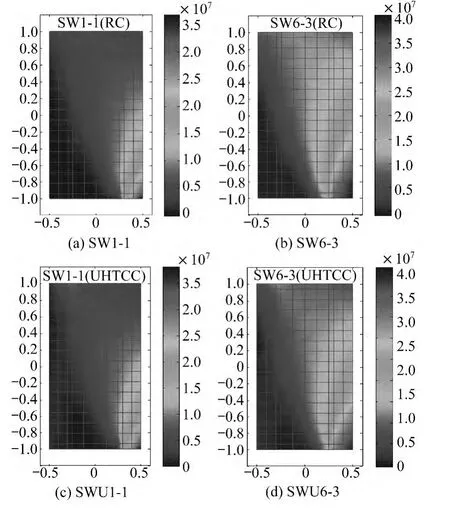
图10 顶端侧向位移15 mm时剪力墙Mises应力云图(单位:N/m2)Fig．10 Mises stress contour of walls at 15 mm(N/m2)

5 分析结果与讨论

由普通剪力墙与UHTCC剪力墙的模拟结果对比分析可知:

(1)在破坏模式上，采用超高韧性水泥基复合材料后，总体破坏模式并未发生非常大的改变，但剪力墙总体应力分布有所改变，受压高应力区域面积有所减少，破坏面积也相应减少。

(2)在抗侧承载力方面，新材料提升作用并不明显，这与UHTCC材料的本构关系设定有关(不改变受拉、受压应力峰值)。在原钢筋混凝土剪力墙承载力开始下降时，UHTCC剪力墙侧向承载力未出现明显下降，下降速率缓慢，变形有持续增加的趋势，由此说明UHTCC剪力墙后期工作性能有较大改善，延性增强，塑性变形能力增强，抗震性能更加优异。

(3)在受拉裂缝开展模式方面，UHTCC剪力墙受拉开裂区域增大，裂缝数量增多增密，裂缝平均宽度减小。

由ABAQUS和VFIFE的模拟结果对比分析可知，在弹性段，两者表现一致，都能很好地模拟剪力墙承载力－位移曲线弹性段，而在非线性阶段，VFIFE模拟结果要更加贴近试验曲线。

6 结论

本文简单介绍了向量式理论及向量式有限元板单元程序编制过程，利用自开发程序VFIFE以及ABAQUS，对比分析了普通钢筋混凝土剪力墙与超高韧性水泥基复合材料剪力墙拟静力推覆过程，并与试验值作以比较，由此得出如下几个结论:

(1)向量式有限元在模拟混凝土剪力墙的非线性行为时能够取得与试验结果较为一致的结果。

(2)UHTCC剪力墙的刚度降低并不明显，并且开裂后期的工作性能得到有效改善，低轴压力时，剪力墙的承载力提升作用明显，而高轴压力时，剪力延性提升作用更加突出。

(3)超高韧性水泥基复合材料剪力墙的受拉开裂区域增大，裂缝更加细密。

超高韧性水泥复合材料的弹性模量比一般混凝土材料都要低很多，应力峰值一般都有较大程度的提高，本文中对超高韧性水泥基复合材料本构关系的选取仍有很多不足，其初始弹性模量、应力－应变曲线、损伤量的计算等需要更好的考虑。UHTCC总体是偏软的，延性远好于普通混凝土材料，采用UHTCC替换剪力墙两侧暗柱，在保证剪力墙的刚度情况下，改善剪力墙后期工作性能，增强了剪力墙的延性，提升了剪力墙构件的抗震性能，因此具有良好的应用前景。

［1］ 徐世烺，李贺东．超高韧性水泥基复合材料研究进展及工程应用［J］．土木工程学报，2008，41(6):45-60．Xu Shilang，Li Hedong．Ultra high toughness cementitous composites research progress and application engineering［J］．Civil Engineering Journal，2008，41(6):45-60．(in Chinese)

［2］ Li V C．Advances in ECC research［J］．ACI Special Publication on Concrete:Material Science to Applications，2002，SP 206-23:373-400．

［3］ Li V．C，Leung C K Y．Steady state and multiple cracking of short random fiber composites［J］．Journal of Engineering Mechanics，ASCE，1992，188(11):2246-2264．

［4］ 章红梅，吕西林．一种基于半预制超韧性钢筋混凝土的叠合剪力墙．发明申请号:201510090061．6，发文日:2015-02-28．Zhang Hongmei，Lu Xilin．One semi-recast ultra high toughness reinforced concrete laminated shear wall［P］．Patent application No．:201510090061．6，The date of issuance:2015-02-28．

［5］ Ting E．C，Shih C，Wang Y K．Fundamentals of a vector form intrinsic finite element:Part1 basic procedure and a plane frame element［J］，Journal of Mechanics，2004，20(2):113-122．

［6］ 丁承先，段元锋，吴东岳．向量式结构力学［M］．杭州:浙江大学出版社，2012．Ting Chengxian，Duan Yuanfeng，Wu Dongyue．Vector mechanics of structure［M］．Hangzhou:Zhejiang University Press，2012．(in Chinese)

［7］ Ting E C，Wu T Y，Wang C Y，et al．Motion analysis and vector form intrinsic finite element［R］．Report NO．cber2006-w-001，National Central University，2006．

［8］ Ting E C，Shih C，Wang Y K．Fundamentals of a vector form intrinsic finite element:Part2 plane solid element［J］，Journal of Mechanics，2004，20(2):123-132．

［9］ Shih C，Wang Y K，Ting E C．Fundamentals of a vector form intrinsic finite element:Part3 convected material frame and examples［J］，Journal of Mechanics，2004，20(2)，133-143．

［10］ Wu T Y，Lee J J，Ting E C．Motion analysis of struc-tures for flexible multi-body systems:planar motion of solids［J］．Multibody System Dynamics，2008，20(3):197-221．

［11］ Dong Yuguang，Lu Xilin．Study on axial compression ratio calculation and limit value for steel reinforced concrete walls［J］．Journal of Earthquake Engineering and Engineering Vibration，2007，27(1)，80-85．

［12］ Zhang Hongmei，Lu Xilin，Li Jianbao，et al．Cyclic load experiment study on the laminated composite RC walls with different concrete ages［J］．Structural Engineering and Mechanics，2010，36(6)，745-758．

［13］ Zhang Hongmei，Lu Xilin and Wu Xiaohan．Experimental study and numerical simulation of the reinforced concrete walls with different stirrup in the boundary element［J］．Journal of Asian Architecture and Building Engineering，2010，17(2)，447-454．

［14］ 江见鲸，陆新征，叶列平．混凝土结构有限元分析［M］．北京:清华大学出版社，2006．Jiang Jianjing，Lu Xinzheng，Ye Lieping．Finite element analysis of concrete structures［M］．Beijing:Tsinghua University Press，2006．(in Chinese)

［15］ Darwin D，Pecknold D A．Nonlinear biaxial stressstrain law for concrete［J］．ASCE，Journal of the Engineering MechanicsDivision， 1977， 103(2):229-241．

［16］ Hillerborg A，Modeer M，Peterson P E．Analysis of crack formation and crack grouth in concrete by means of fracture mechannics and finite element［J］．cement and concrete research，1976，6(6):773-782．

［17］ Zhang Hongmei，Lu Xilin，Lu Liang．Influence of boundary element on seismic behavior of reinforced concrete shear walls［J］．Journal of Earthquake Engineering and Engineering Vibration，2007，27(1)，92-98．

［18］ 钱稼茹，程丽荣，周栋梁．普通箍筋约束混凝土柱的中心受压性能［J］．清华大学学报(自然科学版)，2002，42(10):24-36．Qian Jiaru，Cheng Lirong，Zhou Dongliang．The compression performance in the center of the ordinary concrete column stirrup constraint［J］．Tsinghua University Journal(Natural Science)，2002，42(10):24-36．(in Chinese)

［19］ 邢秋顺，翁义军，沈聚敏．约束混凝土应力应变全曲线的实验研究［C］．烟台:约束混凝土御普通混凝土强度理论及应用学术讨论会，1987．Xing Qiushun，Wen Yijun，Shen Jumin．Experimental study on complete stress-strain curves of confined concrete［C］．Yantai:Proc Symposium on Strength Theory and Its Application of Confined Concrete and Plain Concrete，1987．(in Chinese)

［20］ 徐世烺，李贺东．超高韧性水泥基复合材料直接拉伸试验研究［J］．土木工程学报，2009，42(9):32-41．Xu Shilang，Li Hedong．Uniaxial tensile experiments of ultra-high toughness cementitous composite［J］．Civil Engineering Journal，2009，42(9):32-41．(in Chinese)

［21］ 徐世烺，蔡向荣，张英华．超高韧性水泥基复合材料单轴受压应力-应变全曲线试验测定与分析［J］．土木工程学报，2009，42(11):79-85．Xu Shilang，Cai Xiangrong．，Zhang Yinghua．Experiment measurement and analysis of the axial compressive stress-strain curve of ultra high toughness cementitious composites［J］．Civil Engineering Journal，2009，42(11):79-85．(in Chinese)

［22］ 蔡向荣．超高韧性水泥基复合材料基本力学性能和应变硬化理论过程分析［D］．大连:大连理工大学，2010．Cai Xiangrong．The basic mechanical performance and strain hardening progress theoretical analysis of ultra high toughness cementitious composites［D］．Dalian:Dalian University of Technology，2010．(in Chinese)

［23］ 中华人民共和国住房和城乡建设部．GB 50010—2010混凝土结构设计规范［S］．北京:中国建筑工业出版社，2010．Ministry of Housing and Urban-Rural Development of the People＇s Republic of China．GB 50010—2010 Code for concrete structure design［S］．Beijing:China Architecture and Building Press，2010．(in Chinese)