装配式简支钢－混组合小箱梁桥荷载向分布系数的研究

李瑞琪 袁万城 高 康 王建国 郭军军

(同济大学土木工程防灾国家重点实验室，上海200092)

1 引言

自从装配式钢－混凝土组合小箱梁桥问世以来，凭借其优良的力学性能得到桥梁设计师的广泛青睐，在城市立交和高架建设中发挥着越来越重要的作用。近年来组合小箱梁桥的承载力计算体系己比较完善，但是有关其在活载作用下的横向分布系数计算仍然存在不足，这在一定程度上限制了该桥型经济效益的发挥。清华大学聂鑫等人［1］针对连续组合梁桥的横向受力分布性能和计算方法进行了理论研究;钟小军、赵中兴等人［2～3］研究了混凝土小箱梁桥的横向分布系数理论计算方法，并通过与实测结果的校核找出合适的近似计算方法;倪章军等人［4］针对新型GFRP组合梁桥荷载横向分布系数影响参数进行了研究，提出相应优化设计原则。以上相关研究的研究对象与钢－混组合小箱梁桥存在一定差异，故其得到的结论可以为组合小箱梁桥横向分布系数提供参考，但具体规律还需针对该桥型的横向受力分布进行进一步的研究。

目前常用的横向分布系数理论计算方法主要有刚性横梁法、修正刚性横梁法以及杠杆原理法等［5］，由于在推导时进行了各种假设，因此理论计算方法均存在不可避免的较大误差。利用MIDAS或ANSYS中有限元模型模拟的方法所得结果比较准确，但过程过于繁琐，因此实际工程中分析荷载横向分布时常使用梁格法。梁格法就是用等效的梁格代替桥梁上部结构的一种方法，将分布在空间板(梁)上每一区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内，实际结构的纵向刚度集中于纵向主梁构件内，横向刚度集中于横隔梁及虚拟横梁构件内，在承受相同荷载时，要求两者的挠曲相等，内力也是相等的［6］。梁格单元截面特性的正确计算和构件间连接关系的正确模拟是保证计算精度的关键，对此目前尚没有确定的方法。除此之外，有关横向联系梁间距等参数对组合梁桥横向分布的影响也需进一步的研究。

本文针对某装配式简支钢－混组合箱梁桥展开讨论，利用MIDAS Civil中的板单元建模功能建立模型，研究各参数(横向联系梁间距以及刚度等)对组合箱梁桥横向受力分布的影响程度，接下来使用梁格法和其他常见计算方法(刚性横梁法等)计算该桥的横向受力分布系数，与板单元模型所得结果进行对比，对各种理论计算方法的适用性进行了评价，同时针对梁格法参数取值提出了相应建议。

2 桥例介绍

本文分析的桥例为一座装配式简支钢－混组合箱梁桥中的一跨。跨径:30 m;设计荷载:公路－Ⅰ级;桥面布置:0．5 m×2(防撞护栏)+15 m(包含紧急停车带在内的行车道)=16 m;主梁形式:5榀间距3．2 m的开口槽型钢箱梁(Q345);桥面板及铺装:22 cm厚预制混凝土桥面板(C50)，10 cm厚沥青混凝土铺装层;横向连系梁:横向联系梁采用三块钢板焊接而成的工字截面短梁，桥梁横断面图见图1。

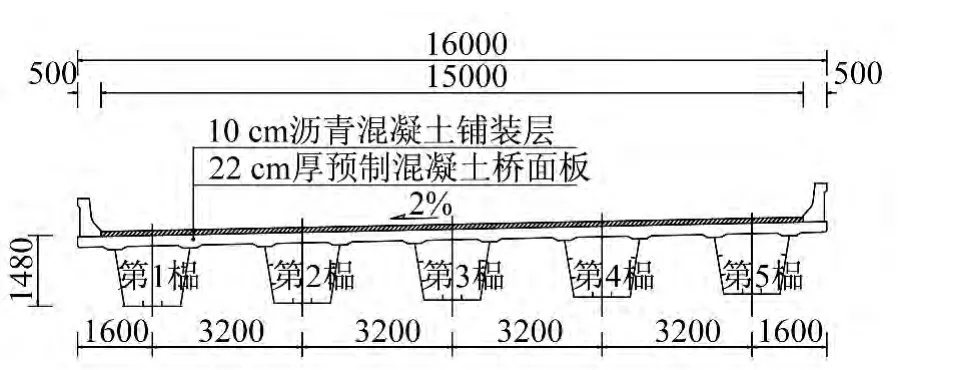
图1 桥例横断面图(单位:mm)Fig．1 The cross section of the girder bridge(Unit:mm)

3 横向受力分布影响参数分析

利用MIDAS中的板单元建模功能，建立板单元模型，其中横向连系梁与纵梁间设为刚性连接(共点)。按照图2所示施加汽车荷载，考虑到组合箱梁桥的桥面板发挥了一定的横向联系作用，因此该桥空间受力性能较强，故图2所示汽车荷载布置对于左数第1榀、2榀、3榀梁均为最不利布置荷载。

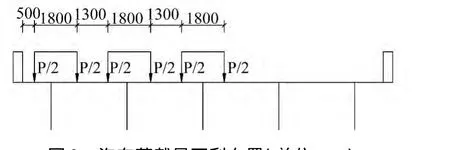
图2 汽车荷载最不利布置(单位:mm)Fig．2 The most disadvantageous arrangement(Unit:mm)of the vehicle load

为了研究不同参数(横向连系梁间距、桥面板铰接缝、桥面板厚度等)对组合箱梁桥横向受力分布的影响，采用单一变量的研究方法，建立表1－表3中的对比模型，求取汽车荷载下各榀梁跨中位移fk，并按照下式计算横向分布系数［7］。

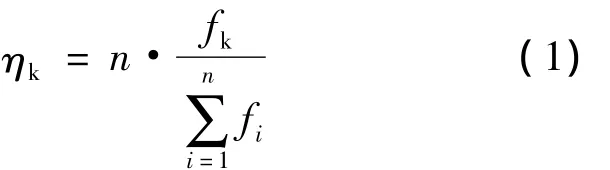
3．1 横向联系梁间距对荷载横向受力分布影响

为了研究横梁间距对组合梁桥横向受力分布情况的影响，在MIDAS中建立系列板单元对比模型，横梁间距分别为15 000 mm(3根横梁)、7 500 mm(5根横梁)、6 000 mm(7根横梁)、3 750 mm(9根横梁)、2 000 mm(15 根横梁)，另建立了无横梁模型与之对比。

表1 不同横隔梁间距下各榀梁汽车荷载下的跨中位移值及横向分布系数Table 1 The mid-span displacement and the transverse distribution coefficient in different spacing of diaphragms

分析表1发现，随着横向连系梁间距减小，各榀梁横向受力分布趋于均匀，但变化幅度很小。因此在组合箱梁桥中，横向连系梁的主要作用主要作用是增强施工阶段钢箱梁稳定性，并非用以协调各榀梁受力，这是组合梁桥与混凝土梁桥极为不同的一点，对于横隔梁设计具有指导性意义。

3．2 桥面板厚度对荷载横向受力分布影响

为了研究桥面板厚度对组合梁桥横向受力分布情况的影响，在MIDAS中建立系列板单元对比模型，为使研究更具实用意义，板厚取常见值，这里分别取150 mm，200 mm，250 mm，300 mm。

分析表2发现，混凝土板厚在150 mm到300 mm间变化时，各榀梁横向分布系数变化不大，但跨中位移值随板厚增大而显著减小，这是因为混凝土板厚的增加显著提高了组合截面刚度值。

3．3 桥面板铰接缝对荷载横向受力分布的影响

本桥例施工时采用对称拼装的方法，板与板间的纵向接缝采取刚接方式;横向接缝采取铰接方式(图3)。

表2 不同板厚下各榀梁在汽车荷载作用下跨中位移值及横向分布系数Table 2 The midspan displacement and the transverse distribution coefficient in different thickness of the concrete deck

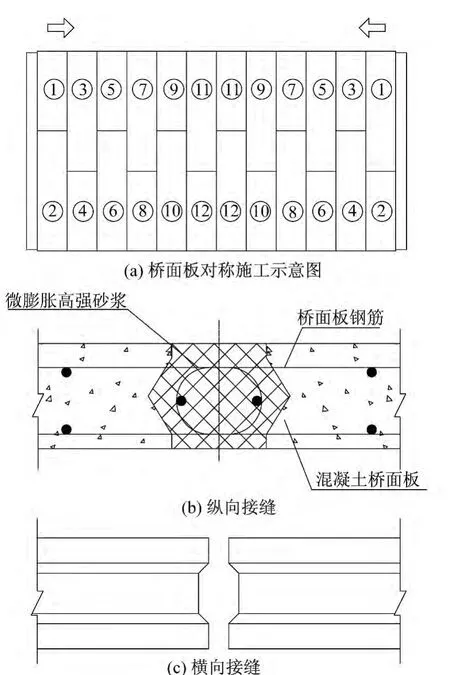
图3 对称施工示意图及接缝大样图Fig．3 The schematic drawing of construction and the detail drawing of the joints

为研究横向铰接缝对横向受力分布的影响，设置两组对比模型，模型1通过释放板端约束以模拟铰缝，模型2不再模拟铰缝。

表3 不同铰接缝设置情况各榀梁车荷载作用下跨中位移值及横向分布系数Table 3 The midspan displacement and the transverse distribution coefficient in different arrangement of hinge joint

分析表3发现桥面板铰接缝的模拟与否对组合梁桥横向受力分布影响不大，因此在板单元模型建立时可以忽略不计。

4 横向受力分布系数计算方法

4．1 各种计算方法适用性评价

分别使用偏心压力法、修正偏心压力法，以及MIDAS中的板单元建模(图4)和梁板建模(图5)的方法求取该桥例在图2所示汽车荷载作用下各榀钢箱梁跨中下底板下缘拉应力数值，并据此求取各榀梁跨中横向分布系数(图6、图7)。

图4 MIDAS中建立板单元模型Fig．4 The plate-element model in MIDAS

图5 MIDAS中建立梁板模型Fig．5 The beam-plate model in MIDAS

其中修正偏心压力法计算抗扭修正系数时可代入钢箱梁相应几何参数进行计算;板单元模型建立时，钢梁和混凝土桥面板全部以板单元建立，两者之间通过共点模拟剪力键的作用;梁板模型中主梁及横向连系梁以梁单元模拟，并通过共点模拟主梁和横梁间的刚接连接，混凝土桥面板以板单元模拟，两者之间通过刚接模式的弹性连接单元实现剪力键的模拟。

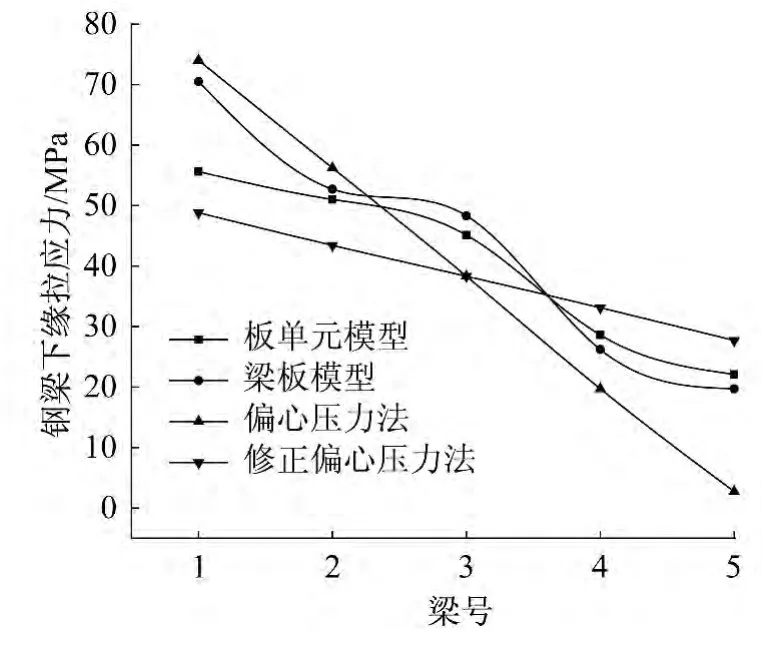
图6 不同计算方法所得各榀梁跨中下缘拉应力比较Fig．6 The mid-span tensile stress under the vehicle load with different methods

考虑到1号边梁受力最为不利，对设计起决定性作用，因此就1号边梁受力进行比较，偏心压力法计算结果比实际结果大30%，修正偏心压力法计算结果比实际结果小15%，因此偏心压力法是一种偏于保守的计算方法，而修正偏心压力法是一种偏于不安全的计算方法。梁板建模所得结果介于板单元模型与偏心压力法结果之间，是一种偏安全且简便的方法，可以考虑使用。

图7 不同计算方法所得各榀梁横向分布系数比较Fig．7 The mid-span transverse distribution coefficient with different methods

4．2 梁格法参数讨论

根据与混凝土梁桥梁格法参数设定进行类比［8～9］，对组合箱梁桥参数做如下规定:

(1)纵梁截面特性:为了保证纵向刚度的一致，纵梁截面应该取组合梁截面(图8)，考虑到沥青混凝土铺装层对横向受力分布几乎不起作用，因此混凝土板厚取220 mm。利用MIDAS的组合梁截面特性计算功能即可算得组合梁截面几何特性及力学特性值，如截面惯性矩、抗弯刚度等。

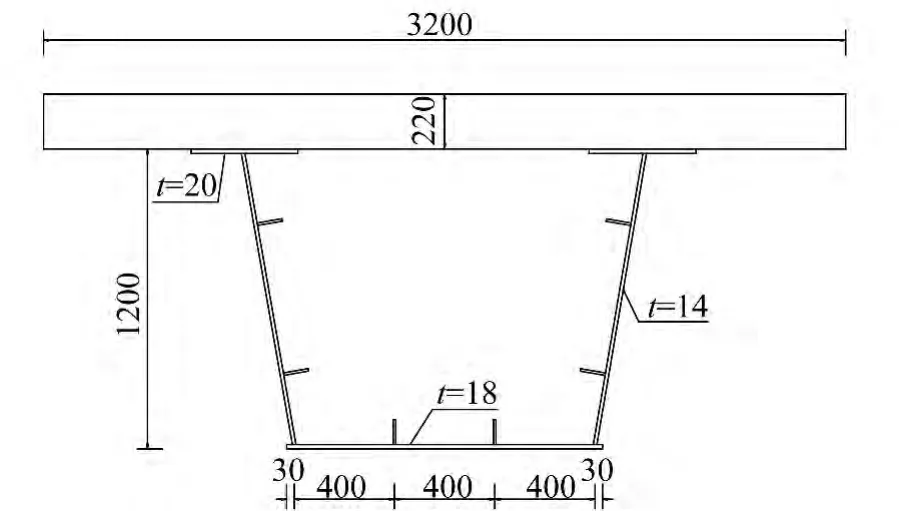
图8 纵梁截面图(单位:mm)Fig．8 The cross section of the girder(Unit:mm)

(2)横向连系梁:有研究表明［1］，在组合箱梁桥的横向受力分布中，桥面板承担大部分的作用，横向连系梁承担作用很少。因此梁格法建模时为保证传力途径清晰明确，并且避免局部应力集中现象，可不设横向连系梁。

(3)虚拟横梁:在实际结构中，桥面板作为整体连接着各榀钢梁，因此各榀钢梁间的协同工作性能比较强，故虚拟横梁与主梁间的连接使用共点方式;为了便于调整截面刚度，截面形状选择矩形，并且依照以往梁格法经验，将矩形截面的高h设置为混凝土桥面板的厚度H=220 mm，而截面的宽B/mm作为可变参数展开讨论，同时虚拟横梁间距Δ也作为可变参数参与下面的讨论。

梁格法建立模型如下(图9)，按照图2所示施加汽车荷载，不断变化B与Δ的数值，求取各榀梁跨中位移，与板单元模拟所得结果进行对比。

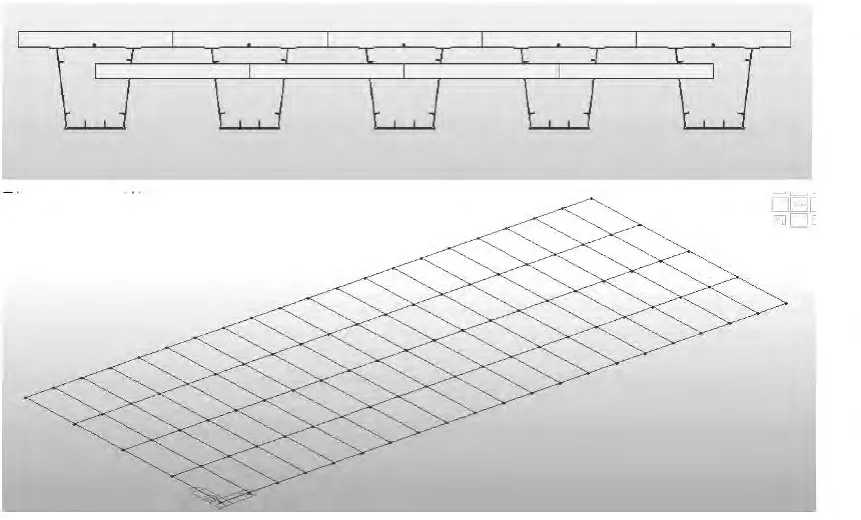
图9 梁格法模型Fig．9 The grillage model in MIDAS

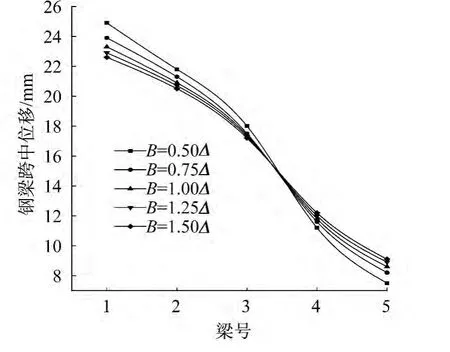
图10 B/Δ变化过程中各榀梁汽车荷载作用下跨中位移变化Fig．10 The mid-span displacement under the vehicle load in different value of B/Δ

由图10可见，在 B由0．5Δ变化到1．5Δ的过程中横向受力分布变化并不大，1号边梁的跨中挠度值变化幅度不超过10%。出于安全考虑，应使近荷载一侧边梁计算所得应力及挠度值更大一些，故可以取B=Δ，此时梁格法结果比板壳元结果大10%左右，在保证了结构安全的同时，使结果更加准确，大大减少了不必要的经济损失。

4 结论

本文主要研究了各参数(横向连系梁间距以及刚度等)对装配式简支组合箱梁桥横向受力分布的影响，接下来对各种理论计算方法的适用性进行了评价，同时针对梁格法参数取值提出了相应建议，得到以下三点结论:

(1)横向连系梁间距、桥面板铰接缝设置、预制桥面板厚度等因素对简支组合箱梁桥横向受力分布性能影响均不大，在组合箱桥梁设计中不能盲目地通过增加板厚或减小横梁间距来使各榀梁受力更均匀，这种做法既不经济又达不到预期效果。

(2)偏心压力法和梁板建模方法计算所得最不利边梁拉应力比实际情况大25%以上，是偏于保守的计算方法。

(3)梁格法求取简支组合箱梁桥横向受力分布时，纵梁截面应选择组合截面，虚拟横梁材料应选择混凝土，虚拟横梁截面形状可选择矩形，矩形高度取桥面板厚度，矩形宽取虚拟横梁间距值(B=Δ)，虚拟横梁与纵梁的连接处应选择共点的刚接方式。计算所得最不利边梁的跨中最大位移值比三维有限元模型运算结果略大5%～10%，在保障安全性的同时避免了不必要的经济损失。

［1］ 聂鑫，樊健生，付裕．箱梁截面连续组合梁桥的荷载横向分布［J］．清华大学学报，2000，49(12):1931-1938．Nie Xin，Fan Jiansheng，Fu Yu．Transverse load distribution on box section continuous composite steel-concrete bridge［J］．Journal of Tsinghua University，2000，49(12):1931-1938．(in Chinese)

［2］ 钟小军．装配式小箱梁桥横向分布系数探究［J］．中国市政工程，2013，(2):17-19．Zhong Xiaojun，A discussion of load transverse distribution coefficients of fabricated small box girder bridge［J］．China Municipal Engineering，2013，(2):17-19．(in Chinese)

［3］ 赵兴中，马琳．预制装配式小箱梁桥横向分布计算方法的研究分析［J］．湖南交通科技，2009，35(2):94-97．Zhao Xingzhong，Ma Lin．Study and analysis of transverse distribution method of precast fabricated smallbox beam bridge［J］．Hunan Communication Science and Technology，2009，35(2):94-97．(in Chinese)

［4］ 倪章军，范立础，李建中．新型GFRP组合梁桥荷载横向分布系数计算［J］．桥梁建设，2007，(2):51-54．Ni Zhangjun，Fan Lichu，Li Jianzhong．Calculation of load transverse distribution factors of new type of GFRP composite beam bridge［J］．Bridge Construction，2007，(2):51-54．(in Chinese)

［5］ 范立础．桥梁工程［M］．北京:人民交通出版社，2012:225-230．Fan Lichu．Bridge engineering［M］．Beijing:China Communications Press，2012:225-230．(in Chinese)

［6］ 张剑超．关于桥梁荷载横向分布系数的研究［D］．武汉:武汉理工大学，2011．Zhang Jianchao．Study on load transverse distribution coefficient of bride［D］．Wuhan:Wuhan University of Technology，2011．(in Chinese)

［7］ 韦立林，王文宁，王建军．简支梁桥荷载试验横向分布系数分析方法［J］．广西大学学报，2007，32(2):183-185．Wei Lilin，Wang Wenning，Wang Jianjun．The method for analyzing transverse distribution factors in load test of simple supported bridge［J］．Journal of Guangxi U-niversity，2007，32(2):183-185．(in Chinese)

［8］ 黄立浦，谭海亮，曹素功．装配式简支 T形梁桥横向分布系数的研究［J］．长沙大学学报，2011，25(5):12-14．Huang Lipu，Tan Hailiang，Cao Sugong．A study of the lateral distribution coefficient for fabricated simply supported T-beam bridge［J］．Tournal of Changsha U-niversity，2011，25(5):12-14．(in Chinese)

［9］ 葛俊颖，丁啸宇．梁格法分析铰接板梁桥虚拟横梁刚度的取值研究［J］．公路，2010，(4):103-105．Ge Junying，Ding Xiaoyu．Grillage analysis of the hinged plate girder bridge virtual beam stiffness values［J］．Highway，2010，(4):103-105．(in Chinese)