竖向构件布置对梁式转换层结构刚度的影响
陈关平 张拥军 王金涛 李乾龙 刘金强,2
(1.青岛理工大学土木工程学院,青岛266033;2.山东建筑大学土木工程学院,济南250101)
1 引言
随着社会发展,人们对生活的多样化不断追求不断提高,现代高层建筑向多功能和综合用途发展,在同一竖直线上,顶部楼层布置住宅、旅馆,中部楼层作办公用房,下部楼层作商店、餐馆和文化娱乐设施。不同用途的楼层,需要大小不同的开间,采用不同的结构形式。建筑要求上部小开间的轴线布置、较多的墙体,中部办公用房要小的和中等大小的室内空间,下部公用部分,则希望有尽可能大的自由灵活空间,柱网要大,墙尽量少。这种要求与结构的合理、自然布置正好相反,因为结构下部楼层受力很大,即正常应当下部刚度大、墙多、柱网密,到上部逐渐减少。为了满足建筑功能的要求,结构必须以与常规方式相反进行布置,上部小空间,布置刚度大的剪力墙,下部大空间,布置刚度小的框架柱。为此,必须在结构转换的楼层设置转换层,称结构转换层[1]。
高层转换层结构中,设置的转换层破坏了建筑物高度方上的均匀性,转换层竖向承力构件不连续,导致传力路线突然改变、刚度突变、应力集中。由于在转换层处的结构刚度突变,其抗震性能相对较差,在满足承载力要求的同时要进一步控制结构的侧向刚度比,保证结构刚度的均匀性,减小地震效应。山东建筑大学傅传国对高层建筑托柱转换结构力学的特点做出分析与比较[2];合肥工业大学王宾通过改变落地剪力墙的数量和厚度对框支剪力墙结构中剪力墙合理数量做出了研究[3];同济大学黄勤勇、吕西林通过改变底部剪力墙的厚度对转换层上、下刚度比对框支剪力墙结构抗震性能的影响做相应的研究[4]。祁勇、朱慈勉基于Push-over方法的框支短肢剪力墙转换层结构做出相应的弹塑性分析[5]。张叶田、吴云海对高层建筑转换层结构方案的选择做出相应研究[6]。
2 计算模型
青岛市某梁式转换层高层建筑,采用7度抗震设防烈度,基础作用在坚硬的花岗岩上,无地下室,基础埋深较浅,取基础顶面作为上部结构的嵌固部位。该结构共30层,一层层高5 m,其余各层3.3 m。纵向和横向轴网间距为6 m。本文采用PMCAD软件建立了6个模型,每个模型共30层97.4 m,且转换层位于第一层,采用梁式(梁托墙或柱)转换。每个模型的转换层都位于一层,由支撑框架和落地剪力墙组成,层高5 m,结构平面布置图如图1所示。

图1 转换层结构平面布置结构(单位:mm)Fig.1 Conversion layer structure layout structure(Unit:mm)
转换层上部为框架剪力墙结构,纵向和横向轴网间距为6 m,层高3.3 m,分别采用如图2—图7结构布置形式。本文以转换层上部结构剪力墙布置方式对结构的影响为研究目标,不考虑结构中电梯井筒及设备管道作为抗侧力构件对结构性能的影响。模型中剪力墙的布置方式为研究所用,不具有代表性,对于其他形式的转换层结构需要另行分析。
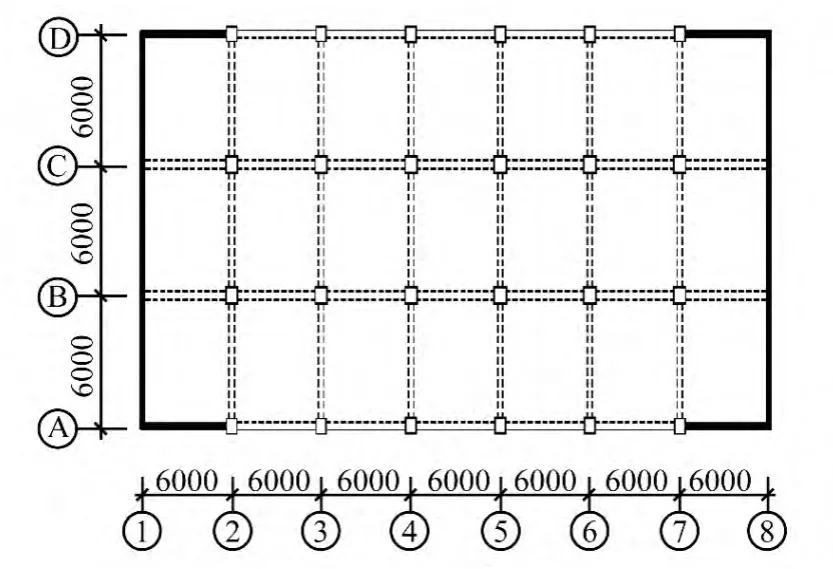
图2 模型1转换层上部结构(单位:mm)Fig.2 Model 1 superstructure conversion layer(Unit:mm)
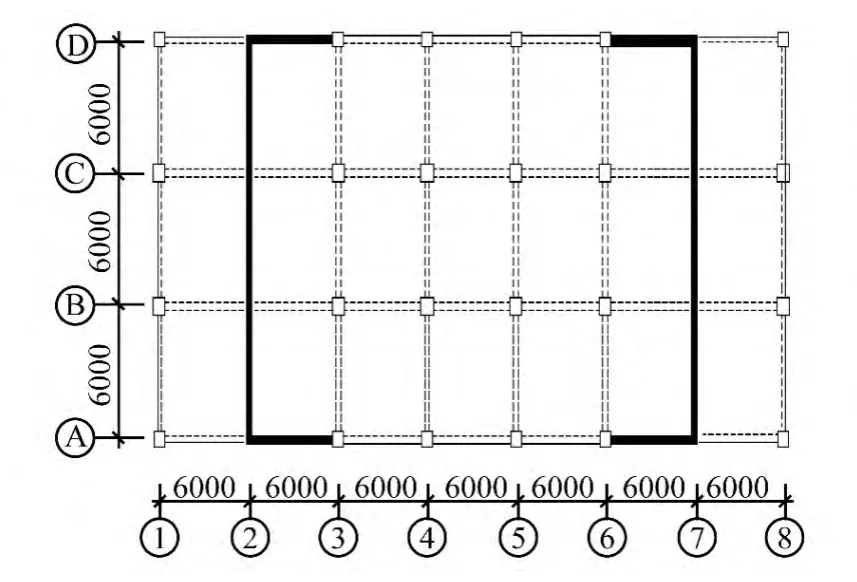
图3 模型2转换层上部结构(单位:mm)Fig.3 Model 2 superstructure conversion layer(Unit:mm)

图4 模型3转换层上部结构(单位:mm)Fig.4 Model 3 superstructure conversion layer(Unit:mm)
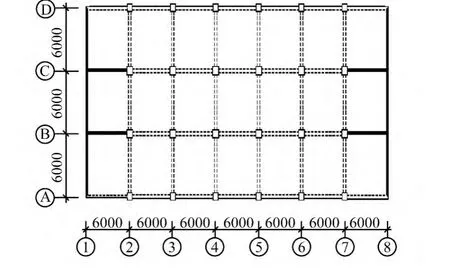
图5 模型4转换层上部结构(单位:mm)Fig.5 Model 4 superstructure conversion layer(Unit:mm)
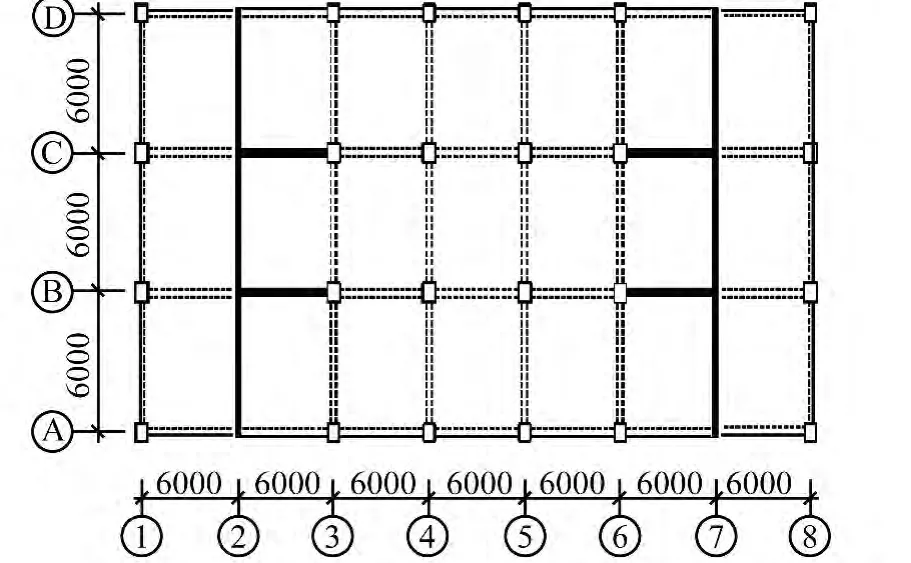
图6 模型5转换层上部结构(单位:mm)Fig.6 Model 5 superstructure conversion layer(Unit:mm)

图7 模型6转换层上部结构(单位:mm)Fig.7 Model 6 superstructure conversion layer(Unit:mm)
本文采用SATWE软件计算分析,SATWE软件中分地震剪力与地震层间位移比、剪切刚度比、剪弯刚度比三种计算方法。横向为X方向,纵向为Y方向。
转换层设置在1层、2层时,可近似采用转换层与其相邻上层结构的等效剪切刚度比γe1,表示转换层上、下层结构刚度的变化,γe1宜接近1,非抗震设计时不应小于0.4,抗震设计时不应小于0.5,可按下列公式计算[7]:

式中,G1,G2分别为转换层和转换层上层的混凝土剪变模量;A1,A2分别为转换层和转换层上层的折算抗剪截面面积;Aw,i为第i层全部剪力墙在计算方向的有效截面面积(不包括翼缘面积);Aci,j为第i层第j根柱的截面面积;hi为第i层的层高;hci,j为第i层或第j根柱沿计算方向的截面高度;hci,j为第i层第j根柱截面面积折算系数,当计算值大于1时取1。
梁式托柱转换结构不适合采用剪切刚度比计算[8],采用地震力与地震层间位移方法计算,并用剪弯刚度比进行补充计算[9]。
计算模型中转换层以下的结构布置保持不变,通过改变转换层上部结构中具有相同有效截面面积剪力墙的位置来分析不同位置剪力墙对转换层与其相邻上层结构的剪弯刚度比和侧向刚度比的影响。将模型分为三组,如图2—图7所示,用以分析竖向构件布置位置对X向结构刚度比以及性能变化的影响。将模型分为两组,如图2—图7所示,用以分析竖向构件布置位置对Y向结构刚度比以及性能变化的影响。当采用不同剪力墙位置模型与转换层上下刚度比的关系如表1所示。
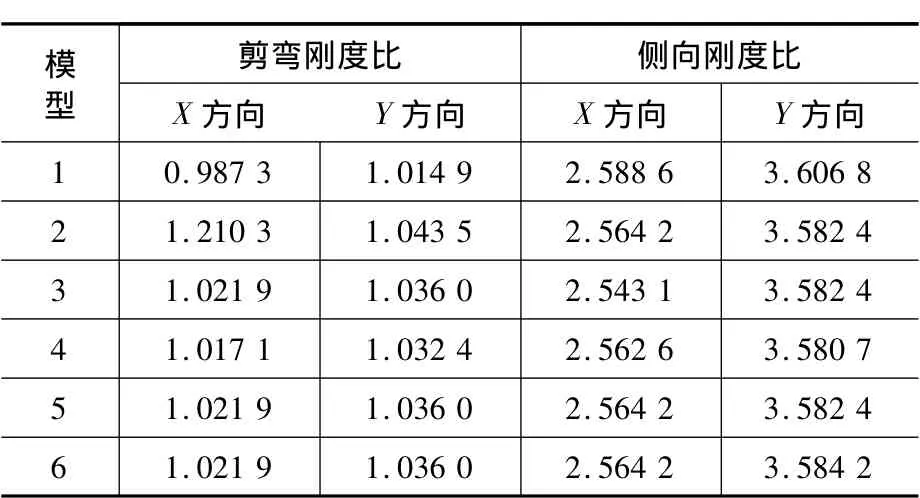
表1 刚度比Table 1 Stiffness ratio
由图2—图4和图5—图7两组模型来分析侧向刚度比和剪弯刚度比。
1)侧向刚度比
X方向(Xi表示第i个模型X方向的侧向刚度):

Y方向(Yj表示第j个模型Y方向的侧向刚度):
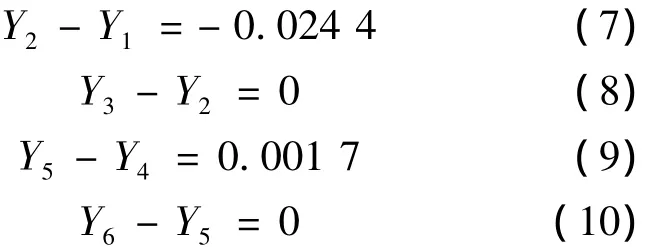
以上分析可得,随着转换层上部剪力墙由边跨向中间布置,结构横向和纵向的侧向刚度比整体逐渐减小。
由图2、图5,图3、图6和图4、图7三组数据可知,随着在转换层上部X、Y方向同时向中间布置,每组侧向刚度比对比如下:

由此可以看出,横向侧向刚度比逐渐减小。
2)剪弯刚度比对比,

由此可以看出,随着上部剪力墙由边跨向中间布置,剪弯刚度比逐渐减小。
由以上分析对比可得,随着转换层上部剪力墙由周边向中间逐跨布置,结构的侧向刚度逐渐减小,且减小的幅度逐渐降低。
3 计算结果分析
3.1 结构周期
由SATWE有限元分析软件计算分析得结构X、Y方向的平动周期及结构的扭转周期如表2所示。
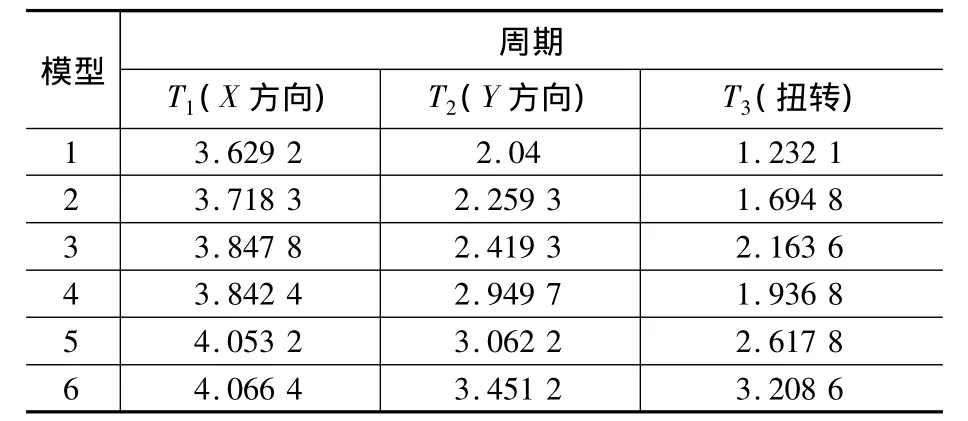
表2 结构周期Table 2 Structure period
3.1.1 竖向构件布置位置对X向结构周期变化的影响
由结构周期表2,分析竖向构件布置位置对X向结构刚度比以及性能变化的影响:
X方向平动周期(如图2、图3,图4、图5,图6、图7三组结构):
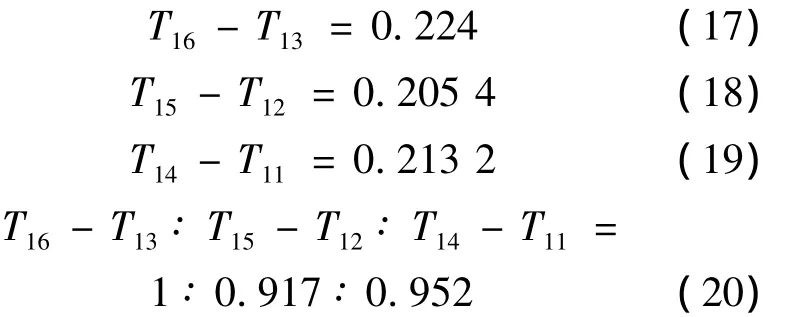
X 方向平动周期(如图 1、图 2、图 3,图 4、图5、图6两组结构):
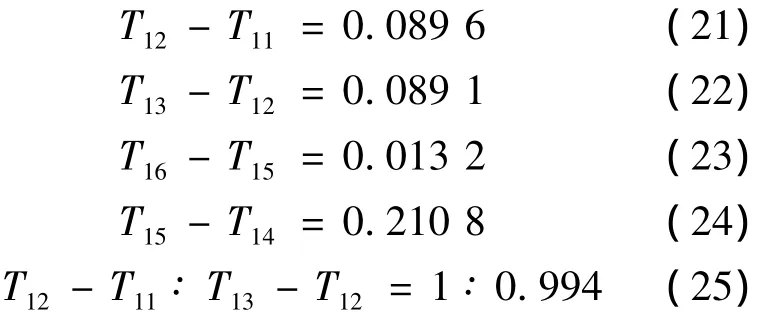
式中,Tij为右下标第一个数字i(1,2,3)表示对应X、Y、扭转方向结构周期,第二个数字 j(1,2,3,4,5,6)表示第j个模型。以下表示方式相同。例如,T16表示第6个模型X方向的平动周期。
由以上数据对比分析可得:随着竖向剪力墙逐渐向中间逐跨布置,结构的X方向平动周期T1逐渐增大且增加的幅度较均匀。其周期增加幅度比 1∶0.917∶0.952。
3.1.2 竖向构件布置位置对Y向结构周期变化的影响
由结构周期表2分析,分析竖向构件布置位置对Y向结构刚度比以及性能变化的影响:
Y 方向平动周期(如图 2、图 3,图 4、图 5,图6、图7三组结构):
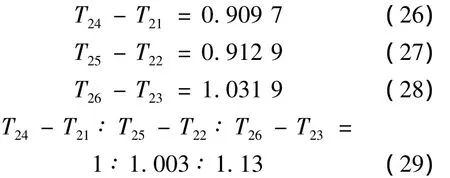
Y 方向平动周期(如图 2、图 3、图 4,图 5、图6、图7两组结构):
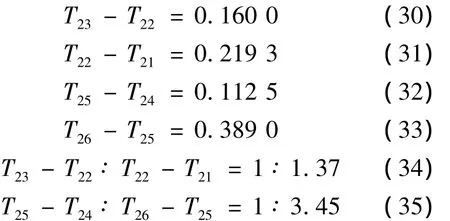
由上数据对比分析可得,随着竖向剪力墙向中间逐跨布置,整体结构的Y方向平动周期逐渐增大且增加的幅度较均匀。Y向周期T2增大幅度比值 1∶1.003∶1.13。
3.1.3 竖向构件布置位置对扭转周期变化的影响
扭转周期(如图2、图 3,图 4、图 5,图 6、图 7三组结构):


扭转周期(如图2、图3、图4,图5、图 6、图 7 两组结构):
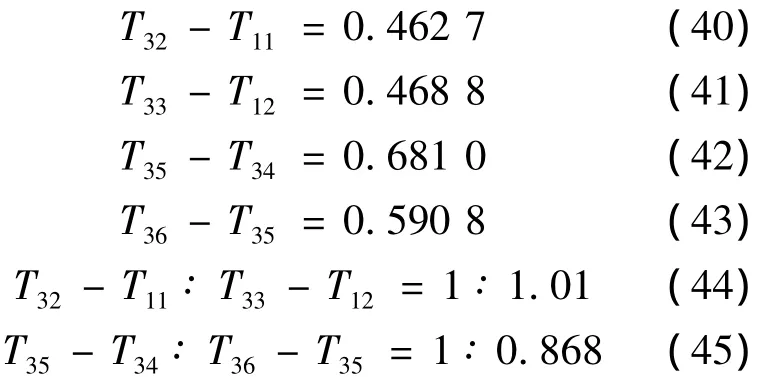
由以上数据对比分析可得,随着剪力墙由周围向中间逐跨布置,结构的扭转周期逐渐增大,且增大的幅度逐渐增大。扭转周期T3增大幅度比值 1∶1.31∶1.48。
3.1.4 结构扭转周期跟平动周期变化分析
结构扭转周期跟平动周期比较分析如下:

平均增长率:
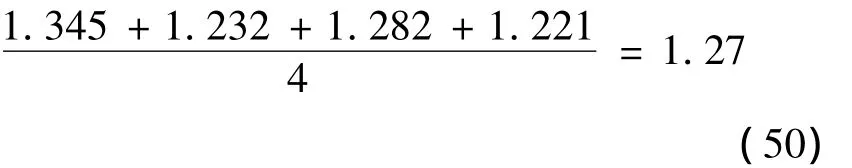
由上述数据对比分析可得,随着剪力墙由周围向中间逐跨布置,结构的扭转周期与平动周期的比值逐渐增大,其扭转周期跟平动周期比值的平均增长率是1.27。可以得出扭转周期比平动周期增大速率快,结构的扭转刚度比侧向刚度变化速率快。
3.2 结构侧移
随着剪力墙由周围向中间靠拢,结构的整体侧向刚度和扭转刚度都逐渐减小,从而使得结构的侧向位移逐渐增大,层间位移角增大。从顶点位移、层间最大位移角表3结构位移中可以看出:
随着剪力墙逐渐向中间布置,结构的顶点位移逐渐增大,层间位移角也逐渐增大。剪力墙在中间位置的时候顶点位移、层间最大位移角最大。

表3 顶点位移、层间最大位移角Table 3 Vertex maximum displacement the maximum displacement angle between layers
由表4转换层上下层的层间位移角分析可以看出:
二层层间位移角变化分析(θ2∶θ表示位移角,2表示模型。θ2表示第二个模型的位移角):
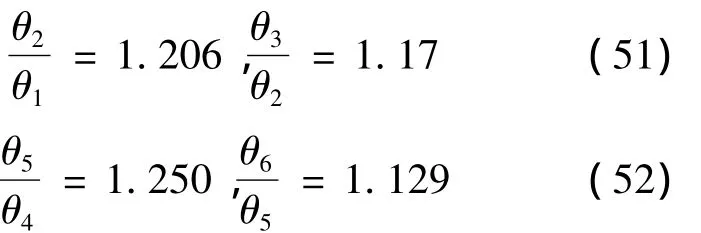
位移角增长率平均值:

由以上数据对比分析可得,一层转换层的层间位移角比上层小,但一层转换层的层间位移角基本保持不变。转换层上层结构的层间位移角随着剪力墙由边跨向中间布置的过程中逐渐增大,增长幅度较均匀。其位移角的平均增长率为 1.2。
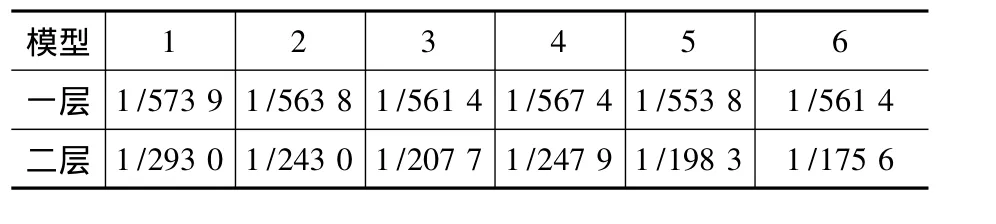
表4 层间位移角Table 4 Interlayer displacement angle
3.3 结构地震作用
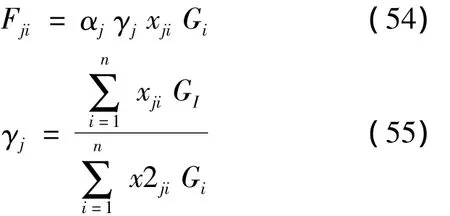
由于结构较高,除基本振型的影响外,高振型的影响较大,因此采用振型分解反映谱法考虑多个振型的组合。平面结构第j振型,i质点的等效水平地震力Fji为[4]:式中,αj相应于j振型自振周期Tj的地震影响系数,xji第j振型i质点的振幅系数;Gi为第 i层(i质点)重力荷载代表值,与底部剪力法中GE计算相同;γj是 j振型的振型参与系数[10]。
表5中列出了结构的基底剪力和基底弯矩。

表5 结构基底剪力和基底弯矩Table 5 Structure base shear and base moment

底部剪力比较:

底部弯矩比较:
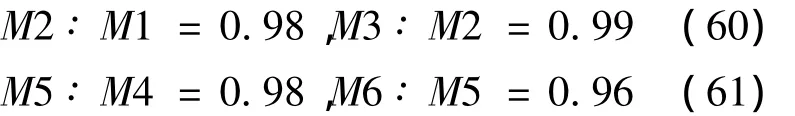
由上述数据对比分析可得,随着剪力墙由外围向中间布置过程中,结构的底部剪力和底部弯矩逐渐减小,且减小的幅度均匀。结构的底部最大剪力是最小剪力的1.32倍,最大弯矩是最小弯矩的1.18倍。由此说明结构上部剪力墙在周围布置底部剪力和弯矩较大,在中间布置底部剪力和弯矩较小。结构的刚度减小的同时其结构地震作用也相应的减小。
4 结论
综上所述,可以得到以下结论,供设计时参考:
(1)扭转刚度、侧向刚度和剪弯逐渐减小,侧向刚度、剪弯刚度减小幅度逐渐降低,扭转刚度的减小幅度逐渐增大。
(2)扭转周期和平动周期逐渐增大,平动周期增加幅度较均匀,扭转周期增加幅度逐渐增大。扭转周期跟平动周期比值的平均增长率是1.27,说明扭转周期比平动周期增大速率快,结构的扭转刚度比侧向刚度变化速率快。
(3)转换层上层结构的层间位移角逐渐增大,增长幅度较均匀。其位移角的平均增长率为1.2。
(4)结构的底部剪力和弯矩逐渐减小,减小幅度较均匀。结构的底部最大剪力是最小剪力的1.32倍,最大弯矩是最小弯矩的1.18倍。竖向构件布置位置引起刚度减小的同时,地震作用也相应减小。所以合理布置剪力墙的位置可以减小地震作用。
总之,随着剪力墙由周围向中间布置,结构的扭转刚度和侧向刚度逐渐减小,且扭转刚度比侧向刚度的减小速率快,结构的扭转周期和平动周期亦是如此。竖向构件布置位置引起刚度减小的同时,地震作用也相应减小,因此合理布置剪力墙的位置可以减小地震作用。
[1] 唐兴荣,何若全.高层建筑中转换层结构的现状和发展[J].苏州城建环保学院学报,2001,14(3):1-8.Tang Xingrong,He Ruoquan.Present situation and development of high-rise buildings conversion layer structure[J].Journal of Suzhou Institute of Urban Construction and Environmental Protection,2001,14(3):1-8.(in Chinese)
[2] 傅传国,鞠好学,宫志超.高层建筑托柱转换结构力学特点的分析与比较[J].山东建筑工程学院学报,2003,18(2):1-6.Fu Chuanguo,Ju Haoxue,Gong Zhichao.Analysis and comparison of high-rise buildings column transfer structure mechanical characteristics[J].Shandong Institute of Architectural Engineering,2003,18(2):1-6.(in Chinese)
[3] 王宾.框支剪力墙结构中剪力墙合理数量研究[D].合肥:合肥工业大学,2013.Wang Bin.The Research on reasonable number of shear wall in the frame effec of the munber of shear wall of frame aseismic behavior of shear wall structure supported supported sheav wall[D].Hefei:Hefei University of Technology,2013.(in Chinese)
[4] 黄勤勇,吕西林.转换层上、下刚度比对框支剪力墙结构抗震性能的影响[J].结构工程师,2003,(1):17-23.Huang Qinyong,Lu Xilin.The effect of stiffness ratio on conversion layer on the lower frame aseismic behavior of shear wall structure supported[J].Structural Engineer,2003,(1):17-23 .(in Chinese)
[5] 祁勇,朱慈勉.基于Push-over方法的框支短肢剪力墙转换层结构弹塑性分析[J].结构工程师,2010,(4):63-68.Qi Yong,Zhu Cimian.Elastoplastic conversion layer structure analysis based on frame supported push-over method of short shear wall[J].Structural Engineer,2010,(4):63-68.(in Chinese)
[6] 张叶田,吴云海.高层建筑转换层结构方案的选择[J].结构工程师.2009,(2):6-9+19.Zhang Yetian,Wu Yunhai.Choose high-rise building conversion layer structure programs[J].Structural engineer,2009,(2):6-9+19 .(in Chinese)
[7] 中华人民共和国住房和城乡建设部. JGJ3—2010高层建筑混凝土结构技术规程[S].北京:中国建筑工业出版社,2010.Ministry of Housing and Urban-Rural Development People's Republic of China .JGJ3—2010 Technical specification forconcrete structuresrise building[S].Beijing:China Building Industry Press,2010.(in Chinese)
[8] 中华人民共和国住房和城乡建设部. GB50011—2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.Ministry of Housing and Urban-Rural Development of the People's Republic of China.GB50011—2010 Code for seismic design of buildings[S].Beijing:China Building Industry Press,2010.(in Chinese)
[9] 赵兵.SATWE软件如何计算刚度比[J].建筑结构.2005,(12):79-82.Zhao Bing.SATWE software how to calculate the stiffness ratio[J].Building Structure,2005,(12):79-82.(in Chinese)
[10] 方鄂华,钱稼茹,叶列平.高层建筑结构设计[M].北京:中国建筑工业出版社,2005:145-146 Fang Ehua,Qian Jiaru,Ye Lieping.The structural design of high-rise building[M].Beijing:China Building Industry Press,2005:145-146.(in Chinese)

