匀强磁场与简谐势阱中的低维荷电自旋-1 玻色气体

李玉山

(菏泽学院物理系，菏泽274015)

1 引 言

玻色气体由于在一定的条件下能够展现出超导、超流、玻色–爱因斯坦凝聚(BEC)等奇特现象而成为凝聚态物理研究的热点之一. 在各种类型的势阱及外场约束下，玻色气体所表现出的相变特征和磁学性质更是人们关注的重点. 前人的研究大多集中于单纯势阱约束的玻色气体［1-3］、磁场中的荷电自旋-1 玻色气体［4，5］、磁场和势阱中不考虑自旋-磁场作用的玻色气体［6-8］等方面，关于自旋-磁场作用究竟会如何影响磁场和势阱中玻色系统的相变和磁性质的研究很少见到报道. 电荷自由度和自旋自由度都将会对磁场和势阱中的荷电玻色气体相变和磁性产生重要影响，电荷自由度将导致朗道抗磁性，自旋自由度则会引起泡利顺磁性，两种作用的相互竞争下系统将会呈现怎样的性质是我们本文关注的重点.

近年来，人们对超导体层状结构及磁性薄膜材料的关注，激发了人们对于低维玻色系统的兴趣，因此研究低维系统对于开发新材料和器件也有着重要的物理意义［9-13］. 本文选取的研究模型为匀强磁场和简谐势阱约束的二维自旋-1 理想荷电玻色气体，研究的重点为电荷-磁场和自旋-磁场作用的竞争对BEC 相变和磁性质的影响.研究方法为截断求和法和半经典近似相结合，并将所得结果与磁场和简谐势阱中不考虑自旋-磁场作用的玻色系统进行比较.

2 物理模型及解析推导

将质量为m，电量为q，自旋为1 的理想玻色系统，置于各向同性简谐势阱和z 轴方向的匀强磁场中. 该模型所对应的单粒子哈密顿和能谱可表示为

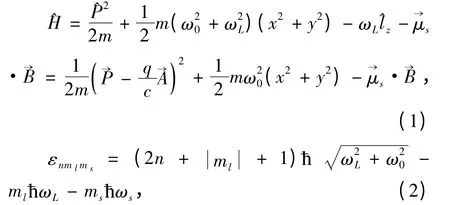
式中，ω0和ωL分别代表势阱频率和Larmor 频率，ωs= μsB/ħ 为自旋引起的角频率.·为内禀磁矩=(mc)与外磁场→B 的相互作用能，→S为自旋算符. ^lz是角动量在z 轴方向的投影，→A 是磁场→B 对应的矢量势. 量子数n = 0，1，2，...;ml= 0，±1，±2，... ;ms= -1，0，1.

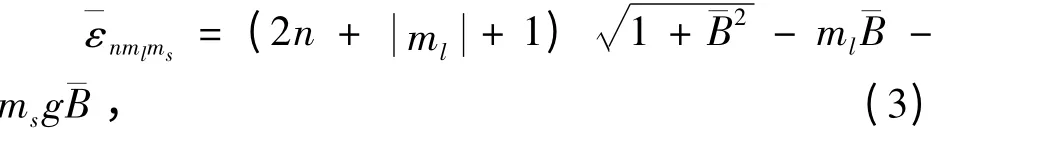
当系统热能量远大于能级间隔时，也可采用半经典近似研究该模型，将分立能谱看成连续谱，对量子数的求和用对量子数的连续积分来代替，此时激发态粒子数可化简为

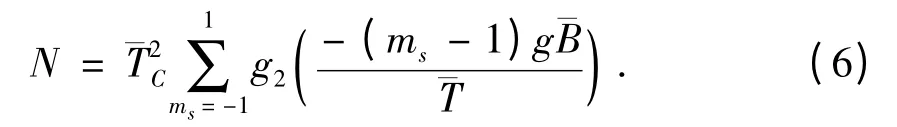
临界温度之下，凝聚在基态的粒子所占的比例为

代表玻色分布函数. 半经典近似下，

3 结果及讨论

首先对截断近似法做可靠性分析，进而给出求和量子数取何值时，截断项数能够达到系统要求. 为计算和表述方便，用nmax来统一代替式(4)和(8)中的求和量子数n 和ml的最大值，即定义n ∈［0，nmax］，ml∈［- nmax，nmax］. 假定系统的总粒子数N 为1000，图1 给出了BEC 临界温度随nmax倒数的变化. 当1/nmax≤0.005 ，即nmax≥200 时，开始收敛，g 越大，需要更大的nmax才能收敛. 为保证计算结果可靠，本文以下的计算选定nmax= 1000 ，并引入符号TSA 和SCA 分别表示截断求和法和半经典近似结果.

图4 给出了基态粒子凝聚比例随温度的变化关系，相同磁场不同自旋g 因子的粒子遵循了基本相同的规律，由插图可以看出，这种变化规律也不因磁场的不同而发生较大的改变.

图7 给出的自旋g 因子临界值gc随温度和磁场的变化表明半经典近似依然不可靠. 截断近似结果表明，固定温度下，gc随磁场增大而增大，弱磁场区域，gc随磁场变化比较剧烈，随着磁场的增强，增加的趋势变缓慢，最终趋于固定值.固定磁场下，gc随温度升高而缓慢下降，但下降的趋势非常小.

图1 BEC 临界温度 随1/nmax 的变化( = 0.5 ，N = 1000 )Fig.1 The BEC critical temperature versus the inverse truncated order for = 0.5 and N = 1000

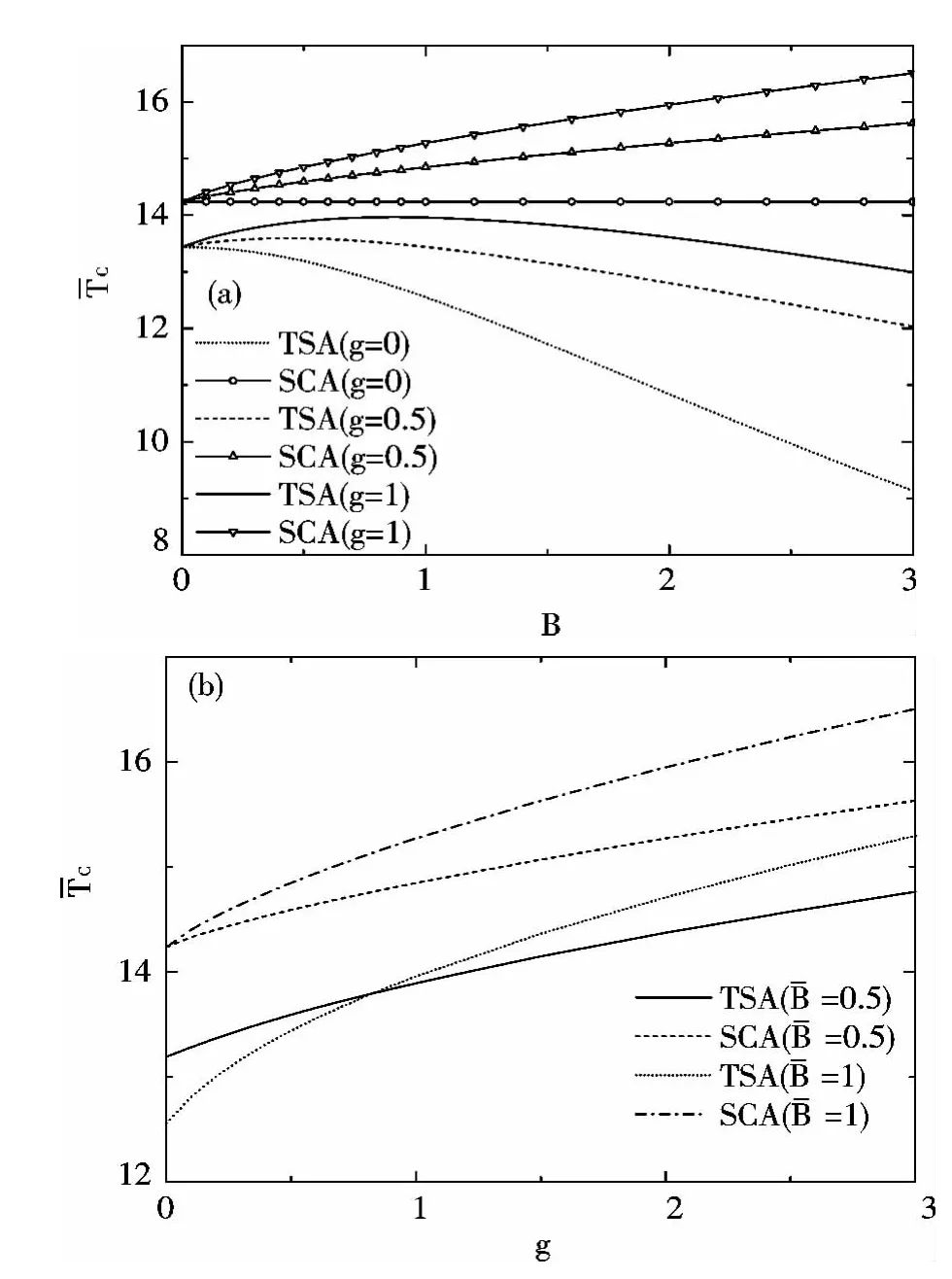
图2 随(a)磁场 和(b)自旋g 因子的变化规律Fig.2 Plots are the BEC critical temperature as a function of (a)magnetic field and (b)spin g-factor

图3 随粒子数N 的变化(= 0.5 )Fig.3 The BEC critical temperature versus the number of particles for= 0.5

图4 基态粒子凝聚比例随温度的变化，横轴约化温度为各自的BEC 临界温度. 插图为不同磁场时的TSA 值Fig.4 Condensate fraction of ground states versus the temperature. The temperature is scaled by their respective BEC critical temperature. Inset:TSA results for different magnetic field

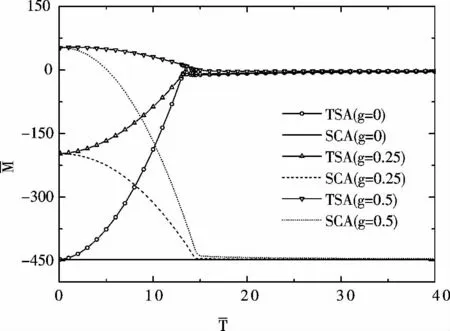
图5 磁场 = 0.5 时，磁化强度随温度的变化Fig.5 The magnetization versus temperature for magnetic field = 0.5

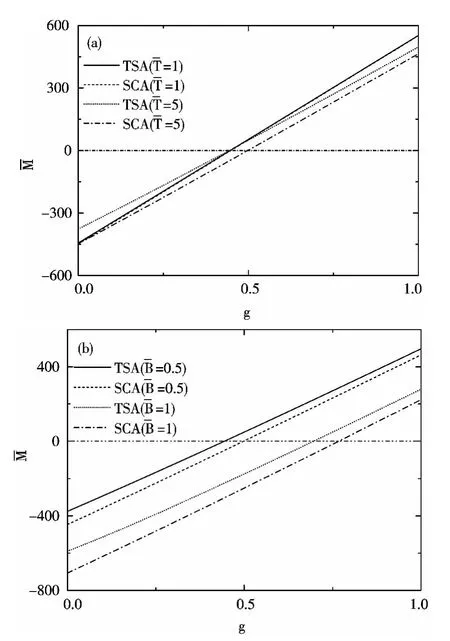
图6 磁化强度 随自旋g 因子的变化:(a)固定磁场 = 0.5 ，(b)固定温度 = 5Fig.6 The magnetization versus the spin g-factor for (a)fixed magnetic field =0.5 and (b)fixed temperature = 5

图7 自旋因子临界值gc 随(a)磁场和(b)温度的变化Fig.7 The critical value of spin factor gc versus (a)magnetic field and (b)temperature

4 结 论

通过对磁场和势阱中二维自旋-1 理想荷电玻色气体的研究，给出低维玻色系统的相变特征和磁性质. 自旋-磁场作用能够增强BEC 临界温度，而电荷-磁场作用会降低BEC 临界温度，二者的竞争将导致BEC 临界温度随磁场先略微上升后缓慢下降. 自旋效应并不明显改变BEC 临界温度随粒子数的变化及基态粒子凝聚随温度的变化.引入自旋g 因子来描述系统的顺磁性效应，随着g 的增加，磁化强度呈现抗磁性到顺磁性的转变.gc受温度影响较小，但随外磁场的增大而增大，最终趋于某一固定值.

［1］ Bagnato V，Prichard D E，Kleppner D. Bose - Einstein condensation in an external potential［J］. Phys.Rev. A，1987，35:4354.

［2］ Bagnato V，Kleppner D. Bose-Einstein condensation in low-dimensional traps［J］. Phys. Rev. A，1991，44:7439.

［3］ Yan Z. Bose -Einstein condensation of a trapped gas in n dimensions ［J］. Phys. Rev. A，1999，59:4657.

［4］ Jian X L，Qin J H，Gu Q. Diamagnetism versus paramagnetism in charged spin - 1 Bose gases ［J］. J.Phys.:Condens. Matter，2011，23:026003.

［5］ Qin J H，Jian X L，Gu Q. Magnetic properties of charged - 1 Bose gases with ferromagnetic coupling［J］. J. Phys.: Condens. Matter，2012，24:366007.

［6］ EI-Badry A M. Temperature dependence for the synthetic magnetization of a rotating Bose gas in harmonic trap［J］. Turk. J. Phys.，2013，37:30.

［7］ Fan J H，Gu Q，Guo W. Thermodynamics of charged ideal Bose gases in a trap under a magnetic field［J］.Chin. Phys. Lett.，2011，28:060306.

［8］ Li Y S. Numerical method to charged Bose gases under harmonic trap and magnetic field ［J］. J. At. Mol.Phys.，2014，31(5):821 (in Chinese)［李玉山.Numerical method to charged Bose gases under harmonic trap and magnetic field［J］. 原子与分子物理学报，2014，31(5):821］

［9］ Bayindir M，Tanatar B. Bose -Einstein condensation in a two-dimensional，trapped，interacting gas［J］.Phys. Rev. A，1998，58:3134.

［10］ van Zyl B P，Hutchinson D A W. Charged two -dimensional quantum gas in a uniform magnetic field at finite temperature ［J］. Phys. Rev. B，2004，69:024520.

［11］ Patrick S，Brandon P v Z. Thermodynamic properties of a harmonically trapped，two - dimensional charged quantum gas in a magnetic field ［J］. J. Phys. A:Mathematical and Theoretical，2008，41:135305.

［12］ Tung S，Lamporesi G，Lobser D，et al. Observation of the presuperfluid regime in a two - dimensional Bose gas［J］. Phys. Rev. Lett.，2010，105:230408.

［13］ Merloti K，Dubessy R，Longchambon L，et al. A two-dimensional quantum gas in a magnetic trap ［J］.New J. Phys.，2013，15:033007.