外压下VN 相变和力学性质的第一性原理研究
谭 心,穆庆鸽,王洋洋,刘学杰
(1. 东北大学机械工程与自动化学院,沈阳110000;2. 内蒙古科技大学机械工程学院,包头014010)
1 引 言
过渡金属氮化物具有高硬度、高熔点、耐磨和抗腐蚀,以及高温化学稳定性和良好的导电导热性,因而广泛地应用于耐高温、耐磨损领域.20 世纪80 年代末,Helmerson 等人[1]首次报道在超晶格TiN/VN 薄膜中发现超硬效应,由此进入了对VN 的研究热潮. VN 的热、化学稳定性非常高,机械性能强且具有极高的硬度,被广泛用做耐磨材料和切削工具. 由于VN 作为刀具涂层在工作过程中瞬时可能承受很大的应力,因此十分有必要探索压力对VN 的相对稳定性和力学性能的影响.
1992 年B Palanivel 和M Rajagopalan 等人运用TB-LMTO 预测VN 在压力达到65.2 GPa 时将发生从NaCl 型到CsCl 型的结构转变[2]. 2006 年Poonam 等人利用离子间相互作用势模型计算了高压下TiN、MoN、VN、NbN、HfN、ZrN 等过渡金属氮化物的结构相变,通过得到的相对体积随压力变化曲线预测VN 由NaCl 型到CsCl 型的相变压力为102GPa,NbN 由NaCl 结构到CsCl 结构的相变压力为127 GPa[3]. 2007 年,E. I. Isaev 等人对过渡金属碳化物及其氮化物的声子相关性质进行了第一性原理的研究,发现NaCl 结构的第五副族氮化物的声子谱有异常特征,V 族过渡金属氮化物的声子谱沿着高对称点X 方向存在明显的虚频,不符合B1 结构(NaCl 型)的VN、NbN、TaN 的动态稳定特性[4]. 2012 年Asvini Meenaatci等人运用第一性原理使用vasp 软件包计算了第五副族过渡金属氮化物的电子结构、结构稳定性、力学和超导特性,得到VN 由NaCl 结构到CsCl结构的相变压力为272GPa,并且首次研究了其由WC 结构到NaCl 结构的相变得到相变压力为28.5 GPa[5].
目前,常压下VN 的稳定结构究竟是Bh 型还是B1 型仍存有异议,同时对于VN 相变的研究得出的结论各不相同,得到的相变点差别较大,且缺乏对压力下力学性质的研究. 综上,本文采用赝势平面波方法,从焓压关系、力学稳定性、声子色散关系等层面,分别对不同压力下B1、B2、Bh 三种构型的VN 进行计算,并进一步对VN 在高压下的结构稳定性和力学性质等进行深入探讨.
2 计算方法
本文采用基于密度泛函理论的第一性原理方法,运用VASP 软件包对外压下VN 的结构和性能进行了计算. 计算采用平面缀加波(PAW)和广义梯度近似(GGA)的交换关联势PW91. 结构优化的平面波截断能取为450 eV (B1 结构和B2结构)和400 eV (Bh 结构),k 点的网格密度为13 ×13 ×13 (B1 结构)、17 ×17 ×17 (B2 结构)和11 ×11 ×9 (Bh 结构).
计算焓压关系曲线时使用了QUANTM ESPRESSO 软件包(PWscf),利用其中的ev. x 模块. 对于立方晶系输入文件按照晶格常数-能量给出,而对于Bh 结构所属的六方晶系输入文件是按照体积-能量给出. 通过PwScf 进行物态方程拟合从而得出压力与晶格常数、焓等的关系,该方程可表示为:

式中E0和V0分别表示常压下每个VN 单胞的总能E 和体积V,B0为常压下的体弹模量,B' 为体弹模量对压力的一阶导数.
弹性常数描述了晶体对外加应变的响应刚度,B1、B2 结构的VN 所属的立方晶系独立弹性劲度常量为C11,C12,C44. 采用Voigt-Reuss-Hill 近似可得到立方晶系体模量和剪切模量的计算公式[6]:
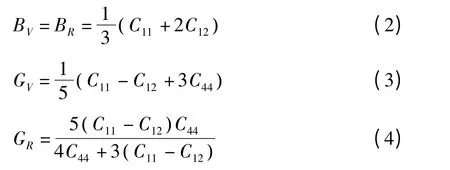
Bh 结构的VN 属于六角晶系独立弹性劲度常量为C11,C12,C13,C33,C44. 六方晶系体模量和剪切模量的计算公式[7]:
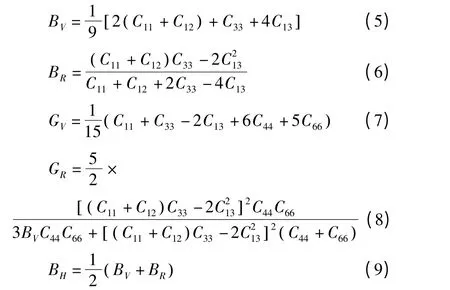

多晶体下各材料的杨氏模量和泊松比计算公式为:

计算声子谱时使用了Phonopy +VASP,其基本方法是构造超原胞,把原子移动一下,计算原胞中所有原子所受的力,然后根据这个力构造力常数矩阵,得到声子谱. 计算实空间的力常数时选取的平面波截断能为500 eV,选用2 ×2 ×2 的超胞,电子和离子迭代次数使用的能量差收敛标准为10-8eV.
3 结果与讨论
3.1 结构稳定性
计算常压下VN 的三种构型平衡态的晶格常数,如表1 所示. 通过与前人理论值及实验值对比,误差基本都在5%以内,结果与他人计算和实验值吻合得非常好.
对于三种结构的VN,在其平衡态晶格常数附近取一些不同的晶格常数点,然后根据Quantum ESPRESSO 软件包(Pwscf)得到的总能及体积,把它们代入Murnaghan 状态方程,进而得到体积能量曲线,如图1 所示.
B1 结构VN 的体积-能量曲线分别与Bh 结构和B2 结构的VN 体积-能量曲线之间存在公切线,求得切线斜率后就可以得到不同相之间的相变压力[16],相变压力可以由下式得到:

用这种方法所求得的两条公切线的斜率分别为-0.9379,-0.1892,然后用斜率的绝对值乘以160.2 即可得到相变压力,所得相变压力分别为150.2GPa 和30.3GPa. 相变压力还可以通过计算Gibbs 自由能G=E0+PV +TS 得到,在一定的温度和压力下的最稳定结构,其吉布斯自由能应该是最小的,由Murnaghan 状态方程可以得到体积V 与压强P 的关系然后通过公式G =E0+PV +TS ( T=0K )(此时吉布斯自由能为G =E0+PV 与焓H=E0+PV 相等),可以得出:

表1 常压下VN 平衡态的晶格常数Table 1 The lattice constants of equilibrium VN at ambient pressure
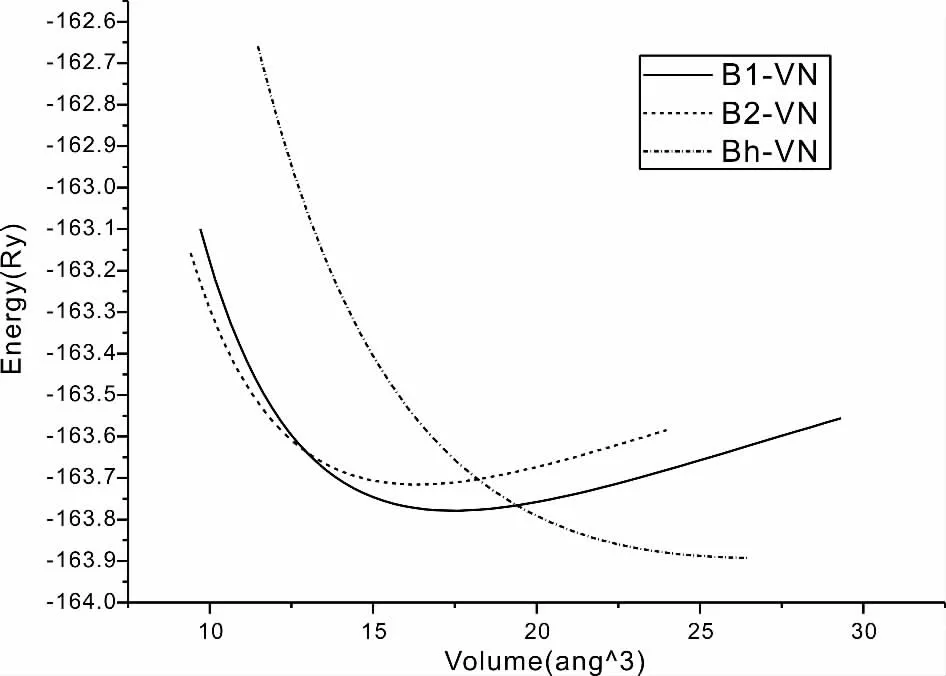
图1 Bh、B1 和B2 结构VN 的能量与体积关系曲线Fig.1 Energy as function of volume for Bh,B1 and B2 VN

图2 B1,B2,Bh 结构VN 焓与压力关系曲线Fig.2 Enthaply as function of pressure for Bh,B1 and B2 VN

据此得出Gibbs 自由能和压力的关系曲线,亦即焓与压力的关系曲线.相平衡的判定需要满足两个条件:①两相的压力相等②两相的吉布斯自由能相等,在T =0K 时,也就是两相的焓值相等,关系式表示如式(13)所示[17]:

图中Bh-VN 和B1 -VN 曲线的交点,即为Bh 结构到B1 结构的相变点为31.02 GPa,而B1-VN 和B2 -VN 的曲线的交点即相变点为149.2 GPa,表2 给出了VN 的相变压力及与他人的对比. 两种方法计算的相变压力基本相等. 因此我们推测Bh 结构到B1 结构的相变点在30 GPa 左右,B1 结构到B2 结构的相变点在150 GPa 左右.

表2 VN 的相变压力Table 2 Calculated transition pressure for VN
3.2 高压下弹性性质的研究
三种结构VN 在不同压力下的弹性常数(Cij)、体弹模量(B)、剪切模量(G)、杨氏模量(E)、B/G、泊松比和弹性各向异性因子A 如表3、表4、表5 所示.

表3 压力下Bh 结构VN 的力学常数Table 3 The mechanical constants of Bh VN under the pressure
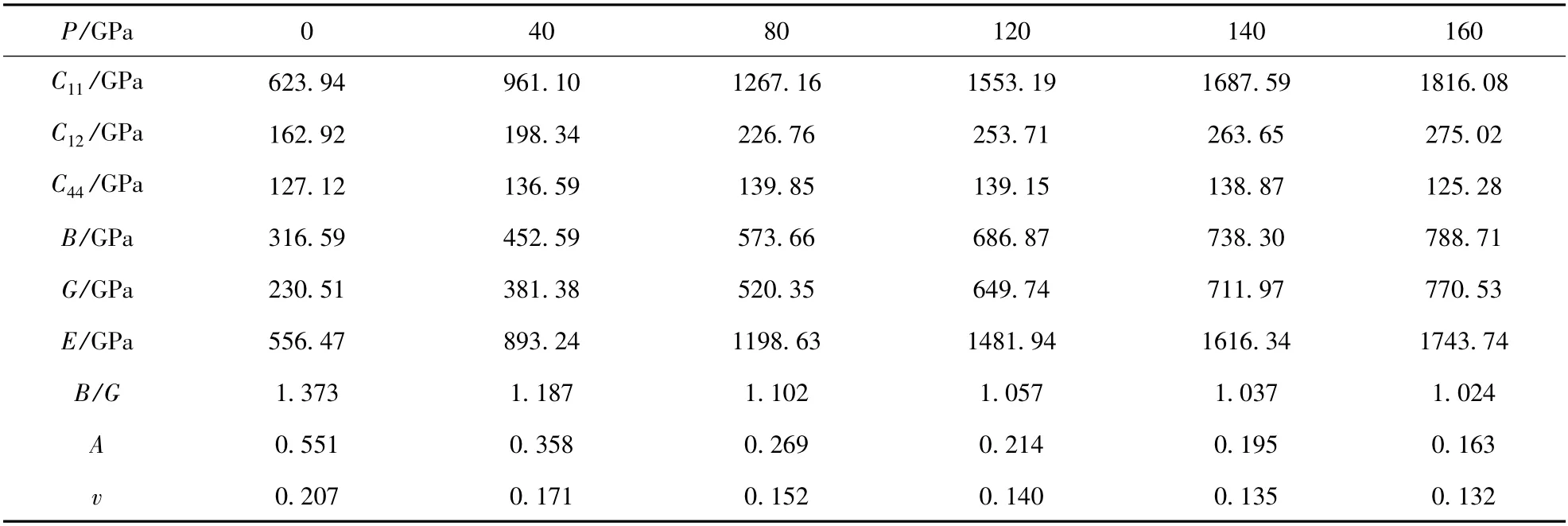
表4 压力下B1 结构VN 的力学常数Table 4 The mechanical consants of B1 VN under the pressure

表5 压力下B2 结构VN 的力学常数Table 5 The mechanical consants of B2 VN under the pressure

由图3 可以看出,Bh 结构随压力的增加各弹性常数线性增加,超过30 GPa 后C12的值高于C66. 在相变点之前B1 结构的C44随压力增大而增大,B2 结构的C44随压力的增加而增大,两种结构的C11和C12随压力的增加呈线性增加. 与C12相比C11随压力的变化幅度更大,体模量B 随压力增大而逐渐变大,说明其越来越难以被压缩.

采用式(14)绘制杨氏模量的三维各向异性图

式中l1,l2,l3分别表示在矢量与正交坐标轴之间的夹角余弦,在球坐标下可表示为:l1=sinθcosφ,l2=sinθsinφ ,l3=cosθ . 采用Mathematica 软件即可绘制出球坐标下杨氏模量三维各向异性图.
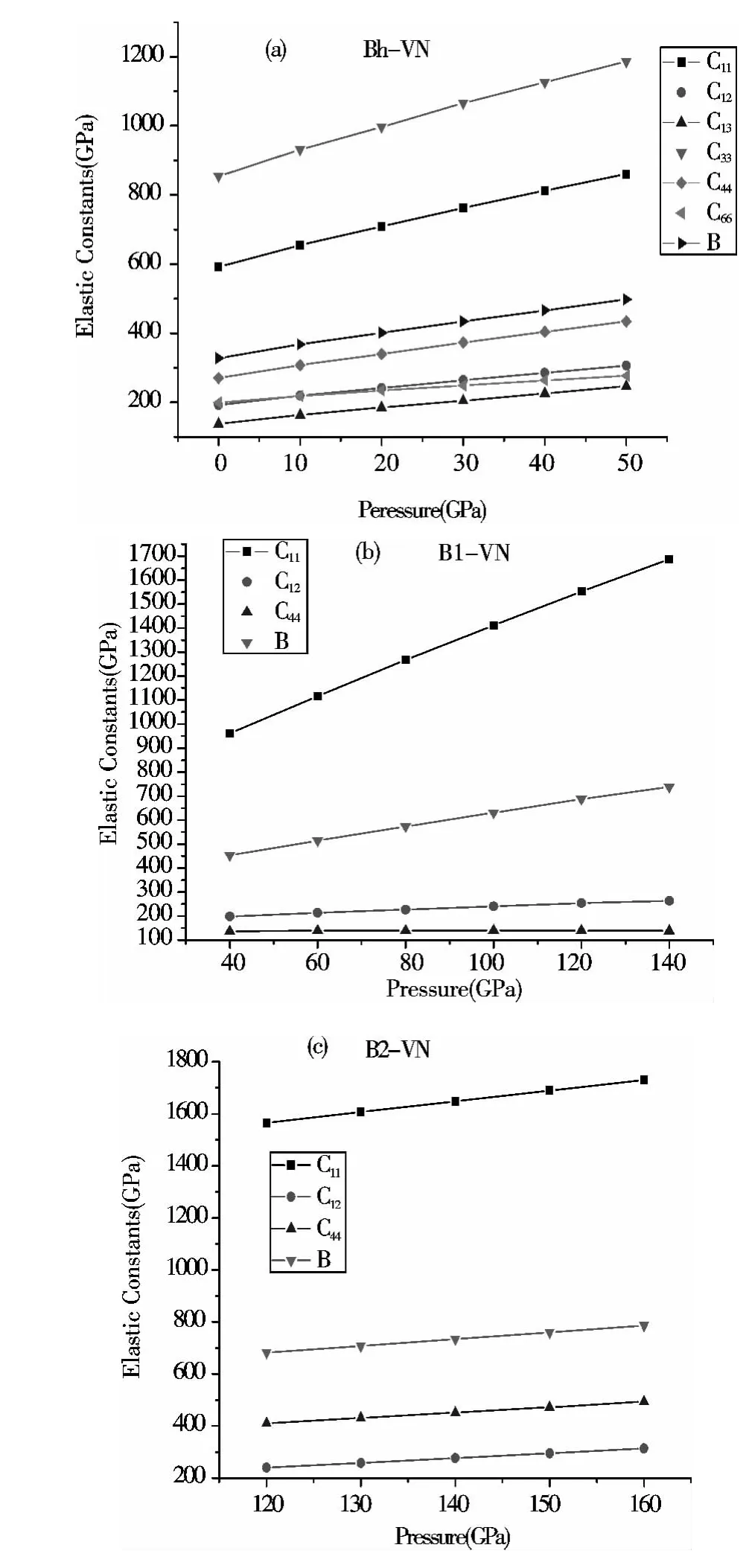
图3 三种构型的VN 随压力变化的弹性常数和体模量Fig.3 The elastic constants as a function of pressure of the three types of VN
对于各向同性体系,其杨氏模量三维图是一个球形,图4 (a)— (e)分别表示了0 GPa、140 GPa 下B1 和B2 结构的VN 杨氏模量三维图及其投影图. 由图4 可以看出两种构型的VN 的曲面图与球面都有很大的偏差,因此都表现出了较强的各向异性,这与表4 和表5 的A 值表现出的性质一致,随压力的增加B1 -VN 的A 值逐渐减小而B2 -VN 的A 值是增大的,表明压力增加B1 结构的各向异性程度增加而B2 结构各向异性程度减小. 特别是对于B1 结构,从图4 可以看出坐标基矢方向的值比体对角线方向的值大,明显大很多,因此随压力的增加B1 结构的各向异性程度显著增加,同时也说明晶格畸变以及裂纹在[111]方向出现的概率最大. 而对于B2 结构坐标基矢方向的值与体对角线方向上的值差距与B1结构相比明显小很多,其各向异性程度随压力增加而减小.

图4 不同压力下B1 -VN 和B2 -VN 的杨氏模量三维各向异性曲面图及其在XY 平面的投影图Fig.4 Anisotropic properties of Young modulus and their projections on the XY plane under different pressures for B1 -VN and B2 -VN
3.3 声子色散关系的研究
通过VASP +Phonopy 计算三种结构VN 的声子色散关系如图5、图6 所示.
图6a 中Bh-VN 声子谱在整个布里渊区并没有出现虚频,因此基本上可以认为Bh 结构在零压下是动力学稳定的. 图6b 表明零压下B2 -VN声子谱沿高对称点M 方向有较大的虚频,动力学不稳定. 从图5、6(b)可知,零压下B1 与B2 结构的VN 不稳定,是因为丧失了动力学稳定性.通过对三种构型零压下的声子谱研究表明,六角WC 结构比立方结构更稳定.
随着压力增大,B2 -VN 声子谱的虚频减弱,当达到140 Gpa 时,在整个布里渊区不存在虚频,如图6c 所示,说明其满足振动方面的稳定性条件,这与之前焓压关系曲线得出的结论基本相同.
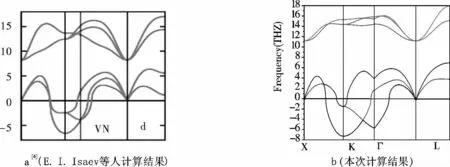
图5 零压下B1 -VN 的声子谱Fig.5 The phonon spectra for B1 -VN at ambient pressure

图6 B2 和Bh 结构VN 的声子谱Fig.6 The phonon spectra for B2 and Bh-VN
4 结 论
利用基于密度泛函的第一性原理方法,使用VASP 及Quantum ESPRESSO (PWscf)软件包,对B1、B2、Bh 三种构型的VN 进行了结构优化,计算了不同体积下体系的总能量、一定压力下体系的焓,以及三种构型的VN 在高压下的力学性质,使用Phonopy 软件包计算了声子色散关系.通过这三方面的研究推测,VN 由Bh 到B1 结构,B1 到B2 结构的相变点分别为30 GPa 左右和150 GPa 左右. 焓压曲线及声子色散关系表明,零压下六角结构的VN 较立方结构的B1、B2 型更稳定. 力学稳定性方面判定,在达到140 GPa 时B1结构的VN 会失稳,这也与计算得到的相变点压力基本一致. 但是通过力学判据还未能确定Bh结构到B1 结构的相变,还需要进一步研究验证.随着压强的增大弹性常数、弹性常量基本上都是呈增大趋势,总体来看随压力的增大晶体被压缩,同时使其抵抗变形的能力增强. 三种构型的VN都属于脆性材料. VN 的弹性各向异性特征明显,随压力的增大,B1 结构的各向异性程度显著增加,B2 结构的各向异性程度减小.
[1] Helmersson U,et al. Growth of single -crystal TiN/VN strained - layer superlattices with extremely high mechanical hardness [J]. Appl. Phys.,1987,62(2):481.
[2] Palanivel B,Rajagopalan M. The high-pressure phase transition and superconductivity of VN studied by the LMTO method[J]. J. Phys.:Condens. Matter,1992,4:10377.
[3] Poonam O,Mahendra A,Sankar P S. Pressure -induced structureral phase transformation and elastic properties of transition metal mononitrides[J]. Journal of Physics and Chemistry of Solids,2007,68:148.
[4] Isaev E I,Simak S I,Abrikosov I A,et al. Phonon related properties of transition metals,their carbides,and ni-trides:A first-principles study[J]. Journal of Applied Physics,2007,101:123519.
[5] Meenaatci A A T,Rajeswarapalanichamy R,et al. Electronic structure,structural stability,mechanical and superconducting properties of group VB nitrides:A first principles study[J]. Solid State Sciences,2013,19:36.
[6] Ding Y C,Xiao B. Electronic structure,mechanical properties and intrinsic hardnessfa new superhard material BeP2N4[J]. Acta Phys. Chim. Sin.,2011,27(7):1621(in Chinese)[丁迎春,肖冰. 一种超硬新材料BeP2N4的电子结构和力学性质及本征硬度[J]. 物理化学学报,2011,27(7):1621]
[7] Yao Q,Xing H,et al. Theoretical calculation of elastic properties of TiB2and TiB[J]. The Chinese Journal of Nonferrous Metals,2007,17(8):1297.
[8] Ivashchenko V I,Turchi P E A,Shevchenko V I,et al. First - principles study of phase stability of stoichiometric vanadium nitrides [J]. Phys. Rev. B,2011,84:174108.
[9] Stampfl C,Mannstadt W,Asahi R,et al. Electronic structure and physical properties of early transition metal mononitrides:Density -functional theory LDA,GGA,and screened-exchange LDA FLAPW calculations[J]. Phys. Rev. B,2001,63:155106.
[10] Papaconstantopoulos D A,Pickett W E,Klein B M,et al. Electronic properties of transition -metal nitrides:The group - V and group - VI nitrides VN,NbN,TaN,CrN,MoN,and WN [J]. Phys. Rev. B,1985,31:752.
[11] Shimizu H,Shirai M,Suzuki N. Electronic,structural and magnetic properties of transition - metal mononitrides[J]. Journal of the Physical Society of Japan,1997,66:3147.
[12] Zhukov V P,Gubanov V A,Jepsen O,et al. Calculated energy-band structures and chemical bonding in titanium and vana-dium carbides,nitrides and oxides[J]. J.Phys. Chem. Solids,1988,49:841.
[13] Zhao B R,Chen L,Luc H L. Supercorducting and normal-state properties of Vanadium nitride[J]. Phys.Rev. B,1984,29:6198.
[14] Pearson W B(Ed). Structure reports for 1967[M]. A.Oosthoek's Utgeversm-aatschappij NV,1974.
[15] Chinnappan R. First - principles study of ground -state properties and phase stability of vanadium nitrides[J]. CALPHAD:Computer Coupling of Phase Diagrams Thermochem.,2009,33:469.
[16] Jaffe J E,Hess A C. Hartree -Fock study of phase changes in ZnO at high pressure[J]. Phys. Rev. B,1993,48:7903.
[17] Li Y Q. First principle studies on the structures and properties of TiN and Ti-Si-N under pressures[D].Inner Mongolia University of Science and Technology,2012:30 (in Chinese)[李瑜庆. 外压下TiN、Ti-Si-N 结构和性能的第一性原理研究[D]. 内蒙古科技大学,2012:30]
[18] Zener Clarence M. Elasticity and anelasticity of metals[M]. Chicago:University of Chicago Press,1948:76.

