刃型位错形成对面心立方金属Cu 体积的影响

何 坤，韩 明

(1. 山东理工大学机械工程学院，淄博255049;2. 福建工程学院材料科学与工程学院，福州350108)

1 引 言

位错是晶体中普遍存在而又十分重要的一类线缺陷. 晶体中的位错有刃型位错和螺型位错两种基本类型，其中形成螺型位错不会引起晶体体积的变化［1］，然而目前的研究报道并没有明确指出刃型位错形成后晶体体积的变化情况，因此有必要对该问题进行研究.

Huang［2］等利用透射电镜原位观察单晶SnO2纳米线电极的锂化过程，发现随着锂化时间加长，纳米线体积最终膨胀到240%左右，同时观察到该过程伴随着位错的大量增殖. Garcia -Mateo［3］等通过高分辨膨胀测定法估算无碳贝氏体位错密度，指出贝氏体转变时晶体体积的膨胀不是来自于母相奥氏体切变产生的弹性形变，而是由位错大量增殖产生的塑性变形造成的. Goland［4］以及Jens［5］等通过理论计算的方法对位错产生与晶体体积变化进行了研究.

本文采用分子动力学方法，使用EAM 势，模拟面心立方金属Cu 单晶的刃型位错，根据能量最低原理［6］，计算了刃型位错形成对晶体体积的影响.

2 模拟方法

使用 Large-scale atomic/Molecular Massively parallel Simulator (Lammps)软件，Foil［7］的势函数，在0K 条件下模拟Cu 单晶的刃型位错，模拟过程中时间步长为5 × 10-4ps，采用微正则系综(NVE).

模型采用正交平行六面体盒子，如图1 所示，X，Y 和Z 方向依次是［11 2］，［110］和［111］方向，其中Y 方向采用非周期边界，X 和Z 方向采用周期性边界. 模型在三个方向的长度分别为Lx=12.5445 Å，Ly=256.8972 Å，Lz=561.4356 Å，其中Y 方向凸台为两层原子面，凸台在Z 方向高h=325.5909 Å，晶格参数a =3.6150 Å，整个模型包含162942 个原子. 模型分为5 个组，除II 组原子设定为自由外，其余四组原子均固定，将IV 组沿图中Y 轴负方向推进一个单位柏氏矢量，II 组中就产生了刃型位错.

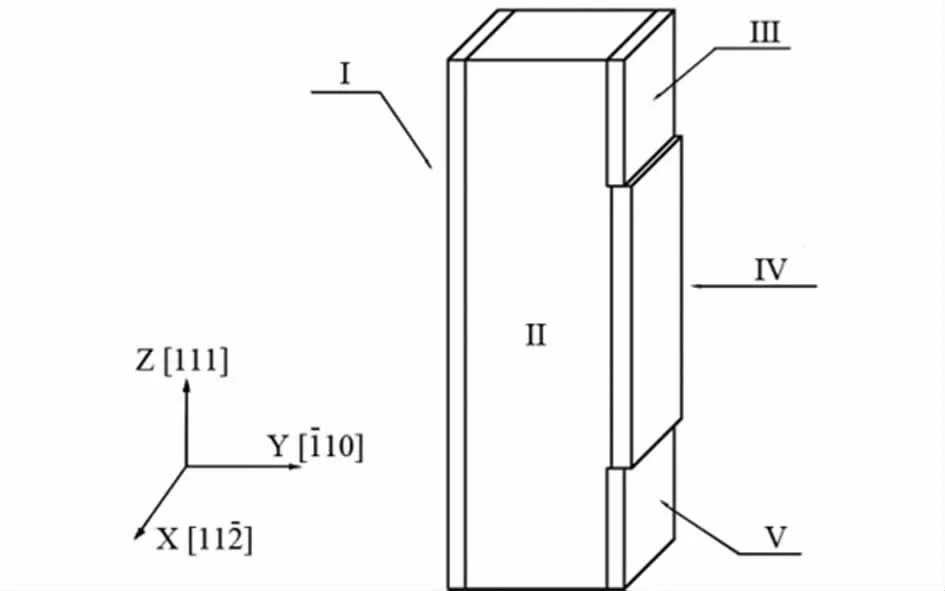
图1 模拟模型，I ～V 为模型分组编号Fig. 1 Simulation model，I ～V are the model sequence number

3 结果与分析

经充分弛豫，刃型位错产生后的原子组态如图2 所示，由图可以看出刃型位错两个多余半原子面发生分离，两半原子面间的原子产生错排，由相对于近邻层的正三角位置移动至倒三角位置，目前有研究认为该组态为扩展位错［8，9］，然而面心立方金属中的刃型位错组态是否如Hull［10］等描述的情况——两多余半原子面相邻排列，仍未得到证实. 图3 为刃型位错滑移面附近原子势能值，图中的两个能峰对应于两个多余半原子面，在远离能峰的边界处出现了能量异常区域，如图3 中圆圈所示，由于实际晶体中形成位错时，所有原子都可以自由弛豫，原子能量从产生位错的畸变区到晶体的理想排列区是一个渐变的过程，不会发生能量突变，因此这是不合理的现象，结合前人研究成果推知，产生该现象的原因是推入产生刃型位错的同时导致晶体体积减小［11］.

基于上述实验现象，利用模拟软件通过控制I 组的移动来消除这一变化，并由此得到I 组的位移量与整个模型原子平均能量关系曲线，如图4所示，图中横坐标代表I 组位移量，其正方向表

图2 刃型位错原子组态，黑色和灰色小球分别代表滑移面上方以及下方原子Fig. 2 Atomic configuration of edge dislocation，the black and grey globules represent the atoms above and below the slip plane，respectively

示I 组移动方向与刃型位错产生方向相同，负方向则相反，纵坐标代表整个模型的原子平均能量，由图可知，I 组位移量与模型原子平均能量呈抛物线关系，当I 组位移量为某一特定值时系统总能量最低，以该位置为标准，增加或减少I 组位移量，都将导致模型能量增加，根据能量最低原理，得出该位移量对应的晶体状态即为产生 平衡态刃型位错的状态，此时刃型位错附近滑移面原子能量如图5 所示，由图可知，在刃型位错达到平衡状态时，滑移面的能量突变消除，能量分布合理化.

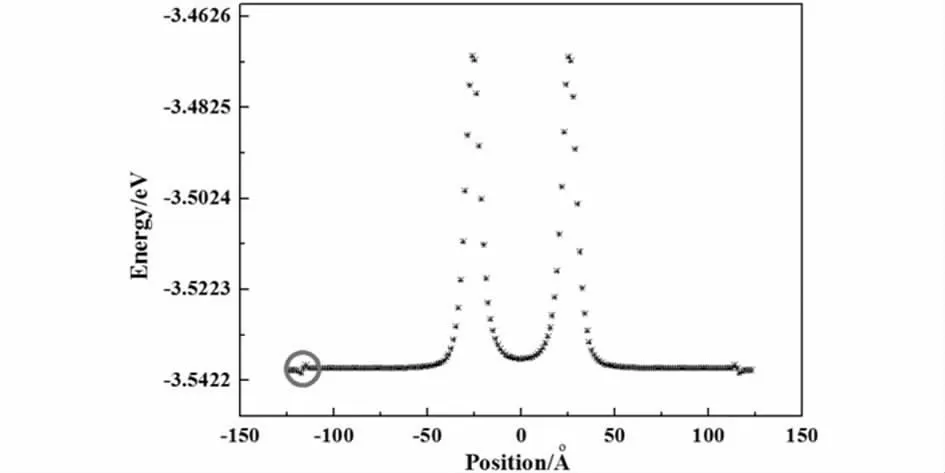
图3 滑移面附近刃型位错原子势能值Fig. 3 Atomic potential energy of the edge dislocation around slip plane

为了确定产生平衡态刃型位错后晶体体积变化情况，同时计算了初始模拟模型的原子密度，得到p理想=0.08467 (个/Å3)，该结果与面心立方单胞计算出来的原子密度一致，通过对比发现，刃型位错达到平衡状态时，p位错＜p理想，原子密度减小，晶体体积变大.

图4 I 组位移量与模型原子平均能量Fig. 4 The displacement value of part I and atomic average potential energy of the model

图5 滑移面附近稳态刃型位错原子势能值Fig. 5 Potential energy of the equilibrium edge dislocation around slip plane

进一步考察刃型位错产生方法对实验结果的影响，在初始模型基础上将III 组与V 组沿模型Y轴正方向抽出一个单位柏氏矢量形成刃型位错，用同样方法处理实验结果，最终得到抽出方法产生的平衡态刃型位错原子密度p'位错=0. 08465(个/Å3)，这一结果与用推入方法产生的平衡态刃型位错原子密度一致，即p位错= p'位错，由此得出，不管通过哪种方法获得刃型位错，晶体体积膨胀量一样.

4 结 论

本文使用分子动力学方法模拟了面心立方金属Cu 单晶的刃型位错，计算了刃型位错产生后金属体积的变化，得出以下结论:面心立方金属Cu 单晶产生刃型位错后晶体体积增大.

［1］ Wang Y N，Chen S J，Dong X C. The theory and application of Dislocation ［M］. Beijing:Metallurgical Industry Press，2007 (in Chinese)［王亚男，陈树江，董希淳. 位错理论及应用［M］. 北京:冶金工业出版社，2007］

［2］ Huang J Y，Zhong L，Wang C M，et al. In situ observation of the electrochemical lithiation of a single SnO2nanowire electrode［J］. Science，2010，330 (6010):1515.

［3］ Garcia-Mateo C，Caballero F G，Capdevila C，et al.Estimation of dislocation density in bainitic microstructures using high-resolution dilatometry ［J］. Scripta Mater.，2009，61(9):855.

［4］ Goland A N，Keatino D T. Lattice parameter，volume，and length changes in crystals containing dislocation loops［J］. J. Appl. Phys.，1970，41(2):814.

［5］ Jensen E J，Damgaard-Kristensen W，Cotteril M J.Molecular dynamics studies of melting:I. Disloca-tion density and the pair distribution function［J］. Philos.Mag.，1973，27(3):623.

［6］ Chen Z L，Xu W R，Tang L D. The theory and practice of molecular simulation ［M］. Beijing:Chemical Industry Press，2007 (in Chinese)［陈正隆，徐为人，汤立达. 分子模拟的理论与实践［M］. 北京:化学工业出版社，2007］

［7］ Foiles S M，Baskes M I，Daw M S. Embedded-atommethod functions for the fcc metals Cu，Ag，Au，Ni，Pd，Pt，and their alloys［J］. Phys. Rev. B，1986，33(12):7983.

［8］ Wang R，Fang Q F. Core structure and mobility of an edge dislocation in aluminum［J］. J. Alloys Compd.，2000，310(1-2):80.

［9］ Doyama M，Kogure Y. Computer simulation of creation and motion of dislocations during plastic deformation in copper［J］. Mater. Sci. Eng. A，2001，309 -310:451.

［10］ Hull D，Bacon D J. Introduction to dislocations［M］.5rd ed，2011.

［11］ Gehlen P C，Hoagland R G，Hirth J P. Flexible boundary conditions and nonlinear geometric effects in atomic dislocation modeling ［J］. J. Appl. Phys.，1978，49(7):3890.