混合流体Rayleigh-Benard对流研究进展

李开继,宁利中,王 娜,王永起,胡 彪

(西安理工大学 西北旱区生态水利工程国家重点实验室培育基地,西安 710048)

混合流体Rayleigh-Benard对流研究进展

李开继,宁利中*,王 娜,王永起,胡 彪

(西安理工大学 西北旱区生态水利工程国家重点实验室培育基地,西安 710048)

在介绍混合流体Rayleigh-Benard(RB)对流的研究手段的基础上，回顾了混合流体RB对流的线性稳定性分析，对流发生点附近的“闪烁”(Blinking)行波，以及沿着对流分叉曲线的上部分支，随着对流参数的变化而得到的几种混合流体行波对流斑图的研究成果。最后，总结了近年来关于水平流动对RB对流影响的研究成果并进一步对混合流体RB对流的前景提出了展望。

混合流体；Rayleigh-Benard；线性稳定性；“闪烁”行波；进展

0 引 言

RB对流是研究对流问题的经典流体力学模型之一，揭示了极为丰富、有趣的线性以及非线性动力学现象。1900年Benard首次发现了纯流体的热对流运动的现象。1916年Rayleinh[1]在Navier-Stokes方程的基础上建立了热浮力驱动流体运动的运动方程，后来，称由热浮力引起的热对流为RB对流，并建立了RB对流模型。在随后的近百年里RB对流模型系统的研究得到了蓬勃发展。直到20世纪80年代，对于分离比ψ<0的混合溶液的对流运动现象引起了学者重视，当其上下壁面之间的温度梯度大于临界值后将产生向某一固定方向滚动的对流，此后，RB对流模型系统的研究重心开始由对纯流体的研究转向对混合流体的研究。由于对混合流体RB对流研究的时间较短，相应的综述类文章也相对很少，王涛[2]仅对一小部分混合流体的实例进行了分析。本文将针对混合流体，根据文献[3]给出的沿着混合流体对流分叉曲线上部分支，随着对流参数变化在矩形腔体内观察到的几种行波来介绍混合流体RB对流的研究进展。

1 研究手段

1.1 实验手段

早期,通过实验观测了对流的结构及其形成过程,探讨了尺寸效应、边界效应、混沌结构等特性。观测RB系统混合流体对流运动的典型实验装置见图1,可以简单地描述如下：a表示实验空腔的端壁；A是实验中充满混合流体的腔体；b、c是形成腔体、控制腔体上下层温度的铜板，为了使b、c的温度恒定，其面积为腔体面积的10倍以上。B、C是保持上下铜板b、c温度恒定的循环水系统，c为加热部件，通过腔体层将热传输到b，b是吸热部件。

图1 实验装置Fig.1 Sketch map of the experimental device

在实验观测方面有许多方法,包括烟流法、干涉成像法、纹影法、热敏液晶显示法和观测二维速度场的PIV法等。

1.2 从模型方程探讨混合流体Rayleigh-Benard对流的非线性

后来通过模型方程探讨非平衡区域中的混合流体对流运动。在弱非线性的假定下,在分叉点附近通过级数展开等方法,人们已建立了各种模型方程或振幅方程，包括Ginzbarg-Landau方程、复数GL方程、耦合GL方程、Kuramoto-Sivashinsky方程、Swift-Hohenberg方程等。

Cross等人为了计算混合流体的对流运动，将GL方程扩展到了具有行波解的TDGL型方程组,但分叉曲线仍是超临界的[4]。Sullivan[5]进一步将振幅方程扩展到五次项，形成了与混合流体对流一致的亚临界分叉曲线，并且可以摸拟一些对流斑图。王卓运等[6]对GL方程形式再次进行了化简,为：

(1)

(2)

式中A，B为行波对流的振幅；υ反映群速度；ε反映相对瑞利数；g代表非线性系数。在计算中往往采用两个方程进行耦合计算。Zaks等[7]利用振幅方程，对摆动行波(UTW)的摆动特性及其稳定性进行了研究。Riecke等[8，9]推导了一系列对流振幅和浓度模型的耦合方程，但是只求得了局部行波解，并未给出浓度分布的复杂结构。

1.3 数值模拟

混合流体RB对流的常规数值方法有：有限差分法、有限元法、有限体积法以及谱方法等，而有限体积法和谱方法近些年来比其他方法更为流行,特别是有限体积法已成为数值研究腔内RB对流最为流行的方法,也是各种商用软件的首选。

1.3.1 流体力学方程组

底部受热的窄长腔体中充满混合流体的物理数学模型见图2。简单地描述如下:流体位于薄层封闭容器(长度为Lx，高度为d)内，顶部恒温T0，底部加热T=T0+△T。冷热羽流自组织形成环流。布辛涅斯克(Boussinesq)近似假设如下：

(3)

描述这一问题的流体力学方程组可写为：

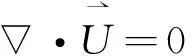
(4)

(5)

(6)

(7)

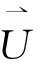
图2 对流滚动示意图Fig.2 Sketch map of convection roll

1.3.2 扰动方程组

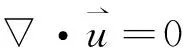
(8)

(9)

(10)

(11)

2 线性稳定性分析

流体流动的稳定性一直是流体力学的中心问题之一，而边界层的稳定性是RB对流的一个重要现象,因此理解边界层内对流运动在什么条件下会从

一个流动状态转换成另外一个流动状态是腔内对流研究的一个重要方向，因而线性稳定性分析就成为研究边界层稳定性的一个重要且有效的方法。1957年，Plapp为了研究边界层的不稳定性提出了“平行性假设”。由于“平行性假设”的局限性，Bertolotti[14]给出了线性稳定性分析方法、Herbert[15]给出了直接稳定性分析方法和Brooker[16]给出了求解抛物性稳定性方程(PSE)等方法来替代“平行性假设”。此外，又考虑到近壁面的流体物性参数的变化，Severin[17]进一步给出了求解抛物性稳定性方程和改进Orr-Sommerfeld方程(EOSE)的比较性分析法。李国栋[18]等人又采用扰动方法和运用模态分析理论对对流发生临界点附近的对流进行了线性稳定性研究和分析:当分离比ψ<0时，其振荡频率随分离比绝对值的增大而增大，随普朗特数Pr的增大而减小。与纯流体相比,临界Rayleigh随分离比绝对值的增大而增大,表明混合成分索雷特效应增加了系统的稳定性。同时，分离比绝对值越小，对流发生越容易。Hu[19]等利用Chebyshev多项式方法进一步研究了很大Reynolds数下Poiseuille-Rayleigh-Benard流动的稳定性，给出了与文献[18]相同的线性稳定性分析结果。

3 混合流体的行波对流时空结构及其特性

对于分离比ψ<0的混合流体，RB对流系统会在对流发生点附近出现振动对流,然后经过一个亚临界的Hopf分叉到达时间依赖的行波对流状态，这是因为浓度扩散比温度扩散慢得多而形成的。沿着鞍结分叉点以上的上部分支，随着对流参数的变化会出现许多有趣的对流结构，比如：局部行波、具有缺陷的行波、对传波、均匀行波、摆动行波和定常对流或准定常对流。由文献[3]的计算结果说明了，沿着鞍结分叉点以上的上部分支上获得的这几种斑图的振幅是连续变化的，没有跳跃现象。相对瑞利数从小增大与从大减小，沿分叉曲线计算的斑图转换点是不一致的，似乎存在迟滞现象[3,11]。

3.1 对流临界点附近的特性

为了研究发生对流的起因、状态、相变以及对流的稳定性等因素，文献[20]对对流发生临界点附近的对流特征进行了详细客观的研究,发现鞍结点与对流发生临界点之间亚分叉曲线的下部分支是一段不稳定的区间，并且该段的对流振幅随相对瑞利数的增加而迅速增加，呈近似垂直线行分布。Batiste[21]和文献[22]发现在对流发生临界附近会出现一种非常有趣的“闪烁”状态的行波。为了更加清楚、明确的反映Onset附近对流特征，分别对Nusselt数(反映的是通过流体层的总的垂直热通量)、行波的相速度(描述行波的运动特性)、混合参数M进行了探讨，发现在鞍结点与对流发生临界点之间，特征量Nusselt数随相对瑞利数的增加而迅速增加，呈近似垂直线行分布；相速度随相对瑞利数的增加迅速减小，呈近似垂直线行分布，在鞍结点附件相速度为最大值；混合参数M也是随相对瑞利数的增加迅速减小，呈近似垂直线行分布。Sullivan[23]研究了不同普朗特数Pr下，Rayleigh数与分离比ψ的依赖关系，发现随着普朗特数的增大，对流发生临界点处的Rayleigh数也增大；在同一普朗特数下，负分离比的绝对值越大，临界点处的Rayleigh数越大。

3.2 对流分叉点附近的Blinking行波状态

对于混合流体，当从下面加热时，会表现出各种各样的行为，特别是分离比ψ<0的弱索雷特效应条件下的混合流体，如果这个分离比足够负，在对流分叉点附近会出现一种非常有趣的与复杂时空结构相依附的“闪烁”状态的行波,比如对流振幅随时间变化的“闪烁”行波状态。Deane[24]通过数值模拟的方法第一次观察到了“闪烁”状态的扩散对流现象。随后，Kolodner[25]在混合流体对流实验中也观察到了“闪烁”状态的扩散对流现象，这说明“闪烁”行波是存在的，并且在混合流体中也是存在的。同时还揭示了“闪烁”状态的动力学对于系统的长高比Γ和Rayleigh数的依赖性。宁利中[22，26]和Batiste[27]采用数值模拟的方法对分离比ψ<0的弱索雷特效应条件下对流临界点附近的交替“闪烁”状态的行波进行了研究，发现它的主要特征是对流从中心附近开始向两侧传播，但向两侧传播的对流振幅随时间交替成长并且对流控制的区域也在交替的变化。同时，还发现由于其发生在临界点附近且振幅很小，因此“闪烁”行波对流是一种弱非线性结构。Batiste[27]还阐明了交替“闪烁”状态的起源。Kolodner[25]发现，在某些情况下，缺陷源水平运动的对传波还可以过渡成稳定且具有弱非线性结构的“闪烁”行波。

3.3 局部行波对流和双局部行波对流

为了观察分离比ψ<0混合流体的对流现象,实验工作者采用了矩形窄长容器装置来观测一维对流现象，利用这种装置Moses等[28]和Heinrichs等[29]人获得了一种被称为局部行波(局部行波指在均匀的上、下壁面温度差的条件下,局部区域存在对流运动,而其它区域无对流存在)的对流斑图。Kolodner[30]通过实验研究了局部行波的稳定性形态、对流中脉冲部分的运动情况以及它们内在的扰动，发现局部行波依赖于Rayleigh数。此后,实验工作者还观测获得了不同构造的局部行波状态，其中比较典型的是Harada[31]在矩形合子中观测到的双局部行波。后来，Jung[32]等人通过数值模拟的方法获得了局部行波的对流场、温度场、速度场等细部结构。王涛[33]等人采用高精度数值模拟,对双局部进行波的研究进行了扩充，并讨论了双局部行波的动力学特性。不论采用何种研究手段，得出共同结论有：

1)在中等长高比腔体内，Yahata[34]利用流体力学扰动方程组讨论了小分离比条件下局部行波的对流结构和动力学特性。文献[35]用数值模拟的方法探讨了局部行波的稳定性,通过进一步增加相对瑞利数，获得了混合流体的局部行波对流斑图(图3)，发现局部行波的主要特征有：行波区域只存在于腔体的一端，另一端是传导状态，这种对流形式与Kolodner[25]得到的一样。如果继续增加相对瑞利数,发现行波区域所控制的长度明显增加,传导区域明显减小，当相对瑞利数增加到某一值时,局部行波失去稳定，由局部行波转化为均匀的定常行波。

图3 局部行波对流斑图Fig.3 Localized traveling wave convection pattern

2)在大长高比腔体内，Aolnsoa[36]研究了环形腔体内的混合流体对流结构以及其动力学特性。文献[37]通过进一步增加相对瑞利数,获得了双局部行波对流的对流斑图(图4)，发现双局部行波区域存在于腔体的两端，中间部分是传导状态。如果继续增加相对瑞利数,发现行波区域所控制的长度明显增加,传导区域明显减小。还探讨局部状态对Rayleigh数的依赖性,Kolodner[25]、文献[37]计算了在不同Rayleigh数下,容器高度1/2处的温度场的空间变化，发现随着相对瑞利数的增加局部行波区域的宽度也在增加。王涛[33]等人采用高精度数值模拟法也得到了相同的结果。

图4 双局部行波对流斑图Fig.4 Doubly localized traveling wave convection pattern

3)为了分析双局部行波的动力特性,文献[37]对一个时间周期上的行波场进行了时间平均,获得了容器高度1/4处的温度场与浓度场分布曲线图(图5)。发现温度场在行波区域为负的类似于包络线的分布,传导区域温度场为零。而浓度场在中间的传导区域接近于零,两侧的行进波区域为正的分布,类似于包络线分布。这一特性说明在一个时间周期上的双局部行波的平均值可以很好的表征局部行波的特性。在以下图中，x表示腔体长度，t表示时间。

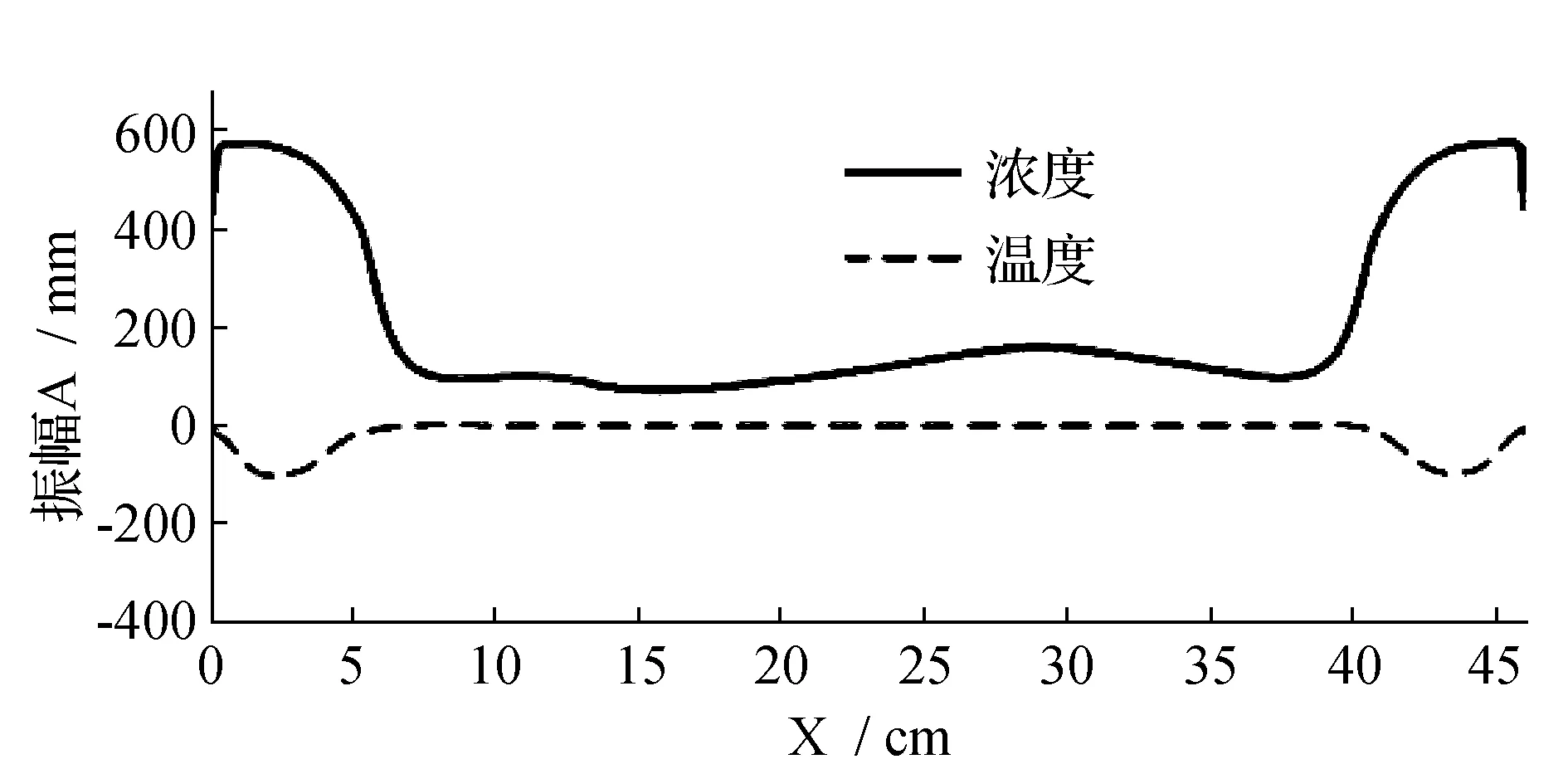
图5 一个周期上的平均温度场与浓度场的分布曲线图Fig.5 The distribution curve of the average temperature field and concentration field in a cycle

3.4 有缺陷的行波对流

当局部行波达到稳定后，继续增加相对瑞利数到达某个值的范围内以后，在某个时刻，腔体内行波的某一个滚动的相位会突然发生180°的转变，在它的两侧会各有一个新的滚动产生，形成一种有“缺陷”的结构，这样的现象称其为有缺陷(defect)的行波对流现象，见图6。如果相对瑞利数继续增加，缺陷就会逐渐消失过渡到无缺陷的状态。对于有缺陷的混合流体行波对流，前人通过不同的研究手段已做出了一些研究成果,如Kolodner[38-39]等人在环形腔体内通过实验获得了一种具有时空错位缺陷的行波对流，具有缺陷的局部行波对流和空间位置固定的缺陷连续出现的源和汇式的行波对流。Bensimon[40]等人也在环形腔体内通过实验手段发现了空间位置固定的缺陷连续出现的源(Source)和汇(Sink)式的行波对流斑图。Coullet[41]等利用耦合的Landau-Newell型方程组获得了时空缺陷连续出现的源和汇式的行波对流斑图。笔者通过数值模拟的方法在矩形腔体内研究了一个缺陷位置固定并连续出现的汇式的行波对流[42-44]，缺陷源水平移动的对传波和中等索雷特效应的对流系统中具有间歇缺陷的行波对流[45]。Aegerter[46]对侧边界条件上的行波对流斑图相缺陷的影响进行了详细的描述。在前人研究的基础将含有缺陷的行波对流的稳定性及其动力学特性总结如下：

1)分离比ψ对含有缺陷的行波对流的影响。分离比ψ反映了系统的索雷特效应，也就是温度场对浓度场的诱导情况。它的大小会直接影响对流发生临界点和分叉形态。因此，也必然会影响行波对流系统及含有缺陷的行波对流的特性，也会影响各斑图之间的形成、过渡与转化。Kolodner[38]研究了分离比ψ对含有缺陷的行波对流的影响，研究发现，对于不同的分离比ψ，其所对应的含有缺陷的行波对流的缺陷发生周期TP也不同。当负分离比较大时,缺陷出现的周期TP较小，含有缺陷的行波对流存在的区间较大,而随着负分离比ψ的减小,缺陷出现的周期TP急剧变大，含有缺陷的行波对流存在的稳定区间减小。继续减小负分离比，ψ到某个值时,会发现缺陷消失。

2)Rayleigh数对缺陷的影响。为了探讨Rayleigh数对具有缺陷行波的影响，Kolodner[38-39]等人、Bensimon[40]等人、我们小组[42-44]对不同相对瑞利数情况下的含有缺陷的行波对流进行了计算，发现缺陷出现的时间间隔不是固定的，它随着相对瑞利数的增大而增大，同时，随着相对瑞利数的增大对流振幅次数和缺陷出现的周期也在增加。

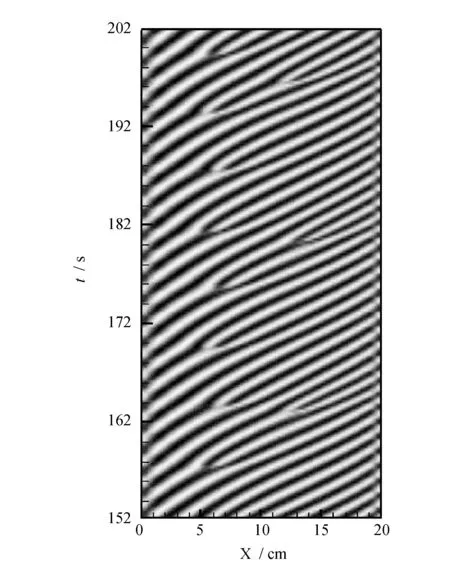
图6 有缺陷的行波对流斑图Fig.6 Traveling wave convection pattern with defects

3.5 缺陷源水平运动的对传波

随着相对瑞利数的变化，Riecke[47]和Batiste[48]在对流发生点附近发现，当行波对流结构中的缺陷结构消失以后，如果继续增大相对瑞利数，就会出现一种更为有趣的瞬态的对流结构—缺陷源水平运动的对传对流结构。后来，Moses等在实验中，也得到了对传源缺陷水平运动的现象(DefectSourceofCounterPropagatingWave,系指对传波波源处的缺陷)[12]。1993年，Kaplan[49]等人在侧向加热情况下也获得了缺陷源水平运动的对流现象。文献[44]在对流发生的临界点附近也发现了缺陷源水平移动的对传波对流现象,发现缺陷源水平运动的对传波具有一定的稳定性。2008年，郝建武[50]等人通过流体力学基本方程组的数值模拟获得了一种新的有趣斑图，即单侧缺陷摆动对传波，发现单侧缺陷摆动对传波的缺陷源始终在偏离腔体一侧端壁保持距离不变的某一小范围内作“S”型曲线摆动，摆动幅度很小。王涛[51]等人对腔体内的缺陷源水平运动的对传波对流进行了高精度数值模拟，研究了缺陷源水平运动的对传波在经历了瞬态的对传状态、调制对传状态、定常状态。发现Rayleigh数对行波有一定的影响：系统进入定常行进波的时间随着Rayleigh数的增大而减小,在其它参数一定的条件下，对流振幅整体上随着Rayleigh数的增大而增大。

3.6 均匀的行波

继续增大相对瑞利数，Kolodner[52]发现，相对瑞利数到达某个范围内以后，行波中的缺陷就会逐渐消失，行波对流滚动充满整个腔体，并以一定的速度向左或右传播，传波速度保持不变，称这样的行波为均匀行波(图7)。Kolodner[52]发现Rayleigh数对传波速度有一定的影响：传波速度随Rayleigh数的增加而较小。Barten[53-54]等人计算了周期条件下均匀行波场的结构以及相应的动力学特性,进一步讨论了在一个环形盒子(或者周期边界)与小分离比条件下局部行波的形成过程及局部行波场的结构。王涛[55]等人对腔体内的混合流体RB对流进行了高精度数值模拟,研究了具有较弱索雷特效应下，附加一个微小的温度扰动作为扰动源的中等长高比腔体内混合流体对流系统中时空结构的发展。

图7 均匀行波对流斑图Fig.7 Uniform traveling wave convection pattern

3.7 摆动行波

前人发现沿着混合流体对流运动分叉图的非线性分支从均匀行波状态向定常对流状态的过渡并不是直接的,而是应该还存在一种未被发现的行波，一般发生在从均匀行波对流向定常对流过渡时的某个参数范围内。为了解决这一问题，Sullivan进行了大量的研究，Sullivan[56]通过改变参数Rayleigh数在腔体内发现了一种存在均匀流和定常流之间的行波(图8)，它在向一个方向传播一段时间后,会突然改变方向向相反的方向传播，再经过一段时间后，传波方向会再次改变，这样反复改变传播方向不停地向前运动,他将保持这种对流状态的对流结构称之为摆动行波。摆动行波是一种具有强非线性结构的行波，是一种非常有趣的对流结构。Bodenschatz在液晶的电流体对流中，Clever等在具有水平流动的Rayleigh-Benard对流中及Busse在倾斜的对流层中，也发现了摆动行波现象[57]。后来，Zaks[7]利用振幅方程又研究了摆动行波及其稳定性，发现随着时间的增加，靠近腔体的一端壁附近不断地有新的滚动生成，而在腔体的另一端壁附近不断地有滚动消失，但腔体中的滚动个数却始终保持不变。宁利中发现混合流体RB对流中在均匀行波对流向定常对流过渡的过程中存在摆动行波对流现象[58]。探讨了混合流体摆动行波对流的形成过程、时空结构、动力学特性及分离比对摆动对流的影响[59-62]。发现:

1)摆动行波对Rayleigh数有一定的依赖性：摆动周期随Rayleigh数增大而减小；对流振幅和Nusselt数随Rayleigh数的增大而增加。

2)分离比ψ对摆动行波对流有一定的影响：摆动行波对流的存在区间随分离比绝对值减小而减小，随相对瑞利数增加而减小；当负分离比的绝对值较大时，周期性的摆动行波对流存在的区间也比较大，而随着负分离比绝对值的减小，周期性的摆动行波对流存在的稳定区间也减小，同时，摆动行波对流摆动的幅度也减小。

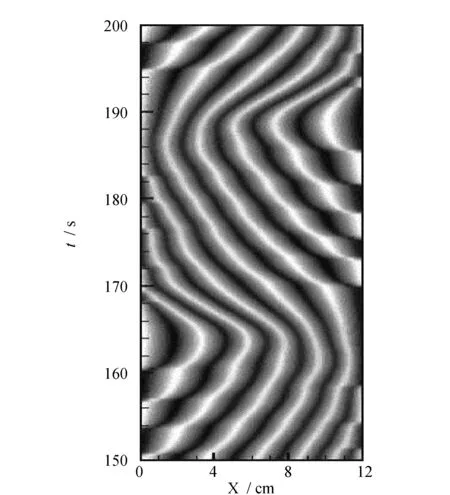
图8 摆动行波对流斑图Fig.8 Undulation traveling wave convection pattern

齐昕[62]对具有较强索雷特效应(分离比ψ=-0.47)的混合流体在极小长高比(Γ=4)腔体内的摆动行波对流运动情况进行了模拟研究，探讨了摆动行波的动力学特性，获得了稳定的摆动行波的摆动周期TP的变化规律：Tp随相对瑞利数的减小而逐渐增大。还分析了极小长高比行波对流对相对瑞利数的依赖性及稳定性:随着Rayleigh数的减小，摆动行波沿时间方向摆动的振幅在逐渐增加，摆动越来越明显，摆动周期也在增加。

3.8 定常流(SOC)

当相对瑞利数超过某个临界值，随着时间的增加，腔体内的特性参数不再振荡，而是趋于定值，此时腔体内出现定常对流，即对流滚动随时间不再向左或向右传播，而是在原来的位置连续滚动。由文献[3，18，20，35]的研究发现定常流对分离比ψ有一定的依赖性：分离比ψ不同时腔体内产生的滚动圈的个数也不同，并且是负分离比越小滚动圈的个数越多。还发现定常流对相对瑞利数也有一定的依赖性及稳定性：随着相对瑞利数的增大，定常流对流状态越容易达到稳定态，也就是说从不稳定状态到稳定状态的过渡时间越短。

4 水平流动对Rayleigh-Benard对流的影响

水平流动作用下的Rayleigh-Benard对流系统研究可以解决地球物理问题,比如天空中云的形成,陆地上沙丘的形成,以及海洋中海岛的形成等。Lucke小组[63-64]、石峯[65]、李国栋[66-67]、赵秉新[68]等人对受水平流动作用下的混合流体RB对流进行了研究，发现当水平流动与混合流体RB对流相耦合时，与单一的纯流体RB对流运动和经典的混合流体RB对流都不同，其时空结构和对流特性更为丰富和复杂(比如温度场、浓度场、速度场的结构和对流斑图不但表现出空间的周期性，同时也表现出时间的周期性[68])，它构成了另一个有趣的系统。文献[26]发现水平流动与RB对流运动相耦合,会出现两种新的对流结构:绝对不稳定状态下的行波对流和局部行波对流以及对流不稳定状态下的局部行波对流。Harada[31]并在给定的分离比下分析了周期性局部行波对Rayleigh数和水平流强度Reynolds数的依赖性。后来，石峯[65]又讨论研究了在二维矩形腔体中，不同来流形式和强度与RB对流耦合作用的结构斑图和特性，对比分析了水平流及脉冲流与RB对流耦合作用的结构：发现当水平来流与RB对流耦合作用时，对流结构既表现空间周期性，同时也表现时间周期性；而当水平脉冲流与RB对流耦合作用时，对流滚动受到脉冲流的影响发生左右摆动，对流可以向上下游两侧传播，摆动也表现出周期的特性。Lucke小组先于1996年对该系统的线性稳定性进行了分析[63]，结果表明水平的流动作用破坏了对称的左右行波分叉分支,它们的临界特性依赖于流动强度Reynolds数。该小组在2000年的研究又表明水平流动作用会改变系统的非线性分叉特性[64]，从而形成所谓的对称破缺分叉。李国栋进一步对水平流动作用对混合流体Rayleigh-Benard对流分叉的影响及稳定性进行了研究[66]，数值模拟了在极其微弱的水平流动作用下,混合流体Rayleigh-Benard对流一维行波斑图的成长及其时空演化问题[67]。赵秉新[68]利用高阶紧致有限差分格式，数值模拟研究了物性参数对具有索雷特效应的混合流体的Poiseuille-Rayleigh-Benard流动系统的影响,进一步探讨了水平流强度和Rayleigh数对流场结构的影响。另外，文献[31,65]还讨论了临界特性对流动强度Reynolds数的依赖性：顺行波的临界分叉值随Reynolds数的增大一直单调递增，而逆行波的临界分叉值则正好相反。文献[65-66，68]发现了对流振幅与水平流动强度Reynolds数的依赖关系(即稳定性)：随着水平流动强度的增强，RB对流运动的振幅减小。文献[65,67]揭示了行波对流的周期性对水平流动强度的依赖性：增大Reynolds数时,行波重复的周期会不断下降，特别是在Reynolds数很小时,其变化对水平流强度的改变非常敏感。随着Reynolds数的减小,对流的周期变得越来越长。如今,这项研究又应用到了新的领域,比如微电子领域和化学领域等。

5 结论与展望

本文对沿着分叉曲线的上部分支，随着相对瑞利数的增加,在矩形腔体内观察到的几种行波对流结构以及特性进行了归纳和总结。重点是介绍对流流动对瑞利数、普朗特数和腔体高宽比的研究进展。也探讨Rayleigh数对具有缺陷行波的影响；对流振幅与水平流动强度Reynolds数的依赖关系。最后,总结了水平流动对RB对流的影响。以上的归纳和总结旨在呈现该类问题的研究现状，发现存在的不足，以便进一步推进该研究方向的发展。

在基础研究方面，热腔内流动和传热对控制参数普朗特数和腔体高宽比的依赖仍然需要深入的理解,特别是不同性质的流动间的演化对普朗特数和高宽比依赖的定量关系还未确定,需要进一步的研究；数值模拟的精度偏低，还有极大的提高空间；控制手段对流体力学机制还需深入的认识,特别是诱导出的层流、湍流的定量关系。

由于混合流体行进波对流研究的时间较短,仍有许多问题需开展研究。例如:①近年都选取的是平面矩形腔体(即二维腔体)进行研究，可进行混合流体Rayleigh-Benard对流运动的三维数值模拟，并对比与二维计算结果的差异及影响;②研究在不同外力条件下的混合流体RB对流的特性(如在磁力场中RB对流的稳定性和动力学特性);③探讨初始条件对行波对流斑图的影响;④具有Dufour效应的混合气体在各种热边界条件下的稳定性与动力学特性;⑤探索其他消除对流腔体中部的时空缺陷的方法。

[1]RayleighL.Onconvectioncurrentsinahorizontallayeroffluidwhenhighertemperatureisontheunderside[J].Philos.Mag.,1916,32:529-546.

[2]王 涛.混合流体对流运动的研究进展[J].西南民族大学学报:自然科学版,2007,33(6):1 395-1 399.

[3]宁利中，余 荔，袁 哲，等.沿混合流体对流分叉曲线上部分支行波斑图的演化[J].中国科学G,2009,39(5):746-751.

[4]GetlingAV.Rayleigh-Benardconvection[M].London:WorldScientific,1998.

[5]SullivanTS,DeisslerRJ.EliminationofhysteresisinasystemofcoupledGinzburg-Landauequation[J].Phys.Rev.A,1989,40:6 748-6 751.

[6]王卓运，宁利中，王 娜，等.基于振幅方程组的行波对流的数值模拟[J].西安理工大学学报,2014,30(2):163-169.

[7]ZaksMA,AuerM,BusseFH.UndulatingrollsandtheirinstabilitiesinaRayleigh-Benardlayer[J].Phys.Rev.Lett.,1996,E53(5):4 807-4 819.

[8]Riecke.Self-trappingoftraveling-wavepulsesinbinarymixtureconvection[J].Phys.Rev.Lett.,992(68):301-304.

[9]RieckeH.Coexistingpulsesinamodelforbinary-mixtureconvection[J].Phys.Rev.Lett.,1995,75(22):4 035-4 038.

[10]NingLizhong.Travelingwaveconvectioninbinaryfluidmixtures[M].Tokyo:ABellandHowellCompany,1999.

[11]NingLizhong,HaradaY,YahataH.Transitionofconvectionpatternsinarectangularcell[J].J.Hydrodyn.,2001,13(4):65-71.

[12]NingLizhong,HaradaY,YahataH.Fully-developedtravel-ingwaveconvectioninbinaryfluidmixtureswithlateralflow[J].Prog.Theor.Phys.,2001,106(3):503-512.

[13]PlappJE.Theanalyticstudyofthelaminarboundarylayerstabilityinfreeconvection[J].Aeron.Sci.,1957,24:318-319.

[14]BertolottiFP,HerbertT,SpalartPR.LinearandnonlinearstabilityoftheBlasiusboundarylayer[J].J.FluidMech.,1992,242:441-474.

[15]HerbertT.Parabolizedstabilityequations[J].Annu.Rev.FluidMech., 1997,29:245-283.

[16]BrookerAMH,PattersonJC,ArmfilidSW.Non-parallellinearstabil-ityanalysisoftheverticalboundarylayerinadifferentiallyheatedcavity[J].J.FluidMech.,1997,352:265-281.

[17]SeverinJ,HerwigH.Higherorderstabilityeffectsinanaturalcon-vectionboundarylayeroveraverticalheatedwall[J].HeatMassTransfer,2001,38:97-110.

[18]李国栋,田飞飞,宁利中,等.混合流体Rayleigh-Benard对流的线性稳定性分析[J].水动力学研究与进展,2010,25(4):446-452．

[19]HuJun,HadidHB,HenryD.LinearstabilityanalysisofPoiseuille-Rayleigh-Benardflowsinbinaryfluidswithsoreteffect[J].Phys.Fluids,2007,19(3):034101.

[20]宁利中，王 娜，袁 喆，等.分离比对混合流体Rayleigh-Benard对流解的影响[J].物理学报,2014,63(10):104401.

[21]BatisteO,KnoblochE,MercaderI,etal.Simulationsofoscillatorybinaryfluidconvectioninlargeaspectratiocontainers[J].Phys.Rev.E,2002,65(1):016303．

[22]宁利中，袁 喆，石 峯，等.具有强Soret效应的充分发展的混合流体行进波对流[J].应用力学学报,2007,24(3):363-367.

[23]SullivanTS,AhlersG.Hopfbifurcationtoconvectionnearthecodimension-twopointina3He-4Hemixture[J].Phys.Rev.Lett.,1988, 61(1):78-81.

[24]DeaneAE,KnoblochE,ToomreJ.Travelingwavesinlarge-aspect-ratiothermosolutalconvection[J].Phys.Rev.A,1988,37(5):1 817-1 820.

[25]KolodnerP,SurkoCM.Weaklynonlineartraveling-waveconvection[J].Phys.Rev.Lett.,1988,61(7):842-845.

[26]NingLizhong,HaradaY,YahataH,etal.Numericalsimulationoftravelingwaveconvectioninaweaklynonlinearregime[J].JHydrodyn.,2000,12(2):20-30.

[27]BatisteO,NetM,MercaderI,etal.Oscillatorybinaryfluidconvectioninlargeaspect-ratiocontainers[J].Phys.Rev.Lett.,2001,86(11): 2 309-2 312.

[28]MosesE,FinebergJ,SteinbergV.Multistabilityandconfinedtraveling-wavepatternsinaconvectingbinarymixture[J].Phys.Rev.,1987,A35,2 757-2 760.

[29]HeinrichsR,AhlersG,CannelDS.Travelingwavesandspatialvariationintheconvectionofabinarymixture[J].Phys.Rev.,1987,A35:2 761-2 764.

[30]KolodnerP.Stable,unstableanddefectedconfinedstatesoftraveling-waveconvection[J].Phys.Rev.E,1994,50:2 731-2 755.

[31]HaradaY,MasunoY,SugiharaK.Traveling-waveconvectioninbinaryfluidmixturesandspatiotemporalstructure[J].VistasinAstronomg, 1993,37:107-110.

[32]JungD,LuckeM.Localizedwaveswiththeexistenceofextendedwaves:Oscillatoryconvectionofbinarymixtureswithstrongsoreteffect[J].Phys.Rev.Lett.,2002,89(5),054502.

[33]王 涛，葛永斌．双局部行进波对流的高精度数值模拟[J].合肥工业大学学报：自然科学版，2012,35(6):842-847.

[34]YahataH.Travelingconvectionrollsinabinaryfluidmixture[J].Prog.Theor.Phys.,1991,85:933-937.

[35]宁利中,原田义文,八幡英雄.中等长高比腔体内的局部行进波对流[J].水动力学研究与进展,2004,19(4):469-474.

[36]AlonsoaA,BatisteO,MercaderI.Numericalsimulationsofbinaryfluidconvectioninlargeaspectratioannularcontainers[J].Eur.Phys.J.,SpecialTopics,2007,146:261-277.

[37]宁利中,原田义文,八幡英雄.双局部行进波对流的时空结构[J].水利学报，2004,12:56-61.

[38]KolodnerP,BensimonD,SurkoCM.Traveling-waveconvectioninanannulus[J].Phys.Rev.Lett.,1998,60(17):1 723-1 726.

[39]KolodnerP.Extendedstatesofnonlineartraveling-waveconvection.Ⅱ.Frontsandspatiotemporaldefects[J].Phys.Rev.A,1992, 46(10):6 452-6 468.

[40]BensimonD,KolodnerP,SurkoCM,etal.Competingandcoexistingdynamicalstatesoftraveling-waveconvectioninanannulus[J].J.FluidMech.,1990,217:441-467.

[41]CoulletP,ElphickC,GilL,etal.Topologicaldefectsofwavepatterns[J].Phys.Rev.Lett.,1987,59(8):884-887.

[42]NingLZ,HaradaY,YahataH.Formationprocessofthetraveling-wavestatewithadefectinbinaryfluidconvection[J].Prog.Theor.Phys. 1997,98(3):551-556.

[43]宁利中，齐 昕，周 洋，等.混合流体Rayleigh-Benard行波对流中的缺陷结构[J].物理学报,58(4):2 529-2 534.

[44]宁利中,齐 昕,石 峯,等.具有间歇性缺陷的混合流体行进波对流斑图[J].力学季刊,2008,29(1):1-7.

[45]NingLizhong,QiXin,YuanZhe,etal.Acounterpropagatingwavestatewithaperiodicallyhorizontalmotionofdefects[J].J.Hydrodyn., 2008,20(5):567-573.

[46]AegerterCM,SurkoCM.Influenceoflateralboundaryconditionsonaphase-defectdescriptionoftraveling-waveconvectionpatterns[J].Phys.SectionD,2002,166(3):155-166.

[47]RieckeH,KramerL.Thestabilityofstandingwaveswithsmallgroupvelocity[J].Phys.D:NonlinearPhenomena,2000,1-2(137):124-142.

[48]BatisteO,KnoblochE,MercaderE.etal.Simulationsofoscillatorybinaryfluidconvectioninlargeaspectratiocontainers[J].Phys.Rev.E,2002,65(1):016303.

[49]KaplanE,SteinbegV.Phaseslippagenonadiabaticeffectanddynamicsofasourceoftravelingwaves[J].Phys.Rev.Lett,1993,71(20):3 291-3 294.

[50]郝建武，宁利中，王卓运，等.长矩形截面腔体内具有缺陷的对传行波斑图[J].力学季刊,2013,34(1):139-146.

[51]王 涛，葛永斌.微小扰动下中等长高比腔体内行进波对流的高精度数值模拟[J].合肥工业大学学报：自然科学版,2012,35(11):1 569-1 573.

[52]KolodnerP.Repeatedtransientsofweaklynonlineartraveling-waveconvection[J].Phys.Rev.E,1993,47(2): 1 038-1 048.

[53]BartenW,LuckeM,KampsM,etal.ConvectioninbinaryfluidmixturesI.Extendedtravelingwaveandstationarystates[J].Phys.Rev.E,1995,51:5 636-5 661.

[54]BartenW,LuckeM,KampsM,etal.ConvectioninbinaryfluidmixtureⅡ.Localizedtravelingwaves[J].Phys.Rev.E,1995,51:5 662-5 680.

[55]王 涛，田振夫，葛永斌．长腔体内混合流体行进波对流的高精度数值模拟[J]．水动力学研究与进展:A辑,2011,26(1):41-47.

[56]SullivanT,AhlersG.Nonperiodictimedependenceattheonsetofconvectioninabinaryliquidmixture[J].Phys.Rev.A,1988,38 (6):3 143-3 146.

[57]BusseFH,AuerM.Undulatingrollsanddomaininstability[J].Phys.Rev.Lett.,1994,72(20):3 178-3 181.

[58]NingLizhong.Travelingwaveconvectioninbinaryfluidmixtures[D].FukuiUniversity,Fukui,Japan,1998.

[59]宁利中,齐昕,王思怡,等.小长高比腔体内的摆动行波[J].应用力学学报,2010,27(3):538-542.

[60]宁利中,齐 昕,余 荔,等.两种类型的摆动行波对流[J].水动力学研究与进展,2011,(26)5:524-530.

[61]余 荔,宁利中,魏炳乾,等.Rayleigh-Benard对流及其在工程中的应用[J].水资源与水工程学报,2008,19(3):52-54.

[62]齐 昕,宁利中,刘嘉夫,等.极小长高比腔体内混合流体Undulation行波对流[J].力学季刊,2013,34(4):253-261.

[63]JungC,LuckeM,BuchelP.Influenceofthrough-flowonlinearpatternformationpropertiesinbinarymixtureconvection[J].Phys.Rev.E,1996,54(2):1 510-1 529.

[64]BuchelP,LuckeM.Influenceofthroughflowonbinaryfluidconvection[J].Phys.Rev.E,2000,61(4):3 793-3 810.

[65]石 峯，宁利中，王 芳，等.矩形腔体中Rayleigh—Benard对流结构的分析[J].西安理工大学学报,2008,24(4):484-489.

[66]李国栋,黄永念.有水平流时双流体混合物对流的时空演变[J].力学进展，2004,34(2):263-269.

[67]李国栋,黄永念.水平流作用下行波对流的成长及周期性重复[J].物理学报，2004,53(11):3 800-3 805.

[68]赵秉新.水平流作用下的混合流体行进波对流[J].水动力学研究与进展，2012,27(3):264-274.

Research progress of Rayleigh-Benard convection in binary fluid mixtures

LI Kai-Ji,NING Li-Zhong*,WANG Na,WANG Yong-Qi,HU Biao

(State Key Laboratory Base of Eco-hydraulic Engineering in Arid Area，Xi’an University of Technology,Xi’an 710048,China)

On the basis of introducing the research methods of the Rayleigh-Benard(RB) convection in binary fluid mixtures,the linear stability analysis,the blinking wave and several research results of traveling wave convection in binary fluid mixtures along the upper branch of convective bifurcation curve with the change of convective parameters are reviewed.The recent research achievements of the influence of lateral flows on RB convection are summarized,the prospects of the RB convection in binary fluid mixtures are presented.

fluid mixtures；Rayleigh-Benard；linear stability；blinking traveling wave；progress

10.13524/j.2095-008x.2015.03.038

2014-11-10;

2015-01-19

国家自然科学基金资助项目(10872164)；陕西省教育厅专项计划项目(09JK643)；陕西省重点学科建设专项资金资助项目

李开继(1987-)，男，甘肃武威人，硕士，研究方向：水力学、对流动力学，E-mail:348285456@qq.com；*通讯作者：宁利中(1961-)，男，陕西西安人，教授，博士，研究方向：对流动力学、高速水力学，E-mail: ninglz@xaut.edu.cn。

O351.2

A

2095-008X(2015)03-0006-11