基于EMD-Hankel-SVD的高速列车万向轴动不平衡检测
丁建明, 王 晗 , 林建辉 , 黄晨光
(1.西南交通大学 牵引动力国家重点实验室,成都 610031;2. 青岛四方机车车辆股份有限公司 高速列车系统集成国家工程实验室,青岛 266111)
基于EMD-Hankel-SVD的高速列车万向轴动不平衡检测
丁建明1, 王 晗2, 林建辉1, 黄晨光1
(1.西南交通大学 牵引动力国家重点实验室,成都 610031;2. 青岛四方机车车辆股份有限公司 高速列车系统集成国家工程实验室,青岛 266111)
针对EMD(Empirical Model Decomposition)存在模式频率混叠带来的频谱杂乱的根本缺陷,提出一种高速列车万向轴动不平衡动态检测的新方法。该方法的核心是:对万向节安装机座的振动信号进行EMD分解得到基本模式分量,应用基本模式分量信号来构造Hankel矩阵,对该矩阵进行奇异值正交化分解,以奇异值关键叠层作为奇异值的选择准则对信号进行重构,应用重构信号的傅里叶谱来检测高速列车万向轴的动不平衡,消除EMD分解模式频率混叠带来频谱杂乱,提高了谱的清晰度,凸显了故障特征。应用万向轴动不平衡试验数据对该方法进行试验验证,结果表明:该方法能够有效检测万向轴动不平衡引起故障特征和万向轴的固有振动特性,与纯EMD方法相比,该方法在谱的清晰度和故障表征力上得到了显著提高。
高速列车;万向轴动不平衡;EMD;Hankel矩阵;SVD;动态检测
转向架是高速列车的核心部件,起到承载、导向、支撑、动力传递的关键作用,直接决定了高速列车的运行品质和运行安全。万向传动轴是动力传递的核心元件,在CRH5型动车组的动力传递结构中,牵引电机采用体悬结构,齿轮箱采用抱轴式结构[1],万向轴既要传递牵引力矩,又要适应复杂的运动关系[2],其工作环境恶劣,同时万向轴为细长结构,其弯曲刚度、扭转刚度都很小[3],这些原因促使车辆在高速运行过程中万向轴极易产生偏心。加之,车辆在长期的运行中,万向节轴的磨损间隙、万向传动轴平衡滑块的松动等也会导致万向传动轴的偏心。偏心使万向传动轴产生动不平衡附加力矩,加剧传动系统的振动、极易快速破坏传动系统的轴承、万向节等动力传递部件,严重者导致动力中断、机破、车毁人亡等重特大事故的发生。为了保障动力的安全传递,开展万向轴动不平衡车载动态检测技术的研究显得十分迫切和必要。
EMD分解十分适合处理非线性、非平稳信号,突破了基于傅里叶分解、小波分解受测不准原理的约束,能够无限提高频率、时间的分辨率,克服了傅里叶变换分析非平稳信号失去物理意义的根本缺陷,克服了小波分解对小波的基函数依赖,是一种自适应的数据分解方法[4-6]。这些优良特性决定了EMD具有广阔的应用前景,已在齿轮箱、轴承、发电机组碰擦、桥梁健康等故障诊断中得到了成功应用[7-9]。
尽管如此,作者应用EMD来提取高速列车万向轴不平衡故障的研究中,发现频谱十分杂乱,很难检测万向轴不平衡引起的故障特征和万向轴的固有振动特征,极易导致误警、虚警。探究其原因,EMD分解同小波分解一样,同样存在相邻分解模式间存在频率重叠混淆的现象。造成同一内禀模态函数IMF的细节信号的频带变宽,相邻内禀模态函数的频率重叠较大,分解得到的内禀模态函数的噪声变大,频率成分复杂,淹没和混淆故障特征和固有振动特征。为了充分发挥EMD在处理非线性、非平稳信号中的独特优势,同时克服EMD分解与经典小波变换一样存在IMF分量之间频带重叠的共有缺陷,将Hankel矩阵、奇异值分解理论引入到EMD分解中,利用不同特性信号的奇异值的分布规律的不同来减少频率重叠效应,突显故障特征和固有振动特征。
为此,为了克服EMD存在模式频率混叠带来的频谱杂乱的根本缺陷,提出一种高速列车万向轴动不平衡动态检测的新方法。该方法的核心是:对万向节安装机座的振动信号进行EMD分解得到基本模式分量,应用基本模式分量信号来构造Hankel矩阵,对该矩阵进行奇异值正交化分解,以奇异值关键叠层作为奇异值的选择准则对信号进行重构,应用重构信号的傅里叶谱来检测高速列车万向轴的动不平衡,消除EMD分解模式频率混叠带来频谱杂乱,提高了谱的清晰度,凸显了故障特征。应用万向轴动不平衡试验数据对该方法进行试验验证。
1 EMD分解及其等效滤波特性分析
1.1 振动信号的EMD分解
经验模式分解是一种新的非平稳信号分析方法,将万向节安装机座振动信号的这种非线性非平稳信号分解为若干个基本模式分量(IMF)和一个余项。基本模式分量必须满足两个基本条件:条件1,在数据列中,数据的极值点数量和过零点数量必须相等或最多相差一个;条件2,任何一点,极大值和极小值的包络的平均值为零。经验模式分解的详细过程如下:
第一步:给定被分解的振动信号x(k),k=1,2,…N,N表示信号的长度。
第二步:计算信号的极大值点xmax(k)和极大值坐标kmax(k),k=1,2,…Nm,Nm表示出去端点外的极大值点的个数。
第三步:采用线性插值外推纠正信号的极大值点的端点效应,修正原理具体如图1的(a)和(b)所示。
对图1中所示的接近端点的极值点进行线性插值,则有过点1和点2的直线方程为
(1)
则图1中点3的纵坐标为
(2)
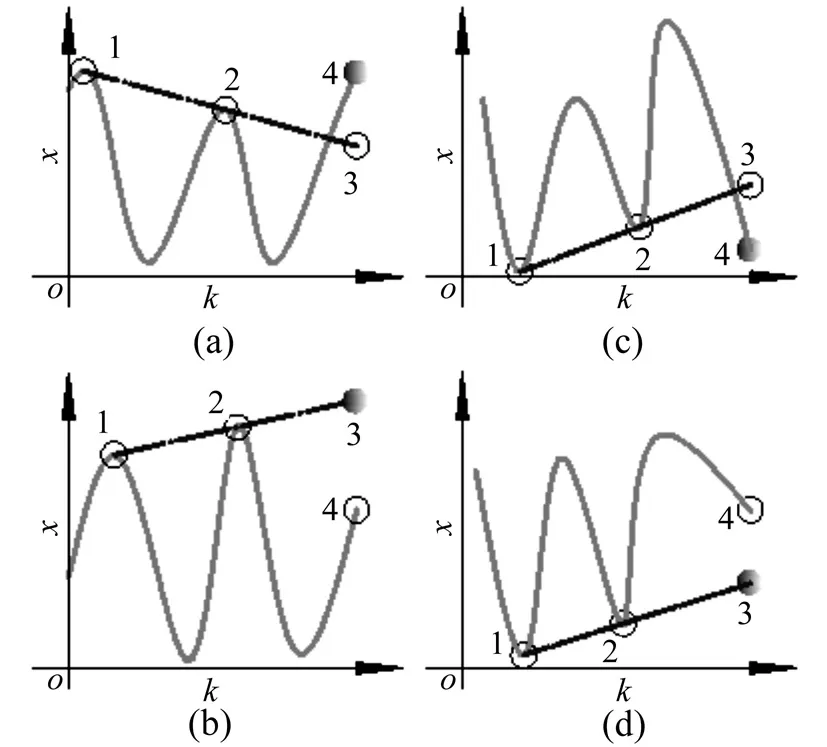
图1 线性插值外推控制端点效应的基本原理Fig.1The basic principle of correcting end effect applying linear interpolation
如果x3≥x4,x3为端点坐标,否则,x4为端点坐标,因此图中红色的点为被选端点,与第二步得到的最大点整合得到包含端点的所有最大极值点。
第四步:计算信号的极小值点xmin(k)和极小值坐标kmin(k),k=1,2,…,Ni,Ni表示出去端点外的极小值点的个数。
第五步:采用线性插值外推纠正信号的极小值点的端点效应,修正原理具体如图1的(c)和(d)所示。同理应用式(1)和(2)来确定x3的值的大小。如果x3≤x4,x3为端点坐标,否则,x4为端点坐标,因此图中红色的点为被选端点,与第四步得到的最小点整合得到包含端点的所有最小极值点。
第六步:采用三次样条对所有极大值点进行插值得到上包络,采用三次样条对所有极小值点进行插值得到下包络,得到上下包络的平均值m1。则有
x(t)-m1=h1
第七步:判断h1是否满足IMF的条件,如果不满足,对h1重复第二步到第六步得到包络的平均值m11,在判断h11=h1-m11是否满足IMF的条件,如不满足则循环s次,使得h1s=h1(s-1)-m1s满足IMF的条件,记c1=h1s,则c1为信号x(t)的第一个满足IMF条件的分量。
第八步:把c1从x(t)中分离出来,得到r1=x(t)-c1,将r1作为原始数据重复第二步到第七步得到信号x(t)的第二个满足IMF条件的分量c2。重复循环n次使得rn为单调函数,得信号x(t)分解为n个满足IMF的分量,则有
(3)
因此,信号分解为n个基本模式分量IMF和一个残余项,则有
1.2 EMD分解的等效滤波特性分析
设定10 000个独立的高斯白噪声数据(其中均值为零,方差为1),对每个高斯白噪声数据应用式(3)进行EMD分解得到不同的IMF分量,计算每个分量的傅里叶频谱,最好计算10 000个信号对应傅里叶谱的平均值并进行幅值归一化,计算结果为EMD的等效滤波特性,具体如图2所示。
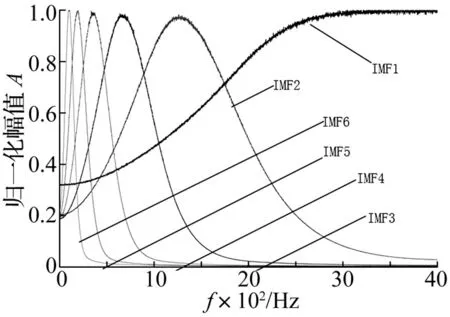
图2 EMD分解的等效滤波特性Fig.2 The equivalent filter characteristics of EMD
从图2中的EMD分解的等效滤波特性可知,EMD分解与小波变换一样,不同IMF之间依然存在频率重叠现象,导致不同的IMF分量信号的噪声变大,分解信号的频率成分更为复杂,频率重叠导致频谱杂乱,混淆和淹没故障特征和固有振动特性。这对万向轴动不平衡的检测、故障判定和故障溯源带来了困难。为了消除这一缺陷,将Hankel矩阵、奇异值变换理论引入到EMD分解中,提出一种融合EMD、Hankel矩阵、SVD的故障检测方法。
2 Hankel矩阵的构造
为了方便应用信号奇异值分解方法,先对EMD分解得到的IMF来构造一个Hankel矩阵,设定近似信号c(i),i=1,3,…Nc,Nc表示信号的长度,利用此信号构造的Hankel矩阵为公式(4)所示[10-11]
(4)
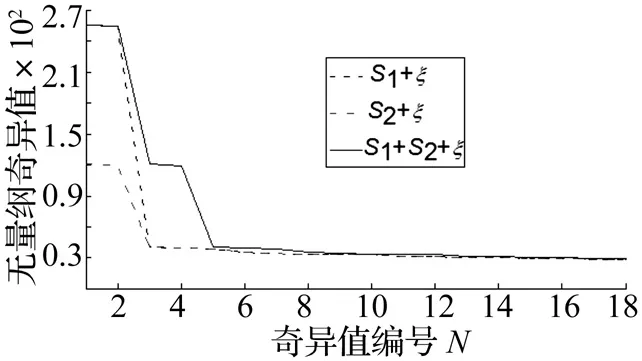
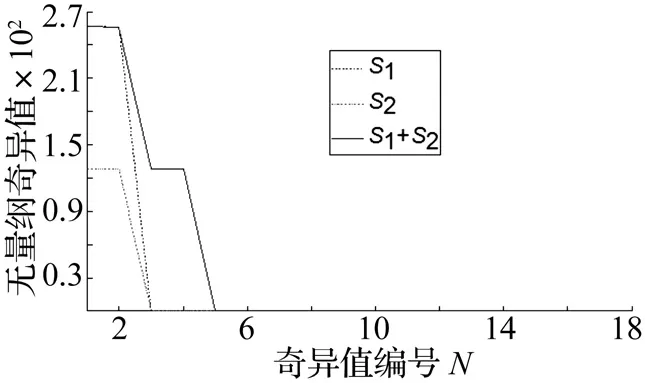
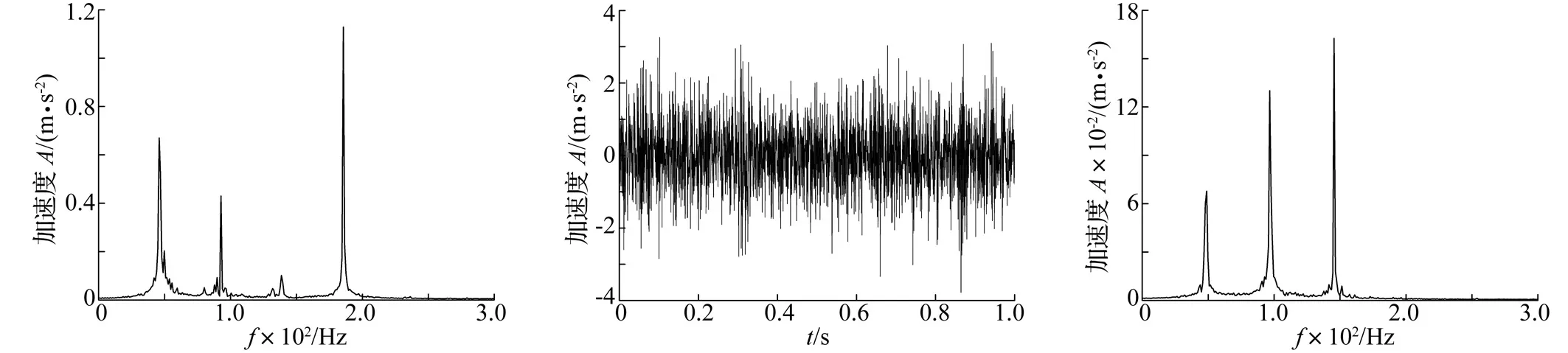
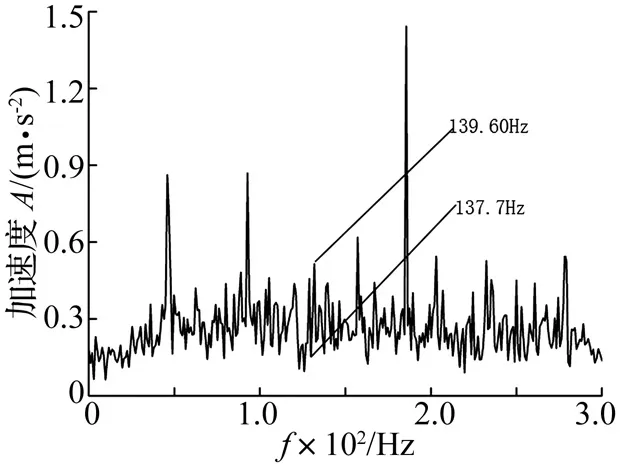
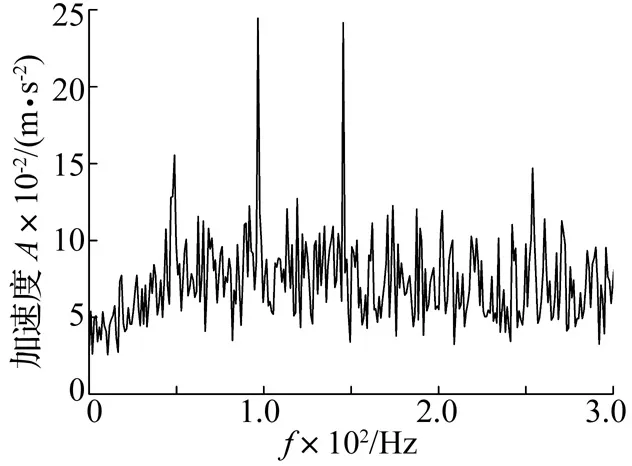
式中:1 3.1 奇异值分解理论 奇异值分解是一种正交化分解方法,对于任意实矩阵A∈Rm×n,无论矩阵行向量或者列向量是否相关,必定存在正交矩阵U∈Rm×m和正交矩阵V∈Rn×n使得 A=UDVT (5) 式中:D=(diag(σ1,σ2,…,σp),0)或者其转置,0表示零矩阵,p=min(n,m),并满足σi≥σi+1 式(5)叫做奇异值分解[10],σi就是分解得到的奇异值。 3.2 奇异值分解对信号的筛选特性分析 假设分解信号IMF由两个部分组成,一是有用信号,二是测量、频率重叠带来的信号噪声 c(i)=s(i)+ξ(i) (6) 则有由c(i)构造的矩阵可以分解为分别由s(i)和ξ(i)构造的Hankel矩阵As和Aξ,即为 Ac=As+Aξ (7) 式中:ξ(i)表示均值为0,方差为1的白噪声 计算式(7)所描述信号的奇异值如图3所示。 图3 含噪声不同频率特性信号的奇异值分布规律Fig.3 Singular value distribution regularity of signal with noise (8) 计算式 (8)所描述信号的奇异值如图4所示。 图4 不含噪声不同频率特性信号的奇异值分布规律Fig.4 Singular value distribution regularity of signal without noise 从图4中可以看出,信号的行相关性大,矩阵呈病态,只有前面几个关键特征值,其余特征值为零,与前面理论分析一致,同时针对不同频率的合成信号的奇异值正好是单一信号的移位组合,这说明不同频率信号具有的奇异值错位特性,奇异值分布规律上呈现叠层结构,这正是消除频率重叠噪声的关键理论基础;从图3中可以看出,噪声的奇异值分布均匀,矩阵呈现良性特性,同时不同频率信号也表现出奇异值的错位特性。为此,本文将EMD与、Hankel矩阵、奇异值理论相结合,利用奇异值对不同频率信号的错位特性来消除EMD分解的频率重叠的缺陷,提高谱的清晰度和对故障的表现力。 依据不平衡故障频率可能存在的范围,对信号进行EMD分解,对单个IMF信构造Hankel矩阵,应用奇异值理论对Hankel矩阵进行奇异值分解,在奇异值的阶梯结构中选择贡献量较大的前3阶奇异值重构信号,用重构信号的傅里叶变换来检测万向轴的动不平衡。检测模型如图5所示。 图5 万向轴动不平衡EMD-Hankel-SVD检测模型Fig.5 The detection model of dynamic imbalance with cardan shaft applying the EMD-Hankel-SVD 从图中5可以看出,万向轴动不平衡检测模型主要包括三个关键步骤:第一步,对振动加速度信号EMD分解得到5个IMF分量;第二步,构造每个分量的Hankel矩阵;第三步,对每个Hankel矩阵进行奇异值分解与重构;第四步,对重构信号做FFT变换,并合并变换信号的频率轴。合并信号的傅里叶谱来检测万向轴的动不平衡。 为了验证本文提出的万向轴动不平衡检测的EMD-Hankel-SVD方法和模型的有效性,搭建了如图6所示的万向轴动不平衡试验台。 图6 万向传动轴动不平衡试验平台Fig.6 Test platform of cardan shaft dynamic unbalance 该试验平台的动力传递途径为:电机、齿轮箱、万向节、万向传动轴、万向节。不平衡轴选用专项修轴(不平衡量超过车辆的使用标准)和新轴(不存在不平衡量)两种。采集万向轴靠近电机端的万向节轴的垂向振动加速度信号作为万向轴不平衡检测的信号源。万向轴的试验转速为2 750 r/min,对存在动不平衡的专修轴做故障试验,采集数据如图7所示。 采用EMD对信号分解得到IMF分量信号分别如图8~图12所示。 “我什么意思你不知道?好吧,让我告诉你,凭我对张仲平的了解,他绝对不会站在你现在站的这个位置上。年轻人,我给你的忠告是这样,人在高处,别两边没有依靠。得防着有人从你背后下手。” 图7 专修轴的不平衡试验数据Fig.7Unbalanceexperimentdataofspecialrevisedshaft图8 IMF1分量信号Fig.8ComponentsignalofIMF1图9 IMF2分量信号Fig.9ComponentsignalofIMF2 图10 IMF3分量信号Fig.10ComponentsignalofIMF3图11 IMF4分量信号Fig.11ComponentsignalofIMF4图12 IMF5分量信号Fig.12ComponentsignalofIMF5 图13 IMF1的SVD分解重构信号Fig.13IMF1reconstructionsignalthroughSVD图14 IMF2的SVD分解重构信号Fig.14IMF2reconstructionsignalthroughSVD图15 IMF3的SVD分解重构信号Fig.15IMF3reconstructionsignalthroughSVD 图16 IMF4的SVD分解重构信号Fig.16 IMF4reconstruction signal through SVD 图17 IMF5的SVD分解重构信号Fig.17 IMF5 reconstruction signal through SVD 分别对信号分量IMF1到信号分量IMF5构造Hankel矩阵,对矩阵进行奇异值分解并进行重构,得到各个分量的重构信号分别如图13~图17所示。 分别对信号IMF1~IMF5的SVD分解重构信号进行傅里叶变换,并合并其频率轴,具体如图18所示。 图18中的关键固有频率结构如表1所示。 表1 专修轴的主要故障频率 结合万向轴的试验转速可知,第1频率45.90 Hz是万向轴的试验转频(2750/60=45.83), 第3频率137.70正好是转频的3倍频。因此通过EMD分解、Hankel矩阵和奇异值分解的万向轴动不平衡检测方法能够有效检测不平衡故障引起的转速基频、倍频等故障特征。为万向轴的不平衡故障检测提供了有效的检测方法。 空心轴的一阶固有频率通用的计算公式得到万向轴的一阶固有频率 (10) 式中:da为万向轴的外径,大小为142 mm;db为万向轴的内径,大小为130 mm;Lc为万向轴长度,大小为1830 mm;η为空心轴系数,取0.8。 则有 f=93.5 Hz 图18中和表1中所示出的第2个频率与万向轴的一阶固有频率十分接近,第2个频率恰好为一阶固有频率的2倍频。因此该方法有效的提取了万向轴的固有振动特性。 在同样的试验条件下,对不存在动不平衡的万向轴新轴做故障试验,采集的试验数据如图19所示。对试验数据进行EMD-Hankel-SVD处理后得到的傅里叶如图20所示(鉴于篇幅,不详细列举EMD、SVD分解的图形)。 图18 专修轴振动数据EMD⁃Hankel⁃SVD处理后的傅里叶谱Fig.18FourierspectrumofEMD⁃Hankel⁃SVDinthespecialrevisedshaft图19 新轴的不平衡试验数据Fig.19Unbalanceexperimentdataofnewcardanshaft图20 新轴振动数据EMD⁃Hankel⁃SVD处理后的傅里叶谱Fig.20FourierspectrumofEMD⁃Hankel⁃SVDinthenewshaft 图20中的关键固有频率结构如表2所示。 表2 新轴的主要故障频率 从表2中可见,没有出现反映万向轴的不平衡带来的故障频率,仅在一阶固有频率附近、0.5倍固有频率附近、1.5倍固有频率附近处出现振动,说明该检测方法虚警几率低,具有较高的可靠性。 直接应用EMD分解得到5个IMF信号分量,对每个分量进行傅里叶变换并合并其频率轴,专修轴数据处理结果如图21所示。 图21 专修轴试验数据纯EMD处理结果Fig.21 Processing of special revised shaft experiment data by EMD 从图21中可以看出,单纯EMD分解模式能够提取万向轴的不平衡振动的基频、一阶固有频率、一阶固有频率的2倍频,原因是EMD本身是一种优良的非平稳信号处理方法。但很难提取出不平衡振动倍频的微弱振动特征,频率点137.7 Hz~139.6 Hz处无能量峰值,是一条直线,原因是微弱特征被频率重叠噪声淹没了。新轴数据处理结果如图22所示。 图22 新轴试验数据纯EMD处理结果Fig.22 The processing of the new shaft experiment data by EMD 从图22中可以看出,单纯EMD分解模式能够提取万向轴的一阶固有频率、0.5倍固有频率、1.5倍固有频率,但是频率杂乱,在轴的旋转频率附近依然存在一定能量的振动,容易误判万向轴的动不平衡故障,造成虚警。 因此与EMD方法相比,EMD-Hankel-SVD检测方法能够提取微弱的不平衡特征,同时谱的清晰度显著提高,除了能够完整提取万向轴的动不平衡的固有特征及其倍频外,也能够提取万向轴承一阶固有频率及其分频、倍频的振动特征,提高诊断的准确性,减少了错误和虚警。 本文将EMD分解、Hankel矩阵、SVD分解相结合,提出一种高速列车万向轴故障检测方法和模型。概括起来具有以下特点: (1) EMD 分解与小波变换相比,是一种自适应的信号分解方法,十分适合处理非平稳信号,但是EMD分解与小波分解一样,同样存在相邻IMF分量的频率重叠混淆的缺陷,易致频率结构混杂,淹没故障特征。 (2) 奇异值分解针对不同频率结构的信号在奇异值分布规律上呈现错位特性,为关键振动模式提取的奇异值选择提供了理论依据。 (3) EMD、Hankel、SVD的有机结合,能够有效提取万向轴动不平衡的基频、倍频的故障特性,同时也能够提取万向轴的一阶固有频率、0.5倍一阶固有频率、1.5倍一阶固有频率的振动特征,基本消去相邻IMF频率重叠对信号特征的混淆和淹没效应。 (4) 该方法与纯EMD相比,其谱的分辨率、清晰度、故障表征力得到了显著提高,对减少虚警漏检、提高故障检测品质具有重要的工程意义。 [1] 冷扬立,李秋泽,李庆国,等. CRH5 型动车组万向轴结构及临界转速分析[J]. 铁道车辆,2010,48(12):6-11. LENG Yang-li,LI Qiu-ze,LI Qing-guo, et al. Analysis of the structure and critical rotating speed of the cardan Shafts for CRH5 multiple units[J]. Railway Vehicles, 2010,48(12):6-11. [2] 张红军,姚远,罗赟,等. CRH5 型动车万向轴传动系统技术特征分析[J].铁道学报,20009,31(2):115-119. ZHANG Hong-jun,YAO Yuan,LUO Yun, et al. Analysis on technical characteristics of CRH5 cardan drive system[J]. Journal of the China Railway Society, 20009,31(2):115-119. [3] 姚远,张红军,罗赟. CRH5型动车万向轴扭转振动分析[J].中国铁道科学,2009,30(2):82-86. YAO Yuan,ZhANG Hong-jun,LUO Yun. Analysis on the torsional vibration of cardan shaft on CRH5 motor Car[J]. China Railway Science,2009,30(2):82-86. [4] Huang N E, Shen Z,Long S et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society London A, 1998, 454( 1971) :903-995. [5] 张超, 陈建军, 徐亚兰. 基于EMD 分解和奇异值差分谱理论的轴承故障诊断方法[J].振动工程学报,2011,24(5):539-545. ZHANG Chao, CHEN Jian-jun, XU Ya-lan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J].Journal of Vibration Engineering,2011,24(5):539-545. [6] Huang N E, WU Zhao-hua,Long S R, et al. On instantaneous frequency[J]. Advance in Adaptive Data Analysis, 2009,1(2):177-229. [7] 时培明,丁雪娟,李庚,等. 一种EMD 改进方法及其在旋转机械故障诊断中的应用[J].振动与冲击,2013,32(4):185-190. SHI Pei-ming, DING Xue-juan, LI Geng, et al. An improved method of EMD and its applications in rotating machinery fault diagnosis[J].Journal of Vibration and Shock,2013,32(4):185-190. [8] Cheng Jun-sheng, Yu De-jie, Yang Yu. The application of energy operator demodulation approach based on EMD in machinery fault diagnosis[J], Mechanical Systems and Signal Processing,2007,21:668-677. [9] Hea X H, Huab X G, Chenb Z Q. EMD-based random decrement technique for modal parameter identification of an existing railway bridge[J]. Engineering Structs, 2011,33:1348-1356. [10] 戈卢布G H,范洛恩 C F. 矩阵计算[M]. 袁亚湘,译.北京:科学出版社,2001. [11] 赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J]. 机械工程报,2010,46(1):100-108. ZHAO Xue-zhi,YE Bang-yan, CHEN Tong-jian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe[J]. Journal of Mechanical Engineering, 2010,46(1):100-108. Detection of dynamic imbalance due to cardan shaft in high-speed train based on EMD-Hankel-SVD method DING Jian-ming1, WANG Han2, LIN Jian-hui1, HUANG Chen-guang1 (1. Southwest Jiaotong University, State Key Laboratory of Traction Power, Chengdu 610031, China;2. CSR Qingdao Sifang Co. Ltd., High-Speed Train System Integration State Engineering Laboratory,Qingdao 266111, China) A new method of detecting dynamic imbalance due to cardan shaft in high-speed train was proposed applying a synthesized method of EMD (Empirical Modal Decomposition), Hankel matrix and SVD (singular value decomposition) against the aliasing defect between adjacent intrinsic model functions existing in EMD. The vibration signals of gimbal installed base were decomposed through EMD to get the different intrinsic model components. The Hankel matrix, constructed of the single decomposition model components, was orthogonally decomposed through SVD and the key singular values were selected to reconstruct the vibration signal on the base of the key stack of singular values. The Fourier spectrum of the reconstructed signal was applied to detect dynamic imbalance of shaft and the clutter spectrum caused by the aliasing defect between adjacent intrinsic model functions was eliminated so as to highlight the failure characteristics. The method was verified by test data in the condition of dynamic imbalance. The results show the method can effectively detect the fault vibration characteristics caused by cardan shaft dynamic imbalance and extract the natural vibration features. By comparison to the simple EMD, the clarity and failure characterization ability are significantly improved. high-speed train; dynamic imbalance due to cardan shaft; EMD; Hankel matrix; SVD; dynamic detection 国家自然科学基金(61134002;51305358);863计划(2011AA110501);精密测试技术及仪器国家重点实验室开放课题(PIL1303) 2014-01-08 修改稿收到日期:2014-05-13 丁建明 男,博士,助理研究员,1981年生 U211.5;U270.331.1 A 10.13465/j.cnki.jvs.2015.09.0303 奇异值分解理论及其对信号筛选特性分析
4 万向轴动不平衡EMD-Hankel-SVD检测模型
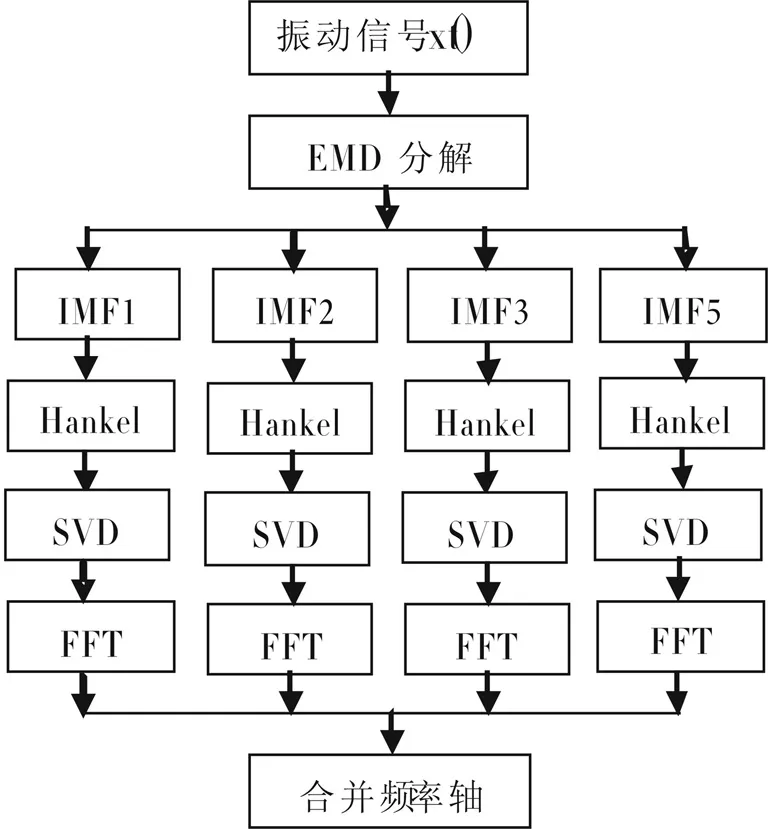
5 万向传动轴动不平衡检测模型的试验验证

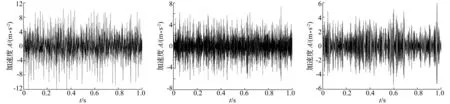




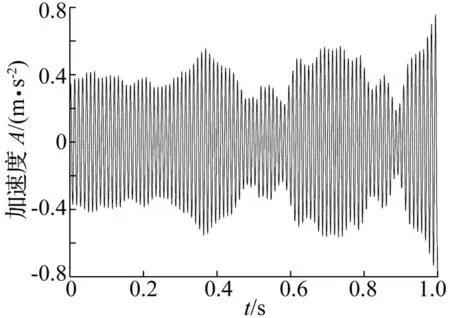
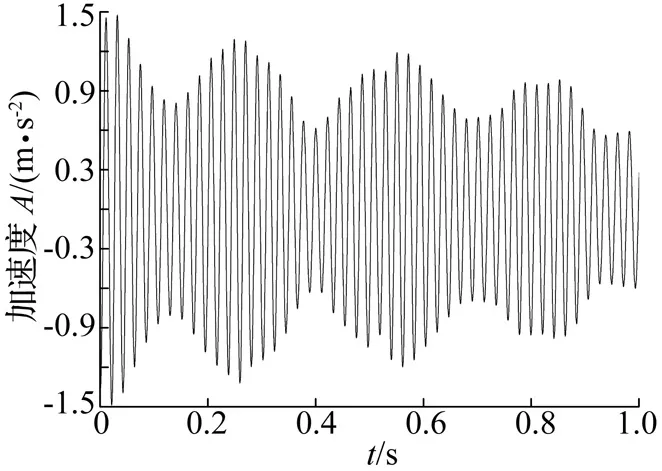



6 与纯EMD方法在万向轴动不平衡检测中的应用比较
7 结 论

