基于EMD和MKD的滚动轴承故障诊断方法

隋文涛 ， 张 丹， Wilson Wang

(1. 山东理工大学 机械工程学院，山东 淄博 255049；山东理工大学 电气与电子工程学院，山东 淄博 255049；3. 加拿大湖首大学 机械工程系，桑德贝 P7B 5E1)

基于EMD和MKD的滚动轴承故障诊断方法

隋文涛1， 张 丹2， Wilson Wang3

(1. 山东理工大学 机械工程学院，山东 淄博 255049；山东理工大学 电气与电子工程学院，山东 淄博 255049；3. 加拿大湖首大学 机械工程系，桑德贝 P7B 5E1)

针对滚动轴承早期微弱故障特征难以提取的问题，提出基于经验模态分解(Empirical Mode Decomposition，EMD)与最大峭度解卷积(Maximum Kurtosis Deconvolution, MKD)的滚动轴承故障特征提取方法。利用EMD方法分解振动信号得到一组固有模态分量(Intrinsic Mode Function，IMF)，然后根据时域峭度和包络谱峭度，筛选出敏感IMF分量进行信号重构。然后对重构信号进行最大峭度解卷积处理以增强故障信息，最后得到包络功率谱，从而获得轴承故障特征频率信息。通过实验台信号验证了所述方法的有效性及优点。

经验模态分解；最大峭度解卷积；故障诊断；滚动轴承

滚动轴承是旋转机械中常用的部件，超过50%的旋转机械故障与轴承故障有关。可靠的轴承故障检测技术有助于在早期阶段识别轴承故障[1]，从而防止机械设备性能退化和提高生产质量。

轴承故障诊断的关键是通过适当的信号处理技术来提取代表性的故障特征。这些技术主要分为时域、频域和时频域。时域分析主要是利用一些统计指标，如峰度和峭度，对设备进行监控。如果监测指标超过了预定的阈值，则认为有故障。时域法的缺点是很难建立适当的阈值，特别是在变工况下。频域分析一般是检查故障特征频率信息，包括一些后处理分析来增强故障信息。例如，双谱、倒谱、频率滤波和包络分析等。然而，经典的频域技术不适合处理非平稳故障信号。非稳态或瞬态特征可以利用时频分析技术如短时傅里叶变换，维格纳分布和小波变换。

经验模式分解(EMD)是一种时频分析工具，它是一种自适应信号分解方法，能够处理复杂的非线性、非平稳信号，突显信号的局部特征，具有良好的时频聚集能力，因此被广泛用于机械信号处理与故障诊断。文献[2]利用经验模式分解和包络谱分析进行液压泵故障诊断，文献[3]运用EMD降噪和谱峭度法对滚动轴承进行早期故障诊断，文献[4]采用EMD与滑动峰态算法提取了滚动轴承故障特征，文献[5]利用EMD和IMF选取算法对转子早期碰摩故障进行诊断。

以上研究展示了EMD在机械故障诊断中的优势，然而EMD同时具有不足之处。在故障诊断中，通常只有部分IMF对故障敏感，能反映故障特征，而其他IMF代表的是干扰成分或者噪声。文献[2-5]在选取IMF方面，只考虑了原信号和IMF在时域内的信息，没有考虑包络谱信息，毕竟包络谱和故障特征频率直接相关。

另外，对于早期微弱故障，选取的IMF还不足以判明故障，还需要有后续处理，继续增强故障信息。

为解决上述问题，本文提出基于EMD和最大峭度解卷积算法的滚动轴承故障特征提取方法。该方法先依据原信号和IMF分量的时域峭度和包络谱峭度剔除EMD分解结果中的虚假分量，再利用最大峭度解卷积算法对IMF进行信息增强，最后经包络解调分析完成故障诊断。将该方法用于滚动轴承故障特征提取，成功提取到故障特征信息，通过实际信号进行了验证。

1 EMD与IMF重构

EMD将非线性非平稳信号分解为一组表征信号特征时间尺度的IMF分量和一个残余项的和[6]。 信号s(t)经EMD分解后可以表示为：

(1)

其中:cm(t)表示第m个IMF分量，rn(t)为第n个残余分量，表示信号的平均趋势。

对振动信号进行EMD分解之后得到了一组IMF，有些IMF是与故障紧密相关的敏感分量，而其他分量与故障无关，甚至是噪声干扰成分。所以在对IMF进行包络功率谱分析之前，需要筛选与故障相关的敏感IMF，以提高故障特征提取精度和故障诊断准确率。

从时域角度看，当某些IMF的峭度值较大时，说明这些IMF中含有较多的冲击成分，即原信号分解后较多的故障冲击成分保留在这些IMF中。信号x(t)的峭度计算公式如下：

(2)

从包络域看，如果能看到明显突出的故障特征频率以及多次谐波，说明这些些IMF含有较多故障信息。简言之，故障信息多的IMF，无论时域还是包络频谱，都应该具有高峭度值。包络公式如下，其中HT表示Hilbert变换。

(3)

基于以上分析，本文提出一种基于包络谱峭度和时域峭度的敏感IMF选择算法。先计算各IMF的时域峭度和包络谱峭度的乘积(indexTE)，选择最大和次大乘积对应的IMF进行重构。indexTE计算公式如下：

indexTE={Kurtosis(x)×
Kurtosis[FFT(env(x))]}

(4)

2 最大峭度解卷积与参数选择

2.1 最大峭度解卷积原理

最大峭度解卷积算法的本质是一个逆滤波器，反作用信号的传递路径，以恢复原始的输入冲击信号。因为最大峭度解卷积滤波器的参数是通过对信号峭度取最大化获得，所以称这种逆滤波器为最大峭度解卷积[7-10]。

图1表达了MKD 解卷积去噪和增强信号的过程。如果滚动轴承有故障，由于内外圈和滚动体之间相互接触，在故障处就会产生冲击性信号s(t) 。s(t)沿着滚动轴承和相关机械部件传递到测量传感器处。传递路径起到对信号的阻抗作用，可由滤波器h来表示。同时，冲击信号也会被混入其它噪声信号n(t)。假设传感器测量得到信号d(t)，MKD逆滤波器f的目标就是消除传递路径的影响，恢复出初始输入冲击信号。可以认为经最大峭度解卷积后的信号是一个更加接近于原始轴承冲击信号的信号。

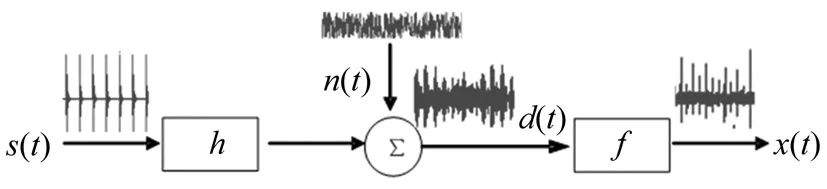
图1 最大峭度解卷积(MKD)过程Fig.1 The process of Maximum Kurtosis Deconvolution

假设输出信号为x(t)，t=1,2,…,N。N是信号的长度。MKD逆滤波器f可以写成有限冲击响应滤波器(长度L)的形式，如下所示：

(5)

为了保证MKD逆滤波器符合因果关系，以下条件需要满足：

f(t)⊗d(t)=δ(t-i)

(6)

其中i是延迟量。

目标函数设为输出信号x(t)的峭度最大化(假设信号已做去均值处理)，如下所示。

(7)

为求最优逆滤波器f系数，使目标函数的一阶导数为零。

∂O(f(j))/∂f(j)=0

(8)

式(8)推导化简后得到：

(9)

其中:b为输入和输出的互相关矩阵，A是输入信号的托普利兹(Toeplitz)自相关矩阵，F就是MKD滤波器的参数。

式(9)写成矩阵的形式：

b=AF

(10)

2.2MKD实现过程与参数选择

MKD实现步骤可以归纳如下：

(1) 计算托普利兹自相关矩阵A；

(2) 初始化MKD滤波器系数F∶F(0)=1；

(3) 根据式(5)计算输出信号；

(11)

其中:I为总迭代计算次数。

(4) 通过式(10)计算b[i]；

(5) 更新F[i]=A-1b[i]；

(6) 计算迭代终止条件：

δ=kurtosis(x[i])-kurtosis(x[i-1])

(12)

将δ与设定值比较，当δ小于设定值迭代终止；否则进入步骤3，开始下一轮迭代循环。

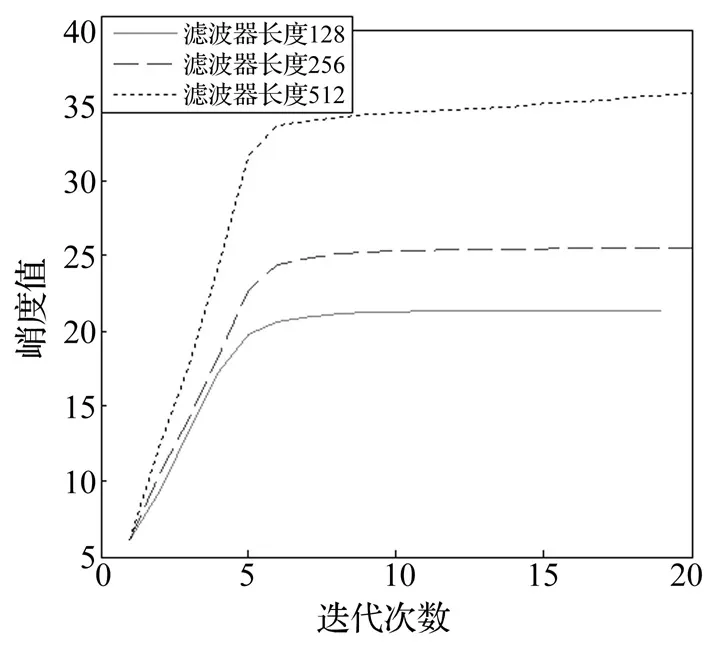
图2 MKD迭代次数与峭度值Fig.2 MKD Iterations and kurtosis values

最大峭度解卷积方法的主要影响因素包括滤波器长度、迭代次数、以及收敛误差。如图2所示，当循环次数大于一定值如20时，MKD输出信号的峭度基本上稳定，尽管增大循环次数可以提高峭度，但是这样做对机械故障诊断而言意义不大。收敛误差一般取0.01。在MKD滤波器设计过程中，影响最大的因素是滤波器长度。因为过长的滤波器长度，会增加计算量，在满足要求的情况下应尽量减少滤波器长度，本文选为512～1 024之间。

3 基于EMD和MKD的轴承微弱故障诊断方法

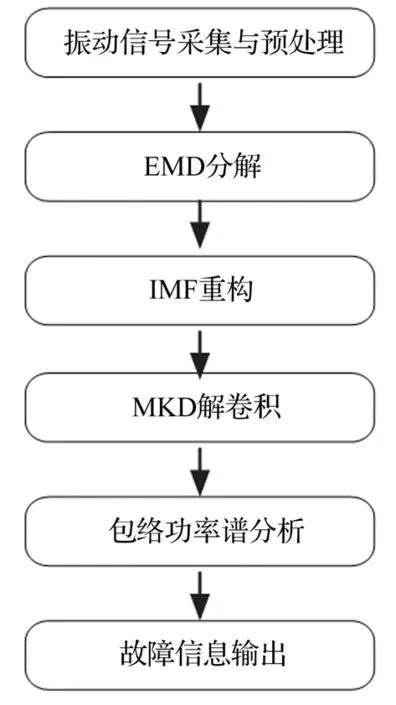
图3 滚动轴承诊断流程图Fig.3 Flowchart of the rolling element bearing diagnosis

虽然EMD方法在轴承故障诊断中取得一定成果，但对其进行最大峭度解卷积(MKD)等后续处理可进一步增强振动信号的冲击特征，有效提取故障信息。 本文提出一种EMD和MKD相结合的滚动轴承早期故障诊断新方法。具体诊断步骤如下，流程如图3所示。

(1) 获取振动信号，进行相应预处理，如降噪。

(2) 对预处理后信号进行EMD分解，然后根据时域峭度和包络谱峭度对IMF分量进行筛选，得到故障特征所在的敏感IMF并重构信号。

(3) 为继续增强重构信号的冲击特征，进行最大峭度解卷积处理。

(4) 计算包络功率谱。因为包络功率谱比包络谱更能突出故障特征成分，抑制频谱中的噪声成分。

(5) 与故障特征频率进行匹配，输出运行信息。

4 实测信号验证

为了验证本文提出方法的有效性和实用性，对滚动轴承试验台上的几种常见的故障进行了试验分析。试验装置和试验数据均来自Wilson.Wang教授的实验室[10]。实验台如图4所示，由感应电机驱动，速度范围为20～4 200 r/min。轴转速可以通过速度控制器(型号：Delta VFD-PU01)进行调节。实验台采用松耦合以消除电机产生的高频振动。滚动轴承装在固定支架上，在测试轴承两个方向上安装加速度传感器。数据采集卡采用NI PCI-4472，采样频率设定在20 480 Hz。

图4 实验台 (1)光编码器 (2)电机 (3)轴承架 (4)智能传感器 (5)径向载荷 (6)平行调节 (7)转子 (8)可调平台 (9)扭矩载荷调整系统 (10)齿轮箱 (11) ICP加速度计 (12)皮带Fig.4 Experimental setup

每个轴承在5个不同转速和3种载荷下进行测试，在每个特定转速和载荷水平下采集204 800个数据。

试验的轴承型号为 MB ER-10K单列深沟球轴承，其主要结构参数如节径、滚动体数目、滚动体直径、接触角等见表1。试验轴承的理论故障特征频率如内圈故障特征频率fi、外圈故障特征频率fo、滚动体故障特征频率fb等见表2。轴承的测试条件见表3。

需要说明的是，表2中的数据表示转轴频率(fr)的倍数，实际的特征故障频率需要该系数与转频相乘才能得到。

表1 试验轴承的主要结构参数

表2 试验轴承理论故障特征频率

表3 试验条件

图5(a)为转速1 500 r/min和载荷2.5 Nm条件下采集的内圈故障振动信号，频谱如图5(b)所示。根据表2计算，理论内圈故障频率为123.75 Hz。原始信号时域峭度为3.481 5。

对内圈故障信号进行EMD分解和IMF重构后得到的信号，如图5(c)所示，峭度值为4.565 9 ，较原信号有所提高。图5(c)信号的频谱为图5(d)，可以看出低频分量得到削弱，中高频分量得以保留，其作用相当于高通滤波，减少了低频干扰的影响。

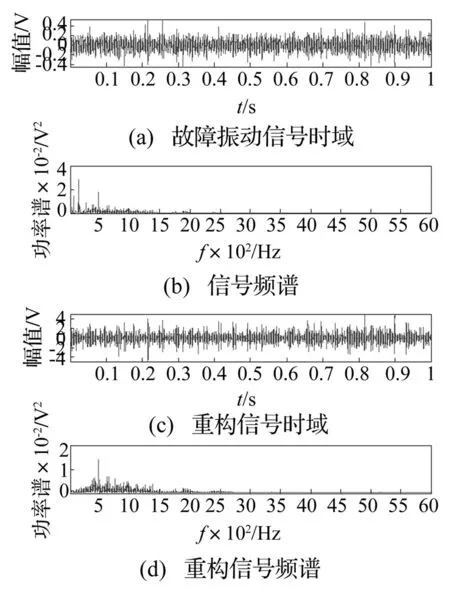
图5 原信号与IMF重构信号时域、频域Fig.5 The waveform and frequency spectrum of the original signal and reconstructed signal with IMF

对图5重构后的信号采用本文提出的解卷积方法分析后，得到时域波形如图6(a)所示，时域峭度为25.345 1，故障冲击信息明显加强。对图6(a)进行包络功率谱分析，得到图6(b)。从中能看到123Hz内圈故障特征频率，以及2、3倍的谐波。同时也可以看到被转频调制的边频成分和转频成分。

相比之下，图6(c)为图5信号的包络功率谱，由于只进行了EMD分解和IMF重构，但是没有后续的解卷积处理，只能看到微弱的1倍故障频率。图6(d)为图4原始信号的包络功率谱，由于没有经过任何处理，没有发现故障信息。

图6 内圈故障分析对比Fig．6 Comparative analysis of roller fault

图7为转速1 500 r/min和载荷2.5 Nm条件下外圈故障振动信号的分析结果，根据表2计算理论故障频率为76 Hz。采用本文提出的方法(简称EMD+MKD)分析后，得到时域波形如图7(a)所示。对图7(a)进行包络功率谱分析，得到图7(b)。从中能看到74 Hz的外圈故障特征频率，以及至少5倍的谐波。

相比之下，图7(c)为进行了EMD分解和IMF重构的包络功率谱，由于没有后续的解卷积处理，能看到明显的2倍故障频率，但是其他倍频处谱峰不明显。图7(d)为图4原始信号的直接包络功率谱，也是只能看到2倍故障频率。

图7 外圈故障分析对比Fig.7 Comparative analysis of outer race fault

为了验证所提出的方法(简称EMD+MKD)的鲁棒性，对Case Western Reserve 大学的轴承滚动体故障振动信号进行分析。滚动轴承的型号为6205-2RS型深沟球轴承，轴承的内径为25 mm，外径为52 mm，厚度为15 mm，节径为39 mm，滚动体直径为7.938 mm，接触角为0°。实验转速1 750 r/min，理论故障频率为137.47 Hz。

图8(a)为原始振动信号，时域峭度为 3.577 2。图8(c)为原始振动信号的包络谱。 对图8(a)采用本文方法分析后，得到时域波形如图8(b)所示，时域峭度为19.327 9 ，故障信息明显加强。对图8(b)进行用包络功率谱分析，如图8(d)所示。从中能看到138.4 Hz 滚动体故障特征频率，以及2～4倍的故障特征频率谐波。

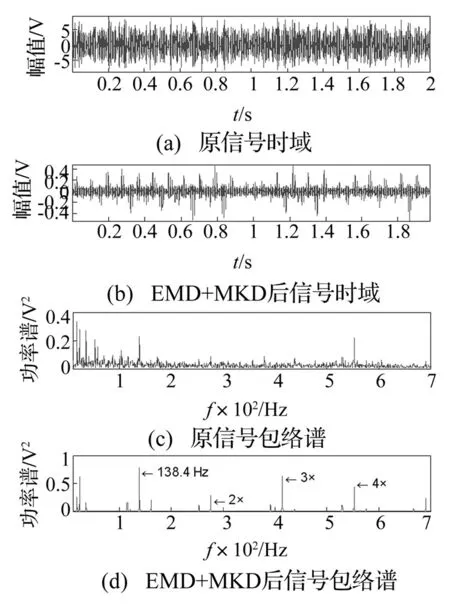
图8 滚动体故障分析对比Fig.8 Comparative analysis of roller fault

5 结 论

(1) 为提取滚动轴承早期微弱故障特征，提出一种结合EMD和MKD的新方法。

(2) 根据包络谱峭度和时域峭度，可剔除传统EMD分解结果中的虚假IMF分量，并将含有故障特征的敏感IMF分量筛选出来。

(3) 通过多个实验信号验证了本文方法提取滚动轴承故障特征比单纯EMD方法和传统包络分析更好，为提取滚动轴承故障特征提供了新的手段。

[1] 周智，朱永生，张优云,等．基于MMSE和谱峭度的滚动轴承故障诊断方法[J]．振动与冲击，2013，32 (6): 73-77. ZHOU Zhi,ZHU Yong-sheng,ZHANG You-yun,et al．Fault diagnosis method for rolling bearings based on MMSE and spectral kurtosis [J]．Journal of Vibration and Shock, 2013,32(6): 73-77.

[2] 唐宏宾，吴运新，滑广军,等．基于EMD包络谱分析的液压泵故障诊断方法[J].振动与冲击，2012，31(9)：44-48． TANG Hong-bin，WU Yun-xin，HUA Guang-jun, et al．Fault diagnosis of pump using EMD and envelope spectrum analysis [J]．Journal of Vibration and Shock, 2012，31(9)：44-48.

[3] 苏文胜，王奉涛，张志新,等．EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击，2010，29(3)：18-21． SU Wen-sheng, WANG Feng-tao,ZHANG Zhi-in．Application of EMD Denoising and spectral kurtosis in fault early diagnosis of rolling element bearing [J]．Journal of Vibration and Shock, 2010，29(3)：18-21.

[4] 张志刚，石晓辉，陈哲明，等．基于改进EMD与滑动峰态算法的滚动轴承故障特征提取[J].振动与冲击，2012，31(22)：80-83． ZHANG Zhi-gang，SHI Xiao-hui，CHEN Zhe-ming，et al．Fault feature extraction of rolling element bearing based on improved EMD and sliding kurtosis algorithm[J]．Journal of Vibration and Shock, 2012，31(22)：80-83.

[5] 雷亚国．基于改进HilbertHuang变换的机械故障诊断[J].机械工程学报，2011，47(5)：71-77. LEI Ya-guo．Machinery fault diagnosis based on improved Hilbert·Huang transform [J]．Journal of Mechanical Engineering, 2011，47(5)：71-77.

[6] Huang N H, Shen Z, Long S R,et al．The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proc.R.Soc. London A,1998, 454:903-995.

[7] Ralph A W．Minimum entropy deconvolution [J]．Geoexploration，1978,16(1)：21-35.

[8] Endo H, Randall R B. Application of a minimum entropy deconvolution filter to enhance Autoregressive model based gear tooth fault detection technique[J]. Mechanical Systems and Signal Processing, 2007,21：906-919.

[9] Sawalhi N, Randall R B, Endo H. The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis [J]. Mechanical Systems and Signal Processing，2007,21：2616-2633.

[10] Wang W, Lee H．An energy kurtosis demodulation technique for signal denoising and bearing fault detection [J]．Measurement Sciences and Technology，2013，24：1-11.

[11] 王宏超，陈进，董广明．基于最小熵解卷积与稀疏分解的滚动轴承微弱故障特征提取[J]. 机械工程学报，2013，49(1)：88-94. WANG Hong-chao, CHEN Jin, DONG, Guang-ming．Fault diagnosis method for rolling bearing’s weak fault based on minimum entropy deconvolution and sparse decomposition [J]．Journal of Mechanical Engineering, 2013，49(1)：88-94.

[12] Loparo K A. Bearings vibration data set, http://csegroups.case.edu/bearingdatacenter/.

Fault diagnosis of rolling element bearings based on EMD and MKD

SUI Wen-tao1, ZHANG Dan2, Wilson Wang3

(1. School of Mechanical Engineering, Shandong University of Technology, Zibo 255049, China；2. School of Electrical & Electronic Engineering, Shandong University of Technology, Zibo 255049, China；3. Dept. of Mechanical Engineering, Lakehead University, Thunder Bay, ON, Canada P7B 5E1,Canada)

Aiming at the difficulty in feature extraction of early faults for rolling element bearings, the method based on Empirical Mode Decomposition (EMD) and Maximum Kurtosis Deconvolution (MKD) was proposed to extract features. The vibration signal was decomposed into a group of Intrinsic Mode Functions (IMF) through EMD. According to the kurtosises of time-domain signal and of envelope spectrum, the sensitive IMF components were selected and reconstructed into a new signal. The reconstructed signal was processed by using MKD to enhance the fault information. Finally, the envelope power spectrum was obtained to analyze the bearing fault characteristic frequency information. The effectiveness and advantages of the proposed method were proved by processing the signals collected from test rig.

empirical mode decomposition; maximum kurtosis deconvolution; fault diagnosis; rolling element bearings

国家自然科学基金(51105236)；山东省自然科学基金 (ZR2012EEL06)

2013-12-05 修改稿收到日期：2014-04-30

隋文涛 男，博士，副教授，1977年生

TP206

A

10.13465/j.cnki.jvs.2015.09.010