基于系统相似方法的叠堆型压电驱动器非线性动力学建模及实验研究

官长斌， 陈 君， 汪旭东， 焦宗夏

(1.北京控制工程研究所，北京 100080； 2. 北京航空航天大学 自动化科学与电气工程学院，北京 100191)

基于系统相似方法的叠堆型压电驱动器非线性动力学建模及实验研究

官长斌1， 陈 君1， 汪旭东1， 焦宗夏2

(1.北京控制工程研究所，北京 100080； 2. 北京航空航天大学 自动化科学与电气工程学院，北京 100191)

根据机械系统与电气系统的相似方法，将叠堆型压电驱动器的非线性电-机械耦合模型完全转换到电气域内，建立其非线性相似电路模型；给出了非线性相似电路模型中迟滞因子的辨识方法，并对某款商用叠堆型压电驱动器进行了迟滞因子的辨识试验；基于非线性相似电路模型和迟滞因子的辨识结果，对该款叠堆型压电驱动器的非线性特性进行了仿真分析,得到了其非线性位移迟滞回线；仿真结果与试验结果吻合，证明了该建模过程与辨识方法的正确性。该建模方法在电气域内对叠堆型压电驱动器电-机械耦合特性及非线性迟滞特性进行描述，建模过程物理意义清晰且简单实用，对于研究压电驱动器的动态特性及控制算法具有实际意义。

叠堆型压电驱动器；非线性建模；迟滞因子；系统相似方法

压电驱动器是近些年来得到迅速发展的新型电动驱动器，它利用压电陶瓷的逆压电效应将电能转化为机械能，具有结构紧凑、定位精度高、响应快、输出力大、无电磁干扰等优点，因此被广泛应用于振动主动控制[1]、高频伺服作动系统[2]以及航天器微型冷气推进系统[3]中。然而，其输出位移过小的缺点严重限制了其应用范围。为了获得可用的位移输出，一般需要对压电陶瓷的输出位移进行放大，常用的放大方法包括压电片堆叠、单晶片或双晶片结构[4-6]。其中，堆叠型压电驱动器具有更好的力学特性和动态特性，并且便于与放大机构联合使用，成为目前最有效、最实用的压电驱动器形式。

叠堆型压电驱动器不但是一种典型的电-机械耦合系统，而且具有明显的非线性迟滞特性。在早期的压电驱动器建模研究中，为了简化建模过程，大都忽略其非线性,只是线性化地研究了压电驱动器的电-机械能量转换过程。此类模型包括静态模型、动力有限元模型和动力阻抗模型[7]，但是以上三种模型均为纯力学模型,对于考察压电驱动器的电学特性具有明显的不足。为了克服这一缺点，文献[8]利用相似系统思想，建立了压电驱动器的相似电路耦合模型，使得系统建模过程物理意义更加清晰，但是该模型同样没有考虑压电驱动器的非线性迟滞特性。

随着对压电驱动器定位精度要求的提高，人们期望通过研究压电驱动器的非线性迟滞特性，为压电驱动器的控制算法提供更多的理论支撑，因此各国研究人员在分析其非线性迟滞特性成因的基础上，提出了多种建模方法。比较典型的有Preisach模型[9]、Duhem模[10]、Maxwell滑动模型[11]以及Prandtle-Ishlinskii模型[12]。上述模型中所包括的参数一般都比较多，这给非线性模型的建立或辨识带来了不便。为了能够更加方便地描述压电驱动器的非线性迟滞效应，Adriaens等[13]提出了一个只包含三个参数的一阶微分方程，用它来描述这种非线性迟滞现象，并且给出了方程中三个参数的辨识方法。虽然文献[9-13]给出了压电驱动器非线性迟滞特性的不同表达形式，但是在电-机械耦合特性的理论分析方面，都是将压电驱动器分解到两个物理域内(电气域和力学域)进行模型的建立，这种建模方式物理意义不清晰，无法直观地理解压电驱动器的能量传递过程。

本文根据系统相似方法，将叠堆型压电驱动器的非线性电-机械耦合模型完全转换到电气域内，建立了其非线性相似电路模型；阐述了叠堆型压电驱动器迟滞因子的辨识方法，并对某款商用叠堆型压电驱动器进行了迟滞因子的辨识试验；基于动态仿真框图和辨识的迟滞因子，对叠堆型压电驱动器的非线性特性进行了仿真分析，并与试验结果进行了对比。该建模方法在电气域上揭示了叠堆型压电驱动器的电-机械耦合机理及非线性迟滞特性，使建模过程物理意义清晰，能够直观地理解压电驱动器的能量传递过程。

1 典型叠堆型压电驱动器的结构

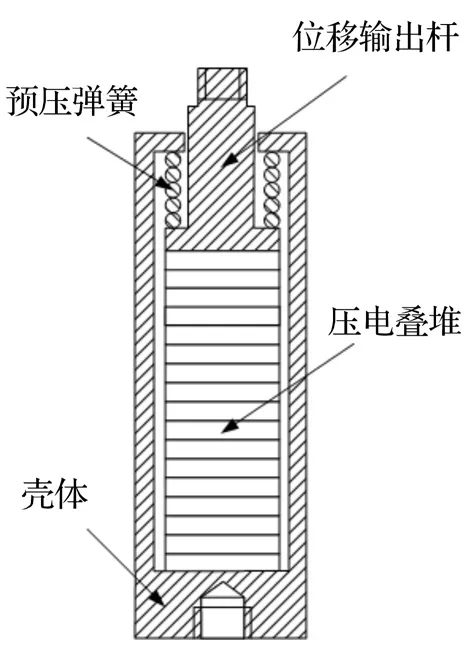
图1 叠堆型压电驱动器的结构示意图Fig.1 Schematic of stack-type piezoelectric actuator

叠堆型压电驱动器由很多压电陶瓷片粘接而成，是一种机械上串联、电气上并联的结构。这种压电驱动器的优点是在低压驱动情况下，能够输出较大的位移和力，同时频率响应快。但是，这种压电驱动器同时具有一个明显的缺点是不能承受拉力，因为拉力会使粘接在一起的压电叠片脱离，进而引起压电驱动器断裂。因此，为了使其在实际应用中具有较好的可靠性，一般是采用预压弹簧给压电叠堆提供一定的预压缩力，这样才能使得压电驱动器能够承受一定的拉力，提高其力学性能。此外，压电叠堆的位移通过一个位移输出杆输出。所以，压电叠堆、预压弹簧和位移输出杆就构成了典型的叠堆型压电驱动器，如图1所示。

2 叠堆型压电驱动器的非线性动力学建模

2.1 非线性相似电路模型

压电材料除了具有迟滞非线性之外，它本身还是一种具有电-机械耦合效应的材料。Goldfarb等[11]给出了一种描述压电叠堆电-机械耦合行为的方法。基于Goldfarb的理论，建立了叠堆型压电驱动器的电-机械耦合模型，如图2所示。

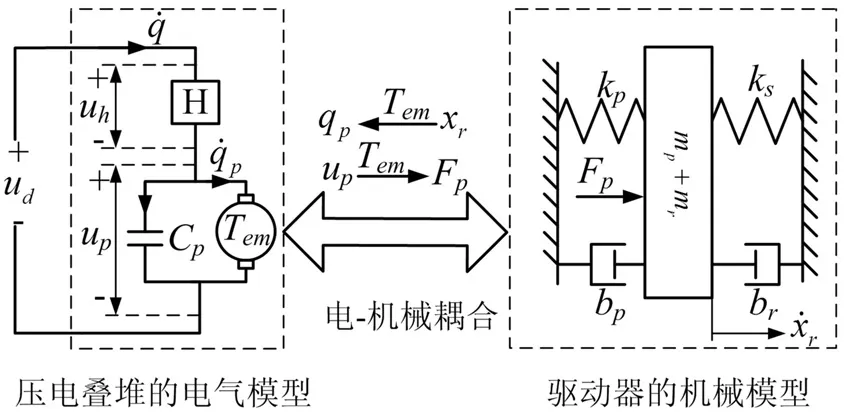
图2 叠堆型压电驱动器的电-机械耦合模型Fig.2 Electromechanical coupling model of stack-type piezoelectric actuator

图2所示的叠堆型压电驱动器的电-机械耦合模型，是在电气和机械两个物理域内对压电驱动器进行了模型的描述。为了使压电驱动器的模型描述过程物理意义清晰，下面利用相似系统思想，将整个压电驱动器都在电气域内进行描述，建立了叠堆型压电驱动器的非线性相似电路模型。

根据线性系统微分方程的相似性，具有不同物理含义的线性系统均具有自己的等效电路模型，这被称作“系统相似方法”[14]。表1给出了机械系统物理量与电气系统物理量的相似性对比。

表1 机械系统与电气系统的相似转换

基于机械系统与电气系统的相似方法，将如图2所示的叠堆型压电驱动器的电-机械耦合模型在电气域内进行描述，得到了如图3所示的叠堆型压电驱动器的非线性相似电路模型。图3完全从电路的角度来解释叠堆型压电驱动器的电-机械耦合特性，使得驱动器机理描述更加清晰，这有利于更加直观地诠释叠堆型压电驱动器的能量流，也能更加方便地建立叠堆型压电驱动器的状态方程。

图3 叠堆型压电驱动器的非线性相似电路模型Fig.3 Nonlinear simulative circuit model of stack-type piezoelectric actuator

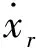
参考图3，可以得到叠堆型压电驱动器的非线性动力学方程：

ud=uh+up

(1)

q=H(uh)

(2)

up=Fp/Tem

(3)

q=qp+Cpup

(4)

qp=Temxr

(5)

(6)

其中:H代表叠堆型压电驱动器的迟滞因子，也是表征压电驱动器非线性的参数。

此外，压电叠堆的等效刚度系数kp可表示为[15]：

kp=EpAp/lp

(7)

其中:Ep为压电叠堆的杨氏模量，Ap为压电叠堆的截面积，lp为压电叠堆的长度。

压电叠堆的质量mp可表示为：

mp=ρpAplp

(8)

其中:ρp为压电叠堆的密度。

电-机械转换系数Tem可由下式表示[15]：

Tem=d33npkp

(9)

其中:d33为压电陶瓷的应变常数，np为压电叠片的数量。

基于式(1)～式(6)的非线性动力学模型，建立了叠堆型压电驱动器的动态框图，如图4所示。该动态框图包含了迟滞非线性、电-机械耦合特性和位移输出杆动特性等因素，直观地解释了叠堆型压电驱动器的工作机理。其中，G(s)是代表位移输出杆动特性的传递函数，它是由式(6)推导而来的，可以表示如下：

(10)

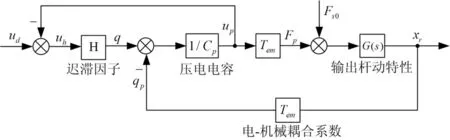
图4 叠堆型压电驱动器的动态框图Fig.4 Dynamic diagram of stack-type piezoelectric actuator

2.2 迟滞因子的辨识方法

迟滞现象是压电材料的一种固有特性，它的存在会影响压电驱动器的性能。很多学者[9-12]都对压电材料的迟滞非线性进行过研究，并提出了很多能够描述这种特性的数学模型。为了能够更加方便地描述压电陶瓷驱动器的迟滞效应，本文采用Adriaens等[13]所提出的一阶微分方程来描述这种现象，并且给出了方程中三个参数的辨识方法。Adriaens所提出的一阶微分方程表示为：

(11)

根据文献[13]，为了辨识式(9)中的三个参数，首先应该得到迟滞现象引起的电压uh和电荷q之间的非线性曲线。但对于叠堆型压电驱动器，uh与q之间的曲线不容易测得，而容易测得的是其位移xr与驱动电压ud之间的非线性迟滞曲线。

下面我们将利用已知的xr与ud之间的迟滞关系推导得到辨识所需要的uh和q之间的迟滞关系。

联立式(3)～(5)，可以得到

(12)

(13)

假设压电驱动器处于空载情况下，则Fp可以表示如下：

Fp=kpxr

(14)

将式(12)代入到式(10)和式(11)中，可得：

(15)

(16)

结合式(15)，式(16)以及(xr,ud)曲线，可以获得uh和q之间的非线性迟滞曲线。

[13]，由(uh,q)迟滞曲线的中心点位置、平均斜率和迟滞曲线面积，可以得到式(11)中的三个参数，表示如下：

(17)

(18)

(19)

其中:qur和qll分别为(uh,q)迟滞曲线的右上端点和左下端点所对应的电量值，qc为(uh,q)迟滞曲线的中心点对应的电量值，A为uh的幅值，ε为迟滞环的面积。

3 叠堆型压电驱动器迟滞因子的辨识实验

本文所使用的叠堆型压电驱动器是德国Physik Instrumente公司的产品，型号是P-843.40，内置应变计传感器(SGS，Strain Gauge Sensor)；高精度的SGS用来测量叠堆型压电驱动器的位移。该叠堆型压电陶瓷驱动器的物理参数列在了表2中。

首先对P-843.40型压电驱动器的准静态性能(位移与驱动电压的关系)进行了测试，测试装置如图5所示。信号发生器产生频率为0.05 Hz、幅值为5 V、偏置5 V的三角波信号(如图6所示)，这个信号通过Physik Instrumente公司压电功率放大器(由E501.00型机箱外壳和E504.00F型功率放大模块组成)放大之后，形成压电驱动器的驱动电压。位移信号通过SGS获得，位移信号和信号发生器产生的三角波信号都通过信号调理箱进入工控机，这两个信号都由工控机中的Advantech PCI1716型A/D板卡采集。经过简单地数据处理之后，就可获得压电陶瓷驱动器的位移xr与其驱动电压ud之间的关系曲线，如图6所示。

表2 P-843.40型压电驱动器的参数

图5 压电驱动器位移测量装置Fig.5 Displacement measuring equipment of stack-type piezoelectric actuator

图6 三角波控制电压Fig. 6 Triangle control voltage

根据式(15)～式(16)以及图7，可以获得迟滞现象引起的电压uh和电荷q之间的非线性曲线，如图8所示。

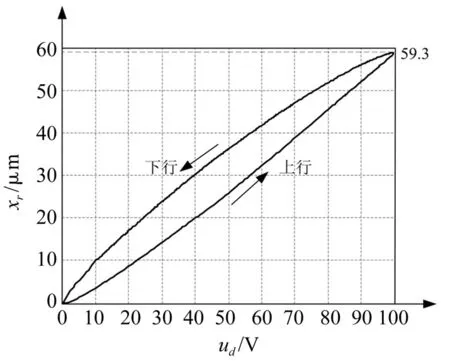
图7 测得的压电驱动器位移与驱动电压的关系曲线Fig.7 Measured relationship between drive voltage and displacement of piezoelectric actuator

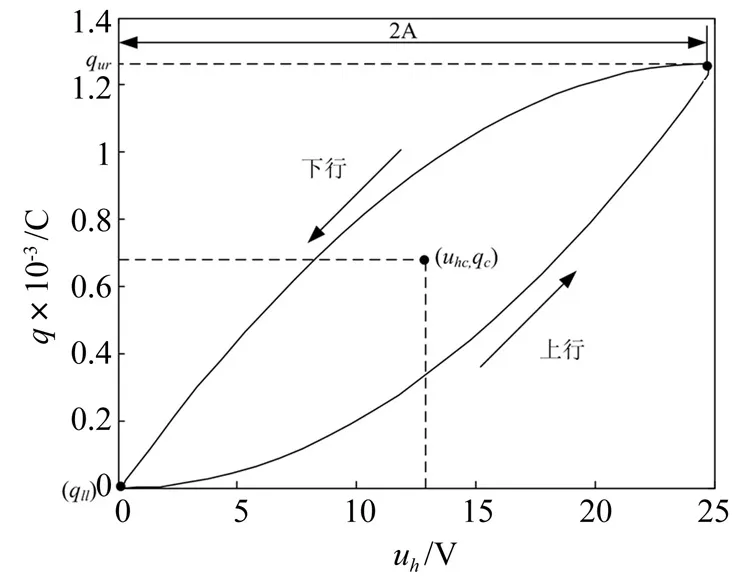
图8 计算得到的(uh, q)迟滞曲线Fig.8 Calculated hysteresis curve between uh and q

式(17)～式(19)方程右侧的参数可以通过图8所示的迟滞曲线得到，这样就得到所要辨识的三个参数(如表3所示)。将辨识参数代入到式(11)中，就得到了本文叠堆型压电驱动器的迟滞因子表达式。

4 仿真分析与结果讨论

在完成了迟滞因子H辨识之后，便可利用如图4所示的叠堆型压电驱动器的动态框图，对其动态特性进行仿真分析。仿真参数见表3。

表3 P-843.40型压电驱动器迟滞因子的辨识参数

为了便于将仿真结果与试验结果进行对比分析，仿真过程中的控制电压同样采用如图6所示的0.05 Hz、幅值为5 V、偏置为5 V的三角波信号。在此驱动电压下，压电驱动器的位移仿真曲线如图9(虚线)所示。同时，利用图5所示的试验装置测得了该压电驱动器在三角波驱动电压下的输出位移，并将其也绘制在了图9中(实线)。从图9可以看出，压电驱动器在三角波指令下的位移输出具有明显的非线性特征，这便是迟滞现象；此外，仿真曲线与试验曲线能够基本的吻合，这就验证了本文所提出的建模方法和辨识方法的正确性。

为了比较压电驱动器迟滞回线的仿真结果和试验结果，将驱动电压ud和输出位移xr之间非线性关系的仿真曲线和试验曲线均绘制在了图10中。通过图10可以看出，仿真与试验测得的迟滞回线能够基本吻合，这再次证明了本文所提出的叠堆型压电驱动器的建模方法和迟滞因子的辨识试验的正确性。

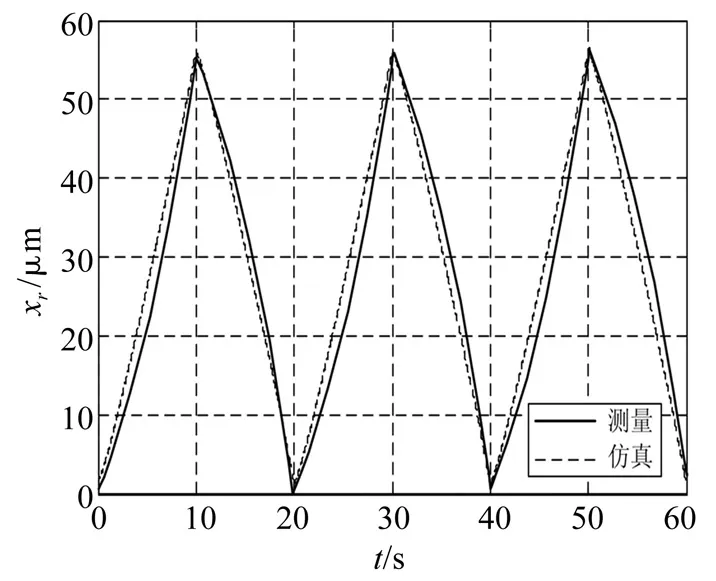
图9 三角波指令下驱动器的位移输出Fig.9 Displacement output under triangle command signal

图10 位移迟滞回线的仿真结果与试验结果对比Fig.10 Comparison between simulated and experimental displacement hysteresis curve

5 结 论

本文根据系统相似方法，通过在电气域内描述电-机械耦合特性和非线性迟滞特性，建立了叠堆型压电驱动器的非线性相似电路模型；通过对某型商用叠堆型压电驱动器的试验研究，验证了该模型的有效性；本文提出的建模方法；具有建模过程简单实用且物理意义明显的优点，对于研究压电驱动器的动态特性和控制算法具有实际意义。

参 考 文 献

[1] Jiao Z, Chen P, Hua Q, et al. Adaptive vibration active control of fluid pressure pulsations [J]. Proceeding of the Institution of Mechanical Engineers, Part I: Journal of System and Control Engineering, 2003, 217: 311-318.

[2] Anderson E H, Evert M E, Flannery P, et al. Image stabilization testbed (ISTAT) [C]. SPIE conference on technologies for synthetic environment: hardware-in-the-loop testing VI, Orlando, FL, 16 April 2001, paper no.4366-24.

[3] Matticari G, Noci G E, Siciliano P. Cold gas micro propulsion prototype for very fine spacecraft attitude/position control [C]. 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Sacramento, USA, 2006:5378-5390.

[4] Chopra I. Review of state of art of smart structures and integrated systerns [J]. AIAA Joumal, 2002, 40(11): 2145-2187.

[5] 吴博达, 鄂世举, 杨志刚, 等. 压电驱动与控制技术的发展与应用 [J]. 机械工程学报, 2003, 39(10):79-85. WU Bo-da, E Shi-ju, YANG Zhi-gang, et al. Development and application of piezoelectric actuation and control [J]. Chinese Journal of Mechanical Engineering, 2003,39(10):79-85.

[6] 赵淳生. 超声电机技术与应用 [M]. 北京: 科学出版社, 2007.

[7] Liang C, Sun F P, Rogers C A. An impedance method for dynamic analysis of active materials systems [J]. Journal of Intelligent Material Systems and Structures, 1997, 8: 718-732.

[8] 李国清, 胡元太, 胡鹏, 等. 相似电路耦合模型及其在压电-梁结构分析中的应用 [J]. 固体力学学报, 1999, 20 (4): 343-348. LI Guo-qing, HU Yuan-tai, HU Peng, et al. A simulative circuit model for intelligent structures and its application to a smart beam with PZT actuator [J]. Acta Mechanica Solida Sinica, 1999, 20 (4): 343-348.

[9] Ge P, Jouaneh M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators [J]. Precision Engineering, 1997, 20(2): 99-111.

[10] Stepanenko Y, Su C Y. Intelligent control of piezoelectric actuators [C]. 37th IEEE Conference on Decision and Control, Victoria University, BC, 1998: 4234-4239.

[11] Goldfarb M, Celanovic N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators [J]. Journal of Dynamic Systems, Measurement, and Control, 1997(119): 478-485.

[12] Schäfer J, Janocha H. Compensation of hysteresis in solid-state actuators [J]. Sensors and Actuators A: Physical, 1995, 49(1): 97-102.

[13] Adriaens H, De Koning W L, Banning R. Modeling piezoelectric actuators [J]. IEEE/ASME Transactions on Mechatronics, 2000, 5(4): 331-341.

[14] Cheng D K. Analysis of linear systems [M]. New Jersey: Addison-Wesley, 1959.

[15] Mayer D, Atzrodt H, Herold S, et al. An approach for the model based monitoring of piezoelectric actuators [J]. Computers & Structures, 2008, 86(3): 314-321.

勘误声明

王世明，刘雨，任顺清. 试验环境条件对离心机稳定性影响分析，2014，33(20)：187-191。该文章内容为作者王世明在哈尔滨工业大学读博期间完成的工作，知识产权归哈尔滨工业大学所有，而不属于天津科技大学，作者本人为此失误负责，同时也对哈尔滨工业大学及振动与冲击杂志社表示歉意。在此声明该文章第一作者单位更改为哈尔滨工业大学。

Nonlinear dynamic modeling and experiment of stack-type piezoelectric actuator based on system similarity method

GUAN Chang-bin1, CHEN Jun1, WANG Xu-dong1, JIAO Zong-xia2

(1. Beijing Institute of Control Engineering, Beijing 100080, China；2. School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China)

According to the method of similarity between mechanical system and electrical system, a nonlinear circuit model of stack-type piezoelectric actuator was established by transforming its electromechanical coupling model to a pure electrical one. The identification method for the hysteresis factor in the nonlinear circuit model was given out and the identification experiments on a commercial stack-type piezoelectric actuator were carried out. Based on the established nonlinear circuit model and the identified hysteresis factor, the nonlinear dynamic characteristics of the piezoelectric actuator were simulated. The simulated hysteresis curve agrees well with the experiment result which verifies the theory. The proposed model can describe the electromechanical coupling characteristics and nonlinear hysteresis characteristics of stack-type piezoelectric actuator in electrical domain with obvious physical sense. The results are of practical significance to study the dynamic characteristics and control algorithm of stack-type piezoelectric actuators.

stack-type piezoelectric actuator; nonlinear modeling; hysteresis factor; system similarity method

民用航天十二五项目

2013-11-01 修改稿收到日期：2014-03-03

官长斌 男，博士，工程师，1984年9月生

陈君 男，高级工程师，硕士生导师，1978年生

TB318

A

10.13465/j.cnki.jvs.2015.09.003