基于AOMP 重建的宽带频谱感知算法

李 琪，赵晓晖

(吉林大学通信工程学院，长春130012)

0 引言

近年来，无线通信业务用户急剧增长，服务要求更为复杂多样，而已授权频段被大量闲置，传统的固定频谱分配方式的有效性面临着挑战。认知无线电技术［1］(CR:Cognitive Radio)是一种能实时感知周围频谱环境，并且能根据不断变化的无线频谱环境进行推理学习，自适应地调整发射机参数(如载波频率，调制方式，发射功率)以利用频谱空洞进行通信的智能无线通信技术［2］。因此，频谱感知是认知无线电系统的核心技术之一。由于窄带频谱感知只在一个窄频带内进行，能发现的频谱机会有限，所以每次扫描多个信道的宽带频谱感知成为新的研究热点。而Nyquist采样定理指出，信号采样速率不得低于信号带宽的两倍，否则，将不能精确地重构原始信号。所以，宽带频谱感知算法的硬件设备面临着巨大的压力，采样率过高、数据量过大成为制约其发展的瓶颈。

压感知理论(CS:Compressed Sensing)融合了信号的采样和压缩编码理论，使采样速率的选取不取决于信号的带宽，而取决于信息在信号中的结构和内容。若信号在某一个正交空间具有稀疏性，就能以远低于奈奎斯特采样频率对其进行采样，并可高概率重构该原始信号［3］。频谱资源利用率低下使宽带信号在频域具有稀疏性，因此，压缩感知理论可应用到宽带频谱感知问题中，Tian等［4］首先应用这一理论，验证了宽带压缩频谱感知(WCSS:Wideband Compressed Spectrum Sensing)的有效性。后来Tian等［5］又提出了一种基于循环特征检测的宽带压缩频谱感知算法，该算法中的二维谱相关函数可直接从压缩测量样本中恢复出来。Zeng等［6］为多跳认知无线电网络提出了一种分布式宽带压缩感知算法，利用空间分集提高检测性能。由于以上算法都要先对宽带模拟信号进行奈奎斯特采样转换为数字信号才能进行压缩测量，为进一步减少数据采集成本，Tropp等［7］设计了一种模拟信息转换器(AIC:Analog－to－Information Converter)，可直接对宽带模拟信号进行压缩测量，将压缩感知理论拓宽到了信号的模拟域。

压缩感知的关键是如何高效地重构原始信号。目前的信号重构算法主要有两大类［8］:一类是凸优化算法，它将l0范数最小化问题转换成l1范数最小化问题，然后利用线性规划求解信号的重构，在这类方法中主要有基追踪法、梯度投影法和内点法等，这类算法精度高，但是计算复杂度大、速度慢;另一类是局部最优化的贪婪迭代算法，这类算法解决低维的最小二乘逼近问题，包括匹配追踪法(MP:Matching Pursuit)、正交匹配追踪法(OMP:Orthogonal Matching Pursuit)等，相对凸优化算法，这类算法的运算量小、速度快，更适用于对实时性要求较高的频谱感知问题。其中OMP算法在已知信号稀疏度的前提下逐渐估计识别信号的支撑集以实现重构，得到了最广泛的应用。但在实际频谱环境中，由于授权用户活动的动态性以及信道的时变性，信号的稀疏度是很难获得的。在未知稀疏度的情况下，无法确定贪婪算法的迭代次数，过早或过晚地终止迭代都会影响算法的重构精度。

基于以上问题，笔者提出了一种AOMP(Adptive Orthogonal Matching Pursuit)重构算法。该算法不需要信号稀疏度作先验知识，先以最大稀疏度为迭代次数，每次迭代通过额外增加的观测样本估算重构信号与原信号的误差，然后找到该误差的最小值点所对应的迭代次数，输出该次迭代重构的信号。仿真结果表明，该算法在不依赖于信号稀疏度的情况下，能有效重构原始信号。

1 系统模型和问题描述

设宽带认知无线电系统要利用的频带宽度为B，将其均匀划分为P个子信道，授权用户随机占用其中的一部分信道，剩余的信道则处于空闲状态，如图1所示。从图1可以看出，宽带信号频域的稀疏性，有很多频谱空洞可以利用。

在认知用户端进行的宽带压缩频谱感知框架［9］如图2所示。定义x(t)为认知用户端接收到的宽带模拟信号，以奈奎斯特采样速率进行采样得到其离散表达形式构成的向量x=［x(1)，…，x(N)］T，其中N为样本数量。用M×N维的随机测量矩阵Φ对信号x进行压缩采样

其中y是M×1维的观测向量，满足M≫N，是信号从其高维空间向一个低维空间的投影，且每个投影值都包含了原始信号大量的信息。由于M≫N，求解式(1)是一个病态问题，无法从M个测量值直接得出信号x。在宽带认知无线电背景下，频谱的低利用率使信号x在频域具有稀疏性，对其进行离散傅里叶变换

图1 宽带频谱感知模型Fig.1 Model of wideband spectrum sensing

图2 宽带压缩频谱感知框架Fig.2 Frame of wideband compressed spectrum sensing

其中F是N×N维的离散傅里叶变换矩阵，s为信号x的频谱，只有K个非零值(K＜M)，称其稀疏度为K。将式(2)代入式(1)，得

其中Θ是M×N维的观测矩阵，当其满足受限等距特性(RIP:Restricted Isomety Property)准则［10］时，通过求解一个基于l0范数最小化的优化问题即可重构信号频谱s，进而利用式(2)的反变换得到信号

由此得到的解是最优的，但式(4)在数值计算上是不可行的，仍属于NP－Hard问题。对此，压缩感知理论提供了很多方法及应用。一个主要方法是将l0范数最小化问题转换成l1范数最小化问题并利用线性规划求解信号重构。根据文献［11］，l1最小范数在一定条件下和l0最小范数具有等价性。于是式(4)可转换为

解决这类凸优化问题主要有基追踪算法，梯度投影法和内点法等，它们得到的解全局最优且稳定，但算法复杂度很高，速度慢。因此，目前逐渐采用新的快速贪婪迭代算法。贪婪迭代算法是解决该重构问题快速有效的算法，包括匹配追踪法、分段匹配追踪法(StOMP:Stagewise Orthogonal Matching Pursuit)、正则正交匹配追踪法(ROMP:Regularized Orthogonal Matching Pursuit)和正交匹配追踪法等。

2 OMP算法

OMP算法是贪婪迭代算法的典型代表。设Γ=supp(s)={i:s(i)≠0}为信号频谱s的非零系数索引集，即支撑集，算法的主要思路为［9］通过迭代循环逐一识别支撑集Γ，然后在此基础上构建信号频谱s的最小二乘逼近，即

其中ΘΓ是观测矩阵Θ的子矩阵，包含由支撑集Γ内元素索引的列，的伪逆。这样OMP算法将稀疏重构问题转换为迭代二乘估计问题，具体流程如下。

输入观测向量y，观测矩阵Θ，初始化s(0)=0，残差r=y，迭代次数l=1，信号支撑集Γ(0)=Ø。

1)计算残差与观测矩阵每列原子的相关度，将相关度最大的那列原子的索引作为候选支撑点

2)将候选支撑集合并到前次迭代估计的信号支撑集Γ(l)=Λ∪Γ(l－1)中。

4)更新残差r=y－Θs(l)。

5)终止判决:若满足终止条件，继续执行6);否则，令l=l+1转回执行1)。

算法结束。

在实际应用中，OMP算法通常以信号频谱s的稀疏度K为迭代终止条件，即算法迭代K次后自行中断，输出频谱重构。

3 序贯压缩感知

文献［12］指出，在对信号x进行压缩测量时，所需测量值的数目满足M=O(Klog(N/K))，y才能包含x的所有信息。可见，M的确定依赖于信号的稀疏度，在盲稀疏度情况下，过多的测量值会造成资源的浪费，过少的测量值又不能保证高概率地重构出原始信号，确定最优观测次数是关键问题。

德城区建成区分阶段扩展特征见表3．由表3可见，扩张速度最快的是在2005—2010年的6年期间，城市建成区加速扩张，增加了29.24 km2，年均增长4.87 km2，扩展速度远高于20年平均增长水平．从扩展强度来看，强度最大的是在2005—2010年间．在2011—2017年这一阶段，扩展强度虽有所降低，但总体趋势是在持续扩张．数据结果总体表明，建成区面积持续扩展，德州市城市发展水平不断提高．

文献［13］和［14］通过序贯压缩采样解决了这一问题。先用初始观测向量yM进行频谱重构，再额外获取T个样本估算重构误差，如果该误差满足设定的门限值，则终止采样;否则，继续获取下一个T长的观测序列，这时前M+T个样本yM+T重构频谱。最终所获得的测量值的数目为M+nT(n=1，2，…)。设由yM重构得到的频谱为，则由额外观测的T个样本估算的重构误差为

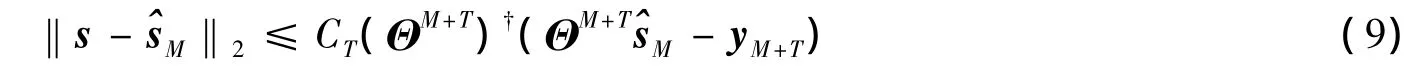
其中(ΘM+T)†=((ΘM+T)HΘM+T))－1(ΘM+T)H。式(9)同样可估计任意次观测所得频谱的重构误差。序贯压缩感知通过逐渐增加额外的样本估算重构误差，从而控制采样过程，确定最优观测次数，减少了能源浪费，笔者借鉴这一思想对OMP算法进行了改进，提出了AOMP算法。

4 自适应OMP算法(AOMP)

4.1 算法分析

由第2节对OMP算法可知，其迭代过程需要以稀疏度为终止条件，在不确定信号频谱s稀疏度的情况下，原OMP算法只能以迭代Kmax次(所利用频谱的最大稀疏度)或剩余残差足够小为终止条件［15］，但会产生过匹配问题，造成很大的重构误差。如图3所示，稀疏度的不确定性导致算法的迭代次数不是最优的，因此重构频谱产生了严重的噪声［15］，其中N为奈奎斯特采样点数。

图3 稀疏度对算法的影响Fig.3 Impact of signal sparsity on the algorithm

由第3节对序贯压缩感知的分析，可将其重构误差估计式(9)应用到OMP算法的迭代过程中，即每次迭代得到的频谱都用额外观测的T个样本进行误差估计，然后在迭代次数范围［Kmin，Kmax］内寻找最小误差对应的迭代次数，该次迭代所得的频谱重构一定是最佳的。该算法最大的优势在于不需要稀疏度作迭代终止条件，而是根据重构误差自适应地选择最优迭代次数，以避免过匹配情况的发生。这种改进后的迭代判决条件很容易应用到其他需要稀疏度作先验知识的贪婪重构算法中，如正则正交匹配追踪(ROMP)算法、子空间追踪(SP:Subspace Pursuit)算法和压缩感知匹配追踪(CoSaMP)算法等。

对于算法需要的最大稀疏度Kmax以及最小稀疏度Kmin，一般情况下，某段频带的稀疏度K虽然未知，但其占用率的范围是容易获得的。如美国NRNRT项目对30 MHz～3 GHz的频谱占用情况做过调查，其平均占用率为5.2% ～13.1%(纽约)，而该频段最小稀疏度 Kmin=N×5.2%，最大稀疏度 Kmax=N ×13.1%

4.2 算法流程

AOMP算法的具体流程如下。

输入初始观测向量yM，初始观测矩阵ΘM、最小稀疏度Kmin和最大稀疏度Kmax。

1)额外观测T个样本，得yM+T，ΘM+T。

3)计算残差与观测矩阵每列原子的相关度，将相关度最大列原子的索引作为候选支撑点Λ=

4)将候选支撑集合并到前次迭代估计的信号支撑集Γ(l)=Λ∪Γ(l－1)中。

6)更新残差r=yM－ΘMs(l)。

7)估计重构误差 e(l)=CT(ΘM+T)†(ΘM+Ts(l)－yM+T)。

8)终止判决:若l＞Kmax，继续执行9);否则，令l=l+1转回执行3)。

9)寻找最佳频谱重构对应的迭代次数t=argmlin(e(l))，t∈［Kmin，Kmax］。

算法结束。

在改进算法中，自适应性体现在步骤7)～9)，步骤7)用额外观测的T个样本估计记录该次迭代的重构误差，以便搜索最优迭代次数;因为信号频谱的稀疏度未知，步骤8)判断算法是否迭代了Kmax次，若满足条件，则终止迭代;步骤9)在算法完成迭代后，对迭代次数区间［Kmin，Kmax］进行搜索，寻找最小重构误差对应的迭代次数，以确定最优迭代次数，最后输出该次迭代重构的频谱，已知最小稀疏度Kmin可缩小搜索范围。由于频谱的低利用率使Kmax值不会太大，因此算法迭代Kmax次造成的额外计算量是可以接受的，AOMP算法的复杂度约为O(KmaxMN)。算法搜索到最优迭代次数对信号重构效果的改进是相当可观的，在同等样本数条件下，重构性能远高于OMP算法。

需要注意的是，CT是与额外观测的样本数T有关的正数，由于在该自适应OMP算法中只需要找出最小误差点，为方便起见，取CT=1。

5 仿真实验及结果分析

利用Matlab平台进行仿真实验验证所提出的AOMP算法的有效性。取要利用的频带宽度为B=32 MHz，子信道共分为P=32个，每个子信道的宽度为1 MHz，已知该段频带的平均占用率为5%～15%。以奈奎斯特采样速率采样宽带模拟信号，N=512为离散样本数，则由该段频带的平均占有率计算可取Kmax=80，Kmin=25。此外选取高斯随机矩阵为测量矩阵Φ，压缩测量所得的样本数M/N在0.2 ～0.4之间。定义信噪比

其中，PS为信号强度，PN为噪声强度，并设定被授权用户所占用的信道信噪比在5～40 dB之间。对每个压缩比及信噪比重复进行500次实验。

为说明迭代终止条件对算法的影响，图4给出了OMP算法和AOMP算法的终止指标。取压缩感知测量值M=200，额外观测值T=10。从图4中可以看出，最佳迭代次数应为信号频谱s的稀疏度，即实际误差最小点所对应的迭代次数。对于OMP算法，由于不确定信号频谱的稀疏度，其终止条件为迭代Kmax=80次或取剩余残差足够小。如果迭代Kmax=80次，由图4知，实际迭代次数大于最佳迭代次数，会发生过匹配情况，最终结果重构误差较大。此外，整个迭代过程残差都是不断减小的，故以剩余残差足够小为终止条件也会导致迭代次数超过最优迭代次数，进而造成算法的过匹配。虽然自适应OMP算法的终止条件也是Kmax=80次，但其记录了迭代过程中的重构误差变化，从图4中可以看出，在两种信噪比下，估计误差最小点都与实际误差最小点相吻合。因此，能准确地找到最优迭代次数，并输出相应的最佳频谱重构。

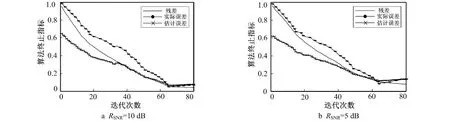
图4 OMP与AOMP算法的终止指标Fig.4 Algorithm termination metrics of OMP and AOMP

图5给出了OMP算法和AOMP算法的实际重构性能。AOMP算法取压缩感知测量值M=200，额外观测值T=10，OMP算法的压缩感知样本数为M+T，授权用户随机占用4个子信道，信道中信噪比为RSNR=5 dB，其他子信道处于空闲状态。图5中横坐标为宽带频谱范围，纵坐标为频谱的幅度值。图5a为原始频谱;图5b为频谱的最佳逼近，即取压缩感知测量值M=512，迭代次数为信号频谱s的稀疏度K时重构的频谱;图5c为OMP算法重构的频谱，由于存在过匹配的情况，重构的有频谱部分几乎淹没在噪声分量中，重构误差较大;而图5d为AOMP算法重构的频谱，它接近于最佳逼近。这是由于该算法通过迭代过程中记录的重构误差变化找出了最优迭代次数，效果相当于算法间接循环迭代了K(稀疏度)次，在压缩样本数相同的情况下，其性能远远高于OMP算法。可见，基于AOMP算法的宽带频谱检测具有良好的实际应用效果。

图5 OMP与AOMP算法的重构性能Fig.5 Recovery performance of OMP and AOMP

图6给出了OMP算法和AOMP算法相对重构误差与CS压缩比的关系。取额外观测值T=10，信道中信噪比为RSNR=10 dB。由图6可以看出，随着压缩比的增加，两种算法的相对重构误差越来越小，但AOMP算法的重构精度要高于OMP算法，这个结果验证了其有效性。此外，AOMP算法在迭代次数上有所改进，故与OMP算法都在压缩比大于0.3后有较好的重构效果。

图7给出了OMP算法和AOMP算法相对重构误差与信噪比的关系。AOMP算法取压缩感知测量值M=200，额外观测值T=10，OMP算法的压缩感知样本数为M+T。由图7可以看出，随着信噪比的增加，AOMP算法的重构精度比OMP算法提升的速度快，并且信噪比越低AOMP算法的优势越明显，这说明AOMP算法具有更好的抗噪声性能，更适用于低信噪比下的压缩频谱感知。信噪比大于40 dB后，两种算法的相对重构误差曲线接近于重合。

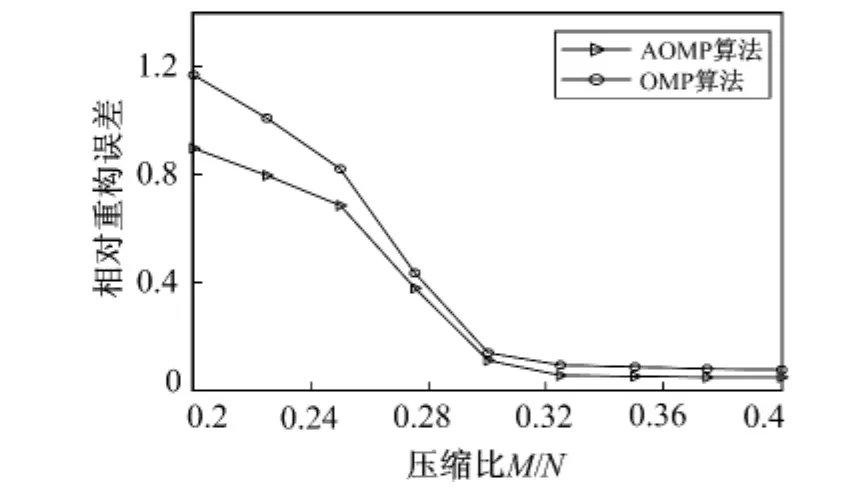
图6 算法重构误差与压缩比关系曲线Fig.6 Estimation errors versus compression rate

图7 算法重构误差与信噪比关系曲线Fig.7 Estimation errors versus SNR

6 结 语

由于在实际频谱环境中，信号的稀疏度很难获得，传统的OMP算法无法进行有效的频谱重构。为此，笔者提出一种基于AOMP的重构算法。仿真结果表明，通过增加额外的观测样本估计迭代过程中的重构误差，可以准确地找到最佳迭代次数进而得到最佳频谱重构。与传统的OMP算法相比，笔者提出的AOMP算法具有更好的重构性能以及抗噪声性能，对于低信噪比下的频谱感知有重要的实际意义。

［1］MITOLA J.Cognitive Radio:An Integrated Agent Architecture for Software Defined Radio［D］.Sweden:KTH Royal Institute of Technology Stockholm，2000.

［2］HAYKIN S.Cognitive Radio:Brain－Empowered Wireless Communications ［J］.IEEE Journal on Selected Areas in Communications，2005，23(2):201－220.

［3］DONHO D L.Compressed Sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289－1306.

［4］TIAN Z，GIANNAKIS G B.Compressed Sensing for Wideband Cognitive Radio［C］∥Proceedings of IEEE International Conference on Acoustics，Speech and Signal Processing.［S.l.］:IEEE，2007:1357－1360.

［5］TIAN Z，TAFESSE Y，SADLER B M.Cyclic Feature Detection with Sub－Nyquist Sampling for Wideband Spectrum Sensing［J］.Selected Topics in Signal Processing，2012，6(1):58－69.

［6］ZENG F，LI C，TIAN Z.Distributed Compressive Spectrum Sensing in Cooperative Multihop Cognitive Networks［J］.Selected Topics in Signal Processing，2011，5(1):37－48.

［7］TROPP J A，LSAKA J N，DUARTE M F，et al.Beyond Nyquist:Efficient Sampling of Sparse Bandlimited Signals［J］.IEEE Transactions on Information Theory，2010，56(1):520－544.

［8］薛男，凌霖，陶晓洋，等.基于压缩感知的信号重构［J］.电子设计工程，2013，21(7):34－36.

XUE Nan，LING Lin，TAO Xiaoyang，et al.Signal Reconstruction Based on Compressed Sensing ［J］.Electronic Design Engineering，2013，21(7):34－36.

［9］吴宏林.压缩感知在认知无线电宽带频谱感知中的应用研究［D］.武汉:华中科技大学电子信息与通信学院，2012.

WU Honglin.Applied Research on Compressive Sensing for Wideband Spectrum Sensing［D］.Wuhan:School of Electronic Information and Communications，Huazhong University of Science＆ Technology，2012.

［10］CANDESE J，ROMBERG J，TAO T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information ［J］.IEEE Transactions on Information Theory，2006，52(4):489－509.

［11］MADNA M.A Systems Perspective on Compressed Sensing and Its Use in Reconstructing Sparse Networks［J］.IEEE System Journal，2014，8(1):23－27.

［12］BLUMENSATH T.Compressed Sensing with Nonlinear Observations and Related Nonlinear Optimization Problems［J］.IEEE Transactions on Information Theory，2013，59(6):3466－3474.

［13］MALIOUTOV D M，SANGHAVI S R，WILLSKY A S.Sequential Compressed Sensing［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4(2):435－444.

［14］顾彬，杨震，胡海峰.基于序贯压缩感知的自适应宽带频谱检测［J］.仪器仪表学报，2011，32(6):1272－1277.

GU Bin，YANG Zhen，HU Haifeng.Adaptive Wide－band Spectrum Detection Based on Sequential Compressed Sensing ［J］.Chinese Journal of Scientific Instrument，2011，32(6):1272－1277.

［15］SUN Hongjian，NALLANATHAN A，JIANG J，et al.Compressive Autonomous Sensing(CASe)for Wideband Spectrum Sensing［C］∥Proc IEEE International Conferene on Communications.Ottawa，Canada:Browse Conference Publications，2012:4442－4446.