高强铝合金压弯构件稳定承载力中欧规范对比

翟希梅，孙丽娟，3，赵远征

（1.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），150090哈尔滨；

2.哈尔滨工业大学土木工程学院，150090哈尔滨；3.中国建筑上海设计研究院有限公司，200063上海）

高强铝合金压弯构件稳定承载力中欧规范对比

翟希梅1，2，孙丽娟1，2，3，赵远征1，2

（1.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），150090哈尔滨；

2.哈尔滨工业大学土木工程学院，150090哈尔滨；3.中国建筑上海设计研究院有限公司，200063上海）

为获得高强铝合金压弯构件稳定性能及其承载力，对29根箱型截面与L型截面6082－T6型高强铝合金构件进行偏心受压稳定承载力试验，获得其失稳破坏特征、承载能力及变形性能.在有限元模型获得试验结果验证的基础上，分析了初始缺陷幅值、截面尺寸、正则化长细比、偏心方向及偏心率等参数对构件的稳定承载力影响及其规律.利用试验及有限元稳定承载力影响参数分析结果，对中国《铝合金结构设计规范》和欧洲规范Eurocode9中的相关计算方法进行验证与结果对比，并对中国《铝合金结构设计规范》中L型截面压弯稳定承载力计算方法进行补充.结果表明：本文有限元模型可以精确地预测铝合金偏压构件的稳定承载与变形性能；中国《铝合金结构设计规范》和欧洲规范计算公式可以用于6082－T6铝合金箱型和L型截面构件压弯构件稳定承载力计算，但都相对保守.

铝合金；压弯构件；数值模拟；屈曲；稳定承载力

铝合金材料具有轻质、高强、耐腐蚀等特点，然而与钢材相比，铝合金弹性模量偏低，承载力受稳定影响比较突出.目前中国铝合金研究主要针对6061－T6型铝合金［1－2］，6082－T6型铝合金基本力学性能与稳定承载力的试验研究才刚开展［3－6］.鉴于中国GB 50429—2007《铝合金结构设计规范》［7］不包括6082－T6型铝合金，并且规范关于压弯构件承载力计算方法因缺少试验数据尚不适用于L型截面构件，因此本文首先进行了13根箱型截面与16根L型截面6082－T6型高强铝合金构件的偏心受压试验研究，同时利用有限元软件ABAQUS对所有偏压试件进行有限元模拟验证，并对影响偏压构件稳定承载力结果的各项影响因素进行稳定承载力参数分析.最后以本文试验与有限元分析结果为依据，对中国《铝合金结构设计规范》和欧洲规范Eurocode9［8］给出的压弯构件稳定承载力计算公式进行验证和对比.

1 压弯构件稳定承载力试验

1.1 试验设计

进行了13根箱型截面与16根L型截面6082－T6型高强铝合金构件在两端铰支情况下的偏心受压试验研究，并以正则化长细比、偏心距e和偏心方向为试验参数进行设计，见表1.采用MTS 2 500 kN电液伺服试验机进行位移加载，见图1.构件上下两端均通过约15 mm厚度的高强石膏固定于带刀铰的钢板槽内，钢板槽与MTS两端对中固定，通过构件在钢板槽内的位置不同，以实现构件的偏心加载.采用位移加载，加载速度为0.005 mm／s，当荷载下降到极限荷载的80%或者变形过大时停止加载.在试件跨中布置位移计和应变片，用来测量构件在加载过程中的变形和应变，测点位置见图2.

表1 构件尺寸及试验结果

1.2 初始缺陷测量

由于6082－T6铝合金试件为挤压成型，其残余应力可忽略不计［9］，故只对试件的初始弯曲采用高精度激光位移计进行测量.初始缺陷测量时，沿构件长度方向每5 cm测量一次，测量构件各截面中心线处的初始缺陷.结果显示：各试件初始缺陷各测点初始缺陷图形基本对称，为正弦半波型；构件初始缺陷幅值基本均不超过构件计算长度的1／1 000，因此本文后续稳定承载力影响参数分析中取Le／1 000作为试件初始缺陷幅值（Le为构件的计算长度，取两端铰支座刀口之间实测距离）.

图1 试验装置

1.3 压弯稳定试验结果与分析

1.3.1 箱型截面试件

试验后所有试件照片见图3，试件承载力及其失稳类型见表1.可以看出对于箱型试件无论绕强轴偏心还是绕弱轴偏心，最终试件均发生绕弱轴弯曲失稳，并且截面宽厚比大（40 mm×80 mm×4 mm和50 mm×100 mm×4 mm）的试件在荷载下降阶段发生整体失稳和局部失稳耦合的现象，而宽厚比较小（40 mm×80 mm×6 mm）的试件只发生整体失稳.不同箱型截面压弯试件绕弱轴方向和绕强轴方向荷载－跨中位移对比见图4.绕弱轴偏心构件在整个加载过程中绕强轴（即沿Y轴）方向位移在±1 mm之间，可以忽略不计，主要发展绕弱轴弯曲变形.绕强轴偏心构件加载初期以绕强轴弯曲变形为主，在荷载下降阶段绕弱轴方向变形不断增大，而绕强轴方向变形增加缓慢.

图2 试件截面形状、应变片与位移计位置示意

1.3.2 L型截面试件

L型截面试件的荷载－跨中位移曲线见图5.由表1和图5可看出：L型截面绕弱轴偏心试件发生绕弱轴平面内失稳，其中小长细比试件荷载偏向肢尖时在荷载下降阶段发生弯扭，荷载－位移曲线末端呈发散状；对于绕弱轴偏心的大长细比试件无论偏心方向正负均发生绕弱轴弯曲失稳，无扭转现象出现，荷载—位移曲线呈“一束”；对于L型截面绕强轴偏心情况，在加载初期均只发生绕强轴弯曲变形，小长细比试件（≤1.0）在接近极限荷载时发生扭转，荷载急速下降，扭转变形发展迅速，卸载后大部分扭转变形恢复；大长细比试件（＞1.0）随着荷载的增加发生绕弱轴弯曲变形，最终绕弱轴弯曲失稳.

图3 试验后试件照片

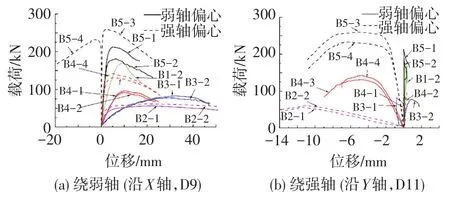
图4 箱型截面试件荷载－跨中位移曲线

图5 L型截面试件荷载－跨中位移曲线

2 有限元数值模拟

2.1 有限元模型建立

本文数值模拟采用的材料本构模型基于Ramberg-Osgood模型［10］，见式（1），参数取值来自同一课题组的拉伸材性试验结果［11］.

式中：E0与f0.2分别为材料的弹性模量与名义屈服强度，E0＝68 133.3 MPa，f0.2＝295.87 MPa；指数n用来描述材料的应变硬化，n＝40.3.

有限元模型中，铝合金构件的单元为S4壳体单元，网格尺寸采用5 mm×5 mm；端板单元采用C3D8R单元，网格尺寸采用10 mm×10 mm.有限元数值模拟时同试验一致，采用位移控制的加载方式.

本文试验现象表明，箱型构件有局部屈曲的现象出现，因此，对箱型截面构件除引入整体弯曲模态形式的初始缺陷外，还引入了局部缺陷，相应的幅值ωd采用Walker公式计算，即

式中：t为构件截面厚度；σcr为弹性屈曲应力，其值可以从有限元特征值屈曲分析得到.

2.2 有限元模型与试验结果对比

有限元最大稳定承载力模拟结果见表1，部分试件的试验与有限元计算结果对比见图6、7.对比结果表明：1）试件最大稳定承载力数值模拟与试验结果误差基本在5%以内，个别L型试件由于截面不规则，试验定位对中难以保证，最大误差达13%；2）有限元模型的破坏过程、失稳形式与试验构件吻合良好；3）加载过程中有限元模型与实测构件测点应变、跨中侧向位移变形基本一致.因此，本文建立的有限元模型可很好预测箱型及L型铝合金压弯构件的稳定承载能力与变形性能.

图6 有限元与试验结果对比

图7 有限元与试验跨中位移和应变对比

2.3 初始缺陷幅值对稳定承载力的影响

对箱型（50 mm×100 mm×4 mm）和L型截面（110 mm×110 mm×10 mm）压弯构件分别进行初始缺陷敏感度分析.初始缺陷幅值分别取构件计算长度的1／500～1／3 000，计算结果见图8.有限元结果表明，构件屈曲荷载随初始缺陷幅值减小而增大，对中等长度构件（1.0≤≤2.0），初始缺陷的影响较大，而对于长构件（＞2.0），初始缺陷的影响较小，可忽略不计，例如L型绕强轴偏心构件当初弯曲幅值ν0由Le／500减小到Le／3 000时，＝1.5与＝2.5时的构件屈曲荷载分别增大11.5%和3%.表明当初始缺陷小于Le／1 000时，构件承载力变化不明显，故稳定承载力参数影响因素分析中采用Le／1 000作为缺陷幅值.

3 稳定承载力影响参数分析

由于试验数据有限，利用可靠的数值模拟方法可进行稳定承载力影响参数分析，以获得不同截面尺寸、正则化长细比，偏心距以及偏向方向下的稳定承载力计算结果，本文共模拟计算了1 890根压弯构件，参数设置见表2.初始缺陷幅值均取为计算长度的1／1 000，初始弯曲均为绕弱轴弯曲.不同偏向方向下相关曲线簇见图9、10，上述图中纵坐标y＝N／(Nyφ)，横坐标 x＝M／M∗，其中 Ny＝f0.2A，M∗＝f0.2Wlx，φ为轴压稳定系数，Wlx为弹性截面模量，图12（c）中φb为受弯构件整体稳定系数.

图8 初始缺陷幅值对稳定承载力的影响

表2 稳定承载力影响参数分析

图9 箱型截面构件相关曲线

图10 L型截面构件相关曲线

4 压弯构件稳定承载力计算方法对比

现行各国规范对于压弯构件稳定承载力的计算分两类，以中国《铝合金结构设计规范》［7］（以下简称《中国规范》）为代表的线性公式，分平面内承载力和平面外承载力计算；以欧洲规范Eurocode9［8］为代表的椭圆线相关公式，分弯曲失稳承载力计算和弯扭失稳承载力计算.

4.1 中国《铝合金结构设计规范》

《中国规范》对于压弯构件承载力计算采用：

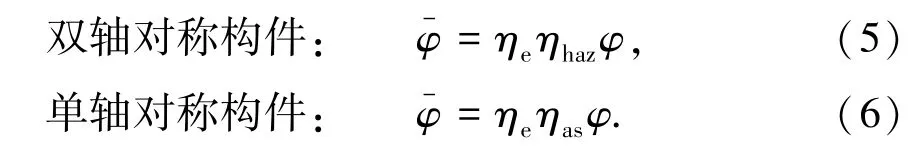
式中：ηe为考虑局部屈曲影响系数，采用有效厚度法考虑局部屈曲影响；ηhaz为焊接缺陷影响系数，本文型材为挤压型材，无焊接，故取ηhaz＝1；ηas为截面不对称系数.

4.1.1 箱型截面压弯构件

由于压弯构件稳定承载力由式（3）、（4）共同控制，只要两公式计算结果不同时高于数值模拟结果即可证明公式是合理适用的.为了验证《中国规范》压弯稳定承载力公式对箱型截面构件的适用性，分别将本文13个（7个绕强轴，6个绕弱轴）箱型截面试验结果和756个（378个绕强轴，378个绕弱轴）有限元箱型截面稳定承载力参数影响因素分析结果代入式（3）、（4）中，对比见图11（y＝N／(Nyφ)）.图11结果表明：全部箱型截面数值模拟结果均没有出现两公式计算承载力高于数值模拟的情况，说明《中国规范》可以用于国产6082－T6箱型截面铝合金压弯构件，但相关曲线族宽，说明《中国规范》公式对于6082－T6铝合金箱型截面压弯构件偏于保守，需要进行合理修正.

图11 箱型截面构件稳定承载力结果

4.1.2 L型截面压弯构件

中国对于单轴对称截面L型压弯构件稳定承载力的试验及理论研究还不充分，仅同济大学郭小农［12］进行了L型截面绕弱轴偏心试验，鉴于上述原因，《中国规范》规定：式（4）仅适用于双轴对称实腹式工字形截面（含H形）和箱型（闭口）截面的压弯构件，且L型截面压弯构件塑性发展系数γx尚无规定.本文参考箱型截面压弯构件式（3）、（4），取γx＝1.0并且不考虑局部屈曲影响，对其中参数η1和η提出建议值，使其适用于6082－T6铝合金L型截面构件.由于L型截面绕弱轴不论正偏心或负偏心情况均发生平面内失稳，故只进行式（3）计算.对于L型截面绕强轴偏心构件，随着长细比的变化均只发生平面外失稳，因此其承载力也只由式（4）控制.

为获得修正后的参数η1，本文首先将378个绕弱轴偏心试件的正则化长细比代入式（7）中，可以得到相应的稳定系数，并在保证与由式（3）计算得到的比值尽可能接近于1.0的前提下对η1进行取值［13］，经计算对于绕弱轴正偏心构件建议取为0.3，绕弱轴负偏心构件建议取为－0.3.η值分别取1.0、0.9、0.8、0.7、0.6、0.5，平面外稳定承载力公式与数值模拟结果对比见图12（c），其中η取0.7与数值模拟结果吻合最好，因此将η取为0.7.图12（a）～（c）为试验、数值模拟与建议公式的比较，建议公式曲线距离试验数据点和数值模拟相关曲线吻合较好，说明对于6082－T6型L型截面压弯构件，本文建议公式能精确预测其稳定承载力.

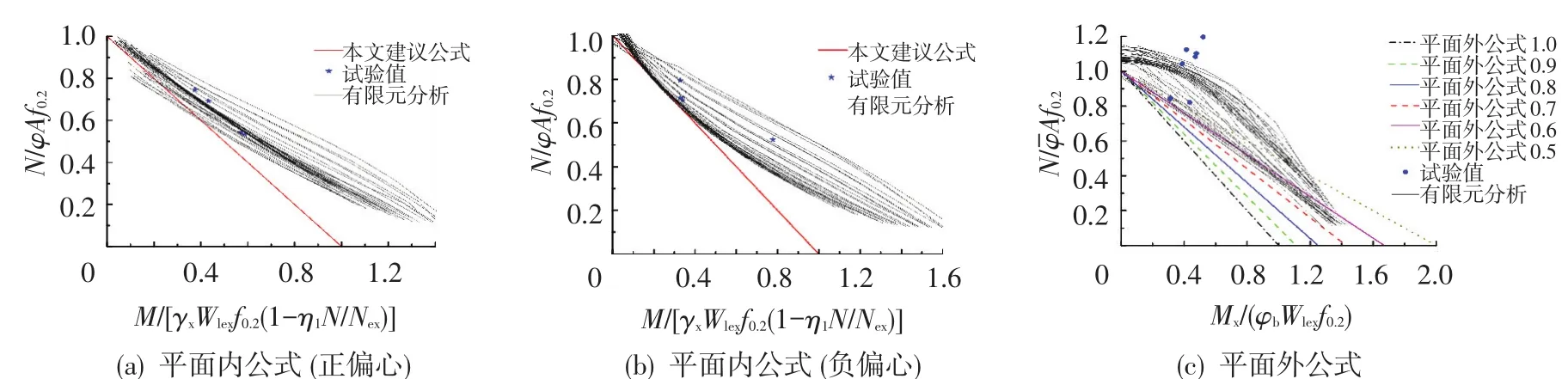
图12 L型截面构件稳定承载力建议公式验证

4.2 欧洲规范Eurocode9

箱型截面弯曲失稳承载力公式为

L型截面弯曲失稳承载力公式为

L型截面弯扭失稳承载力公式为

式中：y代表强轴，z代表弱轴；NEd对应中国规范中的N，MEd对应中国规范中的M；χ与φ物理意义相同，χLT与φb物理意义相同；Mz，Rd和My，Rd分别为受弯构件弱轴和强轴方向承载力设计值，MRd＝αWf0.2／γM1，α相当于中国的γx；NRd为构件轴向受压承载力设计值，NRd＝Af0.2／γM1；ω0、ωx、ωxLT与焊缝有关，本文均取为1.0；ψc、ηc和ξzc可取为0.8，γc取为1.0.Eurocode9对于局部屈曲的影响采用有效厚度法，按受轴力和受弯矩分别确定截面等级分类，分开考虑局部屈曲的影响，采用相关公式来体现组合应力状态，不需要迭代计算.将本文相应试验结果和稳定承载力参数影响因素分析模拟结果代入式（8）～（10）中，见图13～16，大部分数据点均在计算公式上方，说明Eurocode9可以用于国产6082－T6铝合金箱型和L型压弯构件.

图13 箱型截面压弯构件欧洲规范验证

图14 L型截面绕弱轴正偏心欧洲规范验证

图15 L型截面绕弱轴负偏心欧洲规范验证

图16 L型截面绕强轴偏心欧洲规范验证

4.3 两种规范计算结果对比

为将中国规范和欧洲规范Eurocode9进行直观对比，本文做如下统计计算：

中国规范为

Eurocode9（L型）为

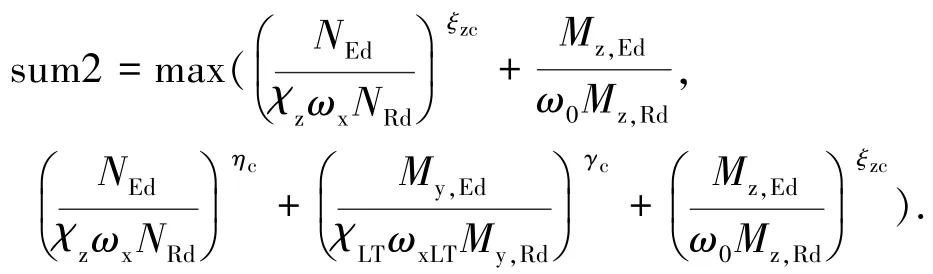
将全部稳定承载力参数影响因素分析结果代入sum1、sum2，计算结果的统计规律见表3.对于箱形截面绕弱轴偏心构件，Eurocode9的均值和变异系数均小于中国规范，说明Eurocode9比中国规范精度更高；对于箱形绕强轴偏心构件，Eurocode9相比中国规范，两者均值和变异系数均相差不大，精度相近，但中国规范压弯构件需计算两个公式，而欧洲规范只需计算一个公式，计算相对简单.

对于L型截面绕弱轴偏心构件，欧洲规范均值偏大，计算结果较保守，而本文建议公式的平均值和变异系数均低于欧洲规范，说明本文建议公式优于欧洲规范；对于L型截面绕强轴偏心构件，本文建议公式相比Eurocode9计算结果精度较好.

表3 中国和欧规范计算方法对比

5 结 论

1）6082－T6铝合金箱型压弯构件均发生绕弱轴整体弯曲失稳，且截面宽厚比大的试件在承载力下降阶段还存在局部屈曲现象.L型截面绕弱轴偏心构件发生绕弱轴的弯曲失稳，部分偏心距为正的小长细比构件在荷载下降段发生弯扭现象；绕强轴构件＜1.0发生弯扭失稳，＞1.0发生绕弱轴弯曲失稳.

2）构件屈曲荷载随初始缺陷幅值减小而增大，当初始缺陷幅值小于Le／1 000时，构件稳定承载力变化不明显.初始缺陷对中等长度构件，即正则化长细比在［1.0，2.0］范围内影响较为明显（最大约12%），而对于长构件（＞2.0），初始缺陷的影响较小，可忽略不计.

3）现行中国《铝合金结构设计规范》规定的压弯构件稳定承载力公式对于6082－T6铝合金箱型构件偏保守.针对6082－T6铝合金L型截面，提出稳定承载力计算方法，即：构件稳定承载力公式形式同式（3）～（4），绕弱轴的偏心构件只进行平面内计算，正偏心时η1取0.3，负偏心时取－0.3；绕强轴偏心构件只进行平面外稳定承载力计算，系数η取0.7.

4）欧洲规范Eurocode9可用于中国6082－T6铝合金压弯构件稳定承载力的计算，对于箱型截面绕弱轴偏心构件，Eurocode9精度高于中国《铝合金结构设计规范》，绕强轴偏心构件，两者精度相当.

［1］郭小农，沈祖炎，李元齐，等.铝合金偏心受压构件理论和试验研究［J］.建筑结构学报，2007，28（6）：136－146.

［2］沈祖炎，郭小农，李元齐.铝合金结构研究现状简述［J］.建筑结构学报，2007，28（6）：100－109.

［3］ZHAIXimei，WANG Yujin，WU Hai，et al.Research on stability of high strength aluminum alloy columns loaded by axial compressive load［J］.Advanced Materials Research，2010，168／169／170：1915－1920.

［4］王誉瑾，范峰，钱宏亮，等.6082－T6高强铝合金材料本构模型试验与理论研究［J］.建筑结构学报，2013，34（6）：113－120.

［5］ZHAIXimei，WU Hai，FAN Feng.Numerical investigation of aluminum alloy column in concentric compression［C］／／Proceedings of 6thInternational Symposium on Steel Structures.Seoul：［s.n.］，2011：738－745.

［6］ZHAIXimei，WU Hai，SUN Lijuan.Stability strength of aluminum alloy columns under concentric compression［C］／／Proceedings of 10thInternational Conference on Advancesin Steel Concrete Composite and Hybrid Structures.Singapore：［s.n.］，2012：60－67.

［7］中华人民共和国住房和城乡建设部.GB50429—2007铝合金结构设计规范［S］.北京：中国建筑工业出版社，2010.

［8］European Committee for Standardization. Eurocode9，BSEN1999－1－1 Design of aluminum structures-General structure rules［S］.Belgium：Brussels，2007.

［9］MAZZOLANIFM.铝合金结构［M］.谭祝梅，译.北京：冶金工业出版社，1992.

［10］RAMBERGW，OSGOODW R.Description of stress-strain curves by three parameters［R］.Washington，D.C.：National Advisory Committee for Aeronautics，TN－902，1943.

［11］王誉瑾，钱宏亮，范峰.结构用铝合金6082－T6材料本构关系及力学参数试验研究［J］.工程力学学报，2013，30（增刊）：309－313.

［12］郭小农.铝合金结构构件理论和试验研究［D］.上海：同济大学，2006.

［13］张铮，张其林.H形截面铝合金压弯构件平面内稳定承载力的试验及理论研究［J］.建筑结构学报，2006，27（5）：9－15.

（编辑赵丽莹）

Com parison of Chinese code and Eurocode9 in calculating the stability bearing capacity of high strength alum inum alloy beam-columns

ZHAIXimei1，2，SUN Lijuan1，2，3，ZHAO Yuanzheng1，2

（1.Key Lab of Structures Dynamic Behavior and Control（Harbin Institute of Technology），Ministry of Education，150090 Harbin，China；2.School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China；
3.China Shanghai Architectural Design and Research Institute，200063 Shanghai，China）

Experimental studies of 29 pin-ended beam-columns，including 13 box-type and 16 L-type sections，extruded from 6082－T6 aluminum alloy，were performed in this paper to investigate the stability behavior and bearing capacity for high strength aluminum alloy.The buckling behavior，stability bearing capacity and deformation performance of all the specimenswere obtained.A finite element（FE）model of aluminum alloy beam-column was conducted by analysis software ABAQUSand verified by experimental results of 29 beam-columns.Initial geometric imperfection which influenced simulation results was analyzed.A parametric study of beam-columns with different cross section dimension，regularized slenderness ratio，eccentric direction and eccentricity ratio，was performed using the FEmodel.Finally，Chinese code and Eurocode9 were verified and compared by the experimental data and the results of the parametric study.Meanwhile the design approach based on Chinese code for L-type cross section beam-columnswas proposed.It can be concluded that the FE model proposed in this paper can well predict the stability bearing capacity and the deformation characteristic for aluminum alloy beam-columns；Chinese code and Eurocode9 can be applied to doubly symmetric box-type cross section and mono-symmetrical L-type cross section beam-columns，but they were both too conservative.

aluminum alloy；eccentric compression；finite element analysis；bucking behavior；stability bearing capacity

TU395

A

0367－6234（2015）12－0001－08

10.11918／j.issn.0367-6234.2015.12.001

2014－08－12.

国家自然科学基金（51108126）.

翟希梅（1971—），女，教授，博士生导师.

翟希梅，xmzhai＠hit.edu.cn.