摩擦摆支座在K 8型单层球面网壳结构中的隔震研究
孔德文,范 峰,支旭东
(1.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),150090哈尔滨;2.哈尔滨工业大学土木工程学院,150090哈尔滨)
摩擦摆支座在K 8型单层球面网壳结构中的隔震研究
孔德文1,2,范 峰1,2,支旭东1,2
(1.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),150090哈尔滨;2.哈尔滨工业大学土木工程学院,150090哈尔滨)
为获得应用摩擦摆支座(FPB)单层球面网壳结构的抗震性能,将摩擦摆支座精细化有限元模型应用到跨度为80 m的K8型单层球面网壳结构中,对两种支承形式的网壳结构施加相同的地震波.依据结构杆件和节点动力响应对摩擦摆支座的隔震效果进行分析,讨论了在水平和竖向地震动时摩擦摆支座的摩擦系数和曲率半径对单层球面网壳地震响应的影响规律.结果表明:随着地震动强度的增强,摩擦摆支座的最优摩擦系数也随之增加;摩擦摆支座曲率半径越大网壳结构的地震响应越小.在上述研究基础上,对单层球面网壳结构如何选择摩擦摆支座进行了一些讨论.
单层球面网壳;摩擦摆支座;隔震;最优摩擦系数;曲率半径
摩擦摆支座(friction pendulum bearing,FPB)由美国加州大学伯克利分校Zayas等[1]在1987年提出,FPB被认为是一种高效的隔震装置. 此后,国内外专家从理论、试验以及应用等多方面对摩擦摆支座进行了研究[2-6],研究表明摩擦摆支座具有良好的隔震性能.由于FPB隔震性能好、造价较低、施工与维护简单等特点,欧美等发达国家已将其应用到许多重要结构中,如旧金山国际机场候机大厅、土耳其博卢高架桥、密西西比河I-40大桥等[7].
目前,通常应用弹簧阻尼单元代替FPB进行研究,弹簧阻尼单元的参数则通过FPB滞回性能获得[8-10],很难分析竖向和三维地震作用下应用摩擦摆支座结构的动力响应,为此,文献[11]将较精细化FPB有限元模型应用到K8型单层球面网壳结构中,分析了水平地震作用下应用FPB结构的地震响应规律;文献[12]将更精细化FPB有限元模型应用到K8单层球面网壳结构,分析了多维地震作用下FPB的隔震效果.
本文应用文献[12]中建立的精细化FPB有限元模型,对水平和竖向地震作用下网壳结构进行地震响应分析,探讨了FPB参数(摩擦系数和曲率半径)的影响规律.此外,在上述研究基础上,对单层球面网壳结构如何选择FPB进行了初步探讨.
1 FPB减震机理
滑槽、滑块与盖板构成整个摩擦摆支座,见图1,R为球形滑面的曲率半径.根据文献[12]可知,FPB通过隔震和耗能两种方式进行减震,因此,可以从两方面对FPB减震机理进行分析,一方面是通过滑块与滑面之间相互滑动隔离地震,另一方面是滑块与滑面之间相互摩擦耗能减震.
首先,从隔震方面进行分析,图2给出滑块在滑面上的受力,G、N和T分别为上部结构的重力、支反力和滑动摩擦力,根据力平衡条件水平剪力F可表达为[12]

应用FPB结构体系的运动方程可写为[12]

式中:M、C和K是上部结构质量、阻尼和刚度矩阵,Q为地震影响因子矩阵,Ü、ù和U分别是上部结构相对于基础的加速度、速度和位移,Üg和Üb分别是地面加速度和支座相当地面的加速度.

图2 滑块受力
其次,从摩擦耗能方面分析减震机理,传统结构能量方程可写为[13]

式中:E为外界传递给结构体系的总能量,Ee、Ek、Ec和Eh分别为结构体系弹性应变能、动能、粘滞阻尼耗能以及体系的滞回耗能.安装FPB结构能量方程为
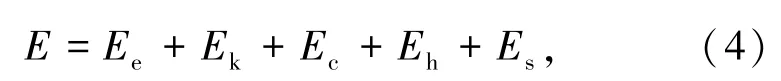
其中Es为FPB装置耗能.
2 有限元模型建立
2.1 FPB模型建立
FPB采用文献[12]所建立的精细化有限元模型,图1中标明支座具体尺寸,D1、D2和d的值分别取35、30和20 cm,经验证尺寸满足要求(滑槽为刚性面,分析摩擦摆支座滑块,静力时最大应力在140 MPa左右,动力时(PGA为400 gal)最大应力在190 Mpa左右),盖板、滑块和滑面单元尺寸越小,计算结果越精确,但计算时间越长,当盖板和滑块单元尺寸小于5 cm,滑面单元最大尺寸小于8 cm时,单元大小的变化对结构响应影响较小,因此取上述尺寸进行网格划分;盖板与滑块以及滑块与刚性面之间通过接触连接(在LS-DYNA软件中采用自动的点面接触,除摩擦系数外,其余参数采用默认值),上部结构与盖板顶面多个节点耦合连接(防止盖板转动).
2.2 网壳结构有限元模型
选用K8型单层球面网壳作为研究对象,网壳结构斜杆、环杆和肋杆截面尺寸分别为φ159×6、φ180×8和φ180×8,为加强结构整体刚度,最外环杆件截面尺寸选用φ299×10的杆件[12],网壳结构的屋面荷载1 kN/m2,荷载转化为质量单元作用在网壳节点上;有限元建模时,杆件用BEAM161单元建立,质量单元选用 MASS166建立,结构阻尼比为0.02,材料的弹性模量为2.06×105MPa,泊松比为0.3.对结构采用完全弹性假设,节点刚接,支座选用固定铰支座和FPB,均安装在最外环节点的下部,网壳平面图和支座布置见图3,图中ο表示铰支座和FPB的安装位置.

图3 摩擦摆支座布置位置
3 FPB隔震影响规律
为研究FPB参数(摩擦系数和曲率半径)对网壳结构地震响应规律的影响,FPB参数和加载方案见表1,方案1是研究支座摩擦系数的影响,方案2是研究支座曲率半径的影响.

表1 FPB参数及加载方案
3.1 对比指标
以曲率半径1 m,摩擦系数0.1的FPB为例,对两种支座形式(铰支座和FPB)的网壳结构分别施加水平和竖向Taft波,地震动强度均为400 cm/s2,K8型单层球面网壳结构部分地震响应的最大值见表2.
分析表2可知:除最外环杆件外,应用FPB结构各种地震响应均相应减小,如结构顶点峰值加速度在水平和竖向地震作用下分别减小79.21%和89.85%;当FPB代替铰支座应用到网壳结构中时,结构的水平支承明显减弱,网壳结构的最外环杆件则起到约束结构水平变形的作用,这使得杆件内力急剧增加,因此,加强最外环杆件是合理的.
以水平地震动作用为例,结构顶点加速度、位移以及能量时程曲线见图4,FPB网壳结构顶点加速度明显减小;两种支座形式下,结构顶点位移时程曲线的整体形式是相似的,这是因为网壳结构的自振周期和FPB周期相近,分别为1.89和1.98 s,但应用FPB后,曲线的波动明显减弱.为分析FPB对结构整体地震响应的影响,从结构能量、节点及杆件动力响应几个方面分别进行了分析.首先,由图4(c)可知,FPB网壳结构动能被明显减弱;其次,图5给出了结构节点加速度、相对位移(结构中节点相对最外环节点的平均位移)和杆件动应力最大值,由图5可得,应用FPB后,动应力、加速度和相对位移最大值都明显被减小;此外,应用FPB后,由于结构水平约束的减弱,在地震作用下,结构最外环节点之间存在较小相对位移.分析图5还可得出,与铰支座结构相比,FPB网壳结构的不同杆件动应力、节点加速度和水平相对位移的最大值相差较大,如,以杆件动应力为例,铰支座结构杆件动应力的变化区间为(0,200)MPa,而FPB结构则为(0,35)MPa.
由于网壳结构的杆件和节点数目较多,不可能对结构的所有杆件和节点进行逐一对比,为了研究结构的地震响应规律,本文采用文献[14]给出的3种评价指标进行研究,3种指标分别为动应力减震系数、相对位移减震系数以及加速度减震系数.

图4 结构顶点及能量动力响应时程曲线

图5 网壳结构节点及杆件最大动应响应
3.2 摩擦系数的影响
3.2.1 水平地震作用
选取表1中方案1研究FPB摩擦系数的影响,得到减震系数变化曲线见图6.减震系数都小于1,说明水平地震作用下,FPB能够有效减小网壳结构的动力响应;不同地震波作用下,减震系数的变化趋势相似,以El-Centro波为例分析摩擦系数对FPB隔震性能的影响规律,动应力和加速度减震系数(图6(a)和(b))的变化趋势是先减小后增加,而且随着地震动强度增加,这种变化趋势越明显,所有曲线的最小值多数在区间(0.05,0.15)上;分析图6(c)、(f)可得,随着摩擦系数增加,节点相对位移增加,这是因为随着摩擦系数增加,部分FPB进入粘滞状体(由于不同支座的竖向力不同,所以进入粘滞状体的时刻也不同),使得结构的变形增加,但当摩擦系数大于0.15时,随着摩擦系数增加,节点相对位移缓慢增加,这是因为摩擦系数大于0.15时,所有支座都进入粘滞状态,而且随着摩擦系数增加逐渐接近铰支座.

图6 水平地震作用下FPB摩擦系数的影响
3.2.2 竖向地震作用
选取表1中方案1研究竖向地震作用下FPB摩擦系数的影响,得到减震系数变化曲线见图7.分析结构动应力和加速度减震系数的变化(图7(a)、(b)、(d)、(e))可得:随着摩擦系数的增加,减震系数先减小后增加,这说明随着摩擦系数的增加,结构杆件的动应力和节点加速度都是先减小后增加,各曲线的最小值都在区间(0.075,0.20)上,而且随着地震动强度的增加,摩擦系数的最优区间也增加(最小值所对应的最小区间),以Taft波为例(图7(d)和(e)),70、140、220和400 cm/s2所对应的最小值区间分别为(0.075,0.125)、(0.075,0.125)、(0.1,0.15)和(0.15,0.20);分析结构节点Z向相对位移(图7(c)和(f)),随着FPB摩擦系数的增加,减震系数的值逐渐减小,说明结构整体变形减小,这是因为随着摩擦系数增加,结构所受水平支承能力增强(结构竖向刚度增加),从而使结构竖向变形减小,此外,减震系数小于1所对应的最小摩擦系数随着地震动强度的增加而增大,见图7(f),70、140、220和400 cm/s2所对应的摩擦系数分别为0.075、 0.10、0.125和0.175,因此,在上述摩擦系数最优区间上能保证结构的整体变形减小.

图7 竖向地震作用下FPB摩擦系数的影响
3.3 曲率半径的影响
3.3.1 水平地震作用
选取表1中方案2研究水平地震作用下曲率半径的影响,得到减震系数变化曲线见图8.减震系数的值都小于1,并且随着曲率半径的增加,减震系数的整体变化趋势逐渐减小,说明FPB具有显著隔震效果,并且随着曲率半径的增加,隔震效果增强;当摩擦摆支座曲率半径小于1m时,支座隔震较差,这与文献[10]所得结论相似;当支座的曲率半径在1~1.5 m时,结构的自振周期与FPB的周期(1.98~2.43 s)相近,由于共振,结构的地震响应增大,因此,图8在区间(1,1.5)的点规律性较差;曲率半径大于2m时,各曲线接近水平,这说明曲率半径大于2 m的FPB隔震效果相近.

图8 水平地震作用下FPB曲率半径的影响
3.3.2 竖向地震作用
选取表1中方案2研究竖向地震作用下曲率半径对网壳结构地震响应的影响,得到减震系数变化曲线见图9.减震系数的变化曲线都接近水平,这说明竖向地震作用下,曲率半径的变化对网壳结构地震响应的影响较小.分析结构杆件动应力和节点加速度减震系数(图9(a)、(b)、(d)、(e))可得,减震系数明显都小于1,这说明不同曲率半径的FPB都能有效地减小结构杆件的动应力和节点的加速度;分析结构节点竖向相对位移(图9(c)和(f))的变化趋势,随着地震动强度增加,减震系数值增大,并逐渐大于1,这说明网壳结构的整体变形逐渐增加.
3.4 摩擦摆支座选取原则
根据前面分析可得,应用摩擦摆支座的K8型单层球面网壳结构能够有效地抵抗地震作用,并且单层球面网壳结构选用不同参数(摩擦系数和曲率半径)摩擦摆支座时,结构的地震响应也不同,当选用合适的摩擦摆支座时,能够更有效地减弱单层球面网壳结构的地震响应,因此,单层球面网壳结构选择摩擦摆支座应该遵循一定的原则.由于不同地震波之间差异较大(如,频率、能量等),当峰值加速度(PGA)相同时,不同地震波引起结构的动力响应也不尽相同,因此,网壳结构在El-Centro和Taft地震波作用下的响应规律存在差异,见图6、7,但结构响应规律的变化趋势相似,因此,可以根据此种相似性给出单向地震作用下单层球面网壳结构选择摩擦摆支座的基本原则.

图9 竖向地震作用下FPB曲率半径的影响
首先,FPB摩擦系数的选取.两种地震动作用下(水平和竖向),分析图6(a)、(b)、(d)、(e)以及图7(a)、(b)、(d)、(e)可看出,随着地震动强度的增加,减震系数最小值逐渐右移,即对应的摩擦系数逐渐增加,这说明FPB摩擦系数的最优区间逐渐增加,而且所有减震系数的最小值都在区间(0.05,0.20);分析图6(c)和(f)以及7(c)和(f)可得,水平和竖向地震作用下,网壳结构的变形规律相反,在水平地震作用下,减震系数的值都小于1,即结构的水平变形减小,而竖向地震作用下,随着摩擦系数的增加,结构竖向变形也减小.由以上分析可给出单向地震作用下网壳结构选择FPB摩擦系数的基本原则:摩擦系数尽量在区间(0.05,0.20)上取值,而且网壳结构的抗震级别越高,选择摩擦系数应该越大.
其次,FPB曲率半径的选取.分析图9可得,竖向地震作用下,曲率半径的变化对网壳结构地震响应的影响较小,因此,可根据结构在水平地震作用下的动力响应给出曲率半径的选取原则.分析图8可得,随着曲率半径的增加,网壳结构地震响应减弱,当曲率半径大于2m时,各曲线接近水平,这说明网壳结构地震响应保持不变.再分析图2可得,当FPB滑块与滑槽的相对位移一定时,曲率半径越大,由式(1)所得水平剪力就越小,结构的恢复性能就越差.因此,由以上分析可给出网壳结构选择FPB曲率半径的基本原则:在能提供较强恢复力的前提下,曲率半径越大越好.
4 结 论
1)地震作用下,应用摩擦摆支座K8型单层球面网壳结构的动能明显减弱,结构杆件的动应力、节点加速度和相对位移的最大值都明显减小.
2)摩擦系数的影响:随着摩擦系数的增加,结构杆件动应力和节点加速度先减小后增加;在水平和竖向地震作用下,结构变形的变化趋势正好相反,随着摩擦系数的增加,在水平地震作用下,结构的整体变形逐渐变大,而在竖向地震作用下,结构的整体变形逐渐减小.
3)曲率半径的影响:水平地震作用下,随着支座曲率半径的增加,网壳结构的地震响应减弱;竖向地震作用下,支座曲率半径的变化对网壳结构地震响应的影响较小.
4)网壳结构选择FPB的策略:应遵循网壳结构抗震级别越高摩擦摆支座摩擦系数越大的原则,并且尽量在某一区间上取值,如,矢跨比为1/5单层球面网壳结构,当FPB曲率半径为1 m时,摩擦摆支座的最优区间是(0.05,0.20);在确保FPB具有良好恢复性能的前提下,曲率半径的取值越大越好.
[1]ZAYASV,LOW S,MAHIN S.The FPS earthquake resisting system[R].Technical Report UCB/EERC-87/01,Berkeley:University of California at Berkeley,1987.
[2]PRANESH M,SINHA R.Earthquake resistant design of structures using VFPI [J].Journal of Structural Engineering,2002,128(7):870-880.
[3]WONGPRASERT N,SYMANSM D.Numerical evaluation of adaptive base-isolated structures subjected to earthquake ground motions[J].Journal of Engineering Mechanics,2005,131(2):109-119.
[4]JANGID R S.Optimum friction pendulum system for nearfaultmotions[J].Engineering Structures,2005,27:349-359.
[5]TSAICS,LU PC,CHENW S.Applications of trench and trajectory friction pendulum systems to seismicmitigation of structures[C]//Proc.14th WCEE.Beijing:[s.n.],2008.
[6]TSAIC S,LU P C,CHEN W S.Shaking table tests of a building isolated with a trench friction pendulum system[C]//Proc.of PVP2006-ICPVT11-93253,2006 ASME Pressure Vessels and Piping Conference, Seismic Engineering.Vancouver,BC:[s.n.],2006:1-5.
[7]Earthquake Protection Systems (EPS), Technical characteristics of friction pendulum bearings[EB/OL].(2002-04-15)[2014-08-16]http://www.Earthquake protection.com/TechnicalCharacteristicsofFPBearngs.pdf.
[8]王建强,丁永刚,李大望.摩擦摆支座恢复力模型研究[J].四川建筑科学研究,2007,33(3):25-27.
[9]HUW Y.Analysis effectiveness of bridges with partial isolation[D].Utah:Utah State University Logan,2008
[10]薛素铎,赵伟,李雄彦,等.摩擦摆支座在单层球面网壳结构隔震控制中的参数分析[J].北京工业大学学报,2009,35(7):933-938.
[11]孔德文,孙梦涵,支旭东,等.应用摩擦摆支座的单层球面网壳地震相应分析[J].土木工程学报,2012,45(增刊1):158-162.
[12]孔德文,范峰,支旭东,等.多维地震动作用下应用摩擦摆支座K8型单层球面网壳结构抗震性能研究[J].地震工程与工程振动,2014,34(4):195-200.
[13]周云.摩擦耗能减震结构设计[M].武汉:武汉理工大学出版社,2006.
[14]孙梦涵,范峰,支旭东,等.应用摩擦摆支座平板网架的抗震性能初步研究[C]//第十四届空间结构学术会议论文集.福州:中国建筑科学研究院,2012:266-277.
(编辑赵丽莹)
Isolation research of friction pendulum bearings in K8 single-layer reticulated domes
KONG Dewen1,2,FAN Feng1,2,ZHIXudong1,2
(1.Key Lab of Structures Dynamic Behavior and Control(Harbin Institute of Technology),Ministry of Education,150090 Harbin,China;2.School of Civil Engineering,Harbin Institute of Technology,150090 Harbin,China)
To obtain the seismic performance of single-layer reticulated domes with friction pendulum bearings(FPB),finite element refined models of FPB were applied to 80 m K8 single-layer reticulated domes FE Model.The same earthquake waves were exerted to single-layer reticulated shells with hinge support or FPB.The isolation effect of FPBswas analyzed in twomain aspects including the dynamic responses of bars and nodes of reticulated domes,and the impact of FPB parameters on the seismic response of single layer latticed shellwere discussed.The results indicate that the optimal friction coefficientof FPB increaseswith the increase of the groundmotion intensity.The bigger curvature radius of FPB,the smaller seismic responses of reticulated shell structurewill be.On the basis of the above research,this paper gave some discussion how friction pendulum bearingswere selected for single-layer reticulated domes.
single-layer reticulated dome;friction pendulum bearing(FPB);isolation;optimal friction coefficient;curvature radius
TU311.3
A
0367-6234(2015)12-0009-07
10.11918/j.issn.0367-6234.2015.12.002
2014-08-16.
国家自然科学基金重大计划集成项目(91315301);国家自然科学基金面上项目(51278152);黑龙江省杰出青年科学基金(JQ2010-10).
孔德文(1984—),男,博士研究生;范 峰(1971—),男,教授,博士生导师;支旭东(1977—),男,教授,博士生导师.
孔德文,kongdewen0608@126.com.

