高强热轧钢筋混凝土连续梁弯矩调幅计算方法
李 玲,王 英,郑文忠
(结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),150090哈尔滨)
高强热轧钢筋混凝土连续梁弯矩调幅计算方法
李 玲,王 英,郑文忠
(结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),150090哈尔滨)
为研究高强热轧钢筋混凝土连续梁弯矩调幅规律,对配置HRB335、HRB400、HRB500、HRB600热轧钢筋的392根混凝土连续梁进行非线性分析,分两阶段对弯矩调幅进行考察:一是从加载到支座控制截面纵筋受拉屈服引起的弯矩调幅βb;二是从支座控制截面形成塑性铰至受压区边缘混凝土被压碎引起的弯矩调幅βa.结果表明:高强热轧钢筋混凝土连续梁塑性铰出现推迟,塑性转动能力减小;同时从梁受拉边缘混凝土进入塑性至受拉钢筋屈服区间变长.获得了以支座控制截面相对塑性转角θp/h0为关键参数的具有一定截距βb的弯矩调幅系数曲线方程.为便于工程应用,建立以相对受压区高度ξ为自变量的实用化公式.
高强热轧钢筋;混凝土连续梁;非线性分析;弯矩调幅系数
连续梁弯矩调幅设计方法在工程设计中广泛应用,国内外学者对其进行了大量试验研究,其中多以考察塑性铰形成后结构的内力重分布来建立弯矩调幅系数计算方法.近年来,HRB400、HRB500和HRB600级钢筋相继引入相关标准[1],而CECS51—93《钢筋混凝土连续梁和框架考虑内力重分布设计规程》中弯矩调幅系数的取值是基于配置HPB235和HRB335的连续梁及框架试验结果和工程实践编制的.由于纵筋屈服强度提高,一是会存在较长的从受拉区混凝土进入受拉塑性—截面开裂—裂缝发展—纵筋受拉屈服的过程,这一过程中弯矩调幅幅度相对增大;二是塑性铰出现推迟,塑性铰转动能力减小,这点对弯矩调幅不利.因此,本文对钢筋混凝土两跨连续梁弯矩调幅分为两阶段考察:其一为从加载到支座控制截面纵筋受拉屈服引起的弯矩调幅幅度βb;其二为支座控制截面形成塑性铰至受压区边缘混凝土被压碎引起的弯矩调幅幅度βa.以弯矩调幅系数为纵坐标、支座控制截面相对塑性转角θp/h0为横坐标建立坐标系,将利用非线性分析程序计算所得数据点置于该坐标系中,拟合得到具有一定截距的曲线.该曲线对应纵轴截距即为第一阶段调幅幅度βb,高于βb以上部分即为第二阶段调幅幅度βa=β-βb.基于以上思路,对配置不同强度等级热轧钢筋的混凝土连续梁,建立与钢筋屈服强度相关的βb表达式以及以相对塑性转角θp/h0为自变量的βa表达式,并对其进行实用化处理以便于工程应用.
1 塑性铰的塑性转角计算
钢筋混凝土梁塑性铰的发生并不是集中于一点,而是在一个区域内,以受拉钢筋开始屈服为塑性铰出现的标志,以受压边缘混凝土被压碎(达到极限压应变)为塑性铰结束使命的标志.塑性铰实际长度为受拉钢筋应变不小于屈服应变的区段长度.两跨混凝土连续梁塑性内力重分布程度与中支座控制截面塑性铰的转动能力密切相关,计算塑性铰转角的基本参数包括:截面的极限曲率φu、截面的屈服曲率φy、等效塑性铰区长度Lp[2].其中屈服曲率是指控制截面受拉纵筋屈服时对应的曲率,通常用φy表示;极限曲率是指控制截面受压边缘混凝土达到极限压应变时对应的曲率,通常用φu表示;等效塑性铰长度是指按与实际塑性铰区长度内曲率分布曲线所围面积相等(保证塑性转角相等)的原则,将实际曲率分布等效为矩形分布后等效区域的长度,通常用Lp表示.采用条带积分法编制非线性分析程序,计算连续梁中支座控制截面的极限曲率φu和屈服曲率φy.由于受弯构件等效塑性铰长度Lp影响因素比较复杂,本文以计算简便为原则,基于国内外学者提出的等效塑性铰长度经验公式[3-7],通过程序模拟计算将等效塑性铰长度Lp表示为截面有效高度h0倍数的形式作为本文计算依据,如式(1)所示,具有一定精度.

确定3个基本参数后即可由式(2)计算塑性铰的塑性转角.:

2 弯矩调幅系数β计算公式
2.1 试件设计
设计392根两跨钢筋混凝土连续梁进行非线性计算分析,采用两种荷载形式分别为跨中单点加载和均布加载.模拟梁试件尺寸为:h=400 mm,b=200 mm,单跨计算跨度为6 000 mm.GB50010—2010《钢筋混凝土结构设计规范》中已纳入较高强度等级混凝土,本文选用混凝土强度等级为C20~C80,受拉钢筋强度等级为HRB335、HRB400、HRB500、HRB600.通过统计材性试验结果,得到各强度等级混凝土及钢筋力学性能指标见表1、2.钢筋配置采用控制变量与程序试算相结合方式:中支座截面钢筋的配置以截面相对受压区高度为控制参数,分别取为ξ=0.1~0.4,其中当混凝土强度等级较高时,截面界限相对受压区高度小于0.4,则取界限受压区高度为最大值;梁跨中截面配筋根据中支座截面配筋采用程序进行试算,使最终破坏状态为跨中截面受拉钢筋屈服或接近屈服同时中支座混凝土受压边缘达到极限压应变.

表1 模拟梁混凝土物理力学指标

表2 模拟梁钢筋物理力学指标
2.2 弯矩调幅系数计算及分析
采用共轭梁法[7]计算两跨混凝土连续梁内力,进而得到弯矩调幅系数β为

将利用非线性程序计算所得数据点置于以相对塑性转角θp/h0为横坐标、β为纵坐标的坐标系中,得到在跨中集中荷载和均布荷载作用下配置不同强度等级钢筋的两跨混凝土连续梁弯矩调幅系数β的拟合曲线见图1、2.
由拟合曲线可看出,两跨混凝土连续梁的弯矩调幅过程可分为两个阶段:第一个阶段是从开始加载到中支座控制截面受拉钢筋屈服,这一过程中的调幅幅度是由受拉区混凝土的塑性变形及裂缝引起刚度变化而引起的,用βb表示;第二阶段是中支座控制截面开始形成塑性铰至截面受压边缘混凝土达到极限压应变,这一过程中的调幅幅度是由于塑性铰转动引起的,用βa表示.因此,β可表示为


图1 集中荷载作用下模拟计算点分布及拟合曲线
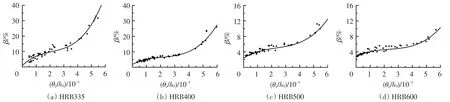
图2 均布荷载作用下模拟计算点分布及拟合曲线
βb对应所拟合曲线中的截距值,不同荷载作用下βb见式(5).在两种荷载形式作用下βb值均随钢筋屈服强度的提高而增大,这是由于钢筋屈服强度增大,连续梁从截面受拉区混凝土进入受拉塑性—截面开裂—裂缝发展—纵筋受拉屈服这一过程变长,而混凝土强度等级变化影响很小,故公式中不予考虑.由于实际工程中构件往往并不只承受单一的荷载形式且不同荷载作用下调幅系数拟合曲线形式相似,因此可建立不同荷载作用下钢筋屈服强度fy与βb的统一关系式(6),见图3.
集中荷载作用下:
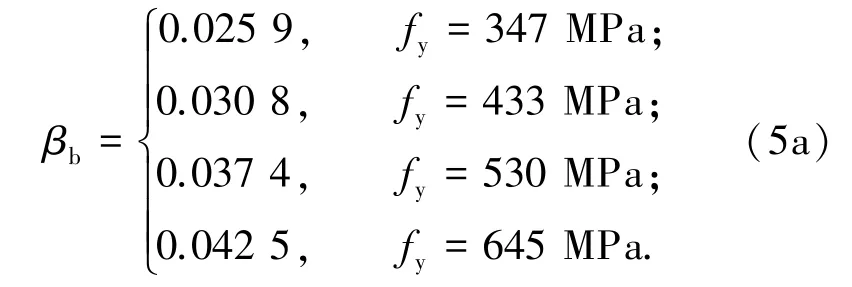
均布荷载作用下:
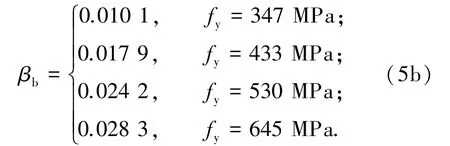

βa对应高于截距以上的弯矩调幅幅度即βa=β-βb,随着相对塑性转角θp/h0增加而增大.以βa为纵坐标、θp/h0为横坐标重新建立坐标系,对各模拟数据点拟合具有95%保证率的下包线,见图4,得到以θp/h0为自变量的βa的统一表达式(7).之所以采用拟合下包线的方式,是由于在实际工程应用中利用下包线的计算结果偏安全.
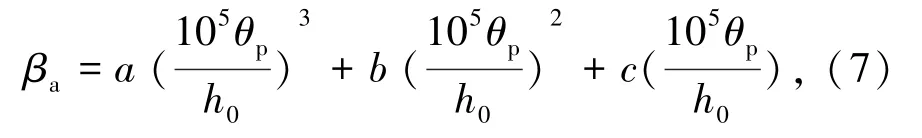
其中:HRB335级钢筋a=0.427,b=-2.056,c=4.653;
HRB400级钢筋a=0.213,b=-1.200,c=3.419;
HRB500级钢筋a=0.087,b=-0.545,c=1.756;
HRB600级钢筋a=0.035,b=-0.180,c=0.850.
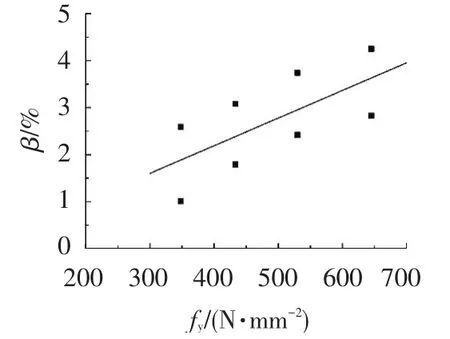
图3 βb与fy关系

图4 不同荷载作用下θp/h0与βa的统一
3 计算公式实用化处理
βa的计算式(7)以θp/h0为自变量,计算相对繁琐,对βa计算式进行实用化处理,建立考虑多种影响因素的以截面相对受压区高度ξ和钢筋级别为自变量的βa函数表达式.
3.1 参数分析
采用控制变量法分析跨高比、荷载形式、混凝土强度等级、钢筋屈服强度以及相对受压区高度等因素对弯矩调幅系数影响,利用非线性计算程序得到各参数影响规律见图5~9,在其它参数不变情况下,β随着跨高比l/h、混凝土强度等级、钢筋强度等级和ξ的增加而减小.
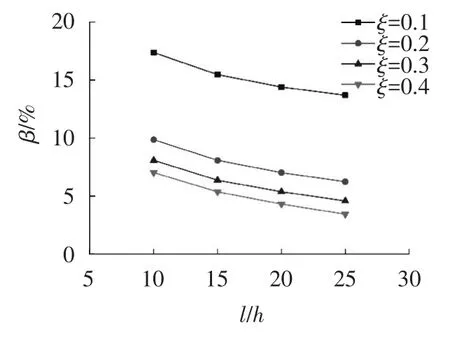
图5 跨中集中荷载作用下β随l/h的变化

图6 均布荷载作用下β随l/h的变化

图7 不同荷载形式下β的变化
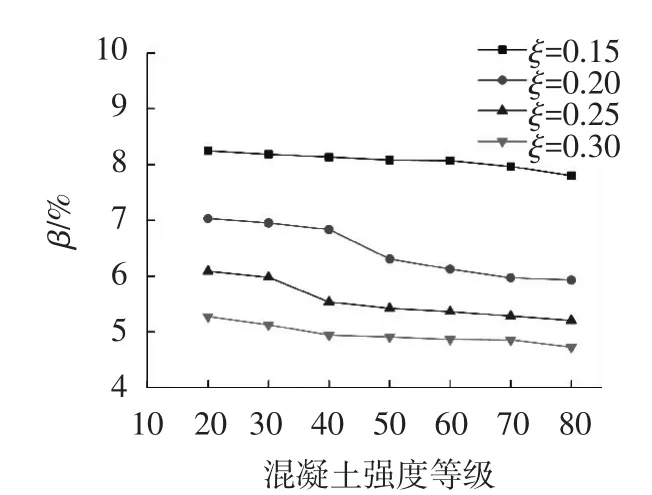
图8 β随混凝土强度等级的变化

图9 β随钢筋屈服强度fy的变化
3.2 弯矩调幅系数实用化公式
为考虑l/h对弯矩调幅系数的影响,引入系数μ表示在中支座相对受压区高度ξ、配置钢筋强度等级以及作用荷载形式等基本参数均相同的情况下,l/h=10、15、20、25的两跨混凝土连续梁与l/h=15的两跨混凝土连续梁弯矩调幅系数的比值,见图10.根据有限元模拟计算结果,得到l/h与μ的关系式(8).

其中:HRB335级钢筋,λ=-0.020,k=1.23;HRB400级钢筋,λ=-0.025,k=1.34;HRB500级钢筋,λ=-0.032,k=1.44;HRB600级钢筋,λ=-0.037,k=1.58.
以l/h=15的两跨钢筋混凝土连续梁为基础,建立βa计算公式.以中支座截面相对受压区高度ξ为横坐标,第二阶段βa为纵坐标建立坐标系,配置不同强度等级钢筋模拟梁的计算结果分布图及拟合曲线见图11,公式为

其中:HRB335级钢筋,η=0.35,ν=-1.91;HRB400级钢筋,η=0.33,ν=-1.71;HRB500级钢筋,η=0.17,ν=-1.66;HRB600级钢筋,η=0.04,ν=-2.25.
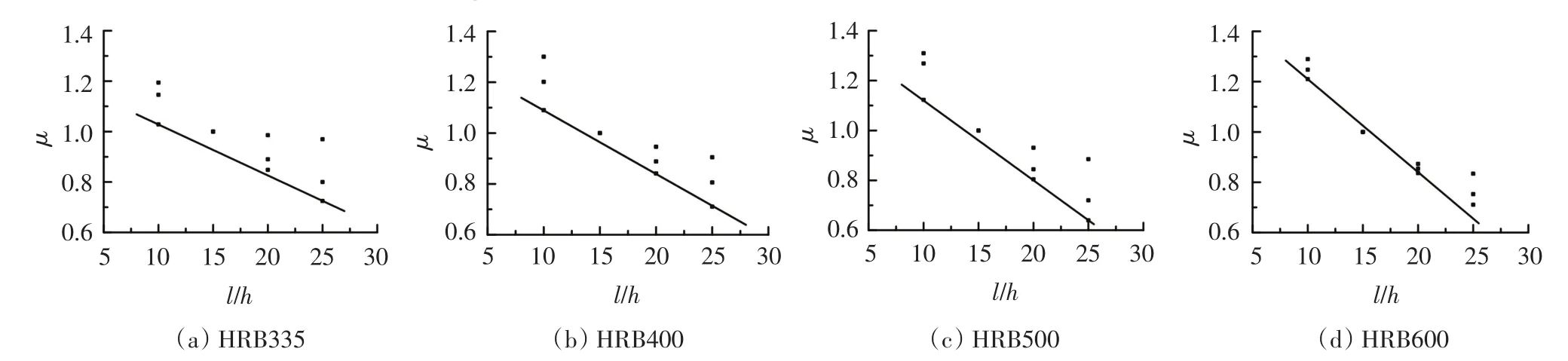
图10 影响系数μ与跨高比l/h关系

图11 ξ与βa关系
将βa计算式(9)和βb计算式(6)代入式(10),即可求得两跨混凝土连续梁弯矩调幅系数为

本公式适用于混凝土强度等级为C20~C80的常规钢筋混凝土连续梁,为保证结构裂缝及变形满足正常使用极限状态要求,公式中β≤30%.至此,本文建立了考虑钢筋屈服强度、相对受压区高度、跨高比、荷载形式等因素的弯矩调幅系数计算公式,实现了配置高强钢筋与普通钢筋的统一计算方法.
3.3 结果验证
为了验证拟合公式的适用性与精确性,分别选取文献[8-10]中配置不同钢种的两跨钢筋混凝土连续梁,利用本文公式及各国规范规定计算试验梁弯矩调幅系数,见表3.本文提出弯矩调幅公式计算值与试验实测值吻合程度较好,说明该公式具有一定精度.其中,中国规范规定钢筋混凝土连续梁支座负弯矩调幅幅度不宜大于25%;弯矩调整后梁端截面相对受压区高度不应超过0.35且不宜小于0.10[1].从表3对比可看出,中国规范以限值的形式规定弯矩调幅系数大小,并没有考虑钢筋强度等级、相对受压区高度及应变渗透的影响,应进一步科学化.

表3 调幅系数计算结果
4 结 论
1)将热轧钢筋作纵筋的混凝土连续梁弯矩调幅分两阶段进行考察:一为从加载至支座控制截面受拉钢筋屈服过程中塑性发展所引起的弯矩调幅βb;二为从支座控制截面形成塑性铰到截面受压边缘混凝土达到极限压应变过程中所引起的弯矩调幅βa.随着塑性转角的增大弯矩调幅βa增大;当相对受压区高度ξ相同时,随着钢筋屈服强度的增高第一阶段调幅βb增大、第二阶段调幅βa减小,总弯矩调幅减小.
2)通过参数化分析发现弯矩调幅系数随着跨高比l/h、混凝土强度等级、钢筋强度等级和相对受压区高度ξ的增大而减小.建立了考虑各影响因素的实用化计算公式(10)以便于实际应用.
本文分析没有考虑钢筋在支座宽度范围内应力渗透对弯矩调幅的有利影响,在后续工作中应进行完善.
[1]GB50010—2010混凝土结构设计规范[S].北京:中国建筑工业出版社,2011.
[2]郑文忠,李和平,王英.超静定预应力混凝土结构塑性设计[M].哈尔滨:哈尔滨工业大学出版社,2002.
[3]PARK R,PAULAY T.Reinforced concrete structures[M].New York:John Wiley&Sons,1975.
[4]杨春峰,朱浮声,郑文忠.无粘结预应力混凝土梁塑性铰的研究[J].低温建筑技术,2005(5):53-54.
[5]段炼,王文长,郭苏凯.钢筋混凝土结构塑性铰的研究[J].四川建筑科学研究,1983(3):16-22.
[6]沈聚敏,翁义军.钢筋混凝土构件的变形和延性[J].建筑结构学报,1980,1(2):47-58.
[7]朱伯龙,董振祥.钢筋混凝土非线性分析[M].上海:同济大学出版社,1985:42-49.
[8]邓宗才.钢筋混凝土连续梁弯矩调幅法的研究[J].建筑结构,1997(8):30-32.
[9]李美云.HRB400级钢筋混凝土构件受力性能的试验研究[D].郑州:郑州大学,2003.
[10]王全凤,刘凤谊,杨勇新.HRB500级钢筋混凝土连续梁抗弯试验研究[J].四川建筑科学研究,2008,34(4):14-17.
[11]Building Code Requirements for Structural Concrete(ACI318-08)and Commentary[S].ACICommittee,American Concrete Institute,International Organization for Standardization,2008.
[12]BS 8110-1:1997,Structural use of concrete:Part1.Code of practice for design and construction[S].British Standards Institution,1997.
(编辑赵丽莹)
M omentmodulation design method of reinforced concrete continuous beam w ith high-strength hot-rolled bar
LILing,WANG Ying,ZHENGWenzhong
(Key Lab of Structures Dynamic Behavior and Control(Harbin Institute of Technology),Ministry of Education,150090 Harbin,China)
392 two-span continuous beams which are used HRB335,HRB400,HRB500 and HRB600 reinforcements are analyzed to investigate the bending moment amplitude modulation rule of concrete continuous beam with high-strength hot-rolled bar.The moment redistribution is investigated in two phases:One is the modulation amplitudeβbcaused from loading to steel yielding in control section of support.The other isβacaused from formation of a plastic hinge to the crushing of compressive extreme concrete fiber in control section of support.The results indicate that the plastic hinge appears delay and the rotation capacity of plastic hinge decreases,at the same time,the interval from the tensile extreme concrete fiber into the plastic to longitudinal reinforcement yielding ranges longer.The moment amplitude modulation coefficient equation usingθp/h0as the key parameters with a certain interceptβbhas been obtained.Practical expression withξas independent variable has been proposed to facilitate the engineering applications.
high-strength hot-rolled bar;continuous beam;non-linear analysis;momentmodulation
TU375
A
0367-6234(2015)12-0016-05
10.11918/j.issn.0367-6234.2015.12.003
2014-08-16.
国家自然科学基金(51378146);国家教育部长江学者奖励计划资助项目(2009-37);教育部博士点基金资助项目(20132302110064).
李 玲(1990—),女,博士研究生;郑文忠(1965—),男,博士生导师,长江学者特聘教授.
王 英,wangying888@hit.edu.cn.

