基于自适应遗传算法的电网参数检测的研究

余胜男，许晓彦

（上海海事大学物流工程学院，上海201306）

0 引 言

电力系统中，电压的振幅、频率和相位是三个非常重要的参数。对电压频率检测的研究由来已久，最原始的方法是过零检测法，发展到后来用的最多最为经典的是傅里叶算法，傅里叶变换［1，2］建立以时间为自变量的信号和以频率为自变量的频谱函数之间的转换关系，速度快、精度高，算法简单，但是不可避免地出现频谱泄露和栅栏效应，针对这种缺陷也出现了诸多改进算法［3，4］。随着计算机技术的发展，智能优化算法的应用不再受计算速度的限制，如小波分析、人工神经网络等。同时参数化分析方法也大受亲睐，如最小二乘法、卡尔曼滤波［5］和自适应滤波算法［6］等。这些算法在虽然精度上取得了不错效果，但是算法非常复杂，降低了测量速度。遗传算法［7］作为一种智能算法用于电网参数检测，是一个全新的领域。遗传算法结合参数化估计的自适应算法形成了自适应遗传算法［8］，通过动态的改变交叉和变异概率，弥补了传统遗传算法的早熟，搜索速度慢等缺陷，同时保留了搜索的全面型和精确性。与传统的遗传算法相比，其收敛速度和精度都有了较大的提高。

1 系统建模

为了应用自适应遗传算法，需要先将参数测量问题转化为求目标函数最优解问题。目标函数的生成过程介绍如下：

理想的电网电压可以表示为：

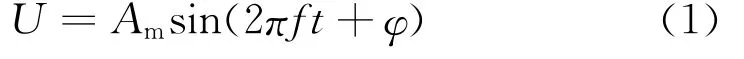
式中，Am为电网电压的幅值；f为频率；φ为相位。假设电网实际电压为u，以Δt为采样间隔，对其进行采样，每周期采样n次，tn时刻，实际电网电压采样值为un。设第n次采样对应的理想电压的样本表示为：

则第n次误差可表示为：

采样n次的总误差为

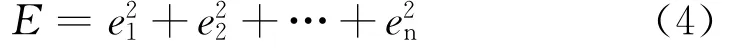
由于遗传算法求最大值更加方便、更为常用，所以将目标函数取为

式中，C为一较大常数，可以保证Obj为正数。可知，当电网电压的频率、振幅和相位越接近理想值时，E便越小，Obj则越大。如此一来，就将对电网电压的频率、振幅和相位的检测问题转化为了求Obj的最大值的问题。

2 自适应遗传算法

遗传算法是一种模拟自然界法则物竞天择，适者生存的生物进化的一种智能优化算法。自适应遗传算法（Adaptive Genetic Algorith m，AGA）是对基本遗传算法的一种改进，它通过对遗传参数的自适应调整，大大提高了遗传算法的收敛精度，加快了收敛速度。下面是自适应遗传算法测量电网电压振幅、频率和相位的具体步骤。

2.1 编码

在自适应遗传算法中，用一串二进制数来代表一个变量。如下：

本文中一条二进制编码由48位组成，前16位代表振幅，中间16位代表频率，后16位代表相位，其数值范围分别如表1所示。

表1 AGA编码位数和范围

2.2 挑选优良种群

本文采用轮盘赌的方式进行挑选操作，直接以目标函数值作为适应度，个体Ψ1，其适应度就为其代入目标函数所得的值Obj（Ψ1），如果挑选N个个体进入下一代，则Ψ1被挑中的概率为：

很明显，个体的目标函数值越大，其适应度就越高，被挑中存活的概率也就越大。

2.3 交叉

不同于标准遗传算法，自适应遗传算法的交叉概率是随着遗传过程，自适应变化的。在开始阶段，交叉概率要大一些，有利于保持种群的多样性；而在后期，交叉概率要小一些，以进行细致的搜索，防止破坏最优解。本文设置交叉概率随迭代次数线性变化，由最初的0.9减小到最终的0.3。

2.4 变异

遗传算法中，变异的概率过大，会破坏最优解，变异的概率过小，又会出现早熟现象。本文设置变异概率随迭代次数的增加由大变小，由最初的0.01减小到最终的0.001。

2.5 寻找最优解

每次迭代完，记录最优解并保留下来。剩余的群体再次经过选择复制，自适应交叉和变异，形成新一代种群。这样可以保证后一次的迭代一定会比前一次迭代的适应度更高。整个迭代过程完成之后所产生的最优解对应的个体就是适应度最高的个体。

2.6 遗传算法各参数设置及程序流程图

表2所示为本文所用的自适应遗传算法的各项参数，图1为算法的程序流程图。

表2 本文采用的AGA参数

图1 自适应遗传算法（AGA）程序流程图

3 仿 真

图2和图3分别是运用GA和运用AGA进行仿真的结果，对比两图，不难看出自适应遗传算法相对于遗传算法，稳定性更好，收敛速度更快，收敛精度也更高。迭代40次所用的时间大概在0.4 s，其实迭代10次足矣，时间能在0.1 s以内。

图4是两种算法平均适应度的对比，可以看出，遗传算法本身每次迭代的平均适应度波动非常大，不稳定，而加入了自适应调整之后，整个自适应遗传算法的稳定性都增加了。表3是误差对比，可以看出AGA整体误差更小。

图2 标准遗传算法（GA）仿真结果

图3 自适应遗传算法（AGA）仿真结果

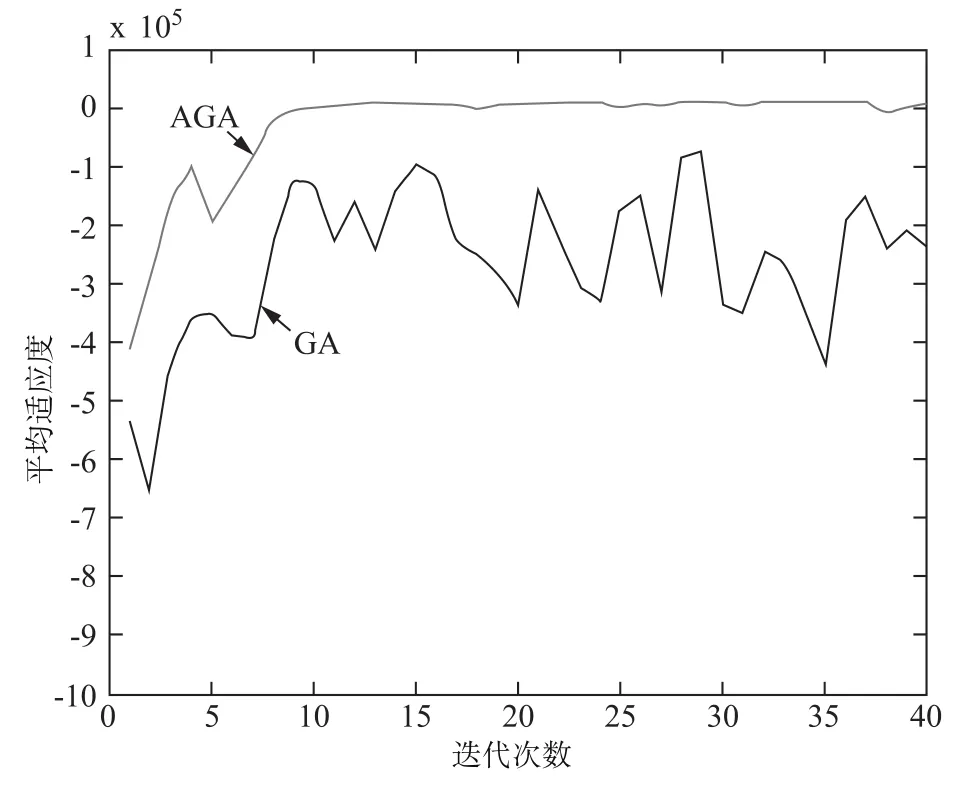
图4 GA与AGA的平均适应度对比

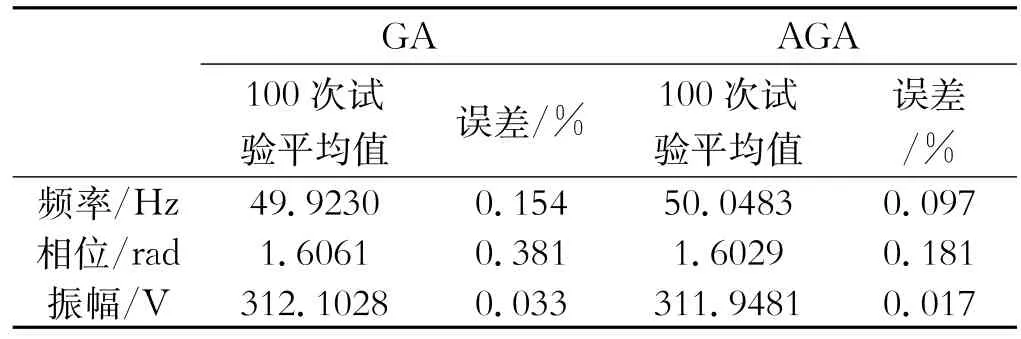
表3 GA与AGA误差对比

4 结 论

本文将遗传算法引入到电网参数的测量中，验证了其可行性，并且加入自适应算法，得到了比传统遗传算法更好的效果。自适应遗传算法不仅能同时测量振幅、频率和相位，而且测量结果精度高、速度快，完全能满足测量要求。

［1］ Borkowski J，Kania D，Mroczka J.Interpolated-DFTBased Fast and Accurate Frequency Estimation for the Control of Power［J］.IEEE Transactions on Industrial E-lectronics，2014：7026-7034.

［2］ 王天健，吴振升，王 晖，刘 栋.基于快速傅里叶变换的电力系统频率实时计算方法［J］.郑州大学学报（工学版），2011，32（3）：81-84.

［3］ 叶 芳，焦彦军.一种基于傅立叶算法的高精度测频方法［J］.电力系统保护与控制，2012，40（8）：44-48.

［4］ 蒋春芳，刘 敏.基于双插值FFT算法的间谐波分析［J］.电力系统保护与控制，2010，38（3）：11-14.

［5］ 罗谌持，张 明.基于Sigma点卡尔曼滤波器的电力频率跟踪新算法［J］.电力系统自动化，2008，32（13）：35-39.

［6］ 高 玮，何正友，基于时间尺度变换策略的幅频测量用自适应陷波器算法［J］，电网技术，2012，36（3）：127-133.

［7］ Denis V Coury.Frequency Estimation Using a Genetic Algorithm With Regularization Implemented in FPGAs［J］.IEEEtransaction on smart grid，2012，3（3）：1353-1361.

［8］ Fujun Wang，Junlan Li，Shiwei Liu，Xingyu Zhao，Dawei Zhang，Yangling Rian.An Improved Adaptive Genetic Algorithm for Image Segmentation and Vision A-lignment Used in Microelectronic Bonding［J］.IEEE／ASME Transactions on Mechatronics，2014，19（3）：916-923.