一维噪声子空间算法在DOA应用中局限性的研究*

刘建新

(中国空空导弹研究院 洛阳 471000)



一维噪声子空间算法在DOA应用中局限性的研究*

刘建新

(中国空空导弹研究院 洛阳 471000)

对一种应用于DOA中的“一维噪声子空间算法”进行了讨论,指出了现有关于该算法某些结论的失误,同时讨论了在不同入射角情况下时,该算法的应用局限性。计算表明,虽然一维噪声子空间算法存在理论和应用上的局限性,但在符合应用条件时仍计算出了较为满意的DOA的结果,同时大大降低了计算量,所以仍有其实用价值。

相控阵通信天线; 经典MUSIC算法; 一维噪声子空间算法

Class Number TN82

1 引言

在军用无线通信领域,由于相控阵天线具有传统天线难以比拟的优势,因而越来越被人们重视。相控阵通信天线很多能力的实现需要依靠对当前来波方向的自主估计,因此,来波方向估计(Direction of Arrival,DOA)的算法被研究者们所关注。

MUSIC算法是DOA估计中的经典算法之一。MUSIC算法在运算时采用循环迭代的形式,依次估计到达角矩阵的参数直至收敛。在这类循环迭代中,对于各种估计都需要通过多维搜索获得,这种运算的计算量本就很庞大,而且随着阵元数增加,计算量会呈指数增长。因而,对算法的简化是有意义的。

近年来,一种旨在简化经典MUSIC算法的“一维噪声子空间算法”被提出,但是现有的诸多文献在此方面的分析还不够准确,但这种思想可以为改进DOA算法提供一些启示和改进途径。

2 一维噪声子空间的算法推导

在众多的信号DOA估计算法中,基于接收信号相关矩阵特征分解的MUSIC算法,具有良好的DOA估计性能,其估计方差接近Cramer-Rao下界[6～7]。但是,在实际应用中,由于快采样拍数有限,其所接收到的含有噪声信号,总是与理想信号有一些差值,快拍数越少、信噪比越小,这种差值可能越显著。这样的结果就是,在实际运算中出现了被称作“特征值泄露”的问题。通过计算机仿真计算也可以看到,当信噪比较低和快拍数有限时,阵列相关矩阵的特征分解结果,并不像MUSIC算法理论上所期待的那样,噪声子空间中M-D个小特征值相等且等于噪声方差,而是变成了一系列大小不一的分布。这样,就很难根据小特征值的重数来确定噪声子空间的维数,也无法根据小特征值所对应的特征向量构造准确的噪声子空间,这使算法对到达角的估计性能严重下降。为了克服这个问题,一种经过修正MUSIC算法被提出。

在理想情况下,接收信号协方差矩阵的每个噪声特征向量都分别正交于阵列的每个信号向量和信号子空间,即当阵列流型a(θi)与任意一个噪声特征向量正交时,所对应的θi即为入射信号的来波方向估计值。也就是说,MUSIC算法是阵列流型a(θi)应与任意一个噪声特征向量相正交,即:

‖aH(θ)UN‖2=0

(1)

此时,接收信号矩阵的特征值可以排列为

λ1>λ2>…>λD=λD+1=…=λM=σ2

(2)

文献[5,8]中认为,在实际计算时,由于信噪比较低和快拍数有限、记录的接收信号不准确等原因,对相关矩阵的特征分解已不能理想地反映应有的正交情况,原有的噪声特征向量已不再最小、相等且等于噪声方差,而是变成:

λ1>λ2>…>λD>λD+1>…>λM=σ2

(3)

也就是发生了所谓“特征值泄露”现象。此时,显然已经没法根据小特征值的重数来判断入射信号个数,更无法利用原有的正交特性来估计到达角,进而,就没法据此估计来波方向了。文献[5]等认为,各个特征值中,只有最小的特征值及其特征向量,最接近真实值,那么可以假设,此时只有最小特征值是实际噪声特征值。在这种情形下,原有的由噪声特征值所对应的特征向量所张成的M-D维噪声子空间,就由最小特征值对应的特征向量构成的一维空间所代替了。那么,原有的正交关系,变成这样了这样:

‖aH(θ|φ)uM‖2=0

(4)

其中uM是最小特征值λM所对应的特征向量。

此时,经典MUSIC算法中的对到达角的估计伪谱:

(5)

就将被修正为

(6)

从上面的伪谱可以看出,由于原有的搜索是在由M-D个特征向量所构成的区间上进行计算,而一维噪声子空间法相当于只在一个向量上进行运算,所以这种改进型DOA方法被称作一维噪声子空间方法。文献[5,8]等认为,这种方法不仅在一定程度上克服了由于信噪比和采样数限制而产生的“特征值泄露”问题,在计算量上也有了很大改善。

但是,经过反复验证,上述结论并不准确。

3 对一维噪声子空间算法理论局限性的讨论

首先,由“特征值泄露”而导致的噪声特征值分化,并不像文献[5,8]以及其他文献中所提到的那样——只有最小特征值仍接近真实值,全部噪声特征值从大到小排列变为式(6)的形式。大量的计算表明,分化后的M-D个噪声特征值实际上是围绕σ2两侧分布,并且,分化后的噪声特征值的均值接近σ2。也就是说,在递减排列的噪声特征值中,最接近理论值的,并不是最小的噪声特征值,而是居于多个队列中间位置附近的某个特征值;并且,最接近理论特征值的实际值,可能大于也可能小于理论值。这样,就不能简单的仅以最小特征值来判定理论计算值,而需另外的数学手段来确定了,比如,可以先计算小特征值的均值,再寻找最接近此均值的特征值。

其次,在M-D个小特征值中,与其他特征矢量相比,最接近理论值σ2的噪声特征值所对应的特征向量,与当前方向下的阵列流型矢量的正交性并不一定是最好的。一系列计算表明,与阵列流型矢量有着最佳正交性的特征矢量所对应的特征值,在固定的排序中呈现某种随机分布。

从上面的分析可以看到,实际上对一维噪声子空间进行推导的前提并不正确。但是,作为一种富有启发性的思路,仍有借鉴性。

再回头分析一下因受“特征值泄露”影响而不准确的噪声特征值。前面提到过,此时的噪声特征值已经不再“相等且等于噪声的方差”,而是围绕理论上的特征值上下进行分布。相应的,原有的特征向量也会变得不再与阵列流型矢量严格正交。如果按照原有的计算步骤,将噪声子空间与阵列流型正交运算并搜索极值的话,计算偏差显然很大。但是可以发现,虽然“特征值泄露”后每个特征向量都产生了一定的偏差,但是任意单个特征向量的正交性都优于“特征值泄露”后的整个噪声子空间的正交性。也就是说,任选一个特征向量,如最小特征值所对应的特征向量,然后将其替换原有的噪声子空间,所得的结果就应比替换前要好。从这个角度来看,虽然文献[5,8]所述的以为噪声子空间方法的理论基础并不完全正确,但是其对计算结果确实有一定的改善,同时,也确实大大降低了计算量,所以,对于这种应用于DOA中的一维噪声子空间思想,仍可以借鉴。

4 对一维噪声子空间算法应用局限性的讨论

事实上,一维噪声子空间算法除了理论上存在商榷之处外,应用中也有局限性。下面计算采用一维噪声子空间方法时,一个入射信号和两个入射信号的MUSIC谱。以8元均匀直线阵为例,设有两个信号分别从0°和30°方向入射,接收端信噪比为10dB,其MUSIC谱如图1。

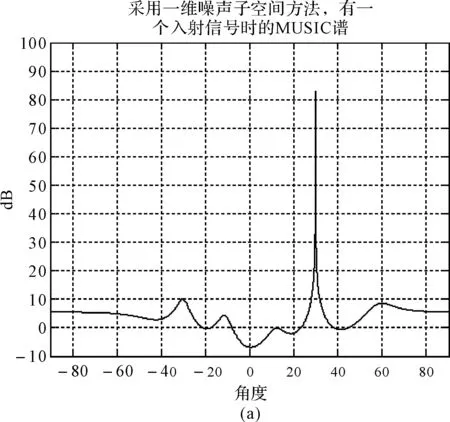
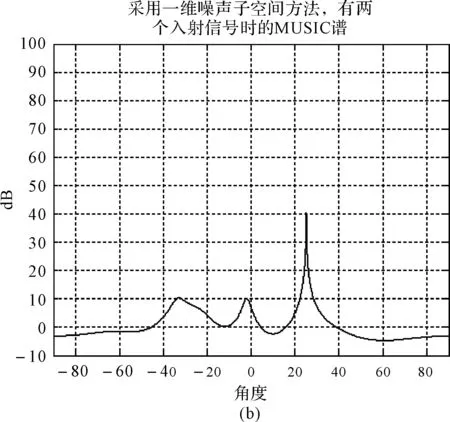
图1 有一个和两个信号入射时的MUSIC谱

图1计算了有一个和两个入射信号时,采用一维噪声子空间计算得到的MUSIC谱。图1(a)可以看出,当有一个入射信号时,可以根据谱峰搜索将来波方向成功的计算出来,所得的伪谱尖锐,且与角度对应比较准确,结果令人满意;但是图1(b)中,当有0°和30°两个入射信号时,虽然在这两个方向出现了峰值,但是没有信号的一个方向-33°附近也出现了一个峰值,而且该峰值比0°方向的峰值更高。从这两个图的对比可以看到,当入射信号超过一个时,谱峰高度可能会低于没有入射信号的方向,此时就会使计算发生错误。

通过观察和分析可以知道,虽然一维噪声子空间能够减小计算量,同时也可以提高MUSIC的谱峰高度,但是在有多个入射信号或者低信噪比的情况下,非期望的峰值可能会高于期望方向的峰值,从而导致计算失败,这是一维噪声子空间方法的应用局限性。

5 结语

论文分析了一种“一维噪声子空间算法”在DOA估计方面的优点和应用局限性,然后DOA结果进行了计算。计算表明,该种改进型自校准算法在只有一个入射波时仍能有效地估计出来波方向,且计算量有了较大的改善,但入射波在某些情况下时,可能会出现计算错误的情况。

[1] Robert J Mailloux.相控阵天线手册[M].北京:电子工业出版社,2007.

[2] 刘鸣,袁超伟,贾宁,等.相控阵天线技术与应用[M].北京:机械工业出版社,2007.

[3] 苏卫民,顾红,倪晋麟.通道失配对MUSIC空间谱及其分辨力的影响[J].电子学报,1998,26(9):142-145.

[4] 王鸿兴.天线阵列自校正算法研究[D].长沙:国防科学技术大学,2006.

[5] 罗利春.基于一维噪声子空间的空间谱估计算法[J].中国空间科学技术,1994(1):1-8.

[6] Haykin S, Reilly J P, Kezys. Some aspects of array[J]. Signal processing, IEEE Proceeds-F,1992,139(1):1-26.

[7] Hill D S. Multiple signal DF using super resolution: a practical assessment. ECEJ, DEC,1990:221-232.

[8] 张浩,张志军,朱国军.采样数据重构的修正一维噪声子空间算法[J].电声技术,2006(11):4-6,11.

[9] 李海鹏.基于空间谱估计的阵列误差校正方法研究[D].西安:西安电子科技大学,2011.

[10] 闵永生,罗景青,吴世龙.基于均匀圆阵的方位估计及互耦自校正算法[J].探测与控制学报,2011,33(6):66-70.

[11] 张志军,张浩,朱国军.阵列幅相误差影响下的一维噪声子空间算法[J].兵工自动化,2006,25(12):45-47.

Limitations of the Application of One-dimensional Noise Subspace Algorithm in DOA

LIU Jianxin

(China Airborne Missile Academy, Luoyang 471009)

The one dimension noise subspace algorithm are discussed. Some mistakes of that algorithm are pointed out, and limitations of that algorithm are studied under different conditions. Conclusion is that although there are limitations on the theory and application, but under certain conditions results of DOA are satisfied, meanwhile the amount of calculation is greatly reduced, so there is still values for that algorithm.

phased array antenna, classic MUSIC algorithm, one-dimensional noise subspace algorithm

2015年6月8日,

2015年7月29日

总装“十二五”高技术支撑项目(编号:6190102503)资助。

刘建新,男,硕士,助理工程师,研究方向:弹载制导数据链等。

TN82

10.3969/j.issn.1672-9730.2015.12.011