基于人工智能的无人机航路设计的浅用*
万业军 李伟兵
(1.武汉军械士官学校 武汉 430208)(2.陆军军官学院 合肥 230031)
基于人工智能的无人机航路设计的浅用*
万业军1李伟兵2
(1.武汉军械士官学校 武汉 430208)(2.陆军军官学院 合肥 230031)
论文在蚁群算法实现人工智能优化的基础上,建立了基于最短路径的风险规避模型。利用数学几何原理对初步方案再优化,得到满足决策者风险要求的最优飞行方案。基于Matlab软件实现了对模型模拟仿真,其计算机模拟计算过程也显示了良好的风险规避效果。
人工智能; 蚁群算法; 航路设计; 无人机
Class Number V279
1 引言
武器无人化的发展趋势成为各国军事力量的一个重要特征,而无人机(UAV)作为武器无人化的杰出代表在现代战争中的作用越来越突出[1]。实现无人机自主飞行的关键问题是无人机的航路设计[2],这个过程中要考虑侦察任务要求、威胁分布、飞行器性能、燃料限制等因素,因此航路设计很大程度上是在满足任务要求的基础上,综合考虑飞行器性能,并规避敌方威胁,找寻最短侦察路径的过程。而在侦察任务量比较大的情况下,一般的优化方法不能满足复杂的模型求解需要,这时通常用人工智能优化方法替代,而蚁群算法是最常用的智能算法之一[3~7]。为了寻找无人机对所有侦察点实现侦察的最优或次优的飞行路线,本文在蚁群算法实现对航路人工智能优化的基础上,考虑敌方威胁分布,提出了基于最短路径的规避风险算法,提高了航路的安全性。
2 基于蚁群算法最优模型的建立
无人机在申领侦察任务包括侦察点数量和地理位置后,假设航路优化设计的目标是巡航距离最短,则可利用人工智能的蚁群算法[6,8]来获得无敌方威胁时的无人机最优航路。
设bi(t)表示t时段位于侦察点i的蚂蚁数目,τij(t)为t时段路径(i,j)上的信息量,n表示侦察点的数量,即该航路设计的规模,m为蚂蚁的总数目,则有
侦察点的集合记为C,设Γ为t时刻集合C中两两侦察点路径上残留的信息素量集合,则有
Γ={τij(t)|ci,cj⊂C}
在初始时刻各条路径上的信息素量相等均为P,则τij(0)=P,而基本蚁群算法的寻优是通过有向图g(C,Γ)来实现的,目的是找寻出长度最短的Hamilton圈。
因蚂蚁k不能重复经过同一侦察点,因此有必要建立一个禁忌表tabuk(k=1,2,…,m)来记录蚂蚁k走过的侦察点,禁忌表随着时间做动态调整。
建立蚂蚁k由i侦察点转移到j侦察点的状态转移概率如下
上式中α为信息启发式因子,表示路径的相对重要性,是对所积累的信息素影响作用的一个加权值;β为期望启发式因子,表示能见度的相对重要性;ηij(t)为启发函数,其表达式为
在一个循环结束后,需对残留信息进行更新处理,故对于t+n时刻给定如下信息量处理规则
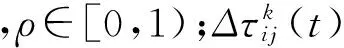
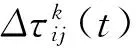
上式中Q表示蚂蚁携带信息素的量,其值的大小影响算法的收敛速度;Lk表示第k只蚂蚁在本次循环中所走路径的总长度。
3 基于最短路径的风险规避模型的建立
假设无人机在巡航空域存在来自敌方的威胁,本文以若干敌方导弹分队为例,设其有效攻击空域为圆面,圆心为O,坐标已知,半径为R,两个毗邻的侦察点为A,B,坐标已知,首先要判断导弹分队是否对无人机带来实际威胁,而后针对实际威胁进行风险规避。
引理 如图1所示,若AB为圆O的割线,若从A点不经过圆面部分到B点,此时最短的路径为
对照图1的几何图形,引理的正确性是显而易见的。
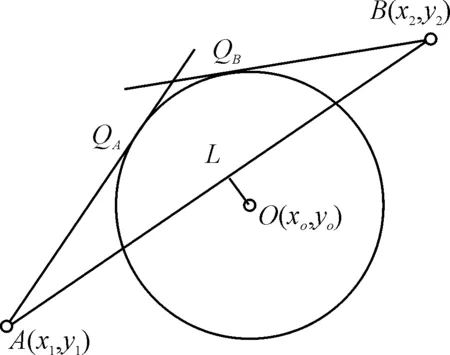
图1 毗邻侦察点、敌方导弹分队示意图
引入参数a,b,c,可得到圆O的割线AB和圆心O到AB的中垂线OL的两点式方程和通用方程,分别设为
AB:ax+by+c=0;OL:a(y-yo)-b(x-xo)=0
根据已知条件可得方程分别为
通过解方程组可得L点的坐标
根据点到直线的距离定理,对于直线来言,圆心O的坐标(xo,yo)到直线的最短距离为
根据待定系数法求出对应的三个未知数a,b,c,略去求解过程可得到三个未知数a,b,c的值分别为
因此可计算出点(xo,yo)距直线的最短距离L,而敌方威胁的个数可根据L与R的关系来判断,用0,1来表征实际威胁,因此判断实际威胁的方法如下
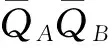
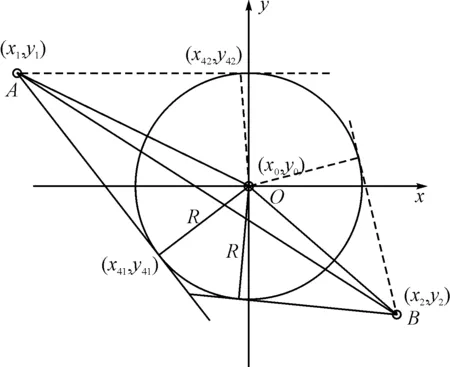
图2 切点坐标算法示意图
线段AQA,QBB的长度的计算方法采用两点间的距离公式直接求解,这要求知道两个切点的坐标,这是本文求解的一个非常重要的环节,具体实施方法,如图2所示。
根据三角函数和反三角函数的知识对两种情况下的切点坐标进行求解,两个切点的表达式分别为
4 程序实现与模拟仿真
本文给出一个航路设计的实例,设无人机起飞点坐标为(0,0),并把它作为航路设计的第一个侦察点,任务侦察点、威胁圆心的经纬度如表1所示。
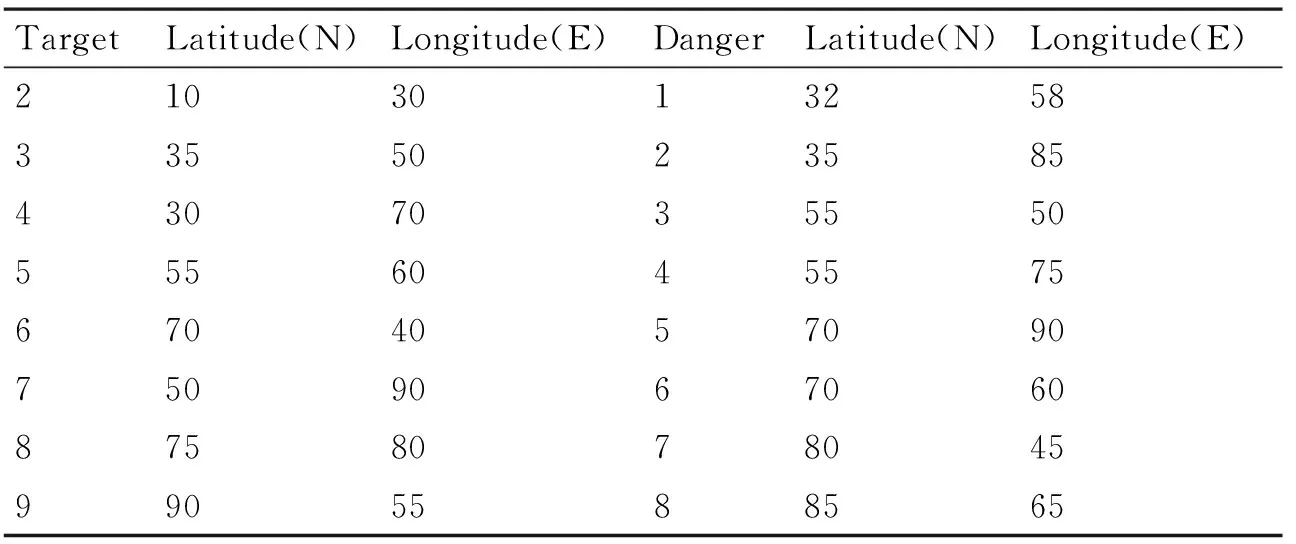
表1 经纬度表
假设地球为球形,则球的表面距离公式为
l=(Re+H)×arccos(sinN1sinN2
+cosN1cosN2cos(E2-E1))
其中Re为地球半径,取Re=6400km,H为某型无人机巡航高度,取H=10km,N1,N2为两点的纬度,E1,E2为两点的经度。
4.1 基于蚁群算法最优模型的模拟
采用Matlab计算软件[9],基于蚁群算法最优模型的求解采用基本蚁群算法[5,8,10]的实现步骤如下:
step1:参数的初始化。时间t=0,循环次数NC,最大循环次数NCmax,初始化信息素量P,初始时刻Δτij(0)=0,蚂蚁数量m,目标点数n;
step2:循环次数Nc随着循环发生而自增:Nc=Nc+1;
step3:初始禁忌表索引号k=1;
step4:蚂蚁的编号随循环而自增k=k+1;
师:孩子们,知道五月份的第二个星期日是什么节日吗?(生:母亲节)我给我的妈妈送了两份礼物。(出示课件:包包326元 丝巾235元)
step5:根据状态转移概率公式计算的概率决定蚂蚁个体选择的目标点j;
step6:将第j个侦察点添加到禁忌表中;
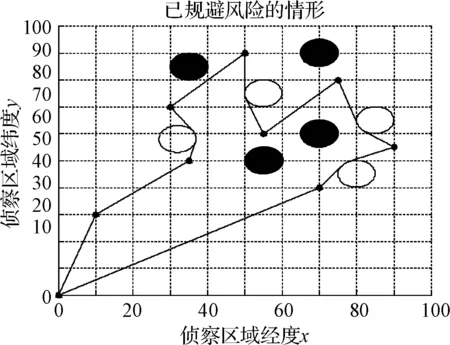
step7:判断集合C中侦察点是否遍历完全,即判断k step8:根据本文第一部分的信息素更新公式更新每条路径上的信息量。 step9:查看循环次数是否满足条件Nc≥NCmax,若是,则结束程序并输出计算结果,否则清空禁忌表并跳转到step2。(结果见图3,黑色圆为敌威胁区域) 图3 基于蚁群算法最优模型的航路 4.2 基于最短路径的规避风险算法的模拟 基于最短路径的风险规避模型的求解步骤如下: step1:规避运算参数的初始化。最优路径Shortest_Route,每段规避排除的最小距离best_distance,导弹火力半径R,每段路径多出的距离bonus; step2:对两两侦察点之间的路径进行判断,观察是否存在威胁的影响,若威胁圆心到路径的距离小于R,且其垂点在路径上,则有影响,反之,危险点到路径的距离大于等于R,无影响; step3:有影响时,规避风险,按照给出的最短路径结论处理,获得新的最小路径,并获得最小距离best_distance,减去两侦察点的距离得到每段路径多出的距离bonus; step4:无影响时,不作处理,依照原路径; step5:循环完毕时,风险规避完毕,威胁得到排除,画出规避后的最优航迹仿真图; step6:输出新的最短路径距离New_Shortest_Length,其值的得到途径为:把sum(bonus)+Shortest_Length即得到。(结果见图4,圆两个切点间的一部分弧线作为航路使用) 图4 基于最短路径的规避风险模型的航路 本文在蚁群算法智能优化的基础上,建立了基于最短路径的风险规避模型,得到了满足决策者风险要求的最优飞行方案,并进行了模拟仿真,显示了良好的规避风险效果,在整体上,满足了无人机航路安全、高效,经济的要求。 本文的威胁区域为导弹分队,实际上,天气带来的风云雨雾区域也是无人机飞行的威胁,且此时的区域不再是规则的圆面,更不规则的区域的情况下,最优的航路也是存在的,求解方法的困难也会提升不少,这也是本文下一步的研究方向。 [1] 钱立志,汪卫华.无人机作战运用[M].北京:解放军出版社,2011. [2] 都基焱.无人机兵器原理[M].北京:解放军出版社,2005. [3] 孙力娟,王良俊,王汝传.改进的蚁群算法及其在TSP中的应用研究[J].通信学报,2004,25(10):111-116. [4] 陈宏建,陈峻,徐晓华,等.改进的增强型蚁群算法[J].计算机工程,2005,31(2):176-178. [5] 孔令军,张兴华,陈建国.基本蚁群算法及其改进[J].北华大学学报(自然科学版),2004,5(6):572-574. [6] 叶文,范洪达.基于改进蚁群算法的飞机低空突防航路规划[J].飞行力学,2004,22(33):35-38. [7] 丁建立,陈增强.遗传算法和蚂蚁算法的融合[J].计算机研究与发展,2003,40(9):1351-1356. [8] Dorigo M,Gambardella L M.Ant colony system: A cooperative learning approach to the traveling salesman problem[J].IEEE Trans.Evolutionary Computation,1997,1(1):53-66. [9] 赵静,但琦.数学建模与数学实验[M].第3版.北京:高等教育出版社,2008. [10] 洪玉振.TSP最短路径的必要条件初探[J].河海大学学报,2006,9(6):717-720. Application of Artificial Intelligence Method in Unmanned Aerial Vehicle’s Route Design WAN Yejun1LI Weibing2 (1.Petty Officer Academy of Armament,Wuhan 430208)(2.Army Officer Academy,Hefei 230031) Based on the artificial intelligent optimization of the ant colony algorithm,an avoid risk model based on the shortest path algorithm is established.Mathematical geometry principle is used let preliminary scheme have second optimization.At last,a optimal flight plan which can satisfy given risk demand is obtained.And based on the Matlab software,Matlab code realizes the writer’s thinking design,and its computer simulation and calculation process also has received the good effect. artificial intelligence,ant colony algorithm,flight route design,UAV 2014年8月3日, 2014年9月27日基金项目:武器装备军内科研项目基金(编号:012043)资助。 万业军,男,助理工程师,研究方向:无人机指挥控制。李伟兵,男,硕士研究生,助理工程师,研究方向:优化理论与方法。 V279 10.3969/j.issn1672-9730.2015.02.018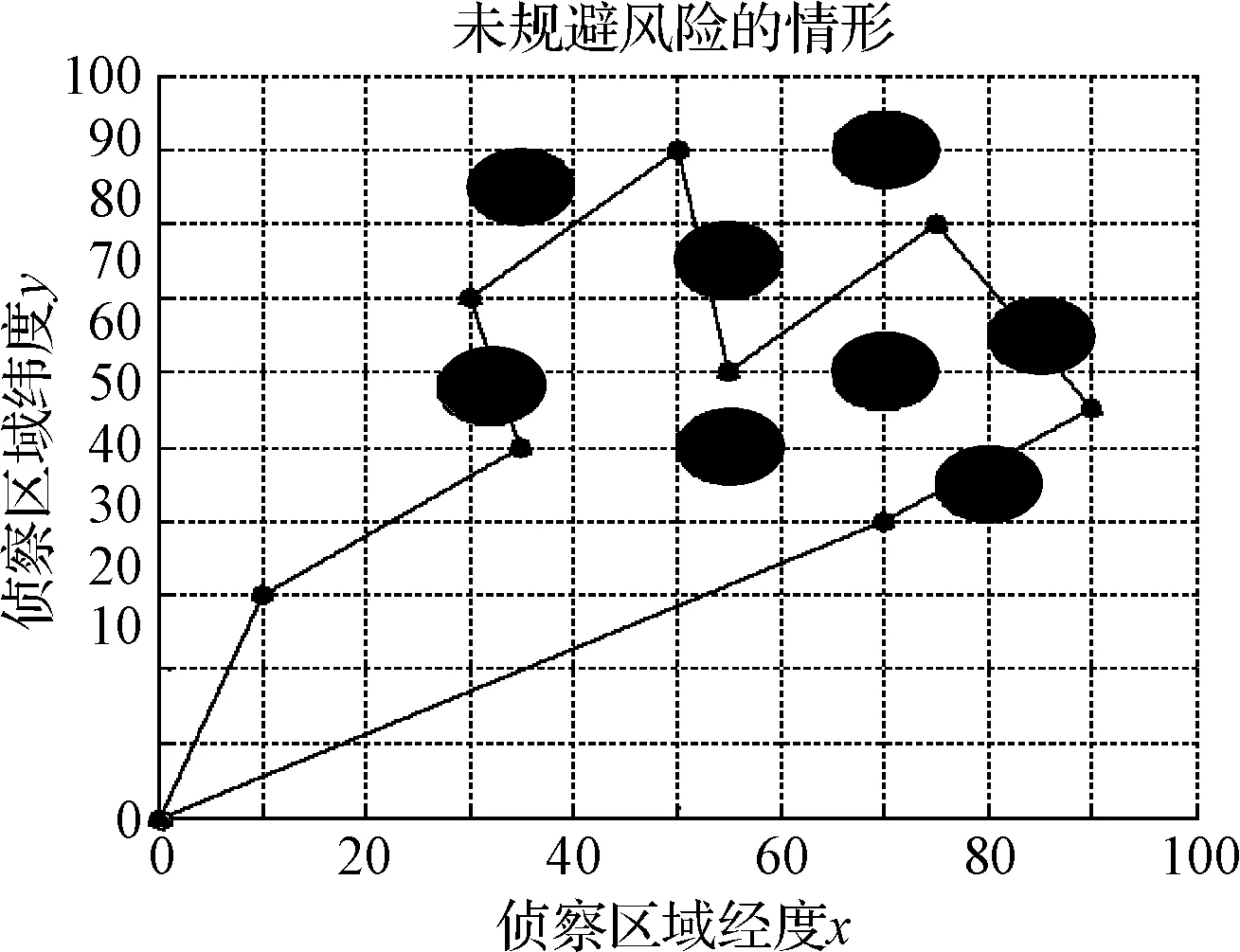
5 结语

