基于二维最大熵法的图像感兴趣区自动提取研究*

魏海永 罗 航

(海装武汉局驻景德镇军事代表室 景德镇 333002)



基于二维最大熵法的图像感兴趣区自动提取研究*

魏海永 罗 航

(海装武汉局驻景德镇军事代表室 景德镇 333002)

论文在传统的二维最大熵图像感兴趣区提取方法的基础上,提出并推导了逐次逼近二维最大熵递推搜索算法,并经实验验证该算法具有较好的实时性,具有一定的工程实践价值。

感兴趣区; 雷达; 作战仿真

Class Number TN911.73

1 引言

为了解决巡逻攻击导弹末制导图像在有限带宽进行传输的问题,需将图像数据(常见的类型包括红外图像、视频图像、雷达图像等)压缩后在有限带宽信道上传输。然而对于此类的图像信息,可能存在目标的区域,是军事应用研究的重点,即图像感兴趣区域(region of inertest,ROI)。如何从复杂战场图像中自动提取感兴趣区,对目标的自动识别及跟踪研究具有重要的实际意义,具有很强的军事研究价值。由于我军数据链建设还只是基本上实现了“互连互通”,带宽窄,还无法实时或近实时地传输末制导序列图像,因此针对单帧图像开展目标感兴趣区自动提取研究具有很强的现实意义。

传统的图像的全局二维熵可以定义[1]为

H(s,t)=H(A)+H(B)

(1)

通过求最大化H(s,t),可以找到最佳的门限(s,t)。由于对于每个(s,t),都要从头开始计算PA和HA,整个运算过程是一个四重循环,算法效率不高。

常用的图像分割方法存在的主要问题是不能对不同大小的目标进行有效分割,或者难以实现分割实时性和分割有效性的统一。Prewitt众数法、OTSU方法等传统阈值方法要求目标大小在30%以上[2],且随着目标相对面积的减小性能随之迅速下降,会产生较为严重的误分割。二维最大熵法虽然能对不同大小目标进行准确分割,但该方法只是简单地将一维寻优推广至二维寻优,导致运算量按指数增长,耗时太长,难以满足实时要求。针对这个现状,人们研究了一些快速算法[3～4],加快了二维最大熵图像分割的速度。本文将在二维最大熵递推优化公式的基础上,提出逐步逼近二维最大熵阈值递推搜索算法,以提升二维最大熵分割的实时性。

2 模型的建立

2.1 二维最大熵递推优化公式

通过求取图像全局二维熵H(s,t)的最大值,就可以找到图像分割的最佳门限(s,t)。然而由式(1)可知,对应每个(s,t),都要从头开始计算PA和HA,运算过程是一个四重循环,计算非常耗时,难以满足应用中的实时需求,因此必须对其进行优化。递推优化公式如下所示:

(2)

=PA(s,t)+PA(s-1,t+1)

-PA(s-1,t)+ps,t+1

(3)

(4)

=HA(s,t)+HA(s-1,t+1)

-HA(s-1,t)-ps-1,tlnps-1,t

(5)

显然,在计算H(s,t+1)时,必须计算PA(s,t+1)和HA(s,t+1),从而就可以递推计算PA(s,t+1)和HA(s,t+1)了。经过递推优化,将二维最大熵的图像阈值分割算法复杂度从O(L4)降到了O(L2)。若想进一步减少运行时间,减少不必要的对数运算和循环次数是提高运行效率的关键。

2.2 逐步逼近二维最大熵递推搜索算法的思想及原理分析

逐步逼近二维最大熵递推搜索算法的基本思想来源于图像多尺度分析的思想,首先在图像粗尺度的二维直方图上搜索出粗略的阈值,然后在这个粗略阈值领域内搜索精确阈值。该算法避免了在不可能存在分割阈值的灰度范围内进行循环和对数运算,提高了该算法的运行效率。

所谓粗尺度的二维直方图,是将原二维直方图一定范围内的元素合并,生成一个尺度更小的二维直方图。

设f(x,y)为一幅二维灰度图像,大小为M*N,其总灰度级为L,G(s,t)为其二维直方图,其定义域为

D={(s,t)|1≤s≤L,1≤t≤L}

(6)

(7)

定义域为

(8)

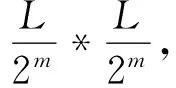
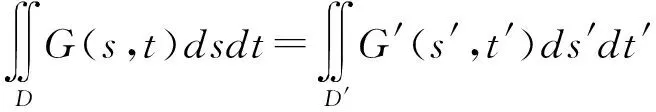
(9)

由于s=2m*s′,t=2m*t′,进行变量代换,G′可用G表示为

G′(s′,t′)=2m*2m*G(2ms′,2mt′)

(10)

可见G′是G经过尺度变换的形式,二者的二维直方图是相似的。在二维直方图中,理论上只有某个点对应的灰度值作为分割阈值时图像的二维熵最大,离该点越远二维熵越小,因此,从G′中能得到阈值的粗略值。

3 递推搜索算法的实现及流程

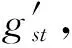
(11)

(12)

(13)

这样就把G′上式(10)～(13)的递推运算转化为PS′、HS′、H′三个矩阵元素的递推计算,找出H′中的最大元素位置就找到了粗略阈值。同样,可以计算出定义在G上的PS,HS和H,设定义域D为

(14)

搜索出粗略阈值后,再在上面的定义域内计算H,这样就可以根据D内H的最大元素位置找到精确阈值,具体流程如图1所示。

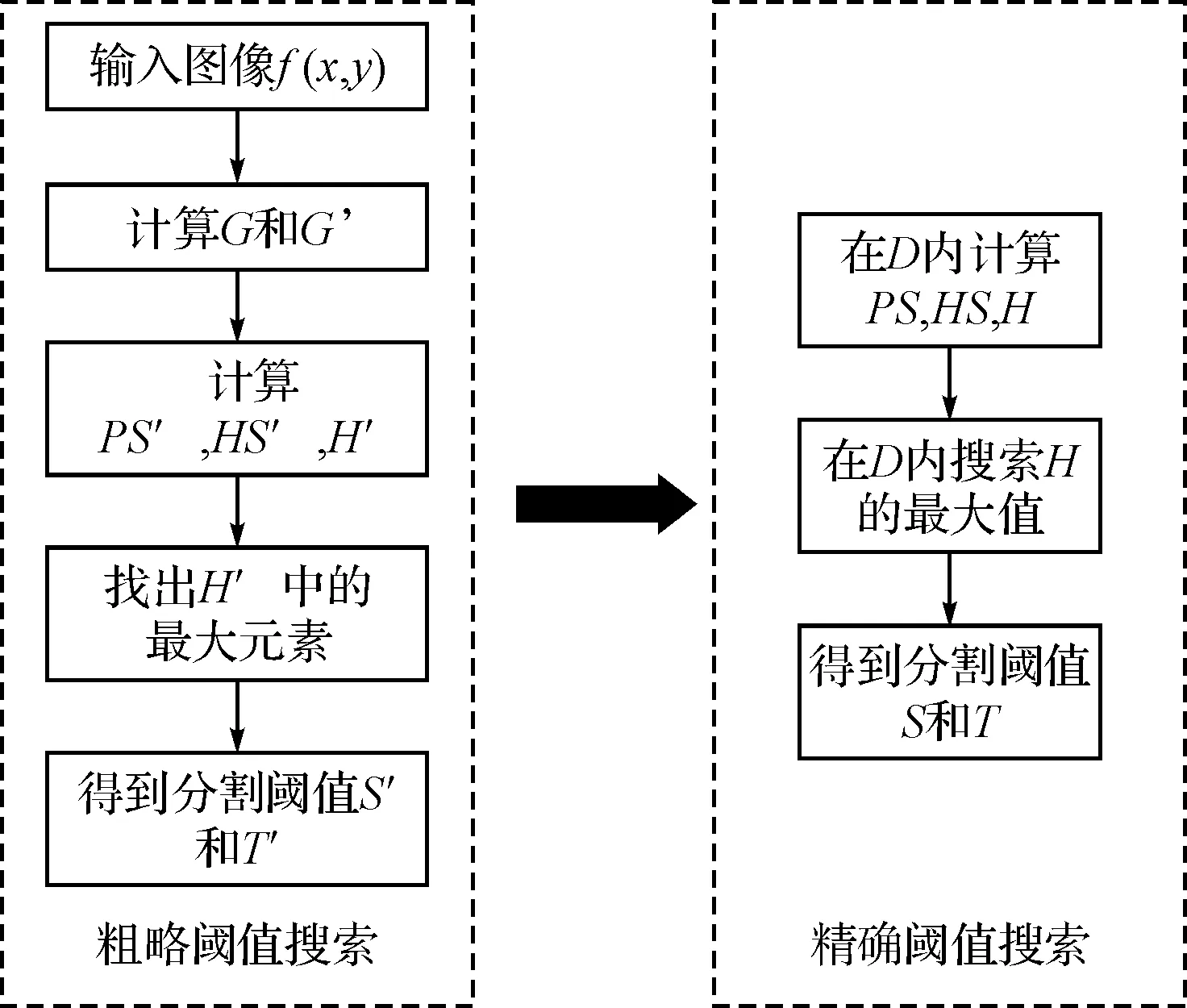
图1 分割阈值搜索流程

使用粗尺度二维直方图进行粗略阈值搜索,可以使用两级搜索,也可以使用多级搜索。与两级搜索相比,使用多级搜索需要更少的循环次数和对数计算次数,但经过对不同图像反复试验得出,由于多级搜索需要更多辅助性的附加运算,两级搜索需要的时间和多级搜索相比差距不是很明显甚至更少,实际上采用了两级搜索,第一次粗搜索的搜索步长为2m=16,若第一次搜索阈值为T,第二次再在[T*16-15,T*16+15]内搜索,达到了较好的效果。

4 图像感兴趣区的提取

相对于背景,感兴趣区域具有相对较多的像素聚集点和相对较好的区域连通性。采用阈值方法对红外目标图像进行分割后得到的是一幅含有目标及离散噪点的二值图像。图像感兴趣区的提取需要综合运用各种技术去除虚警点,恢复目标区域的连通性,增强二值图像的可视效果,最大限度地提取出目标可能存在的区域。主要步骤包括顺序统计滤波、数学形态滤波、矩形感兴趣区域提取。

1) 顺序统计滤波

顺序统计滤波是一种非线性的信号处理方法,m*n邻域内d阶顺序滤波就是取图像中某点的m*n邻域内的点,把它们的灰度值从大到小按顺序排序,选取第d个灰度值作为该点的灰度。m*n邻域内d阶顺序滤波可以表示如式(15):

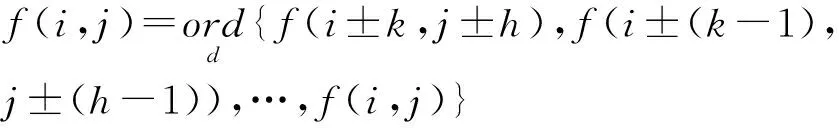
(15)

其中m=2k+1,n=2h+1。将该顺序滤波原理运用于二值图像时,图像只存在两级灰度0和1。当用该像素邻域的灰度中值代替该像素灰度值时,顺序滤波就成为了中值滤波。

在进行图像分割前,可以利用中值滤波对图像进行预处理,它将在一定程度上抑制噪声的影响;分割后得到的二值图像中同时存在着目标点和噪点,这两部分像素点的区别在于其聚集密度不同,可以运用顺序滤波滤除部分离散的噪点,使得在不损失目标信息的同时增强目标像素之间的连通性,减小噪声对目标区域的影响。

2) 数学形态学滤波

数学形态学最早由G.Matheron等在1964年提出,是一种非线性图像处理方法,它建立在几何代数基础上,用集合论方法来定量描述几何结构。数学形态学有四种基本运算:腐蚀(Erosion)、膨胀(Dilation)、开(Open)运算和闭(Close)运算。设f(x,y)是输入的数字图像,定义域为F;g(s,t)是结构元素,定义域为G,则腐蚀和膨胀分别定义为

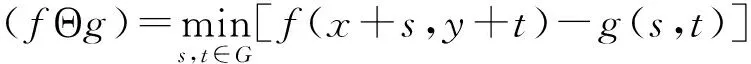
(16)

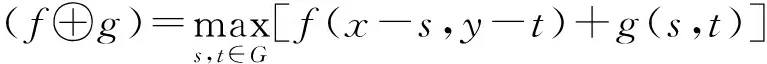
(17)

对结构元素g(s,t)来说,f(x,y)的开运算和闭运算分别定义为

(f∘g)(x,y)=[(fΘg)⊕g](x,y)

(18)

(f·g)(x,y)=[(f⊕g)Θg](x,y)

(19)

顺序滤波后得到的二值图像前景区域同时包含目标区域和聚合噪点区域,采用开-闭的级联操作就可以滤除聚合噪点区域。

3) 矩形区域的提取

由于感兴趣区域的提取主要用于目标人工辅助识别,因此不宜将目标形状直接作为感兴趣区域,因为一旦产生分割错误就会进一步严重影响人的识别效果。在本文中,目标定义为像素数目大于或等于N的连通区域,感兴趣区域定义为包含目标的扩展外接矩形。设B(x,y)为二值图,如图2所示,其宽为W,高为H,建立如图所示的坐标系,设坐标(x,y)是目标target中的点,则xmin≤x≤xmax,ymin≤y≤ymax,则可以定义矩形感兴趣区域为:

ROI={(x,y)|max(xmin,0)≤x≤min(xmax,W),
max(ymin,0)≤y≤min(ymax,H)}

(20)

将上述感兴趣区域的边界向外扩充8个像素得到的矩形感兴趣区为

ROI={(x,y)|max(xmin-8,0)≤x≤min(xmax+8,W),
max(ymin-8,0)≤y≤min(ymax+8,H)}

(21)

图2 感兴趣区域的矩形扩展

在非边界位置时,ROI的最小尺寸为16×16,在边界位置时,以图像的边界为ROI的边界。

5 实验分析

在Pentium Ⅳ 2.4GHz CPU,1GB RAM的计算机上,针对由软件生成的三幅红外图像(大小768*576,如图3所示)进行了图像感兴趣区自动提取实验。其中第一幅红外图像为100m处的坦克,图像中不含噪声,第二幅和第三幅分别为距离3500m和1000m处的舰艇,含有噪声。运用OTSU方法分割效果如图4所示;运用矩不变法分割效果如图5所示;运用逐步逼近二维最大熵递推算法的分割效果如图6所示;经过顺序滤波、数学形态滤波,矩形区域提取之后,感兴趣区自动提取Mask如图7所示。显然,由实验效果来看,OTSU方法能对较大目标进行有效分割,对小目标和或信噪比低的目标分割效果很不理想;矩不变的分割方法对目标大小也非常敏感;本节所提出的逐次逼近二位最大熵递推搜索算法能够对包含不同大小目标且含噪声的红外图像进行有效分割。

图3 红外目标图像

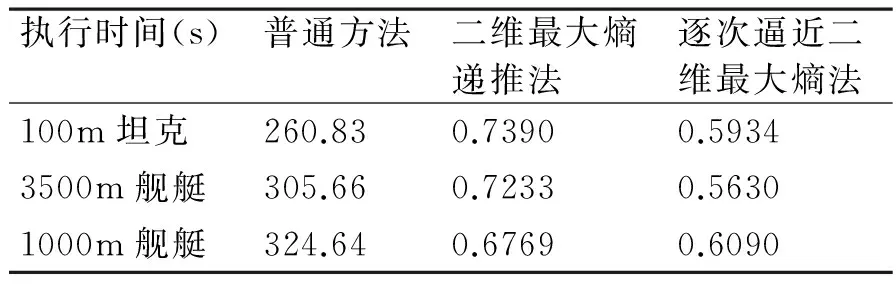
各种方法的图像分割时间如表1所示。逐步逼近二维最大熵阈值递推搜索算法在阈值搜索时间上有了一定的改善,与没有采用任何优化措施的普通算法相比,阈值搜索时间减少了三个数量级,和文献[56]提出的递推方法相比,本文方法的搜索效率也平均提高了17.8%左右。

图4 运用OTSU方法分割效果

图5 运用矩不变方法分割效果

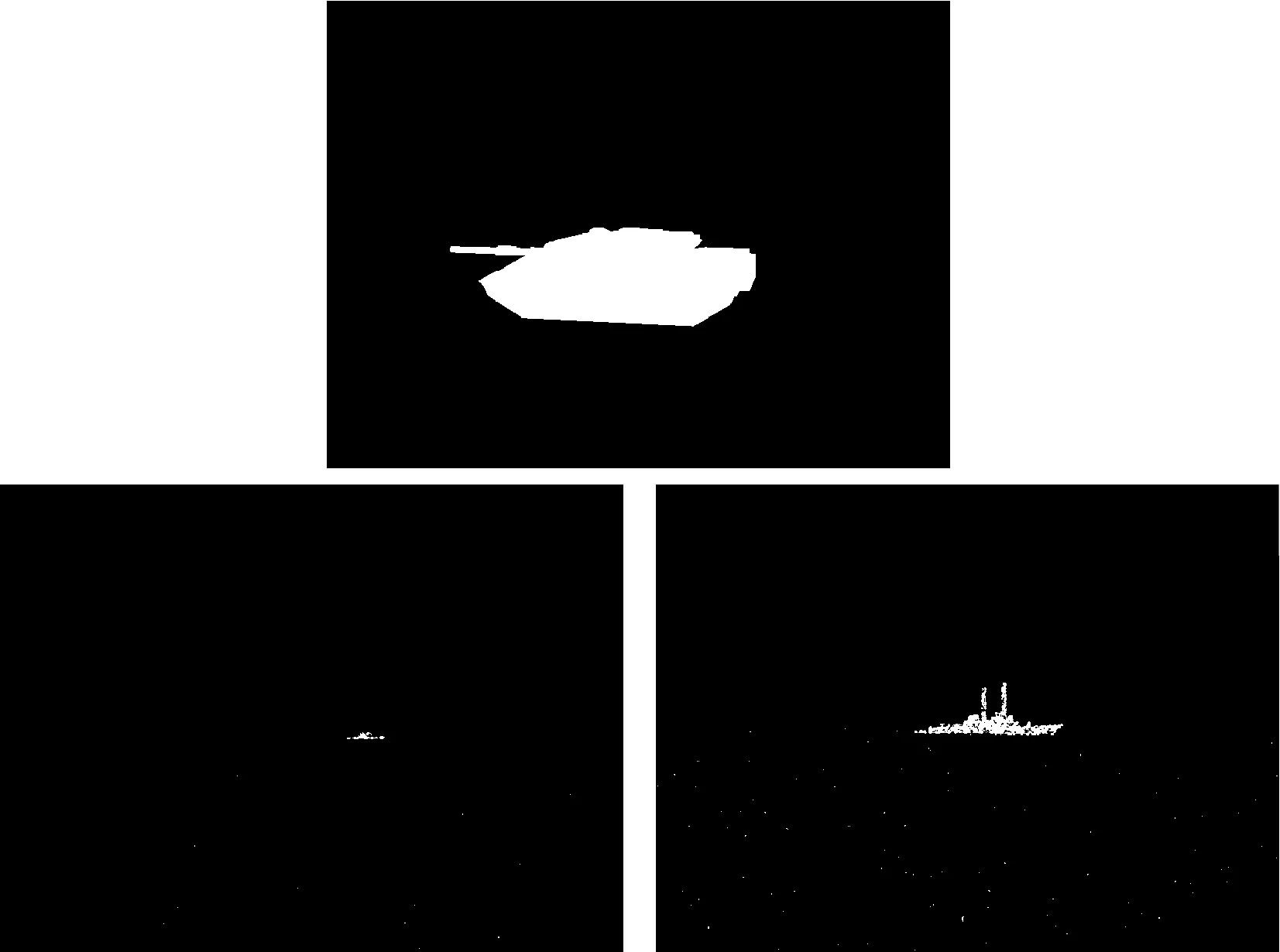
图6 基于逐次逼近二维最大熵搜索算法的分割效果

图7 ROI自动提取的Mask

执行时间(s)普通方法二维最大熵递推法逐次逼近二维最大熵法100m坦克260.830.73900.59343500m舰艇305.660.72330.56301000m舰艇324.640.67690.6090

6 结语

本文在传统的二维最大熵图像感兴趣区提取方法的基础上,提出并推导了逐次逼近二维最大熵递推搜索算法,并经实验验证该算法具有较好的实时性,可用于感兴趣区的自动提取,具有一定的工程实践价值。

[1] Brink A.D.Thresholding of Digital Image Using Two-dimensional Entropics[J].Pattern Recognition,1992,25(8):803-808.

[2] LEE S.U.,CHUANG S.Y.A comparative performance study of several global thresholding techniques for segmentation[J].Computer Vision Graphics and Image Processing,1990,52(3):171-190.

[3] 龚坚,李立源,陈维南.二维熵阈值分割的快速算法[J].东南大学学报,1996,25(4):31-36.

[4] Chen W.T,Wen C.H.A Fast Two-dimensional Entropic Thresholding Algorithm[J].Pattern Recognition,1994,27(7):885-893.

[5] 张纯学.巡逻攻击导弹(LAM)的末制导技术[J].飞航导弹,2006(5):44-47.

[6] 姜百汇,游志成.数据链技术在国外飞航导弹上的应用[C]//发展战略技术创新论文集,2008,5:358-362.

[7] 陈颖,成晓岚.数据链在外军装备中的应用及关键技术[J].航空电子技术,2004,35(4):43-48.

[8] 姜锦锋.红外图像目标检测、识别及跟踪技术研究[D].西安:西北工业大学学位论文,2004:5-10.

[9] 黄柯棣.系统仿真技术[M].长沙:国防科技大学出版社,2004:23-27.

[10] [美]D.K.巴顿.雷达系统分析[M].北京:电子工业出版社,2007:56-58.

Automatic Extaction Based on Recurring Algorithm of Two-dimensional Maximum Entropy Threshold

WEI Haiyong LUO Hang

(Navy Representative Office of Jingdezhen,Jingdezhen 333000)

In this paper,based on the traditional 2-D maximum entropy image interested region extraction method,the approximation 2-D maximum entropy recursive search algorithm is proposed and deduced.Besides,the experiment verifies that the algorithm has good real-time performance and certain value for engineering practice.

region of interest,radar,combat simulation

2014年8月5日,

2014年9月27日

魏海永,男,助理工程师,研究方向:航空机械。罗航,男,助理工程师,研究方向:航空机械。

TN911.73

10.3969/j.issn1672-9730.2015.02.014