基于群组层次分析理论的顾客需求权重确定*

许 诚 王腾飞 王赫巍

(1.海军航空工程学院飞行器工程系 烟台 264001)(2.海军航空工程学院研究生管理大队研四队 烟台 264001)



基于群组层次分析理论的顾客需求权重确定*

许 诚1王腾飞2王赫巍2

(1.海军航空工程学院飞行器工程系 烟台 264001)(2.海军航空工程学院研究生管理大队研四队 烟台 264001)

确定顾客需求权重是质量功能展开(QFD)的关键环节。论文运用群组层次分析法来确定顾客需求权重,首先建立系统递阶层次结构,获取各专家的两两比较判断矩阵,然后对判断矩阵进行一致性检验,并通过相关算法计算得到综合各个专家意见的判断矩阵,最终确定顾客需求权重。最后以潜艇自卫防空武器系统顾客需求权重的确定为例,验证了用群组层次分析法确定顾客需求权重的可行性。

质量功能展开; 顾客需求权重; 群组层次分析法; 一致性检验

Class Number TP301.6

1 引言

质量功能展开(Quality Function Deployment,QFD)技术的分析模型是通过一系列矩阵展开图表的形式,量化分析顾客需求与工程措施之间的关系[1]。QFD技术作为一种事前的策划和系统分析的方法,能够分析和识别“顾客的声音”并将其系统性地转化为工程和管理措施,以实现顾客满意和顾客忠诚为最终目标,将顾客需求、偏好和期望作为整个产品开发过程的关键驱动因素。因此准确的确定顾客需求权重是QFD的关键环节,对QFD的成败有着决定性的作用。

确定顾客需求权重的方法很多,从原理上可以分为功能驱动型、差异驱动型和综合集成型。功能驱动型主要包括集值迭代法、特征值法和基于方案偏好的赋权法,其特点是比较突出地表达评价者主观信息,缺点是对差异的区分不明显;差异驱动型主要包括拉开档次法、逼近理想点法、均方差法和极值法,其特点是突出方案的可辨识性,缺点是会造成一部分评价信息流失;综合集成型主要包括加权求和法、加权秩和法、基于最小二乘支持向量机的方法、模糊综合评判法和群组层次分析法,加权求和法承认各指标对于总目标的贡献是可补偿的,比较容易识别各方面都具有明显优势或劣势的评估对象,但对处于中间地带的评估对象较难识别;加权秩和法结果不会受到原始数据中的极端值的影响,缺点是用“秩”取代了指标的原始值后会造成一部分评价信息的丢失;概率综合系数法[2]主观判断的重要性太大;基于最小二乘支持向量机的方法[3]需要大量数据的支持;模糊综合评判法[4～7]适用性较差,主要适用于评价对象有模糊概念而又可以量化的场合;群组分析法[8～10]能够综合多个专家意见,有助于获得一个合理的综合结果,是一个较为理想的确定顾客需求的方法,下面对群组分析法进行分析研究。

2 群组层次分析法基本原理

2.1 建立系统的递阶层次结构

1) 最高层。这一层次中只有一个要素,一般它是分析问题的预定目标或期望实现的理想结果,是系统评价的最高准则,因此也称目的或总目标层。

2) 中间层。这一层次包括了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需考虑的准则、子准则等,因此也称为准则层。

3) 最底层。表示为实现目标可供选择的各种方案、措施等。

2.2 构造两两比较判断矩阵

设共有k个专家参与顾客权重系数的确定。设在某个准则下第k个专家认为第i个顾客要求相对于第j个顾客要求的相对重要性为aij(i,j=1,2,…,m;k=1,2,…,k),则共给出如下的k个判断矩阵:

2) 计算一致性指标C.I.

式中,(AW)i表示向量AW的第i个分量。

R.I.(Random Index)是同阶随机判断矩阵的一致性指标的平均值,其引入可在一定程度上克服一致性判断指标随n增大而明显增大的弊端[11],通过查找相应的平均随机一致性指标R.I.可得R.I.的值。表1给出了1～14阶正互反矩阵计算1000次得到的平均随机一致性指标。

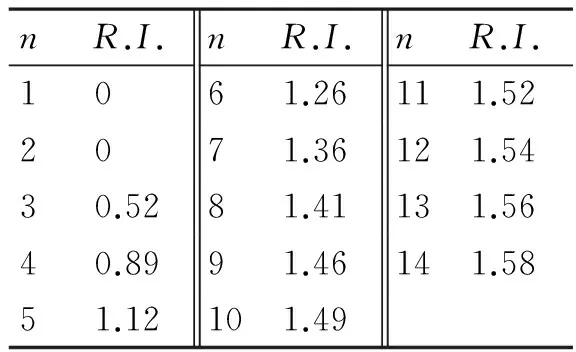
表1 平均随机一致性指标

2.3 综合分析各专家意见

当专家给出的判断矩阵一致性较差,对某两个顾客要求相对重要性的判断差距较大时,将无法通过一致性检验,就需要由专家对其重新协商和判断。当所有的Ai和Aj的相对重要性系数都给定后,就将专家的意见按下述方法进行综合:

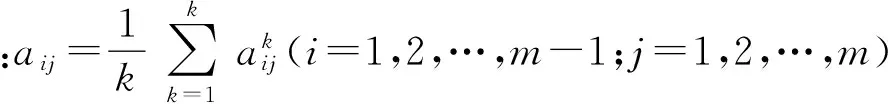
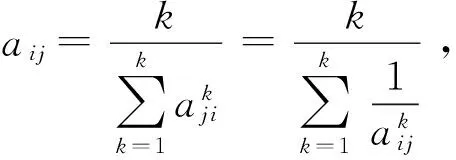
3) 当i=j时,取aij=1。

得到了综合k个专家的判断矩阵,解出其最大特征值λmax及其对应的特征向量ω=(ω1,ω2,…,ωm),并进行归一化处理,得到顾客需求权重ϖ=(ϖ1,ϖ2,…,ϖm),最后进行一致性判断,如不一致,则重复上述过程。

3 应用举例

3.1 建立系统的递阶层次结构

为验证群组层次分析法在确定顾客需求权重中有效性和可行性,下面以某型系统的顾客需求权重确定为例进行说明。

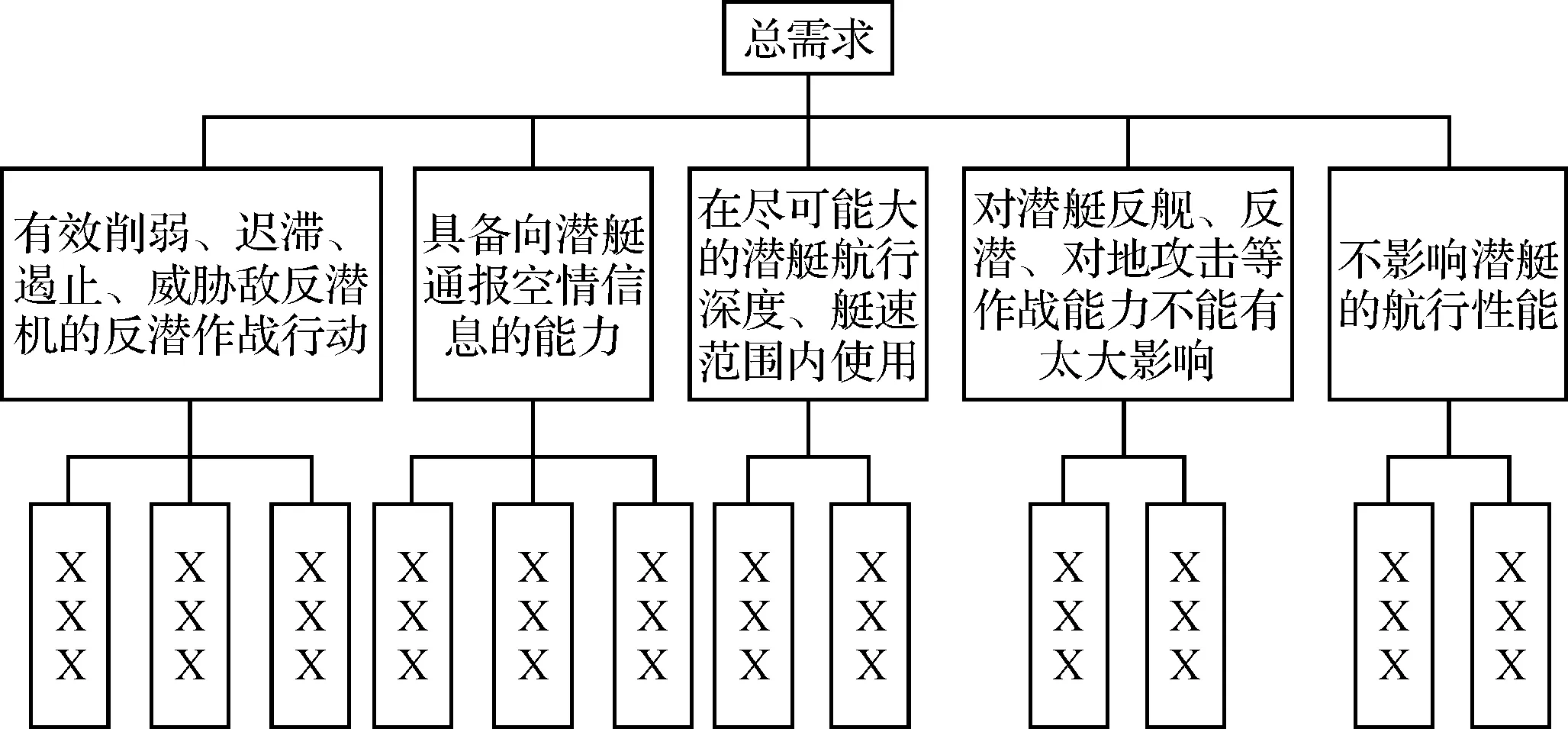
图1 某型系统顾客需求层次结构图

图1为某型系统的顾客需求层次结构图,由于第二层需求与第三层需求计算过程相同,本文仅以第二层次为例进行进算分析,第三层不再赘述。

3.2 构造两两比较判断矩阵

选取三名专家按照表2判断矩阵标度对各顾客需求进行两两比较,并给出判断矩阵。

为方便判断矩阵的表述,对各顾客需求进行如下表述:

表2 判断矩阵标度含义

A1有效削弱、迟滞、遏止、威胁敌反潜机的反潜作战行动;A2具备向潜艇通报空情信息的能力;A3在尽可能大的潜艇航行深度、艇速范围内使用;A4对潜艇反舰、反潜、对地攻击等作战能力不能有太大影响;A5不影响潜艇的航行性能。

各专家权重评分及其一致性检验表3～表7所示。

表3 第一位专家判断矩阵

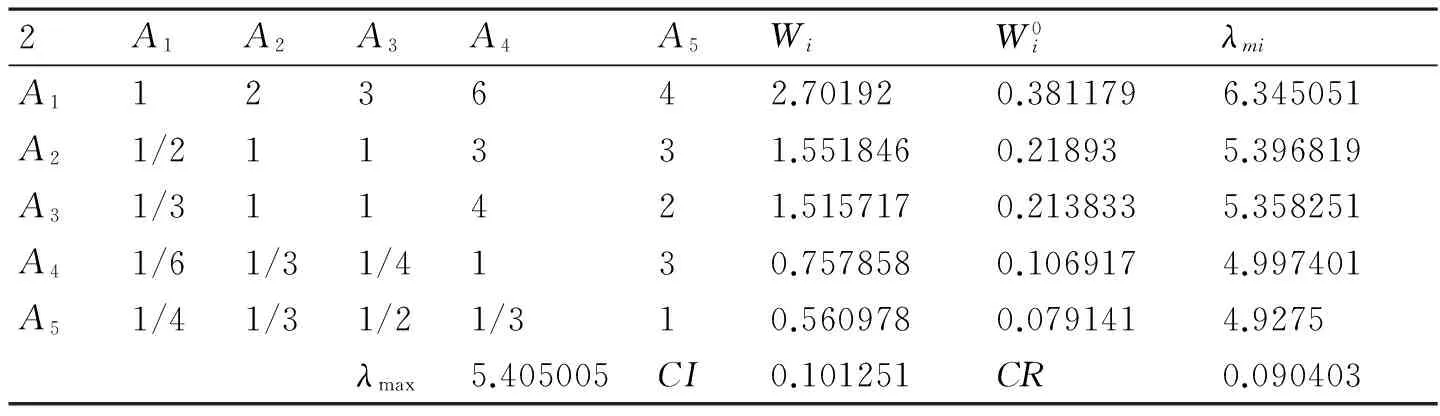
表4 第二位专家判断矩阵

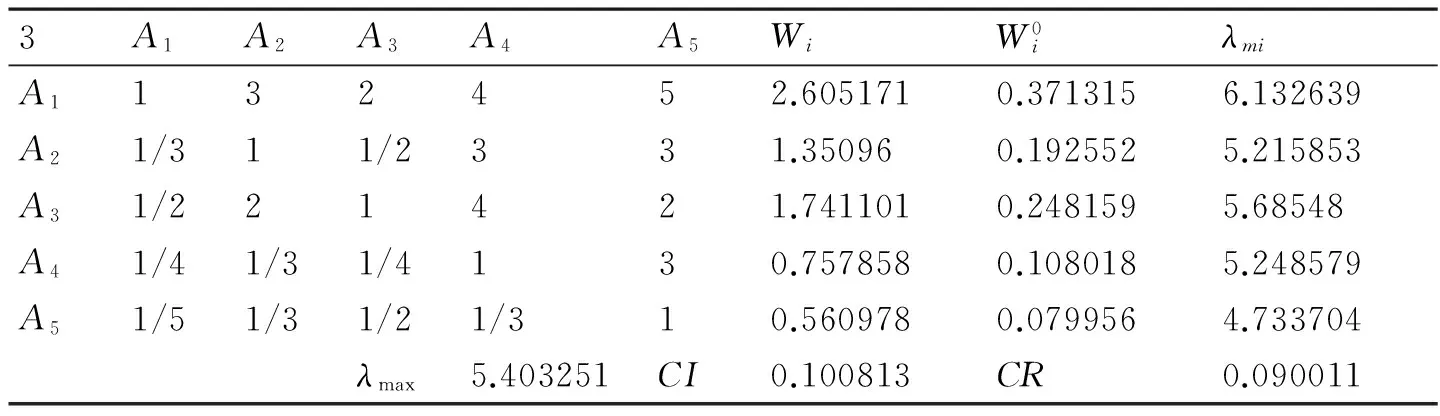
表5 第三位专家判断矩阵

对专家打分进行一致性检验,经计算,其CR值均小于0.1,通过一致性检验,认为其打分具有有效性。

3.3 将专家意见按2.3所述方法进行综合:

经计算,得到了三个专家意见综合判断矩阵。

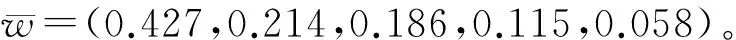
从以上各项权重值可以得到这样的信息:第二层的顾客需求重要度从大到小依次为:有效削弱、迟滞、遏止、威胁敌反潜机的反潜作战行动;具备向潜艇通报空情信息的能力;在尽可能大的潜艇航行深度、艇速范围内使用;对潜艇反舰、反潜、对地攻击等作战能力不能有太大影响;不影响潜艇的航行性能。

表6 专家意见综合判断矩阵

4 结语

群组层次分析方法通过一致性检验分析,保证了专家意见的可靠性,消除了专家评判之间的明显差别;通过分析两两判断矩阵,使顾客需求定量化;通过对各专家判断矩阵的运算,充分综合了各专家的意见。因此,与其他权重分析方法相比,运用群组层次分析方法来确定QFD中顾客需求权重能够综合多个专家意见,有助于获得一个合理的综合结果,是一个较为理想的确定顾客需求的方法。

[1] 李跃生,邵家骏,苗宇涛.质量功能展开[M].北京:国防工业出版社,2011:11-24.

[2] 孔造杰,郝永敬.用权重概率综合系数法确定QFD中用户要求重要性[J].计算机集成制造系统,2001,7(2):65-67.

[3] 陆佳圆,谭建荣,冯毅雄,等.基于最小二乘支持向量机的QFD技术特性权重预测[J].机械设计,2011,28(7):1-7.

[4] 吴永明,罗百祥.绿色质量机能展开中工程特征权重的计算方法[J].计算机辅助设计与图形学学报,2010,22(11):1978-1983.

[5] 刘金林,曾凡明.基于模糊AHP的舰船动力装置需求指标权重计算方法[J].大连海事大学学报,2010,38(4):35-38.

[6] 龚艳萍,赵志刚.用模糊层次分析法确定QFD中消费者要求权重[J].价值工程,2006(7):81-83.

[7] 王琦,钟毓宁.基于模糊层次分析法的QFD顾客需求权重求法[J].湖北工学院学报,2004,19(2):54-57.

[8] 张忠,方可,杨明.基于群组AHP的复杂仿真系统可信度评估方法[J].系统工程与电子技术,2011,33(11):2569-2572.

[9] 曹静,谢武.基于群组层次分析法的广告代理商模糊评价[J].产业与科技论坛,2007,6(7):145-146.

[10] 丁静,张士云,赵静.基于群组层次分析法的配送绩效评价的研究[J].技术经济,2007,26(6):24-27.

[11] 汪应洛.系统工程[M].北京:机械工业出版社,2012:124-126.

Weightiness Confirmation of Customer Requirements Based on Group Analytic Hierarchy Process

XU Cheng1WANG Tengfei2WANG Hewei2

(1.Department of Airborne Vehicle Engineering,Naval Aeronautical & Astronautical University,Yantai 264001)(2.The 4th Team of Postgraduate Management Brigade,Naval Aeronautical & Astronautical University,Yantai 264001)

Determining weightiness of customer requirements is the key link of quality function deployment(QFD).This paper determines weightiness of customer requirements through group analytic hierarchy process.Firstly,the paper establishes a system class hierarchy,gets paired-comparisons judgment matrix of each expert,then tests the consistency of judgment matrix and get the judgment matrix that composite opinion of all experts through the correlation algorithm calculated,eventually determines weightiness of customer requirements.Finally the paper takes weightiness of customer requirements of submarine self-defense air defense weapon system as example,which verifies the feasibility that group analytic hierarchy process can determine weightiness of customer requirements.

QFD,weightiness of customer requirements,group analytic hierarchy process,test the consistency of judgment matrix

2014年8月5日,

2014年9月27日基金项目:海军航空工程学院研究生创新基金资助。

许诚,男,教授,研究方向:导弹武器系统工程。王腾飞,男,硕士,研究方向:军事系统决策。王赫巍,男,硕士,研究方向:军事系统决策。

TP301.6

10.3969/j.issn1672-9730.2015.02.013