基于USQUE的四元数容积卡尔曼滤波算法在组合导航中的应用*

张正彬

(海军驻昆明地区军事代表办事处鱼水雷室 昆明 650000)



基于USQUE的四元数容积卡尔曼滤波算法在组合导航中的应用*

张正彬

(海军驻昆明地区军事代表办事处鱼水雷室 昆明 650000)

组合导航是导航领域中一个重要的研究领域和应用方向。传统的基于惯导误差模型的组合导航模式,因模型在建立过程存在各种近似计算,这必然使得建立的模型中引入诸多近似误差和模型误差,因此,其信息融合的估计精度下降。论文基于USQUE计算流程,提出一种四元数容积卡尔曼滤波算法,并将该算法应用于SINS/GPS位置松组合导航问题当中,仿真结果验证该算法的有效性并且具有较高的估计精度。

组合导航; 卡尔曼滤波; 四元数; USQUE

Class Number U666.11

1 引言

组合导航是导航领域中最为重要的研究分支,并已经成为目前导航领域的研究热点和重要应用方向[1]。组合导航是现代滤波技术和信息融合理论的应用延伸,在组合导航中,相对于位置信息和速度信息,姿态信息的估计尤为重要,这是由于对于经典的SINS/GPS组合导航来说,高精度的位置信息和速度信息都可以通过高精度的外界组合设备获得,而目前来说,对于姿态信息,无法直接有外部组合设备获得,并且又由于该信息在惯导模型中往往耦合在速度信息当中,构成非线性的系统估计方程,因此,也无法直接通过经典的卡尔曼滤波(Kalman Filter,KF)来进行估计[2]。对此,学者们提出基于惯导误差模型的组合导航模型,惯导误差模型是基于惯导解算模型,并通过各种约定近似计算和部分解耦而获得的,而这必然会引入近似误差和模型误差,造成估计精度的下降。

对此,Crassidis等学者提出了一种无味四元数估计方法(UnScented Quaternion Estimator,USQUE)[3～4],该算法在无味卡尔曼滤波(Unscented Kalman Filter,UKF)基础上,利用修正罗格里德斯参数(MRP)搭建桥梁,成功将该算法应用到组合导航领域。USQUE算法的一个重要特点是对于滤波估计来说,其系统方程是基于惯导解算方程的,因此,这就避免了基于惯导误差方程带来的诸多问题。本文提出一种基于USQUE的四元数平方根容积卡尔曼滤波算法(Square-root Quaternion Cubature Kalman Filter,SR-QCKF),利用USQUE在组合导航中应用框架,并结合平方根容积卡尔曼滤波的状态高维估计和数值计算的稳定性等特点,将该算法应用于SINS/GPS位置松组合导航仿真系统当中,仿真结果验证了,该算法的有效性,并具有较高的估计精度。

2 USQUE算法

考虑一个非线性离散系统模型如下

(1)

xk∈in,yk∈im,f(·)和h(·)分别为系统的状态函数与量测函数,qk-1和vk分别为零均值的系统状态白噪声和零均值的系统观测白噪声,即qk-1:N(0,Qk-1),vk:N(0,Rk)。

Crassidis等学者提出了一种USQUE的估计方法巧妙地解决了困扰四元数在非线性滤波当中应用的问题,以下给出USQUE算法的计算流程。

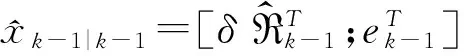
(2)

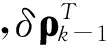
时间更新:

δq0,k-1(i)=

(3)

(4)

根据乘性四元数公式得到

(5)

为了计算一步预测状态及状态滤波方差,根据乘性四元数公式有

(6)

(7)

+Qk-1

(8)

量测更新:

(9)

+Rk

(10)

(11)

Kk=Pxy,k|k-1(Pyy,k|k-1)-1

(12)

(13)

Pk|k=Pk|k-1-KkPyy,k|k-1KkT

(14)

其中yk表示k时刻的观测量。

姿态更新:

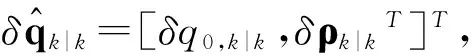
(15)

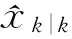
3 基于USQUE的四元数容积卡尔曼滤波算法

平方根容积卡尔曼滤波算法(SRCKF)是容积卡尔曼滤波算法(CKF)的平方根滤波形式,在该算法中不是用滤波方差进行传递,而是用滤波方差的平方根形式进行传递的。因此,其Sigma点采样方式和权重计算为[5～6]

(16)

(17)

(18)

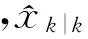
因此,基于这种采样方式给出基于USQUE的平方根容积卡尔曼滤波算法流程如下

时间更新:

(19)

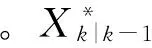
i=1,2,…,2n

(20)

量测更新:

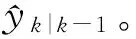
Syy,k|k-1=Tria([Yk|k-1,SR,k])

(21)

(22)

其中SR,k是Rk的平方根形式,Xk|k-1和Yk|k-1表示为

(23a)

(23b)

(24)

(25)

Sk|k=Tria([Xk|k-1-KkYk|k-1,KkSR,k])

(26)

姿态更新:姿态更新同USQUE的算法相同,这里不再赘述。

4 仿真试验

本文将该算法应用于SINS/GPS组合导航当中进行仿真计算,首先给出SINS/GPS组合导航系统方程和量测方程如下所示[2]。

(27a)

(27b)

(27c)

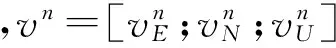
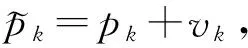
通过仿真一段组合导航轨迹如图1所示。

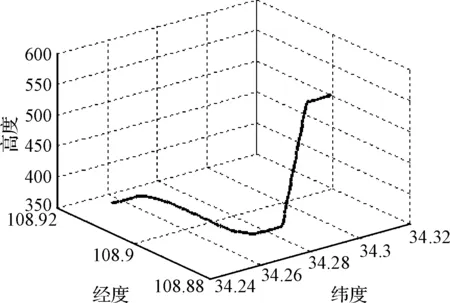
图1 组合导航仿真轨迹

应用该算法分别对姿态、速度及位置信息进行估计,其估计结果如图2～图4所示。

图2～图4表示SR-QCKF对于仿真轨迹姿态、速度和位置估计的误差,从图中可以发现该算法可以将稳态时的姿态估计误差控制在几个角分以内,速度估计误差控制在1m/s以内,位置误差控制在大约1m以内,这个结果对于组合导航来说是估计精度很高的,因此,这也验证了该算法的有效性,为了更直接说明估计效果,给出估计轨迹图如图5所示。

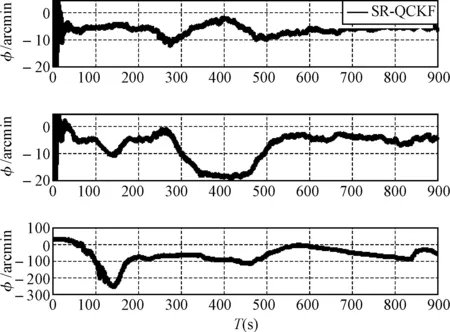
图2 姿态估计误差

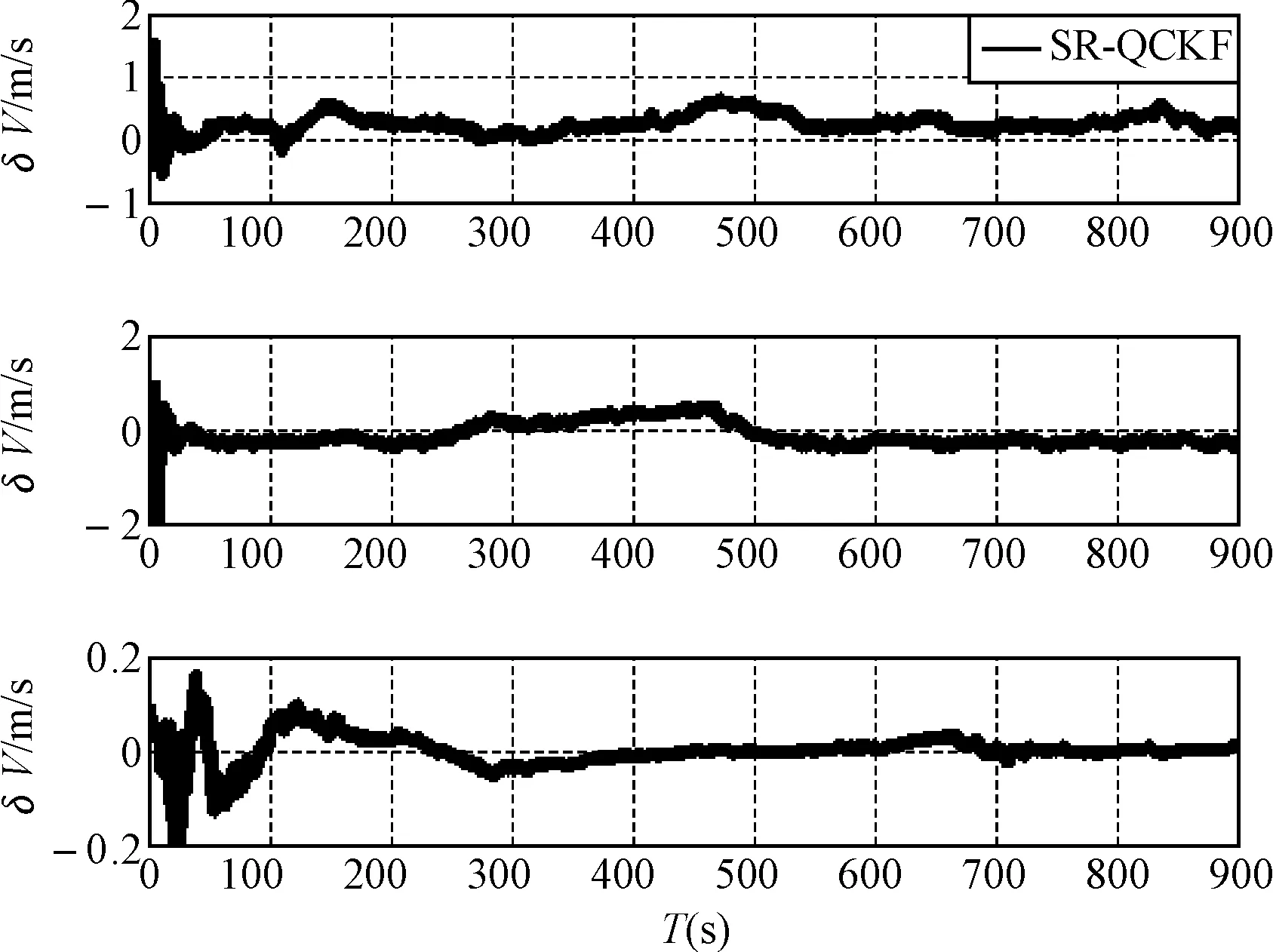
图3 速度估计误差

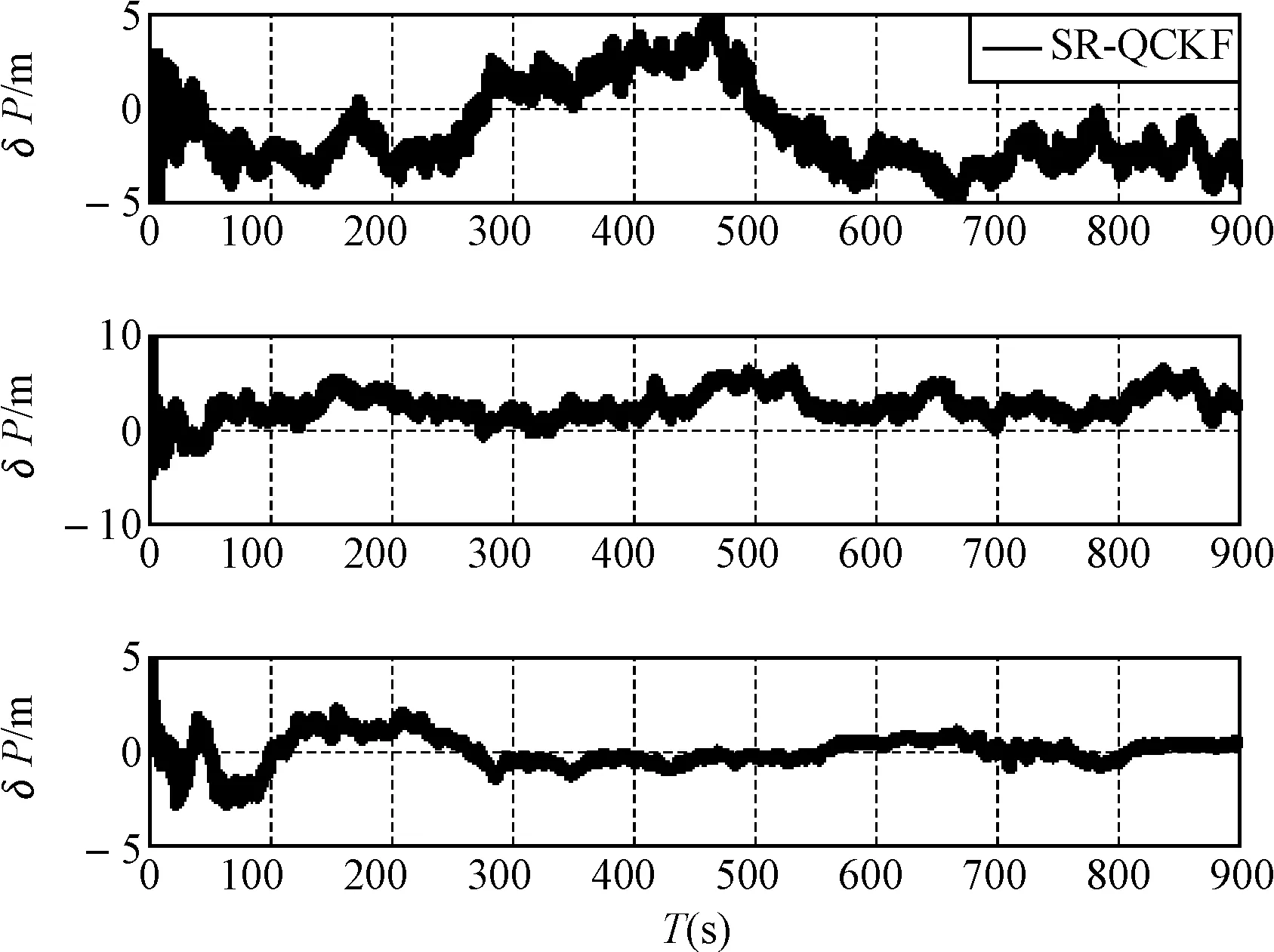
图4 位置估计误差

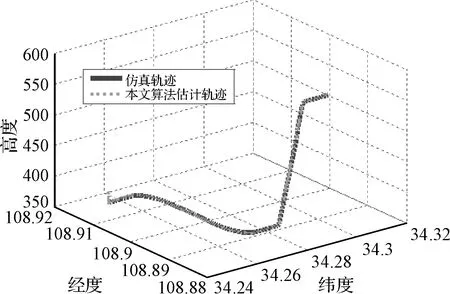
图5 估计轨迹比较

5 结语

本文研究了一种应用于惯导解算方程的直接式组合导航算法,基于USQUE算法的基础上,结合平方根容积卡尔曼滤波算法的特点,提出四元数平方根容积卡尔曼滤波算法,并通过应用在SINS/GPS组合导航当中进行仿真验证,仿真结果验证了该算法的有效性。然而,值得注意得是,由于利用了USQUE算法的框架,本文提出的算法在计算量上会比较大,因此,为了更好地能够将该算法应用于实际,有必要进一步对降低计算量进行研究。

[1] 秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社.

[2] 秦永元.惯性导航[M].北京:科学出版社,2006.

[3] Crassidis J.L.,Markley F.L.Attitude Estimation Using Modified Rodrigues Parameters[C]//Proceedings of the Flight Mechanices/Estimation Theory Symposium,(NASA/CP-1996-3333) NASA-Goddard Space Flight Center,Greenbelt,MD,1996,:71-83.

[4] Crassidis J.C.,Markley F.L.Unscented Filtering for Spacecraft Attitude Estimation[J].Journal of Guidance,Control,and Dynamics,2003,26(4):536-542.

[5] Arasaratnam,I.Cubature Kalman filtering: theory & applications[D].Canada: Diss.Ph.D.Thesis,Department of Electrical & Computer Eng.,McMaster University,2009.

[6] Arasaratnam,I.,Haykin,S.Cubature kalman filters.Automatic Control[J].IEEE Transactions on,2009,54(6):1254-1269.

Application of Quaternion Cubature Kalman Filter Based on USQUE in Integrated SINS/GPS

ZHANG Zhengbin

(Torpedo and Mine Military Representatives Office of Navy in Kunming,Kunming 650000)

Integrated navigation is an important research field and application of navigation field.Because there are a variety of approximate calculation in the establishing process,the traditional model based on the inertial navigation error model is involved with many approximation error and model error,leading to the decrease of information fusion’s estimation accuracy.Based on the USQUE,a quaternion cubature Kalman filter is proposed,which is applied in SINS/GPS located integrated navigation.The simulation results verify the effectiveness and high estimation accuracy of the algorithm.

integrated navigation,Kalman filter,quaternion,USQUE

2014年8月12日,

2014年9月22日

张正彬,男,硕士,助理工程师,研究方向:鱼水雷维修及姿态估计等。

U666.11

10.3969/j.issn1672-9730.2015.02.017