基于PSO_GA算法BPA到PSASP数据转换

叶青，朱永强，李红贤

(华北电力大学电气与电子工程学院，北京市 102206)



基于PSO_GA算法BPA到PSASP数据转换

叶青，朱永强，李红贤

(华北电力大学电气与电子工程学院，北京市 102206)

现存电力系统各商业软件的数据格式不统一，造成了大量异构数据源的存在，仿真软件间的数据交互困难。为解决该问题，提出基于PSO_GA算法电力系统仿真软件BPA到PSASP数据转换的方法，通过分析BPA、PSASP仿真软件中元件模型、控制模型的差异性，建立对应模型间的转换关系以及智能优化算法(PSO_GA)的目标函数及相关约束。利用PSO_GA混合优化算法修正目标转换软件中各模型的参数值，以实现电力系统仿真软件BPA到PSASP数据转换。通过IEEE 43节点的系统算例对BPA向PSASP数据转换过程进行了验证，证明了该方法对电力系统仿真软件数据转换的有效性，并能提高数据转换的准确度和算法的运行速度。

遗传算法；粒子群算法；BPA；PSASP；模型转换；数据转换

0 引 言

随着计算机网络的快速发展，为充分利用电力系统各商业软件已有的数据资源，需要实现不同软件间的数据交互功能。然而，电力系统仿真软件数据格式的设计私有化，造成在不同软件间存在着大量的异构数据源，影响电网工作人员在电力系统规划、设计和运行中做出正确决策。针对上述问题，学者纷纷提出了自己的解决方法。文献[1]基于图论关联矩阵、深度优先搜索等理论，完成了BPA的电网数据向PSCAD/EMTDC 模型的自动转换；文献[2]通过对BPA 与 PSS/E 的潮流数据和暂态稳定模型进行分析和比较，解决了BPA 向 PSS/E数据转换问题；文献[3]分析了PSASP程序与PSS/E 程序的暂态稳定计算数学模型，并通过仿真计算比较了2个程序的潮流计算结果和暂态稳定计算结果。上述方法虽都能实现电力系统仿真软件数据交互的功能，其数据转换的准确度并不高，当出现数据不正确转换时，通常需要进行人工修正参数，增加时间消耗。

近年来，基于群体和适配概念的智能优化算法得到了广泛应用[4-7]，但目前国内基于此类智能算法的电力系统仿真软件间数据转换的研究较少。遗传算法、粒子群算法被广泛应用于电力系统优化配置、参数辨识等问题的求解。文献[5-14]应用遗传算法及算法的改进解决了含有非线性环节的发电机励磁系统、稳定器模型参数不能有效辨识的问题，应用具有自定义建模功能的仿真软件，通过参数辨识程序，实现了实际励磁系统向标准模型转换的参数辨识过程。文献[15-16]应用粒子群算法解决了电力系统无功优化、负荷参数辨识问题，提高了优化过程算法的运行效率和准确性。

众所周知，遗传算法的全局搜索能力强但在搜索最优解时易出现“早熟”现象，且搜索速度慢；而粒子群算法虽然搜索速度快、效率高，算法简单，其缺点是对于离散的优化问题处理不佳，容易陷入局部最优。故此，本文综合遗传算法和粒子群算法的优缺点，提出基于PSO_GA算法解决BPA到PSASP数据转换的智能化方法，以提高数据转换的准确度。通过IEEE 43节点的系统算例对BPA向PSASP数据转换过程进行验证，证明该方法对电力系统仿真软件数据转换的有效性，并能提高数据转换的准确度和算法的运行速度。

1 PSO和GA算法概述

1.1 粒子群算法

粒子群算法(particle swarm optimization algorithm，PSO)是在研究鸟类群体行为的基础上提出的一种智能优化算法，其核心思想是模拟鸟类飞行觅食行为，通过鸟群个体协作使群体得到最优解。粒子群算法具有计算简单、收敛快、鲁棒性好的特点，在最优问题求解方面具有较好的应用。

已知可行解空间的维数为D，群体中粒子数为N，粒子i是一个D维向量xi= (xi1，xi2，…，xiD) (i=1，2，…，n)。每个粒子xi均可能是某个最优问题的可行解，适应度函数f(x)是衡量粒子xi作为可行解优劣的标准。设粒子i飞行速度为vi=(vi1，vi2，…，viD)，第i个粒子目前搜索到的最优位置pid=(pi1，pi2，…，piD)，整个粒子群体目前搜索到的最优位置为pgd=(pg1，pg2，…，pgD)，则粒子速度和位置进行迭代的计算式如下：

(1)

(2)

式中:c1、c2分别为学习因子和非负加速因子，rand(1)是在区间[0，1]中均匀分布的随机数，粒子速度的上限为|vid|≤vmax。

1.2 遗传算法

遗传算法(genetic algorithm，GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐并行性和更好的全局寻优能力；采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则。遗传算法的基本运算过程如下：

(1)初始化：设置进化代数计数器t和最大进化代数T，随机生成初始群体；

(2)个体评价：计算群体各个体的适应度；

(3)选择运算：把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代；

(4)交叉运算：将交叉算子作用于群体；

(5)变异运算：对群体中的个体串的某些基因座上的基因值做变动；

(6)终止条件判断：若t=T，则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

2 PSO_GA数据转换基本原理

电力系统仿真软件间的数据转换就是按照一定的数据转换规则确定目标转换软件中各标准模型的参数值，最终使转换后模型的输出与转换前原有模型的输出基本一致，这一过程可称为数据的等价转换。假设电力系统仿真软件A中有模型S，另一仿真软件B中有模型R，且模型S和模型R表示同一实体。已知S中包含n个属性，模型R中有m个属性(n>m)，且模型S和R中的大部分属性相同，但由于模型本身的微小差异性，有个别属性不同。故此，模型S和R在进行数据转换时其参数不能进行一一对应的直接转换，必须对所设置的初始转换参数进行修正以使模型数据转换的输出一致。通过分析已知模型S、R的数学理论模型，得到S与R之间的转换关系函数F，令a1，a2，…，ak是模型S和R共有的属性，而bk+1，bk+2，…，bn为模型S中的属性，ck+1，ck+2，…，cm为模型R中的属性。则可得：

(3)

为使模型S和R实现无差别的精确转换，可定义

(4)

其中S′为经函数F作用后的转换模型，则模型S和R的数据转换过程可描述为

(1)定义：转换模型S′的输出信号为X，模型R的输出信号为Y。在同一输入信号r的作用下，信号X与信号Y的输出误差为e。若J为数据转换的目标函数，则J是输出误差e的函数。

(2)应用参数辨识理论，调用改进遗传算法不断修正模型R各属性的参数值，直到输出误差e满足目标函数Je最小为止，即满足式(5)的一组模型R各属性的参数值a1，a2，…，ak，ck+1，ck+2，…，cm。转换原理如图1所示。

(5)

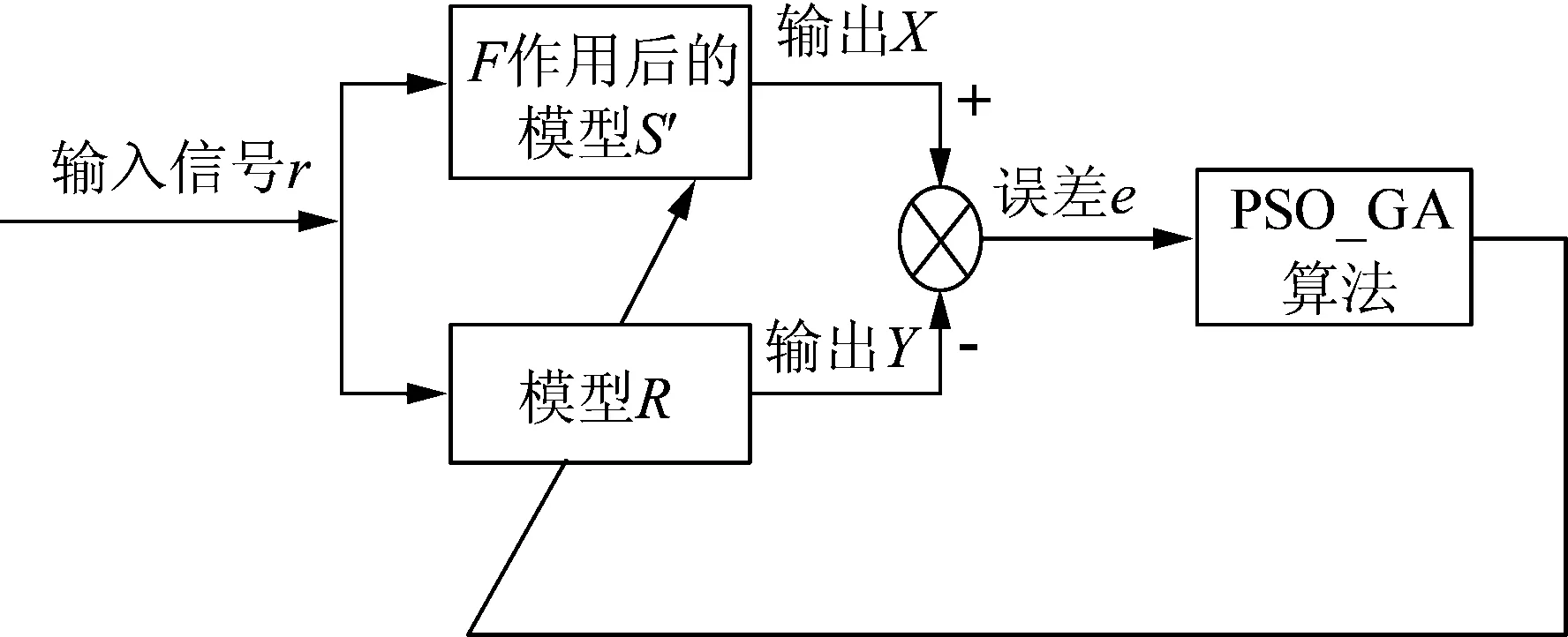
图1 数据转换原理图

3 PSO_GA在数据转换中的应用

3.1 目标函数与约束条件

如图1所示，为使模型S′与模型R在某一相同的输入信号r的作用下输出信号X和Y基本一致，则模型S′、R的中间环节的输出信号也应该基本一致。因此，分别对信号X和Y进行采样，目标函数Je如式(6)所示：

(6)

式中：n是采样点的个数；k为中间输出信号和输出信号的总数；αj是模型R输出信号的调节系数。

为保证复杂网络模型数据转换的准确性，除了要满足上述目标函数，还必须满足以下约束条件。

(1)网络各节点电压的约束：

(7)

(2)网络电流约束：

(8)

(3)发电机电源约束：

(9)

(4)网络潮流约束：

(10)

式中：j为网络中的各节点；J为节点j的集合；Uj、Umax,j、Umin,j分别表示节点j的电压值及其上、下限；Ij、Imax,j、Imin,j表示节点j的电流值及其上、下限；PGmin,j、QGmin,j为发电机电源的有功、无功功率的下限值；PGmax,j、QGmax,j为发电机电源的有功、无功功率的上限值；PG,j、QG,j是发电机的输出功率；PL,j、QL,j是负荷功率。

3.2 PSO_GA算法数据转换

遗传算法通过适应度函数挑选出下一代中的最优解，适应度值大的个体被保留下来；反之，则被淘汰。但在这一过程寻找到的解群可能为局部最优解并非全局最优解。为避免遗传算法易早熟的缺点，提出基于遗传算法、粒子群算法的混合优化 (PSO_GA)。PSO_GA混合优化算法的主要原理是将PSO优化算法引入到GA算法中，用PSO算法构建GA算法中的变异算子，破坏染色体在变异时的随机性而随着以往信息进行有向变异，保证了子代的优良性，使种群快速良性发展。

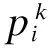
(11)

(12)

式(11)通过权重因子c1、c2和随机数γ1、γ2以及信息反馈、xmax,i、Xmax预测了变异的幅度和方向；式(12)描述了变异操作的具体实施过程。

PSO_GA算法数据转换基本流程如下：

(1)分析对比2种电力系统仿真软件中模型的数据结构差异，依据属性能否直接匹配形成分类的属性列表，调用转换函数F得到转换后模型S′，在PSASP自定义建模平台或Matlab/Simulink建立模型S′和对应模型R，确定数据转换的目标函数式(6)及网络约束式(7)～(10)。

(2)初始群体的生成及参数编码。先将模型R的参数进行分类，然后等分参数的限值区间产生初始群体，最后对参数进行二进制编码。设待修正参数Ari的变化范围是[Amin，Amax]，参数Asi的二进制数为b，则

(13)

将所有待修正参数Ar1，Ar2，…，Arm的二进制编码联结成二进制串p，若有(m-k)个待辨识参数，每个参数的二进制编码均为q位，则二进制串p共有(m-k)q位。

(3)适应度函数f的建立，即个体适应度f为

(14)式中：f(e)如式(9)所示；C、D分别为比例系数和非零的调节参数，用于调节适应度值。由式(14)可知，误差函数f(e)的值越小，适应度f的值越大，该个体被保留的概率越大；反之，则该个体将被淘汰。

(4)确定遗传算子。采用无放回的随机余数选择法和“精英保留”相结合的选择方式：

1)为改变算法的收敛速度，以每次迭代的最优个体和现存的最优个体替换每代中适应度最差的个体；

2)为避免父代中适应度最优的个体在选择、交叉和变异的过程中丢失，在算法执行过程中将父代中的最优个体保存下来直接复制，而不进行交叉和变异操作。

为提高算法的时间效率，提出自适应交叉率，如式(15)所示

(15)

式中Pc1=0.95，Pc2=0.05，fmax为每代群体中的最大适应度值，favg为平均适应度值；f′是待交叉个体中适应度的较大值。

(5)迭代终止判别。PSO_GA算法数据转换流程图如图2所示。

3.3 BPA到PSASP的数据转换

3.3.1 模型转换结果

IEEE 43节点算例的SWI文件包含发电机(M、MF)、励磁系统(EA)、PSS稳定器(SS)、调速器(GH)等模型，以电力系统稳定器的数据转换过程为例，验证改进遗传算法对BPA与PSASP软件中励磁模型数据转换的有效性和准确性。

BPA软件中SS稳定器模型与PSASP中1型PSS模型进行转换，图3为SS稳定器模型原理图，图4为1型PSS模型原理图。

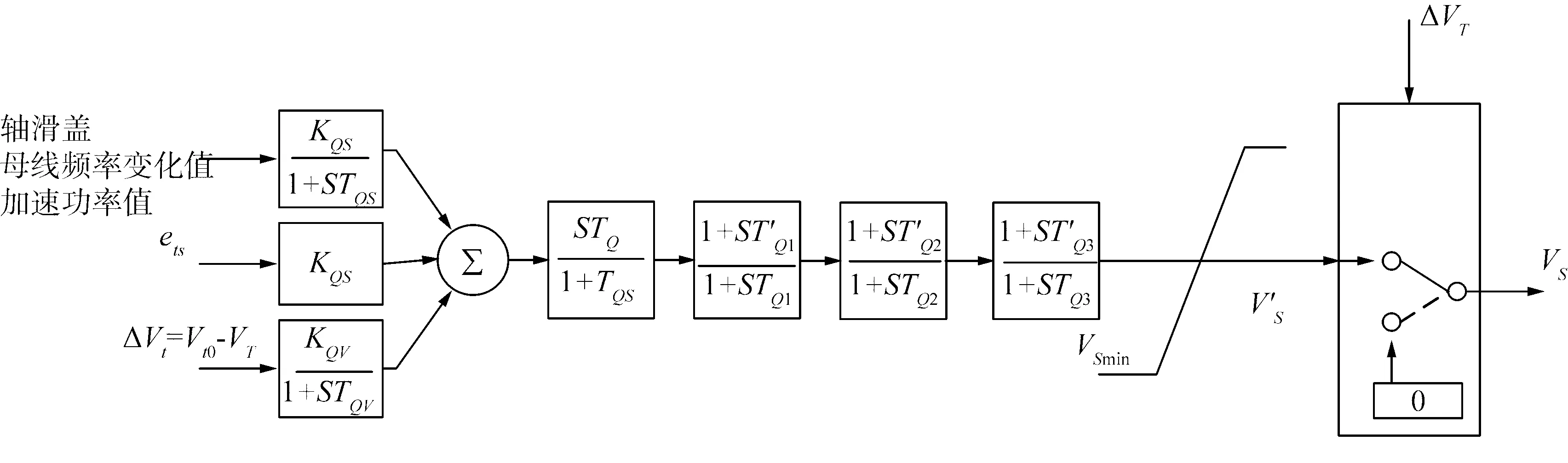
图3 SS模型原理图

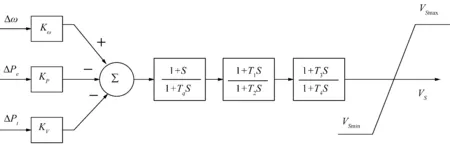
图4 1型PSS模型原理图

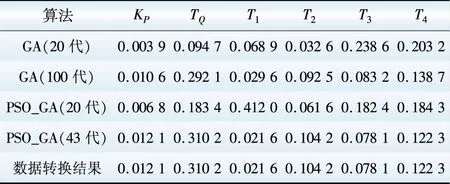
应用PSO_GA算法对1型PSS模型的参数进行修正，使BPA中SS稳定器模型与PSASP软件1型PSS模型在相同的阶跃输入信号作用下，2个模型的输出结果基本一致，基于GA算法与PSO_GA算法数据转换结果对比，如表1所示。

表1 基于GA算法与PSO_GA算法数据转换结果

Table 1 Results of data conversion based on GA and PSO_GA

3.3.2 BPA到PSASP数据转换结果

(1)潮流数据转换结果分析。通过对比BPA和PSASP软件母线电压、相角及全网的潮流仿真数据，其计算结果基本一致，分析2种软件潮流计算结果的差异，发现导致差异的主要原因是仿真软件潮流计算的算法本身的差异性，以及潮流计算中间环节保留的有效位数不同。

(2)暂稳数据转换结果分析。由于潮流计算结果是暂态稳定计算的基础，故在暂稳仿真过程中，为便于分析发电机均采用经典二阶模型，电机转矩阻尼系数设置为2。设置BusB线路开关处发生三相短路故障，经过0.2 s后故障线路跳开。图5、6分别为暂态稳定母线1电压曲线、励磁电压波形。

从图5、6中可看出采用PSO_GA算法BPA到PSASP暂稳数据转换的结果基本一致。

4 结 语

通过研究PSO_GA混合优化算法的基本理论，提出基于PSO_GA算法BPA向PSASP数据转换，通过IEEE 43节点的系统算例对BPA向PSASP数据转换过程进行了验证，验证了该方法对BPA向PSASP数据转换的有效性，提高了数据转换的准确度和算法的运行速度，为电力系统仿真软件异构数据源间的数据共享提供了参考和借鉴。

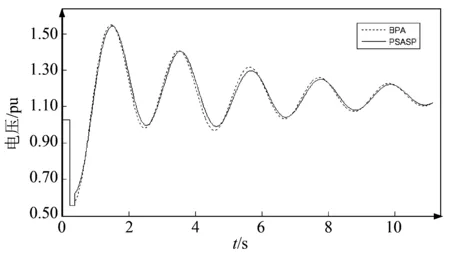
图5 暂态稳定母线1电压曲线

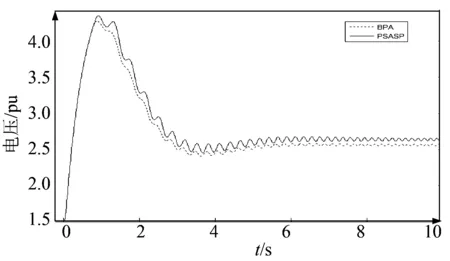
图6 励磁电压曲线

[1]张民，贺仁睦，许津津，等.图论在BPA模型向PSCAD模型自动转换中的应用[J].电网技术，2012，36(6)：163-169. Zhang Min, He Renmu, Xu Jinjin, et al. Application of graph theory in approach for automatically converting BPA models into PSCAD/EMTDC models[J].Power System Technology,2012，36(6):163-169.

[2]张松涛，宁庆，曹国云.BPA向PSS/E的数据转换及暂态稳定比较研究[J]. 电力系统及其自动化，2013，35(4)：63-64. Zhang Songtao, Ning Qing, Cao Guoyun. Data conversion and transient stability analysis between BPA and PSS/E[J].Electrical Automation,2013,35(4):63-64.

[3]程华，徐政.PSASP与PSS/E 稳定计算的模型与结果比较[J].电网技术，2004，28(5)：1-4，8. Cheng Hua, Xu Zheng. Comparison of mathematical models for transient stability calculation in PSASPAND PSS/E and corresponding calculation results [J].Power System Technology,2004,28(5):1-4,8.

[4]张春晓，张涛.基于最小二乘支持向量机和粒子群算法的两相流含油率软测量方法[J].中国电机工程学报，2010，30(2)：86-91. Zhang Chunxiao, Zhang Tao. Soft measurement method for oil holdup of two phase flow based on least squares support vector machine and particle swarm optimization[J].Proceedings of the CSEE，2010，30(2)：86-91.

[5]符杨，孟令合，罗萍萍，等.基于捕食搜索策略的粒子群算法在输电网络扩展规划中的应用[J].电力建设，2009，30(3)：1-4. Fu Yang, Meng Linghe, Luo Pingping, et al. Application of particle swarm optimization algorithm based on predatory search strategy in transmission power grid expansion planning[J].Electric Power Construction,2009,30(3):1-4.

[6]刘长军.电力系统无功优化控制中遗传算法的改进[J].电力建设，2006，27(12)：18-20. Liu Changjun. Improvements of genetic algorithm in power system optimized reactive power control[J].Electric Power Construction,2006,27(12):18-20.

[7]包广清，杨国金，杨勇，等.基于改进遗传算法的光伏发电并网优化配置[J].电力建设，2014，35(6)：13-17. Bao Guangqing, Yang Guojin, Yang Yong, et al .Optimal allocation of grid-connected photovoltaic generation based on improved genetic algorithm[J]. Electric Power Construction, 2014, 35(6): 13-17.

[8]舒辉，文劲宇，罗春风，等.含有非线性环节的发电机励磁系统参数辨识[J]. 电力系统自动化，2005，29(6)：66-70. Shu Hui, Wen Jinyu, Luo Chunfeng, et al. Nonlinear parameters identification for synchronous generator excitation systems[J].Automation of Electric Power Systems,2005,29(6):66-70.

[9]赵书强，王磊，马燕峰，等.基于改进遗传算法的非线性励磁系统参数辨识[J].电力自动化设备，2007，27(7)：1-4. Zhao Shuqiang,Wang Lei, Ma Yanfeng, et al. Parameter identification of nonlinear excitation system based on improved genetic algorithm[J].Electric Power Automation Equipment,2007,27(7):1-4.

[10]蒋平，王晓伟，王杨正，等.遗传算法的改进策略及其在非线性发电机励磁系统参数辨识中的应用[J]. 电力自动化设备，2008，28(6)：31-35. Jiang Ping, Wang Xiaowei, Wang Yangzheng, et al. Improved strategies of genetic algorithm and their applications in parameter identification of nonlinear generator excitation systems[J].Electric Power Automation Equipment,2008,28(6):31-35.

[11]Yang T, Feng Y X, Ren Y, et al. Parameter Identification of Steam Turbine Speed Governor System [C]// Power and Energy Engineering Conference (APPEEC), 2012 Asia-Pacific，2012.

[12]王晓伟，蒋平，曹亚龙，等.改进遗传算法在发电机励磁系统参数辨识中的应用[J].继电器,2007,35(11):16-20. Wang Xiaowei, Jiang Ping, Cao Yalong, et al. Application of improved genetic algorithm in parameter identification of generator excitation systems[J].Relay,2007,35(11):16-20.

[13]Puma, J Q, Colome D G. Parameters identification of excitation system models using genetic algorithms[C]// 2009 American Control Conference,2009.

[14]Lankarany M, Rezazade A. Parameter Estimation Optimization Based on Genetic Algorithm Applied to DC Motor [C]// Electrical Engineering, 2007. ICEE’07. International Conference，2007.

[15]刘佳，李丹，高立群，等. 多目标无功优化的向量评价自适应粒子群算法[J].中国电机工程学报，2008,28(31)：22-28. Liu Jia, Li Dan, Gao Liqun, et al. Vector evaluated adaptive particle swarm optimization algorithm for multi-objective reactive power optimization[J].Proceedings of the CSEE,2008,28(31):22-28.

[16]程颖，鞠平，吴峰.负荷模型参数辨识的粒子群优化法及其与基因算法比较[J].电力系统自动化，2003,27(11)：25-29. Cheng Ying, Ju Ping, Wu Feng. PS algorithm in load parameter identification and its comparison with genetic algorithm [J].Automation of Electric Power Systems,2003,27(11):25-29.

(编辑:刘文莹)

Data Conversion of BPA to PSASP Based on PSO_GA

YE Qing, ZHU Yongqiang, LI Hongxian

(School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

The data format of existing commercial softwares for power system is not unified, which leads to the existence of a large number of heterogeneous data sources, and difficult data exchange among simulation softwares. To solve this problem, a data conversion method based on particle swarm optimization-genetic algorithm (PSO_GA) was proposed for power system simulation softwares. The differences of component model and control model in simulation software BPA, PSASP were dissected, and then the conversion relationship between corresponding models was established, as well as the objective function and associated constraints of intelligent optimization algorithm (PSO_GA). The parameters of each model in objective conversion software were corrected based on PSO_GA to achieve the data conversion of power system simulation software BPA to PSASP. By the example of IEEE 43 system, the data conversion process of BPA to PSASP was validated, the effectiveness of the method for the data conversion of power system simulation software was demonstrated, and the accuracy of data conversion and the speed of the algorithm were improved.

genetic algorithm; particle swarm optimization (PSO) algorithm; BPA; PSASP; model transformation; data conversion

S′=F(a1,a2,…,ak,bk+1,bk+2,…,bn)

minJe=minf(e)

Umin,j≤Uj≤Umax,j

Imin,j≤Ij≤Imax,j

f=C/[D+f(e)]

TM 74

A

1000-7229(2015)04-0104-06

10.3969/j.issn.1000-7229.2015.04.017

2014-10-19

2014-12-08

叶青(1990)，女，硕士研究生，主要研究方向为新能源电力系统；

朱永强(1975)，男，博士，副教授，主要研究方向为新能源发电与并网技术；

李红贤(1992)，女，硕士研究生，主要研究方向为新能源发电。