基于系统有功网损-风速灵敏度的双馈机风电场并网位置研究

李生虎，张维，汪秀龙

(合肥工业大学电气与自动化工程学院，合肥市 230009)



基于系统有功网损-风速灵敏度的双馈机风电场并网位置研究

李生虎，张维，汪秀龙

(合肥工业大学电气与自动化工程学院，合肥市 230009)

关于风电并网对网损影响的分析，有助于风电系统安全经济运行，但是现有网损灵敏度指标，不能直接反映风速波动影响。在最大功率点跟踪(maximum power point tracking，MPPT)方式下，考虑双馈感应发电机(doubly-fed induction generator，DFIG)内部损耗时，有功出力与定子电压有关，在潮流求解前未知。基于并网DFIG潮流模型，拓展网损灵敏度算法，提出电网有功网损对风速的灵敏度模型，以反映有功网损受风速影响及趋势。量化DFIG不同无功控制方式对网损及风速灵敏度的影响。考虑风速概率区间分布，综合分析灵敏度结果对风电场选址和双馈感应风电机组无功控制方式的辅助参考价值。算例结果证明了所提灵敏度模型的可行性和正确性。

有功网损；灵敏度；风速；双馈感应电机(DFIG)；无功控制；并网点

0 引 言

由于风电并网具有随机性、间歇性和不可控性，因此会影响电网安全经济运行。文献[1]认为恒速风电机组并网制约因素主要是电压越限。文献[2]认为并网后电压波动和闪变原因是风电功率波动。文献[3]计算风电系统电压稳定性裕度概率分布，以期发现潜在危险及薄弱环节。上述研究基于恒速机组，并网后需从电网吸收无功，造成电压波动，因此逐步被双馈和直驱型等变速机组取代。由于结构和特性差异，对恒速机组的结论未必适合变速机组。文献[4-5]采用概率统计和时间序列法分析风电并网后功率波动情况。文献[6-7]基于风电基地实测数据，分析大规模风电并网对系统安全稳定的影响。上述文献研究结论具有工程参考价值，但结论依赖于具体系统和实测数据，缺乏理论推导，不便于其他系统应用。

提高风电系统经济性前提之一是量化网损，而上述研究主要集中在电压稳定和无功控制[8-14]。文献[15]基于P-V曲线，给出了不同功率因数下，风电出力对网损的影响，但是基于仿真结果，缺乏理论推导，不便于进一步推广。双馈感应发电机(doubly-fed induction generator，DFIG)有功出力受风速变化影响不可控，而无功出力取决于其控制策略(恒电压、恒功率因数或恒无功控制等)。传统网损灵敏度分析，常建立电网有功网损对机组有功出力的灵敏度模型，但双馈风电机组有功出力随风速变化，且机组有功损耗与定子电压(电网潮流)有关，因此不能将现有网损灵敏度算法直接应用于含DFIG风电系统。

为了量化风速对网损的影响，本文拓展了网损灵敏度算法，在最大功率点跟踪(maximum power point tracking，MPPT)方式下，根据DFIG捕捉机械功率、输入风速和有功输出之间的关系，提出系统有功网损对风速的灵敏度模型，判断风速变化时系统有功网损的变化趋势和大小。确定了DFIG不同无功控制方式对灵敏度模型的影响。比较不同接入点和无功控制方式下的有功网损和灵敏度以及风速区间分布，以确定DFIG合适并网位置和无功控制方式。最后给出算例结果以验证该灵敏度模型的可行性和正确性。

1 双馈感应电机潮流模型

1.1 现有分段简化出力模型的不足

现有风电系统稳态分析，常用分段曲线或三次函数近似表示风电机组有功出力P(vw)，前者如下：

(1)

式中：vw为风速；vci、vco、vr分别为切入、切出和额定风速；Pr为额定有功。该模型存在以下误差：

(1)没有考虑不同机组捕捉风能差异，也没有遵循风能利用系数Cp与转速、风速间的关系。如图1所示，在MPPT方式下，分段出力线性模型结果出力偏大。

(2)风力机捕捉风能不等于风电机组出力，二者间相差机械损耗、电机定转子铜损、变流器损耗。在稳态分析时，应该可以计算出铜损。

因此有必要引入风电机组内部约束，与电网联立求解，尽可能精确量化不同风速下风机机组有功出力，以提高模型精确性、减小误差。

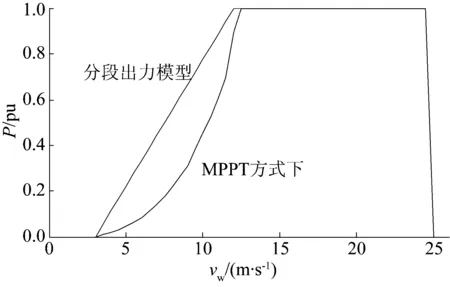
图1 DFIG分段出力模型误差

1.2 风力机出力和转速标幺值

N台并联DFIG的机械功率Pwt*(标幺值)如下：

(2)

式中：SB为电网基准功率；ρ为空气密度；D为叶片直径，指数表达形式如下：

(3)

式中：c1到c9为系数项；λi为中间变量；β为桨距角；叶尖速比为λ，定义如下：

(4)

式中ωwt为风力机转速。

当风速vw低于额定值时，DFIG按MPPT方式运行，ωwt随风速变化而调节，确保Cp为其最大值Cp,max。此时对应的转速为机组最优转速ωwt,opt，转差率s为最优转差率sopt：

(5)

式中：p为极对数；η为齿轮箱增速比；f为电网频率。

1.3 MPPT方式下DFIG内部约束

DFIG结构和等值电路如图2～3所示[16]，其中U,I,R,X,Z分别表示电压、电流、电阻、电抗和阻抗；下标s, m, r, g, T分别表示定子节点、定转子间虚拟节点、转子、网侧变流器和变压器。

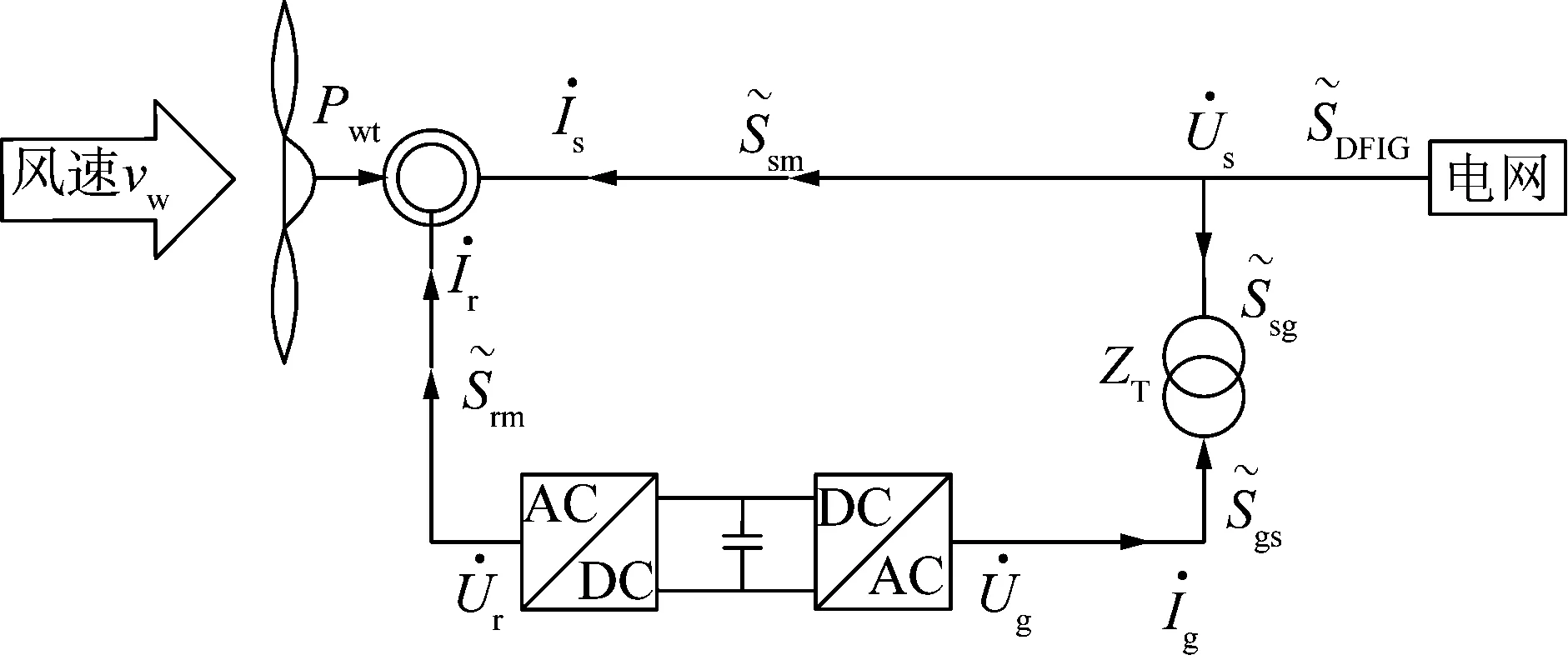
图2 双馈感应电机结构

图3 双馈感应电机等值电路

从电网看向DFIG，定子节点有功、无功功率平衡关系ΔPs,sys、ΔQs,sys如下：

(6)

(7)

式中：PDFIG,set、QDFIG,set为有功、无功出力设定值；PDFIG、QDFIG为实际有功、无功出力。

从DFIG内部看时，对于定子节点，其有功、无功功率平衡关系ΔPs、ΔQs如下：

(8)

(9)

式中：Psm、Qsm分别为定子节点到定转子间虚拟节点的有功、无功功率；Psg、Qsg分别为定子节点到网侧变流器的有功、无功功率。

对定转子间对应激磁支路的虚拟节点，有功、无功功率平衡关系ΔPm、ΔQm如下：

(10)

(11)

式中：Pms、Qms分别为定转子间虚拟节点到定子节点的有功、无功功率；Pmr、Qmr分别为定转子间虚拟节点到转子的有功、无功功率；Qmm为定转子间虚拟节点的无功功率。

对于变流器，其有功、无功功率平衡关系ΔPg、ΔQg如下：

(12)

(13)

式中：Prm为转子到定转子间虚拟节点的有功功率；Pgs、Qgs分别为网侧变流器到定子节点的有功、无功功率；Qg,set为网侧变流器无功出力设定值。

转矩平衡方程ΔT为

(14)

式中Pem为电磁功率。

1.4 MPPT方式下含DFIG的潮流方程

传统潮流计算的修正方程如下：

(15)

式中：ΔPsys、ΔQsys为节点有功、无功功率不平衡量；H、N、J、L为雅可比矩阵元素；Δθsys、ΔUsys为系统电压相角和幅值的修正量。将式(6)～(14)的平衡方程作为其潮流计算的约束条件，得到双馈风电机组并网后的修正方程：

(16)

式中：Jsys、Jsys,DFIG、JDFIG,sys、JDFIG为扩展后的相应雅可比矩阵元素；Δθm、ΔUm、Δθr、ΔUr、Δθg、ΔUg分别对应定转子间虚拟节点、转子和网侧变流器的电压相角和幅值的修正量。当风速变化时，根据式(3)，即可搜索得到风力机出力最大值，代入潮流计算。进一步考虑DFIG不同无功控制方式对潮流结果影响。

(1)在恒无功方式下，无功出力设定值QDFIG,set已知，有功出力PDFIG,set未知，因此联立式(6)和式(8)，得到定子节点的有功约束方程：

(17)

(2)在恒功率因数下，双馈机组无功出力随有功出力波动。此时PDFIG,set与QDFIG,set均未知。联立式(7)和式(9)可得定子节点无功约束方程：

(18)

设功率因数为cosφ，则

(19)

联立式(8)、(9)和(19)，得到定子节点无功约束：

(20)

(3)在恒电压方式下，定子电压幅值Us已知，删除定子节点无功约束方程ΔQs,sys、电压修正量ΔUs,sys和相应雅可比矩阵元素即可。

上述算法适用于等值前DFIG或等值后风电场：

(1)若需详细考虑各机组差异和集电系统损耗，或实际工程中需考虑送出线路损耗，可用机组(群)+等值阻抗的模式模拟风电场送出系统和集电系统。其中在单机+等值阻抗模式下，阻抗可模拟送出线路(风电场整体采用恒电压、恒功率因数或恒无功控制模式)；多机+等值阻抗模式下，可模拟场内集电系统+送出线路(风电机组采用不同无功控制模式)。此时只需在对应新增线路和节点，修改输入原始数据，无需修改算法或程序。如图4所示，当风电机组以辐射型结构接入电网时，只需在原系统中增加a1、a2、a3、a4、b1、b2、b3、b4、c和d节点，以及节点间线路或变压器即可。

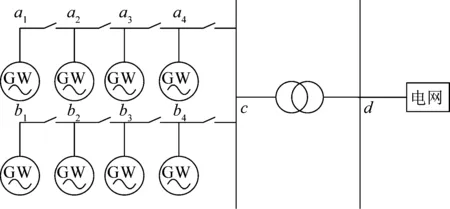
图4 风电场辐射型结构

(2)风电机组和风电场无功控制方式未必相同，式(17)～(20)处理了前者。若需考虑风电场无功控制，需计及公共连接点(PCC)及风场内无功补偿装置，区分可控和固定并补，将其视为PV或带静态电压特性的PQ节点，同样只需改变原始数据，无需修改算法和程序。

2 DFIG在MPPT方式下有功网损对风速灵敏度模型

2.1 系统有功网损对有功出力灵敏度

网损Ploss等于所有节点注入功率之和[17]：

(21)

式中：Ui、Uj分别为节点i、j的电压幅值；Gij为节点间互电导；θij为节点电压相角之差。

式(21)分别对除平衡节点外任意节点k的θk和Uk求导，得：

(22)

(23)

由式(22)和(23)可得：

(24)

式中行向量各元素即为系统有功损耗对各节点电压相角和幅值的灵敏度。

（1）速度提升。根据胜利石油管理局提速提效考核细则的总体要求以及各个区块的考核指标，各个区块基本上达到了10%的提速目标，大北、桩23等区块提速效果超过30%。

结合潮流修正方程式(16)，可得系统有功网损对各节点注入功率的灵敏度：

(25)

式中J为雅可比矩阵，由此可得到系统有功网损对风电机组有功出力灵敏度，但是从1.4节可以看出，双馈机组损耗和有功出力在潮流求解前未知，因此该式不能准确反映风速变化对网损影响。

2.2 系统有功网损对风速灵敏度

将潮流修正方程式(16)简记如下：

(26)

可见网损变化量与节点电压变化量有关，因此若建立了电压变化量与风速变化量的关系，可得到有功网损对风速的灵敏度。扩展潮流修正方程[18]：

(27)

式中：Jv为扩展的列向量，元素为Δf中各不平衡量对风速vw求偏导，除了∂ΔT/∂vw，其余偏导数均为0。由式(2)～(5)和(14)可得：

(28)

潮流收敛时，Δf=0，将式(27)展开得式(29)，从而建立电压幅值和相角与风速灵敏度(式(30))。

(29)

(30)

联立式(24)和(30)，本文提出有功网损对于风速的线性关系如下，其中ξ即为二者之间的灵敏度。

(31)

风电场选址基本条件包括风能资源、地理位置、投资费用，以及电压偏移、功角稳定等。网损是电网稳态经济运行的关键指标之一。电网调度根据上网报价和网损决定各机组出力分配方案。若风电并网导致网损大幅增加，可能被削减出力。因此其他条件相近时，网损对风速灵敏度可作为风场选址、风电机组控制模式的辅助决策依据。

(1)网损灵敏度随风速变化而变化。考虑削减出力可能性，可以采用风速较大时的网损灵敏度。

(2)若需考虑负荷变化，可采用时序负荷数据或区分大、中、小方式代入计算。考虑削减出力可能性，可以采用负荷较小时的网损灵敏度。

3 算例分析

3.1 原始数据

为便于检验灵敏度模型效果，测试系统取一较小的5节点系统(图5)，其中5号节点为平衡节点，电压幅值为0.98，其余均为PQ节点。对于大电网，风场附近线路损耗灵敏度较大，算法相同。

图5 测试系统结构

双馈电机参数如下。风力机参数：c1=0.73，c2= 151，c3=0.58，c4=0.002，c5=2.14，c6=13.2，c7=18.4，c8=-0.02，c9=-0.003；D=71 m；转速范围6～21.5 r/min；增速比η=94；空气密度ρ=1.225 kg/m3。电机参数：UN=690V；PN=2 MW；p=2，Rs=0.007 8 pu；Xs=0.079 4 pu；Rr=0.025 pu；Xr=0.4 pu；Xm=0.0078 pu；RT=0.03 pu；XT=0.05 pu。将同型DFIG并联等效为1台双馈风电机接入系统。若需细分风电机组，则将具体馈线输入原始数据即可。

3.2 等效后风电场接入位置和无功控制方式

考虑不同并网位置和无功控制方式，计算系统有功网损和灵敏度，风速范围取6～10.5 m/s。限于篇幅，给出恒无功出力方式下结果，如表1所示。

表1 双馈机组恒无功出力方式下系统有功网损和灵敏度

Table 1 Active power loss and sensitivity with DFIGs at constant var output mode

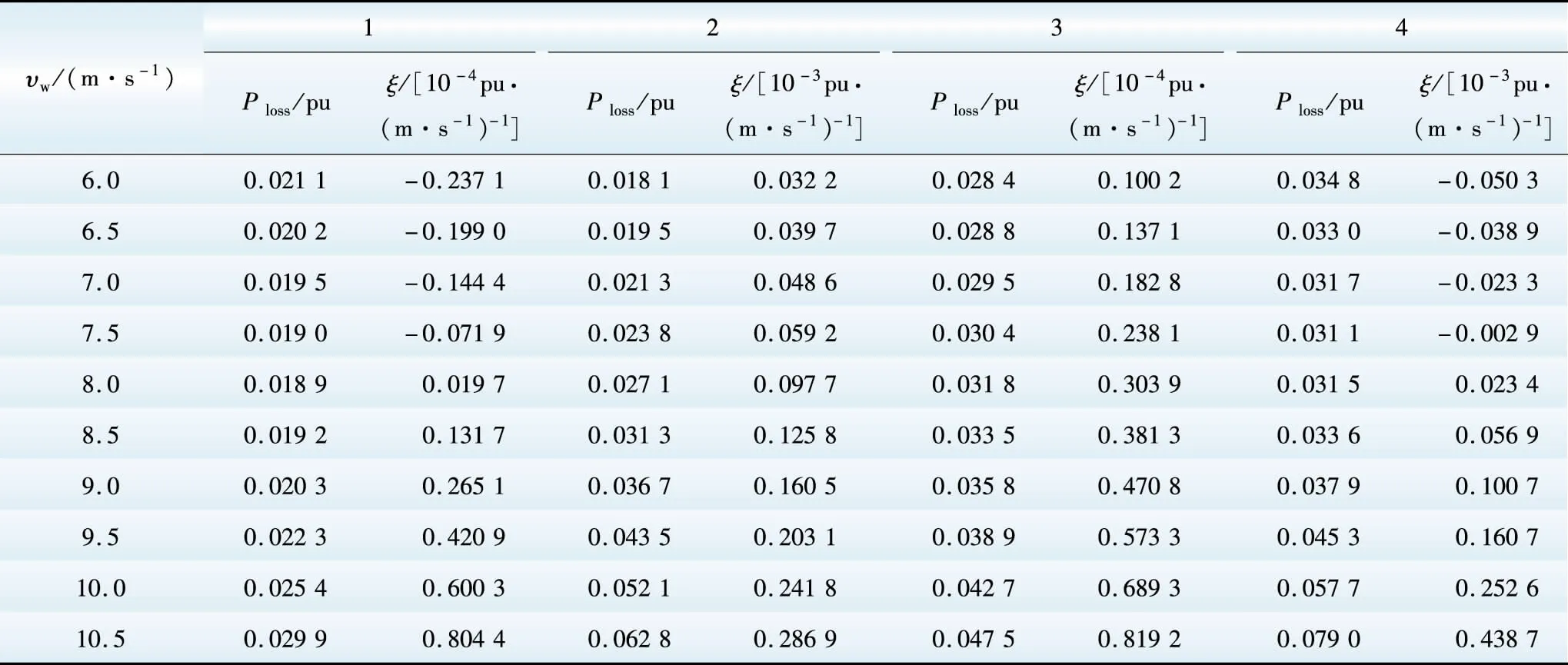
根据计算结果，绘制3种无功控制方式下，不同并网节点对应的有功网损Ploss和灵敏度指标ξ变化曲线，如图6、7所示。

首先分析并网位置对网损影响。从图6可见，当接入节点1或节点4，有功网损和灵敏度的变化情况相似。当风速较小时，灵敏度ξ为负值，此时随着风速增大，有功网损逐渐减小；当风速较大时，灵敏度ξ为正，有功网损随着风速增大而逐步回升。接入节点1时有功网损较接入节点4时低，并且在较大风速下，后者对应灵敏度ξ明显大于前者。因此随着风速变化，接入节点4时对应的有功网损变化明显，而接入节点1时网损受风速变化影响不大。由图7可知：接入节点2或3时，由于对应灵敏度ξ均为正值，有功网损随着风速的增加而不断增大。在低风速下，接入节点2时有功网损较接入节点3时小，随着风速的增加，前者网损逐渐超过后者，其原因是前者灵敏度ξ大于后者，在较高风速时差异更加明显，因此，接入节点2与接入节点3相比，前者系统有功网损更容易受到风速变化的影响。

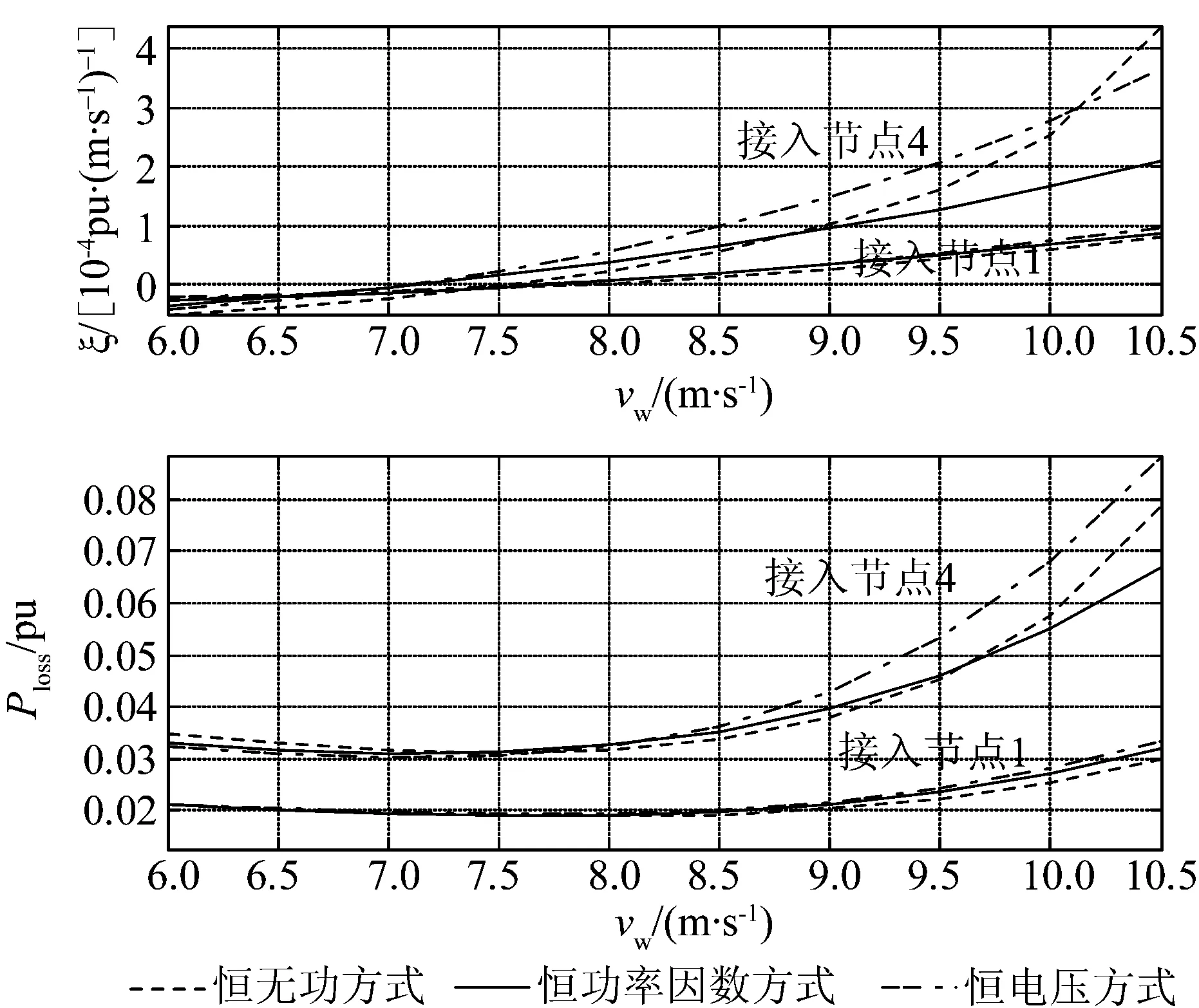
图6 风电场接入节点1和4时有功网损和灵敏度

图7 风电场接入节点2和3时有功网损和灵敏度

其次分析3种无功控制方式对网损影响。由图6、7可见，当双馈机组接入不同节点时，不同无功控制方式所对应的系统网损和灵敏度ξ大小和变化趋势不同。当接入节点1或3时差异较小，其中恒电压方式下对应的灵敏度ξ最大，因此系统有功网损受风速影响最大；恒无功方式下系统有功网损受风速影响最小；接入节点2或4时，在较低风速时，3种控制方式下差异不明显；在较高风速时恒电压方式下的灵敏度ξ最大，其次是恒无功方式，在恒功率因数方式下对应的灵敏度ξ最小，因此对于接入2、4节点情况，双馈机组在恒电压方式下的系统有功网损受风速变化影响最大，而恒功率因数方式下受风速影响最小。

综上所述，接入节点2或节点3时灵敏度ξ为正值，系统有功网损会随着风速的增加而不断增大，不利于提高系统的经济效益和输电效率，但相比之下，接入节点3的灵敏度较小，网损增加不明显，且低风速段时系统有功网损较小。故若在节点2和节点3之间做选择，接入节点3更好；在低风速段接入节点1或4时，灵敏度为负值或接近于0，有功网损受风速变化影响小，可以作为合适的接入点。其中当接入节点4时，由于恒功率因数控制方式下，灵敏度ξ较其余2种方式下小，网损受风速影响相对较小，故宜采用恒功率因数控制方式，以保证系统的网损不会偏高。

因此本算例中最合适接入点为节点1，其次是节点3和4。其中接入节点4时宜采用恒功率因数控制方式。

3.3 某风电场在不同风速段合理接入位置

从统计学来说，按小时均值的风速，一般服从Weibull分布。其分布函数如下：

(31)

式中：k为形状参数；c是标度参数。

取k=4.85，c=2，μ=0。将风速 3～11 m/s(额定风速以下)分为4个风速区间，计算处于不同风速段的概率。分别将风电场接入系统的节点1、节点2、节点3和节点4，计算不同风速段对应的系统平均有功网损Ploss,a和平均有功网损对风速灵敏度ξa。由于篇幅限制，仅给出该风电场在恒无功控制方式下对应的结果，见表2。

表2 不同风速下平均网损和平均灵敏度

Table 2 Average transmission loss and sensitivity with different wind speeds

对风速区间1和2，接入节点1和4平均灵敏度为负，即随着风速增加，网损呈减小趋势，有利于提高输电效率。接入节点3时，虽然平均灵敏度为正，但其值较小，网损受风速影响小，且平均网损也较小。因此对于这2个风速区间，风电场接入节点1最合适，其次是节点3和节点4。

对风速区间3，接入节点1、2、3、4的平均灵敏度均为正值，即随着风速增加，系统有功网损呈现增加趋势。其中接入节点2时系统平均有功网损虽然最小，但平均灵敏度最大，因此系统有功网损受风速影响较大，不宜作为接入点；同样接入节点4时平均灵敏度也较大。因此对于此风速区间，接入节点1和节点3较合适。

对风速区间4，接入各节点的平均灵敏度均为正，其中接入节点1时平均灵敏度最小，且对应的有功网损均值也最小，故接入节点1较合适。

由分布概率知风速大都处于3～7 m/s，即区间1和2内，因此结合区间1和2对应的最佳接入点，可得到该风电场接入节点1最合适，其次是节点3和节点4。

4 结 论

本文在双馈风电机组并网潮流模型的基础上，根据输入风速、捕捉功率和有功出力的关系，提出系统有功网损对风速的灵敏度，得到以下结论：

(1)有功网损对风速灵敏度，可作为风电场选址的辅助参考依据。风电场选址以靠近电网接入点为原则，以减少输电损耗。风电并网后网损增量越少、风场出线损耗越小，经济性越好。根据灵敏度模型，风电场尽量选择并网后灵敏度为负值或绝对值较小的接入点，前者可使系统网损随着风速的增大而减小，以提高系统输电效率；后者可平抑风速波动对系统有功网损的影响。

(2)网损对风速灵敏度指标，可作为确定风电机组无功控制方式的辅助参考依据。当接入点确定时，双馈感应电机恒无功方式、恒功率因数方式和恒电压方式下，灵敏度指标大小和变化趋势不同。为了减小风速波动对系统有功网损的影响，尽量选择灵敏度较小时对应的无功控制方式。

本文提出的网损对风速灵敏度，可作为风场选址和选择风电机组无功控制方式的辅助判据。如何将其与现有基本判据(风能资源、地理位置、投资费用等)结合起来得到更有工程应用价值的风场设计方案将是下一步研究的问题。

[1]吴俊玲，周双喜，孙建锋，等.并网风力发电场的最大注入功率分析[J].电网技术，2004，28(20)：28-32. Wu Junling，Zhou Shuangxi，Sun Jianfeng，et al.Analysis on maximum power injection of wind farm connected to power system[J].Power System Technology，2004，28(20)：28-32.

[2]李渝，范高锋，李庆，等.达坂城风电接入系统对新疆电网电能质量的影响[J].电网技术，2007，31(6)：88-92. Li Yu，Fan Gaofeng，Li Qing，et al.The impact of Dabancheng wind farm integration on power quality of Xinjiang power grid[J].Power System Technology，2007，31(6)：88-92.

[3]王海超，戴剑锋，周双喜，等.含风电场电力系统电压稳定裕度模型[J].清华大学学报：自然科学版，2006，46(7)：1185-1188. Wang Haichao，Dai Jianfeng，Zhou Shuangxi，et al.Voltage stability margin model for power systems containing wind energy resources[J].Journal of Tsinghua University：Science & Technology，2006，46(7)：1185-1188.

[4]侯佑华，房大中，齐军，等.大规模风电入网的有功功率波动特性分析及发电计划仿真[J].电网技术，2010，34(5)：60-66. Hou Youhua，Fang Dazhong，Qi Jun，et al.Analysis on active power fluctuation characteristics of large-scale grid-connected wind farm and generation scheduling simulation under different capacity power injected from wind farm into power grid[J].Power System Technology，2010，34(5)：60-66.

[5]Doherty R，Denny E，O’Malley M.System operation with a significant wind power penetration[C]//IEEE Power Society General Meeting，Denver，America，2004.

[6]汪宁渤，马彦宏，王建东.大规模风电集中并网对电力系统安全稳定的影响[J].电力建设，2011，32(11)：77-80. Wang Ningbo，Ma Yanhong，Wang Jiandong.Analysis of power system security and stability caused by large-scale wind power grid integration[J].Electric Power Construction，2011，32(11)：77-80.

[7]路亮，汪宁渤，马彦宏，等.酒泉风电基地大规模风电并网综合解决方案初探[J].电力建设，2013，34(1)：7-11. Lu Liang，Wang Ningbo，Ma Yanhong，et al.Comprehensive solution for Jiuquan large-scale wind power integration[J].Electric Power Construction，2013，34(1)：7-11.

[8]迟永宁，王伟胜，戴慧珠.改善基于双馈感应发电机的并网风电场暂态电压稳定性研究[J].中国电机工程学报，2007，27(25)：25-31. Chi Yongning，Wang Weisheng，Dai Huizhu.Study on transient voltage stability enhancement of grid-connected wind farm with doubly fed induction generator installations[J].Proceedings of the CSEE，2007，27(25)：25-31.

[9]杨桦，梁海峰，李庚银.含双馈感应电机的风电场电压协调控制策略[J].电网技术，2011，35(2)：121-126. Yang Hua，Liang Haifeng，Li Gengyin.A coordinated voltage control strategy for wind farm containing doubly fed induction generators[J].Power System Technology，2011，35(2)：121-126.

[10]Aghatehrani R，Fan L，Kavasseri R.Coordinated reactive power control of DFIG rotor and grid sides converters [C]//Power & Energy Society General Meeting，Alberta，Canada，2009.

[11]刘勇.电网短路故障对并网双馈风电场的影响[J].电力建设，2012，33(9)：94-97. Liu Yong.Impact of short circuit fault on grid connected operation of doubly fed induction generator wind farm[J].Electric Power Construction，2012，33(9)：94-97.

[12]刘广东，高宁，王东，等.电网不对称故障下双馈式风电机组低电压穿越技术[J].电力建设，2011，32(12)：79-83. Liu Guangdong，Gao Ning，Wang Dong，et al.Low voltage ride through technology of double-fed wind turbine unit under asymmetrical grid[J].Electric Power Construction，2011，32(12)：79-83.

[13]李强,李凤婷,樊艳芳,等.风电并网对接入地区电压的影响[J].中国电力,2012,45(4):15-18. LI Qiang , LI Feng-ting , FAN Yan-fang , et al.Voltage influence of wind power integration[J].Electric Power,2012,45(4):15-18.

[14]刘开俊.风电并网对电网的影响分析及解决方案[J].中国电力,2012,45(9):7-10,16. LIU Kai-jun.Impacts and Solutions of Wind Power Integration on Grids[J].Electric Power,2012,45(9):7-10,16

[15]张义斌，王伟胜，戴慧珠.基于P-V曲线的风电场接入系统稳态分析[J].电网技术，2004，28(23)：61-65. Zhang Yibin，Wang Weisheng，Dai Huizhu.P-V curve based static analysis for integration of wind farm into power system[J].Power System Technology，2004，28 (23)：61-65.

[16]Li S.Power flow modeling to doubly-fed induction generators (DFIGs) under power regulation[J].IEEE Transactions on Power Systems，2013，28(3)：1-10.

[17]石磊，陈恳，张伯明，等.雅可比矩阵法计算有功网损微增率公式的推导[J].南昌大学学报，2001，23(2)：55-58. Shi Lei，Chen Ken，Zhang Boming，et al.Derivation of formulas calculating active incremental transmission losses with Jacobian matrix method[J].Journal of Nanchang University，2001，23(2)：55-58.

[18]Li S.Power flow control effect with TCSC on operation margin of zone 3 impedance relays[J].International Journal of Electrical Power & Energy Systems，2010，32(9)：998-1004.

(编辑:张媛媛)

Integration Point of Doubly-Fed Induction Generator Wind Farm Based on Active Power Loss and Wind Speed Sensitivity

LI Shenghu, ZHANG Wei, WANG Xiulong

(School of Electrical Engineering and its Automation, Hefei University of Technology, Hefei 23009, China)

Research on the impact of wind power integration on transmission loss is beneficial to the safe and economic operation of wind power system. However, the existing sensitivity index of transmission loss cannot directly reflect the influence of wind speed fluctuation. Under the maximum power point tracking (MPPT) strategy, active power output of doubly-fed induction generator (DFIG) is dependent on the stator voltage, and unknown before power flow solution due to its power loss. Based on power flow model of DFIGs, transmission loss sensitivity model was extended to propose new model for the sensitivity of active power loss to wind speed, which could reflect the influence of wind speed on active power loss and its tendency. The influence of var control modes for DFIGs on transmission loss and wind speed sensitivity was quantified. With considering wind speed probability interval distribution, the auxiliary criterions of sensitivity results on the location of wind farm and the var control modes of DFIGs were compositely analyzed. The results validate the feasibility and accuracy of the proposed sensitivity model.

active power loss; sensitivity; wind speed; doubly-fed induction generator (DFIG); var control; integration point

ΔPs,sys=PDFIG,set-PDFIG=0

ΔQs,sys=QDFIG,set-QDFIG=0

ΔPs=-PDFIG,set-Psm-Psg=0

ΔQs=-QDFIG,set-Qsm-Qsg=0

ΔPm=-Pms-Pmr=0

ΔQm=-Qms-Qmm-Qmr=0

ΔPg=-Prm-Pgs=0

ΔQg=Qg,set-Qgs=0

ΔPs,sys=-Psm-Psg-PDFIG=0

ΔQs,sys=-Qsm-Qsg-QDFIG=0

QDFIG,set=PDFIG,settanφ

ΔQs=-Qsm-Qsg-(-Psm-Psg)tanφ=0

Δf=-JΔx

JΔx+JvΔvw=0

Δx=-J-1JvΔvw

国家自然科学基金项目(51277049)。

TM 614

A

1000-7229(2015)04-0008-08

10.3969/j.issn.1000-7229.2015.04.002

2014-11-12

2015-01-30

李生虎(1974)，男，博士，教授，博士生导师，研究领域为电力系统规划与可靠性、风电系统分析与控制、柔性输电技术在电力系统中应用；

张维(1991)，男，硕士研究生，研究方向为风电系统潮流控制和概率仿真；

汪秀龙(1993)，男，硕士研究生，研究方向为直流输电系统运行与控制。

Project Supported by National Nature Science Foundation of China(51277049).