数字图像相关方法测量芳纶纤维复合材料I型裂纹应力强度因子

郝文峰， 陈新文， 邓立伟， 王 翔， 姚学锋

(1.北京航空材料研究院航空材料检测与评价北京市重点实验室，北京100095;2.清华大学工程力学系，北京100084)

数字图像相关方法(digital image correlation，DIC)是一种非条纹光测方法，它是现代先进的光电子技术、数字图像处理技术与计算机技术相结合的产物，它直接对物体变形前、后的两幅散斑图像进行相关运算处理，以提取散斑图中所携带的变形信息。散斑是变形信息的载体，可以通过人工制斑获得或者就直接以试件表面的自然纹理作为标记。

在二维数字图像相关方法的应用方面，国内外都开展了大量的工作。Corr等［1］利用数字图像相关方法研究了纤维复合材料与混凝土界面的粘接强度，得到较为精确的表面变形场。Fedele等［2］利用数字图像相关方法研究GLARE层板层间粘接层材料参数，将材料参数用于有限元模拟，并将模拟结果与试验进行对比。Rjafiallah等［3］提出一种三相模型来分析玻璃微珠增强聚合物基复合材料界面相影响，并用数字图像相关方法进行试验验证。Desai等［4］利用数字图像相关方法测得的位移场计算得到双材料界面裂纹应力强度因子，并将试验结果与理论和有限元结果进行对比。Carloni等［5］利用数字图像相关方法研究疲劳载荷作用下复合材料-混凝土界面裂纹扩展过程。姚学锋及其合作者对数字图像相关方法开展系统研究［6］，并且将数字图像相关方法成功应用于复合材料压力容器测量［7］、人体颈椎生物力学［8］、有机玻璃黏接力学［9］、圆管残余应力测试［9］和编织复合材料力学性能表征［10～12］等一系列新型材料和新型问题的力学测试。

本工作将数字图像相关方法用于芳纶纤维复合材料I型断裂问题研究，通过最小二乘拟合法提取裂纹尖端应力强度因子，分析数字图像相关方法中的子区域和步长大小对计算结果的影响。

1 基于数字图像相关方法的应力强度因子测量

1.1 二维数字图像相关方法的基本原理

对比变形前、后散斑图像的灰度特征是数字图像相关方法的基本原理。被测试样表面需要有足够多的可识别标志点，一般通过在试样表面喷黑白相间的漆斑作为散斑标志点，并且假设这些散斑点的变形就是试样本身的变形。

进行图像前处理以及选择合理的匹配原则来定义相关度是数字图像相关方法算法的关键。合理的对应关系，通常是基于如下两个前提条件［13］:(1)物体表面上的同一个点在变形前后图像上的灰度保持不变;(2)随机分布的散斑使得图像上的任一个包含有足够多的像素点的子集在灰度分布上具有唯一性。

在二维数字图像相关方法中通常将待计算区域划分为许多小的方形小区域，一般称为相关计算子区域。子区域中像素点的数量决定了子区域的大小，对于一个M×M的方形区域，表示其在横向和纵向各包含M个像素点。相邻两个子区域之间的距离称为步长，步长大小决定了相关计算所得位移场的分辨率。

目前常用的各种二维数字图像相关方法的算法，基本上都是以位移为参数，建立变形前后图像上的像素点间的映射关系，如图1所示，变形前图像上的像素点(x，y)的位移为(u，v)，对应于变形后图像上的点(x'，y')。

图1 数字图像相关方法原理Fig.1 Principle of digital image correlation method

建立映射关系后，再选择一个相关公式，计算变形前后图像子区间的相关系数，当相关系数取极值时，认为子区间的匹配是最佳的，然后可以得到位移等变形量。目前，相关运算方法归纳起来有以下几个主要途径［13］:(1)双参数法;(2)粗细搜索法;(3) Newton-Raphson方法;(4)十字搜索法;(5)爬山搜索法;(6)相关系数梯度法;(7)遗传算法;(8)分形算法。

1.2 最小二乘拟合提取应力强度因子

根据文献［19］，I型裂纹尖端x和y方向位移场可以表示为:

式中，r和θ是裂尖任意点的极坐标，κ为弹性常数，平面应力状态下为，平面应变状态下为3-4ν，ν为泊松比。由于数字图像相关数据由表面位移计算所得，故需考虑平面应力状态。μ为剪切模量。对于靠近裂纹尖端区域式(3)、式(4)第一项起主导作用，而对于远离裂尖区域必须考虑高阶项的影响才能精确得到裂尖位移场。

对于式(3)、式(4)，在二维数字图像相关方法试验中，必须考虑由于刚体位移和平面内转动引起的附加项。因此，对于由数字图像相关方法试验数据提取的位移场公式应修订为:

式中，上标j表示M个数据点中的第j个数据点，其坐标为(xj，yj)。uj和vj为点(xj，yj)在x方向和y方向的位移值。u*，v*分别为x方向和y方向的刚体位移，α为平面内转角。裂尖极坐标和直角坐标的转换关系为

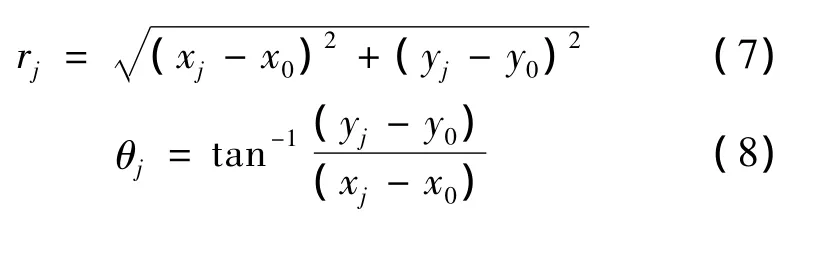
其中(x0，y0)为裂尖处坐标值。由断裂力学获得式(9):

本工作考虑拉伸载荷作用下的正交异性单边裂纹芳纶纤维复合材料板，由最小二乘拟合法来确定式(5)、式(6)中的未知系数。因此，其表达式为［15］:

其中N为式(5)的项数，三个未知数为两个方向刚体位移和转动角。未知参数{χ}，系数矩阵［R］以及向量{Λ}分别为:

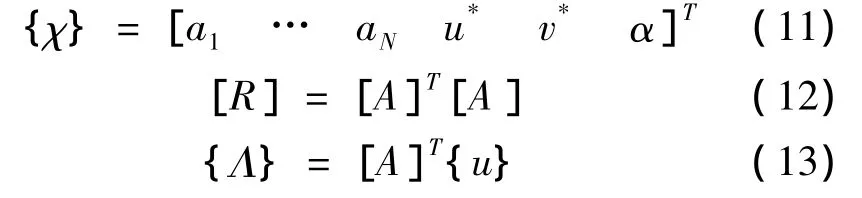
式中［A］为M×N矩阵，包含了u，v表达式中的aN。

本研究拉伸载荷作用下的单边I型裂纹裂尖应力强度因子为:

其中P为拉伸载荷，B为试验件厚度，W为试验件宽度，a为裂纹长度。函数是与试验件尺寸相关的函数，可按文献［21］中的曲线取值，对于本研究试验件几何尺寸=1.25。

2 试验件及试验装置

试验件为3233/023A芳纶纤维复合材料，如图2所示。试验件尺寸如图2a所示，其中试验件宽度W=20mm，长度H=200mm，厚度B=3mm，裂纹长度a=5mm。在试验件正面首先喷上一薄层白漆作为底色，然后再喷上黑漆斑作为数字图像相关的特征斑点，如图2b所示。数字图像相关测试平台及试验装置如图3所示，主要包括试验加载系统、冷光源、CCD相机以及装有数字图像相关算法软件的计算机。试验加载速率为0.5mm/min，试验载荷为0至5000N间隔500N采集一幅图像，CCD相机和冷光源放置于隔震台上以减少试验噪声干扰。试验所用CCD相机分辨率为1280×1024，图像中1mm长度对应于46.5个像素点。为了研究数字图像相关方法中子区域和步长大小对计算结果的影响，本计算中选取五种子区域，其大小分别为21×21，41 ×41，61×61，81×81，101×101，五种步长取子区域长度的0.1至0.5倍，间隔0.1。

图2 试验件 (a)试验件示意图;(b)喷斑后试验件Fig.2 Specimen (a)schematic diagram of specimen; (b)specimens after speckled

图3 试验装置Fig.3 Experimental set-up

3 试验结果及分析

试验件变形前后的散斑场如图4所示，其中图4a为变形前散斑图，图4b为载荷1000N时的散斑图，计算区域以及裂纹位置见图4a，其中黑线位置为裂纹，红色方框内为计算区域。由图4a和图4b无法简单的辨别出差异，但通过数字图像相关方法计算后可以得到试件在x方向和y方向的位移场，如图5a和图5b所示。

图5为数字图像相关方法计算所得全场位移，其中包括刚体位移和面内转动。由图可见，裂纹尖端全场位移分布具有较好的对称性。对图中裂尖部分取半圆按最小二乘拟合方法计算裂纹尖端应力强度因子，对于不同拟合项数和载荷大小计算所得的应力强度因子结果如图6所示。图6a为载荷2000N时不同拟合项次下的应力强度因子值，由图6a可见，在载荷为2000N时，随着最小二乘拟合项数的增加，拟合所得应力强度因子结果与式(14)计算结果的误差越来越小。当只取一项忽略高阶项时，拟合结果与计算结果误差为22.8%，而当取N=5时所得应力强度因子误差减小为4.1%。为减小计算量并保证一定的精度，其他计算均取N=5。图6b为应力强度因子与施加载荷曲线，其中由式(14)计算所得应力强度因子随施加载荷的增加而线性增大。数字图像相关方法计算位移场拟合所得应力强度因子与式(14)计算结果偏差较小。

图4 DIC计算散斑图 (a)变形前散斑图(0N);(b)变形后散斑图(1000N)Fig.4 Speckle field using calculation (a)before deformation(0N);(b)after deformation(1000N)

图5 DIC计算位移场 (a)U场，1000N;(b)V场，1000N;(c)U场，2000N; (d)V场，2000N;(e)U场，5000N;(f)V场，5000NFig.5 Displacement field calculated from DIC (a)U field，1000N;(b)V field，1000N; (c)U field，2000N;(d)V field，2000N;(e)U field，5000N;(f)V field，5000N

图7为载荷2000N时，数字图像相关计算时子区域大小和步长大小对最小二乘拟合所得应力强度因子的影响，由图7a可见子区域大小为41时，拟合结果与式(14)计算结果最为接近，这主要是因为如果区域太小，包含的信息量不够，难以准确匹配二幅散斑图的相关区域;区域太大，则会造成比较严重的平均效果，同样亦难以准确匹配二幅散斑图的相关区域，这两种情况都会降低测量精度。子区域大小为101时误差为6.0%，子区域大小为21时误差为4.7%，均大于子区域大小为41时的4.1%。由图7b可见，子区域大小为41时，数字图像相关计算的步长越小，其结果越接近于式(14)计算结果，五种步长大小计算所得结果偏差均在5%以内。数字图像相关计算时步长大小对结果的影响小于子区域大小的影响。

图6 DIC应力强度因子 (a)拟合项数影响;(b)应力强度因子-载荷曲线Fig.6 Stress intensity factors (a)effect of least squares fitting terms;(b)stress intensity factors-load curve

图7 DIC计算参数影响 (a)子区域大小影响;(b)步长大小影响Fig.7 Effect of DIC parameters (a)effect of subset size;(b)effect of subset spacing

4 结论

(1)通过最小二乘拟合法建立了考虑刚体位移的数字图像相关方法计算所得位移场与I型裂纹尖端应力强度因子之间的关系。

(2)试验研究了含单边I型裂纹芳纶纤维复合材料在拉伸载荷作用下裂纹尖端位移场演化规律。提取裂纹尖端应力强度因子，并将试验结果与理论公式计算结果进行对比，结果表明试验所得应力强度因子与理论结果偏差在10%以内。

(3)分析最小二乘拟合项数、数字图像相关计算子区域大小和步长大小对试验提取应力强度因子的影响，结果表明增加最小二乘拟合项数可以提高应力强度因子测试精度，而数字图像相关计算子区域大小和步长大小的影响较为复杂，需要通过经验或者试算确定合理的区域和步长大小来提高计算精度。

［1］CORR D，ACCARDI M，GRAHAM-BRADY L，et al. Digital image correlation analysis of interfacial debonding properties and fracture behavior in concrete［J］.Engineering Fracture Mechanics，2007，74(1/2):109-121.

［2］FEDELER，RAKA B，HILD F，etal.Identification of adhesive properties in GLARE assemblies using digital image correlation［J］.JMech Phys Solids，2009，57(7):1003 -1016.

［3］RJAFIALLAH S，GUESSASMA S.Three-phasemodel and digital image correlation to assess the interphase effect on the elasticity of carbohydrate polymer-based composites reinforced with glass-silica beads［J］.Carbohyd Polym，2011，83(1):246-256.

［4］DESAIC K，BASU S，PARAMESWARAN V.Determination of complex stress intensity factor for a crack in a bimaterial interface using digital image correlation［J］.Opt Laser Eng，2012，50(10):1423-1430.

［5］CARLONIC，SUBRAMANIAM K V.Investigation of subcritical fatigue crack growth in FRP/concrete cohesive interface using digital image analysis［J］.Composites Part B:Engineering，2013，51:35-43.

［6］MENG L B，JIN G C，YAO X F.Application of iteration and finite element smoothing technique for displacement and strain measurement of digital speckle correlation［J］. Optics and Lasers in Engineering，2007，45(1):57-63.

［7］YAO X F，MENG L B，JIN JC，etal.Full-field deformation measurement of fiber composite pressure vessel using digital speckle correlation method［J］.Polymer Testing，2005，24(2):245-251

［8］MA Y J，XIONG T C，YAO X F.Experimental investigation of interface curing stresses between PMMA［J］.Theoretical＆ Applied Mechanics Letters，2011，1(5): 051003.

［9］MA Y J，YAO X F，ZHANG D W.Axially symmetrical stresses measurement in the cylindrical tube using DIC with hole-drilling［J］.Optics and Lasers in Engineering，2015，66:174-180

［10］MA Y J，YAO X F，ZHENGQ S，etal.Carbon nanotube films change Poisson's ratios from negative to positive［J］. Applied Physics Letters，2010，97(6):061909.

［11］MA Y J，YAO X F，WANG D.Experimental investigation onmechanical properties of CNT film using digital speckle correlation method［J］.Optics and Lasers in Engineering，2012，50(11):1575-1581.

［12］HAOW F，GED Y，MA Y J，etal.Experimental investigation on deformation and strength of carbon/epoxy laminated curved beams［J］.Polymer Testing，2012，31(4): 520-526.

［13］孟利波.数字散斑相关方法的研究和应用［D］.北京:清华大学，2005. (MENG L B.Study and Application of Digital Speckle Correlation Method［D］.Beijing:Tsinghua University，2005.)

［14］YONEYAMA S，MORIMOTO Y，TAKASHIM.Automatic evaluation of mixed-mode stress intensity factors utilizing digital image correla-tion［J］.Strain，2006，42:21-29.

［15］ESHRAGHI I，YADEGARI DEHNAVIM R，SOLTANI N.Effect of subset parameters selection on the estimation ofmode-I stress intensity factor in a cracked PMMA specimen using digital image correlation［J］.Polymer Testing，2014，37:193-200.

［16］CRAVERO S，RUGGIERIC.Estimation procedure of J-resistance curves for SE(T)fracture specimens using unloading compliance［J］.Engineering Fracture Mechanics，2007，74:2735-2757.