两自由度直驱感应电机运动耦合分析

冯星辉，艾立旺，张新良，朱艺锋，司纪凯

(1.河南省电子产品质量监督检验所，郑州450003;2.河南理工大学，焦作454003)

0 引 言

随着工业技术的发展，对多自由度运动驱动技术的需求不断显现。能够做直线、旋转或螺旋运动的两自由度驱动器在机械工具和机器人领域有可观的应用价值［1-3］。这种驱动技术可省去传统驱动装置的机械传动装置，具有结构简单、机械磨损小、可靠性高和维护成本低等优点。由于其结构的特殊性和运动形式的多样性造成对其分析十分复杂，主要原因是其内部的电磁场现象比较复杂且存在运动耦合效应。所以必须研究其内部的电磁场及耦合效应才能准确地分析电机特性。

文献［4］对通过对比解析法、二维和三维计算磁通密度的结果，得出三维分析法的优点:全面考虑三维空间结构的特殊性和多自由度运动的复杂性。并基于三维有限元数值场分析对所提出的旋转-直线开关磁阻电机的复杂结构进行分析。文献［5］提出一种新型旋转-直线各向同性无刷电机结构，在正弦理论前提下进行建模并得出了所述无刷电机的约束方程，又通过三维有限元软件建立基于脚本的三维参数化模型进行仿真计算和特性分析。虽然这些文献采用三维分析方法，但并没有考虑两自由度运动间的相互耦合影响。

文献［6］对于一种两自由度电机——双电枢旋转-直线感应电机的特性进行分析，该电机的直线部分和旋转部分的轴向串联结构决定了其直线部分的纵向端部效应会影响到旋转部分，而旋转部分对直线部分几乎无影响。所以文献［7］所采用动态时域有限元法和频域滑频技术结合的方法对双电枢旋转-直线感应电机的直线部分动态端部效应进行建模分析，即分析了直线运动对旋转运动的影响。文献［8 -9］针对借助于压力机的螺母滑块机构产生直线运动的螺旋运动铁磁体实心转子异步电机，通过运用解析法对实心转子异步电机的电磁场进行计算，分析了转子存在轴向运动时对旋转运动部分参量的影响。

本文针对所提出的两自由度直驱感应电机的特殊结构和运动形式，首先利用Maxwell 方程组建立考虑直线运动和旋转运动之间耦合影响的数学模型进行耦合影响分析，通过有限元软件建立不同运行状态下电机的三维参数化模型，验证分析两自由度直驱感应电机的旋转运动与直线运动之间的耦合影响。

1 基本结构和工作原理

1.1 两自由度直驱感应电机的基本结构

两自由度直驱感应电机主要由旋转运动弧形定子、直线运动弧形定子和动子构成［10-11］。旋转运动弧形定子具有沿轴向的绕组及沿轴向开槽的定子铁心所组成的半圆环形定子。直线运动弧形定子为沿圆周方向开槽的定子铁心与沿圆周的绕组所组成的桥拱形定子，直线运动弧形定子沿内圆周方向按照一定的机械角度开槽。旋转运动弧形定子及直线运动弧形定子经扣合组装成一整体，两个定子铁心在空间上正交分布，两个弧形定子绕组沿圆周分区域正交布置，共用一个复合次级的空心圆柱形动子。定子两部分以及转子配合在一起后的整体结构如图1 所示。

图1 两自由度直驱感应电机结构

1.2 两自由度直驱感应电机的工作原理

所述两自由度直驱感应电机通电后，旋转运动弧形定子会形成旋转磁场，由于电磁感应原理会在动子铁心的表面产生感应电动势并形成电流，最终产生旋转力矩;由直线运动弧形定子会形成做直线运动的行波磁场，由于电磁感应原理在动子铁心的表面会产生感应电动势并形成电流，最终产生轴向方向的力。该电机采用两套定子绕组，当只有直线运动弧形定子绕组通电时，可以驱动负载做轴向直线运动;当只有旋转运动弧形定子绕组通电时，可以驱动负载做旋转运动;当两者同时通电时，旋转力矩和轴向的力共同作用在电机动子上，实现电机动子的螺旋运动［12-13］。电机主要参数如表1 所示。

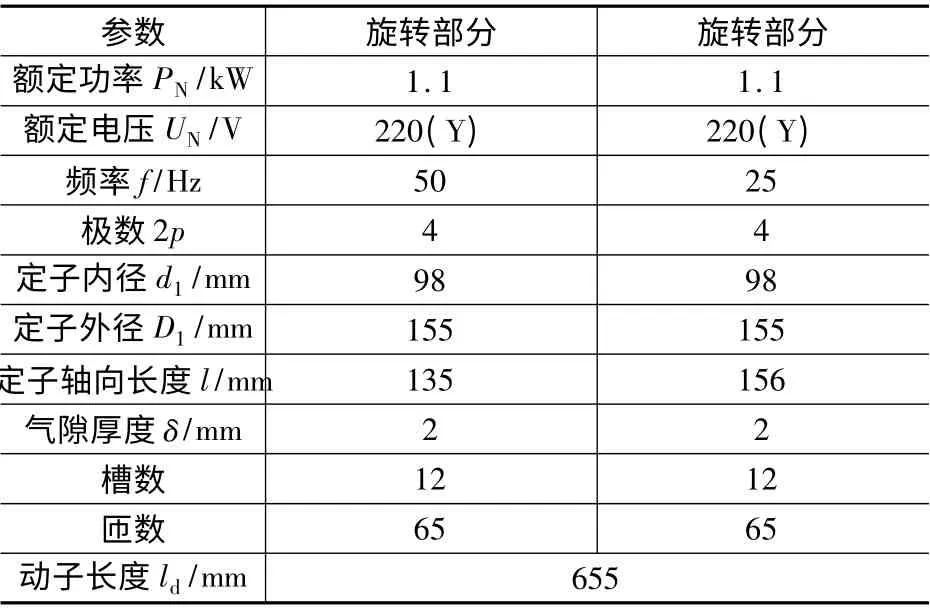
表1 电机主要参数

2 运动耦合理论分析

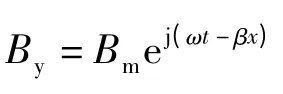
图2 电机磁场的三维计算模型

当动子仅作旋转运动时，V =Vxi 与一般旋转电机相同。它将在动子中感应电势ez，电流iz及电枢反应磁通Bx，动子电流iz将建立矢量磁位Az;当动子仅作直线运动时V =Vzk，在动子中，将产生电势ex，电流ix相应地建立矢量磁位Ax，由矢量磁位Ax产生相应的磁通Bz，电磁力Fx且Fx的方向与Vz相反，起制动作用;当动子作螺旋运动时，V = Vxi +Vzk。其电磁现象应视为上述运动叠加的结果。除了产生ex，ez外，还将产生电势ey，电流iy建立矢量磁位Ay，通过上述分析，动子作螺旋运动时，在动子铁磁体内存在三维矢量磁位A =Axi +Ayj +Azk，相应的存在三维矢量B，J 和H 等。

由麦克斯韦方程组及矢量磁位A的定义，B =∇×A 及∇·A =0。在工频时，忽略位移电流的影响，则可以导出:

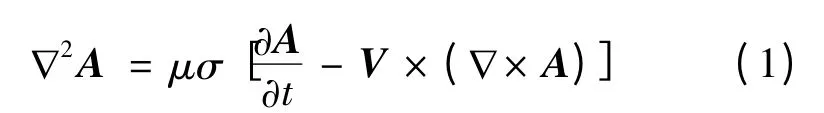
根据式(1)可以将约束磁场的拉普拉斯方程和泊松方程求解归结为对二阶常系数线性微分方程的求解，结合边界条件得出积分常量，求出气隙和动子铁心中的矢量磁位:

在气隙中，A1=A1xi+A1yj+A1zk

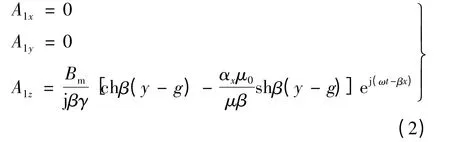
在动子中，A2=A2xi+A2yj+A2zk

当动子仅以Vx作旋转运动时(令Vz=B2z=A2x=A2y=0)，得到电磁力Fx=Fxxi+Fxyj:

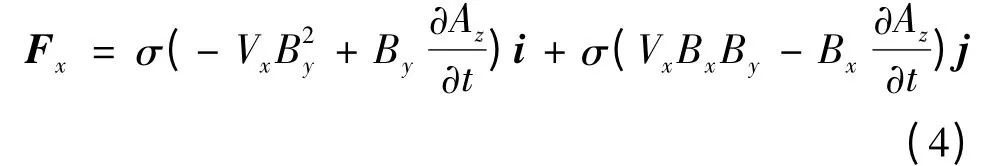
当动子仅以Vz作直线运动时(令Vx=B2x=A2z=A2y=0)，可得电磁力Fz=Fzyj+Fzzk:

当动子作螺旋运动时，由于直线运动速度Vz的影响引入了直线运动与旋转运动二者的相互作用。除了产生上述Fx，Fz意外，还将产生电磁力密度ΔF=ΔFxi+ΔFzk:将已求得的动子中矢量磁位和磁感应强度的表达式代入ΔF 的表达式中，得到:

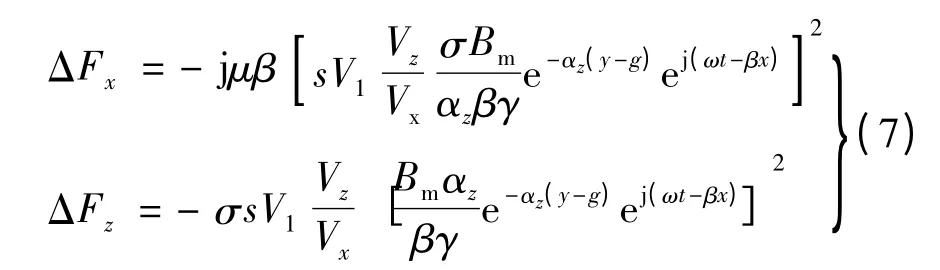
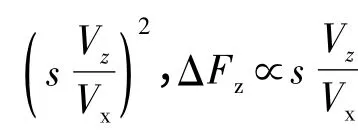
3 有限元建模仿真分析

解析法只是在忽略很多因素下的理想条件下的结果，二维仿真则是考虑了一定的因素，比如端部效应等。但对于两自由度直驱感应电机的特殊结构和多自由度运动形式，三维仿真应该是计算精度最高的，因为三维仿真考虑了很多因素，如绕组端部磁场、旋转运动和直线运动之间的耦合影响。故本文主要采用三维参数化建模来仿真分析两自由度直驱感应电机。建立所有组合情况下的有限元模型仿真，其中一种三维有限元模型如图3 所示。

图3 有限元模型和磁通密度分布

4 仿真结果

为了验证旋转速度分量的引入对直线运动部分的影响，进行如下仿真设置:直线运动部分定子绕组通以线电压220 V，频率5 Hz 的三相交流电，并以轴向平移速度为0.2 m/s 的速度驱动，旋转运动部分定子绕组不通电且旋转速度分别为0，900(°)/s，2 250 (°)/s，4 500 (°)/s，9 000 (°)/s 的速度驱动时，仿真分析不同旋转速度对直线运动部分轴向推力的影响。不同旋转速度下轴向推力随时间的变化情况如图4(a)所示，不同旋转速度情况下稳态轴向推力平均值如图4(b)所示。可见随着旋转速度的增加，其对直线部分轴向推力的影响越来越大，表现为轴向推力越来越来小。

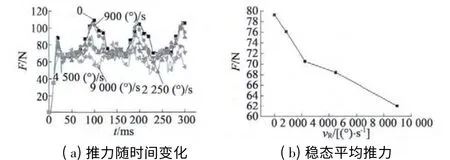
图4 不同旋转速度对直线运动部分的影响

类似的，为验证直线速度分量的引入对旋转运动部分的影响，进行如下仿真设置:旋转部分定子绕组通以线电压220 V，频率5 Hz 的三相交流电，并以轴向平移速度为225 (°)/s 的速度驱动，直线运动部分定子绕组不通电且轴向平移速度分别为0，0.4 m/s，0.8 m/s，1 m/s 的速度驱动时，仿真分析不同轴向平移速度对旋转运动部分转矩的影响。不同轴向平移速度下旋转运动部分转矩随时间的变化情况如图5(a)所示，不同轴向平移速度情况下稳态转矩平均值如图5(b)所示。

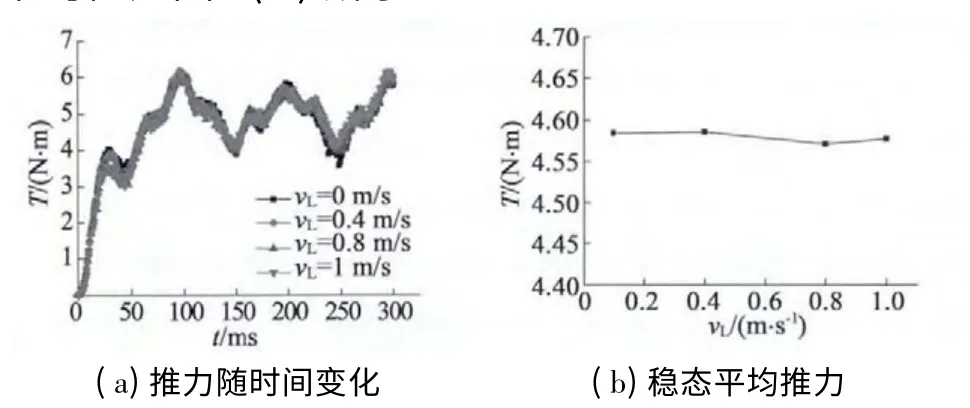
图5 不同轴向平移速度对旋转运动部分的影响

可见，随着轴向平移速度的增加，其对旋转运动部分转矩的影响并不大，转矩变化也很小。这是因为轴向运动速度相对于旋转运动速度太小且转差率太小的原因。根据式(7)可得ΔFx∝ ( sVz/Vx)2即ΔFz∝sVz/Vx。所以直线运动对旋转运动的耦合影响会在直线运动速度Vz很大时才会表现得很明显。而当Vz相对于Vx很小时，A2x，A2y，E2x和E2y近似为0，此时运动耦合影响很小，可以忽略不计。

5 结 语

针对两自由度直驱感应电机的复杂结构和多运动形式，本文采用简化分析的等效平板模型，并依据麦克斯韦方程组三维运动耦合分析模型，并建立相应的三维有限元参数化模型进行仿真分析，得出如下结论:

采用三维有限元分析法，建立三维结构模型才能相对精确地考虑到动子做螺旋运动时，旋转运动部分和直线运动部分之间的相互影响，并验证了所述两自由度直驱感应电机结构的可行性。

对于旋转运动与直线运动之间的运动耦合影响，由于所述电机主要工作于高速旋转低速行进的螺旋运动，故运动耦合影响主要表现为旋转运动对直线运动部分的力能参数的削弱影响。

后续工作将进一步对运动耦合效应和磁场耦合效应进行定量分析，以更精确地实现相应的补偿控制策略。制作试验样机测试平台以及设计控制系统，进而对电机特性作深入的研究。

［1］ 司纪凯，司萌，封海潮，等.两自由度直驱电机的研究现状及发展［J］.电工技术学报，2013，28(3):97 -107.

［2］ MEESSEN K J，PAULIDES J J H，LOMONOVA E A.Analysis of a novel magnetization pattern for 2 - DOF rotary - linear actuators［J］.IEEE TRANSACTIONS ON MAGNETICS，2012，48(11):3867 -3870.

［3］ TURNER Ar，RAMSAY K，CLARK R，et al. Direct -drive rotary-linear electromechanical actuation system for control of gearshifts in automated transmissions［C］//IEEE Vehicle Power and Propulsion Conference，2007:267 -272.

［4］ SZABO L，BENTIA I，RUBA M. A rotary -linear switched reluctance motor for automotive applications［C］//2012 20th International Conference on Electrical Machine(ICEM)，2012:2615 -2621.

［5］ BOLOGNESI P，PAPINI E.FEM modeling and analysis of a novel rotary-linear isotropic brushless machine［C］//International Conference on Electrical Machines(ICEM)2010:1179 -1183.

［6］ AMIRI E，GOTTIPATI P，MENDRELA E A.3 -D space modeling of rotary-linear induction motor with twin-armature［C］//IEEE International Conference on Electric Machines ＆ Drives，2011:202 -206.

［7］ AMIRI E，JAGIELA M，DOBZHANSKI O，et al.Modeling dynamic end effects in rotary armature of rotary - linear induction motor［C］//IEEE International Conference on Electric Machines ＆Drives，2013:1088 -1091.

［8］ 宁玉泉，唐孝镐，黄念森.螺旋运动实心转子异步力矩电机的电磁理论与设计问题［J］. 电工技术学报，1986，1(3):42 -46.

［9］ 张明玉，林金明，唐孝镐.基于三维磁场解析求解的复合转子异步电机的端部系数计算［J］. 电工技术学报，1993，8(1):1-4.

［10］ 司纪凯，艾立旺，韩俊波，等. 直线感应电机空载速度特性分析［J］.电机与控制学报，2014，18(7):37 -43.

［11］ 司纪凯，艾立旺，司萌，等. 两自由度直驱感应电动机的特性分析［J］.微特电机，2014，42(8):1 -4.

［12］ 司纪凯，司萌，封海潮，等. 转子导电材料和气隙对直线弧形感应电机性能影响［J］. 电机与控制学报，2012，16(10):31-37.

［13］ 司纪凯，韩俊波，艾立旺，等. 空心转子弧形直线感应电机的优化与特性分析［J］.微特电机，2014，42(5):48 -52.