改进的变步长LMS自适应滤波算法

刘小东，黄洪琼

(上海海事大学信息工程学院，上海201306)

0 引言

最小均方误差 (LMS)算法由Widrow和Hoff提出，随着理论的推广及深入，自适滤波技术广泛应用于自动控制、雷达通信、系统辨识等智能信息处理领域 (见图1)。

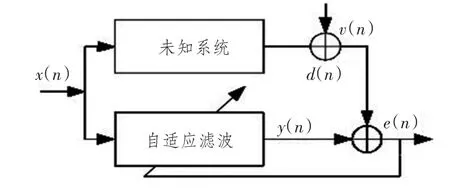
图1 自适应滤波系统Fig.1 Adaptive filtering system

LMS算法的优点是计算量不大，易实现，只需知道自适应线性组合器每次迭代运算组合的输入激励及参考响应，那么选用自适应LMS算法将很适合。LMS算法的主要缺陷是收敛速度、时变系统跟踪速度与稳态误差方面的矛盾得不到很好的解决。针对这一缺点，人们提出很多改进的LMS算法，而变步长 LMS算法［1－9］是目前应用最广泛的一类算法，这些算法的区别在于变步长的改变机制不同。

基于变步长的调整机制［1］，有的提出一种时间平均估值梯度的自适应滤波算法［2］，有的提出一种变步长归一化的自适应滤波算法［3］，又有基于估值误差大小来调整步长因子的自适应滤波算法［4］。文献［5］提出迭代次数与步长成反比的自适应滤波算法，该算法能得到较小的稳态失调，但不具备时变跟踪能力。文献 ［1］提出了变步长调整规则的自适应滤波算法 (SVSLMS)，即系统初始阶段或未知系统时变阶段步长较大，使算法有较快的收敛速度，随着收敛速率的不断深入，逐渐更新步长使其减小以达到较小的稳态偏差。然而，SVSLMS算法在误差接近零处变化时，不具有缓慢变化的特征，使得SVSLMS算法在稳态时仍有较大的步长变化。为此，文献［6］提出了改进的SVSLMS算法，使其在稳态时步长因子μ较小，但仍然未较好的改善SVSLMS算法的收敛速度和稳态偏差等性能指标［10－11］。收敛速度，时变跟踪速度及稳态误差是评判LMS自适应滤波算法优劣的重要技术指标。如何有效的设计步长因子μ(n)与e(n)的映射函数关系，是解决算法收敛速率、时变系统跟踪能力与稳态误差矛盾之间的关键技术。

1 新的变步长LMS滤波算法

根据文献［1］提出的变步长指导调整规则，本文给出一种变步长调整自适应滤波算法的通式，并通过实验仿真求解最佳指数因子。

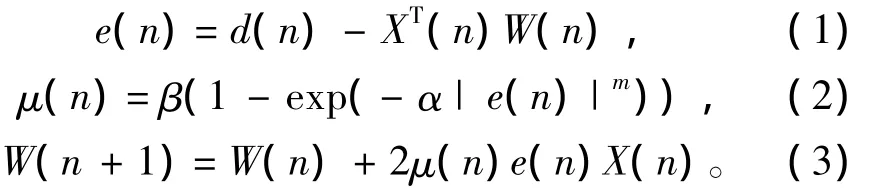
式中:W(n)=［w(n)，w(n－1)，w(n－2)，…，w(n－L+1)］T为自适应滤波器在时刻 n的权重矢量;X(n)为输入激励矢量;d(n)为期望响应值;v(n)为干扰噪声;e(n)为误差噪声;L为滤波器的阶数;μ(n)为步长因子，它控制着算法的稳定性和收敛速度;α为控制关于e(n)是u(n)的函数形状的常数;β为控制步长因子取值范围的参数(0＜β＜1/λmax)。最佳的α和β由实验仿真获得，当然α和β的选取在满足LMS算法收敛的前提下，收敛的条件是步长因子μ(n)不超过输入激励矢量自相关矩阵特征值的最大值λmax。

图2 为β=0.2，α=50，m=1，2，3，4，6时，式(2)步长因子u(n)关于误差e(n)的函数曲线簇。当m=1时，即为文献［1］提出的 u(n)是 e(n)的Sigmoid函数，当误差e(n)在零附近处变化时，此时算法已达到稳态，u(n)波动较大，不具有缓慢变化的特性;当m=2时，即为文献［6］提出改进的SVSLMS算法，当算法达到稳态时，仍未较好改善文献［1］中u(n)缓慢变化的特性;当m=3时，在算法的初始收敛阶段和跟踪阶段，u(n)随e(n)的增大而自动增大，在e(n)接近0时或将达到稳态时，u(n)仍然具有缓慢变化的特性;当m=2时，曲线的底部形态比m=3的曲线底部形态凸起，说明误差e(n)在接近零处变化时，此时算法已达到或将要达到稳态时，u(n)仍然变化较大，此时意味着m=2并不是最优的指数缓慢变化因子;当m=4和m=6时，虽说曲线底部的变化更加平缓，但在误差e(n)还未到达稳态或还未接近零处变化时，步长因子u(n)早已归0，这将促使更大的稳态偏差。

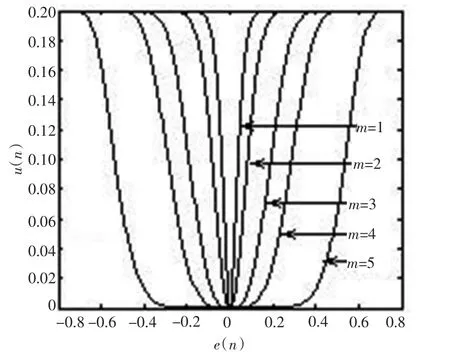
图2 m=1，2，3，4，6时，误差与步长的关系曲线Fig.2 m=1，2，3，4，6，the error curve with step size

2 确定指数因子

另外，在未确定最优的指数缓慢变化因子前，在多次试验基础上选取2～3之间具有代表性数据m=2.5，2.75，3来分析所对应算法的稳态性能(系统收敛的前提下，0＜μ＜λmax，λmax是输入激励矢量自相关矩阵的最大特征值)。理论分析和计算机试验仿真结果表明，m=2.85～3.15之间取值时，算法技术指标的性能比较好。如图3所示，在α和β取值一定的情况下，3种曲线底部特性的平缓度是不同的，m=2比m=2.75凸起，m=2.75比m=3凸起，这就说明在e(n)接近0处时，m=3曲线的底部比m=2.75和m=2的曲线的底部更具备迟缓变化的特征。在本文中取m=3时，具有最优指数缓慢变化因子特征。

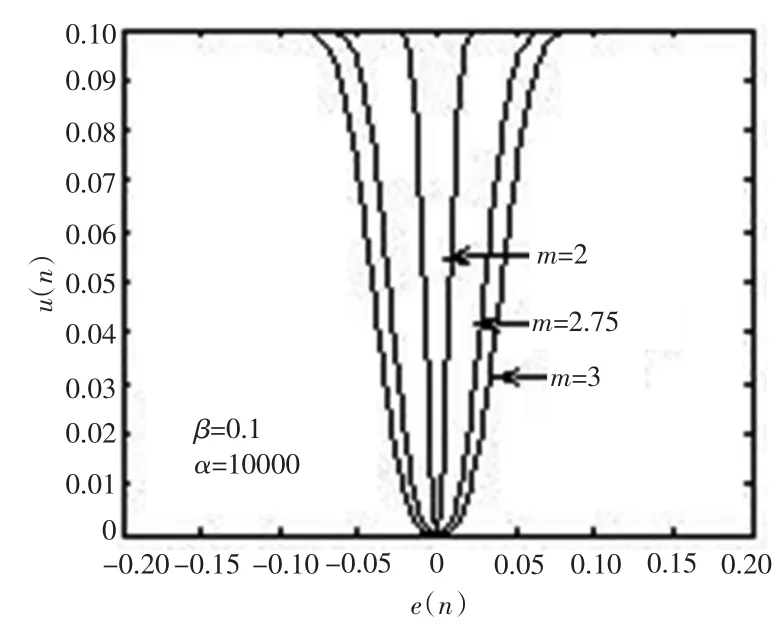
图3 m=2，2.75，3曲线形态比较Fig.3 m=2，2.75，3 curve shape comparison

在相同实验条件下，3种算法的收敛速度相当，如图4所示。但就算法稳态失调相比，m=3所对应的稳态误调噪声最小。这是因为在m=3对应的算法中，很小的e(n)对应很小的u(n)，在m=2和m=2.75对应的算法中很小的e(n)则对应很大的u(n)，所以m=3对应的稳态误差噪声要比m=2.75和m=2所对应的稳态误差噪声小，这一点在图4的仿真实验中得到验证。

分析至此，本文最优的指数缓慢变化因子取m=3，得出最佳变步长公式为:

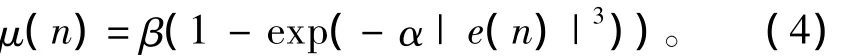
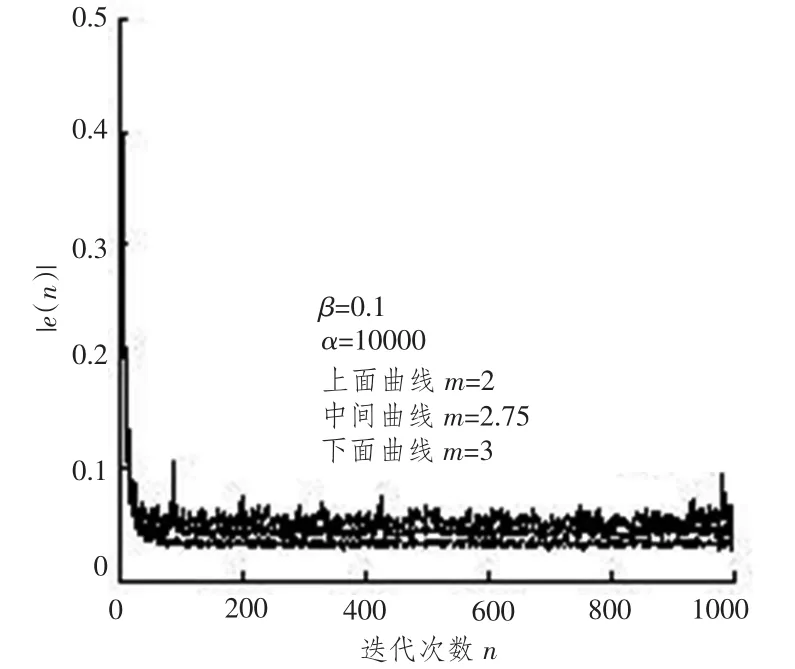
图4 m=2，2.75，3曲线的稳态误差比较Fig.4 m=2，2.75，3 comparison of steady-state error curve

3 实验结果及分析

采用与文献［1］相同的实验条件:

1)采用2阶的自适应滤波器;

2)已知W*=［0.8，0.5］T为未知系统FIR的系数，在第500个采样点时刻，时变系统发生突变，FIR权矢量系数变成W*=［0.4，0.2］T;

3)x(n)是方差为1，均值为0的高斯白噪声;

4)v(n)是方差为0.04，均值为0的高斯白噪声，且与x(n)不相关;

为得出每条实验仿真曲线，独立进行200次实验，每次实验采样点数均为1 000。然后求取统计平均，得出平均学习曲线。

图5是α=500固定，β变化时算法的收敛曲线，β值分别取0.01，0.03，0.06，0.2，随着β的增大(当然在满足算法收敛的前提下0＜β＜1/λmax)，算法的收敛速度逐渐提高，当β增到一定限度时，收敛速率不再提升，实验结果显示，最佳β取值0.2。

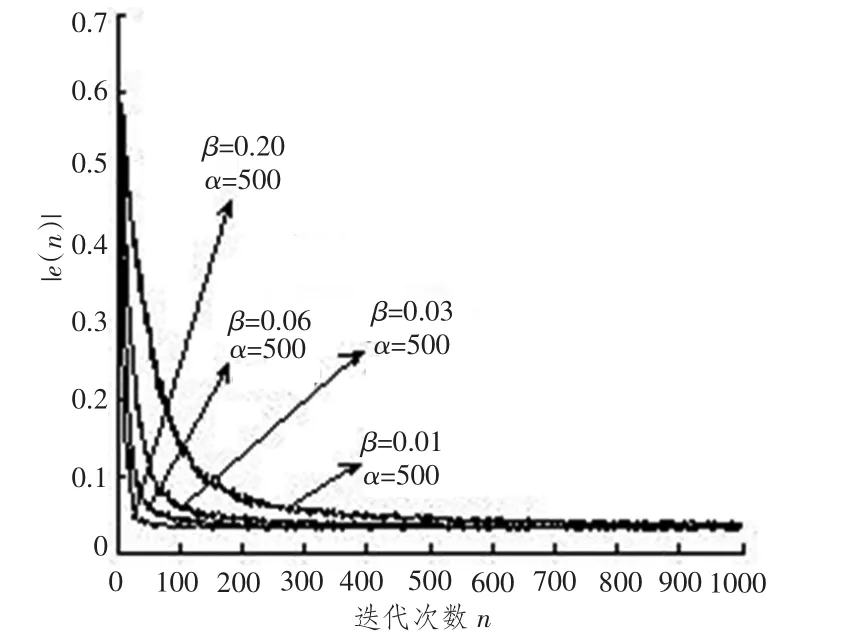
图5 α=500，β变化的曲线Fig.5 α =500，βcurve changes

图6是β=0.2固定，α值变化的算法收敛曲线，α值分别取1，10，100，10 000，算法的收敛曲线，同理α增大到一定程度，算法收敛速度不再增加，本实验条件下最优的α值为10 000。

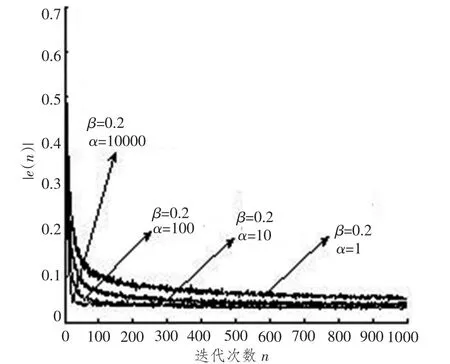
图6 β=0.2，α变化的曲线Fig.6 β=0.2，αcurve changes

通过获取最佳的指数因子m及最优的控制参数α和β之后，采用文献［1］相同的实验条件，实验仿真结果如图7所示，本文算法与SVSLMS算法及文献［6］中改进的SVSLMS算法的对照，本文算法最佳α =10 000，β=0.2，文献［1］中SVSLMS算法的最佳参数α和β分别值取为1.0和1.5。文献［6］中改进的SVSLMS算法的最佳参数α和β分别取20和0.2。由图7对比可看出，本文算法的收敛速度明显快于SVSLMS算法和文献［6］改进的SVSLMS算法，且在第500个采样点未知系统发生突变时刻，本文算法的时变跟踪能力和稳态失调比SVSLMS算法和文献［6］的算法更优越，这说明本文算法具备更好的收敛速度，系统时变跟踪能力，稳态失调技术指标。

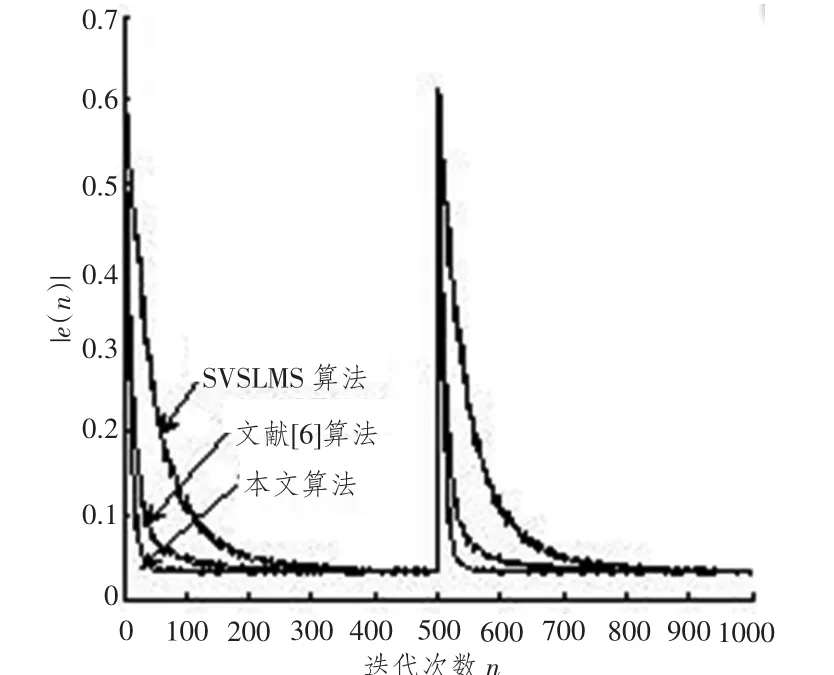
图7 实验仿真结果对照Fig.7 Simulation results comparison

4 结语

通过改进步长因子u(n)与误差信号e(n)之间的非线性函数关系，给出了误差信号e(n)的指数因子变化的通式，经试验仿真最佳指数缓慢变化因子的分析过程，提出了一种新的变步长算法。该算法具备初始阶段和未知体系时变阶段步长很大，而算法到达稳态阶段步长较小的转变，且克服了SVSLMS算法在稳态阶段步长起伏波动较大的缺点，提高了算法的鲁棒性，同时比文献［6］改善的SVSLMS算法具备更快的收敛速率和时变跟踪速率。

［1］ 覃景繁，欧阳景正．一种新的变步长LMS自应用滤波算法［J］．数据采集与处理，1997，12(3):171 －174．TAN Jing-fan，OUYANY Jing-zheng．A new variable steps size LMSfiltering algorithm［J］．Journal of Data Acquisition and Processing，1997，12(3):171 －174．

［2］ MAYYASK，MOMANI F．An LMSadaptive algorithm with a new step － size control equation［J］．Journal of the Franklin Institute，2011，348(4):589 －605．

［3］ ZHANG Z，ZHANGD．New variable step size LMSadaptive filtering algorithm and its performance analysis［J］．Systems Engineering and Electronics，2009，31(9):2238 －2241．

［4］ ABOULNASR T，MAYYAS K．A robust variable step-size LMS-type algorithm:analysis and simulations［J］．Signal Processing，IEEE Transactions on，1997，45(3):631 －639．

［5］ GITLIN R D，MAZO J E，TAYLOR M．On the design of gradient algorithms for digitally implemented adaptive filters［J］．Circuit Theory，IEEE Transactions on，1973，20(2):125－136．

［6］ 高鹰，谢胜利．一种变步长LMS自适应滤波算法及分析［J］．电子学报，2001，29(8):1094 －1097．GAOYing，XIE Sheng-li．A variable step size LMSadaptive filtering algorithm and its analysis［J］．Acta Electronica Sinica，2001，29(8):1094 －1097．

［7］ MAYYASK，MOMANI F．An LMSadaptive algorithm with a new step － size control equation［J］．Journal of the Franklin Institute，2011，348(4):589 －605．

［8］ HUANG H C，LEE J．A new variable step-size NLMS algorithm and its performance analysis［J］．Signal Processing，IEEE Transactions on，2012，60(4):2055－2060．

［9］ Wei A，Wan － Qin X，You － Peng Z，et al．A new variable step size LMS adaptive filtering algorithm［C］//Computer Science and Electronics Engineering(ICCSEE)，2012 International Conference on．IEEE，2012:265 －268．

［10］ CHAN S C，CHU Y J，ZHANG Z G．A new variable regularized transform domain NLMS adaptive filtering algorithm—acoustic applications and performance analysis［J］．Audio，Speech，and Language Processing，IEEE Transactions on，2013，21(4):868 －878．

［11］ REN Z Z，XU J C，YAN Y P．Improved variable step size LMSadaptive filtering algorithm and its performance analysis［J］．Jisuanji Yingyong Yanjiu，2011，28(3):954 －956．