纵向轻围壁屈曲对船体总纵强度影响分析

王西典，张世联

(上海交通大学船舶海洋与建筑工程学院，上海200240)

0 引言

船体结构在发生总纵弯曲时，受压构件常常会因为受压过度而丧失稳定性，从而大大降低船体抵抗总纵弯曲的能力。因此，在船体总纵强度设计中，必须考虑受压构件的稳定性，并分析构件屈曲后的应力再分配，以正确反映船体总纵强度的承载能力。

目前各类船舶出于总布置分舱和防火的需要，常需在船体内设置钢质纵向轻围壁。此类围壁在船体梁总纵弯曲时，一般处于受压或受拉状态，特别对于远离船体梁中和轴的受压纵向围壁，其稳定性需要引起足够重视。另外，此类纵向轻围壁并非总是在船长范围内连续，为了能准确的反映其参与的总纵弯曲的程度，可以通过有限元直接计算或采用梁的弯曲理论计算其受压或受拉状态，并对其进行进行稳定性分析。

目前对于板格的屈曲校核，中国船级社 (CCS)在《钢质海船入级规范》中不考虑其屈曲后的承载能力［1］;CSR共同规范中提出了计算板格后屈曲承载能力的方法，需计及载荷在板格上的重新分布从而得到板格的极限承载能力［2］。然而，CSR共同规范并没有针对该方法提出完整的计算公式［3］，出于安全的考虑，仅计及板格的有效承载宽度来考虑其后屈曲承载能力，也未计及板格屈曲对相邻构件应力分布的影响。

本文以一设置多道纵向轻围壁的某船船体为研究对象，参考中国船级社 (CCS)《钢质海船入级规范》和CSR共同规范，采用全船有限元方法［4］对其进行船体总纵强度及屈曲强度分析研究，特别是对纵向轻围壁的后屈曲能力分析。本文通过对纵向轻围壁加筋板格的屈曲强度、后屈曲能力和纵向轻围壁屈曲对船体总纵强度影响进行分析，提出的纵向轻围壁加筋板格屈曲后的船体总纵强度分析方法可供船舶设计部门参考。

1 全船有限元模型总纵强度计算

研究的船体总长180 m，型宽26.0 m，型深15 m。在船体上部设置有多道纵向轻围壁，其纵向轻围壁的结构型式均为横骨架式，全船有限元模型和船中典型横剖面示意图如图1和图2所示。

图1 有限元模型Fig.1 Finite element model

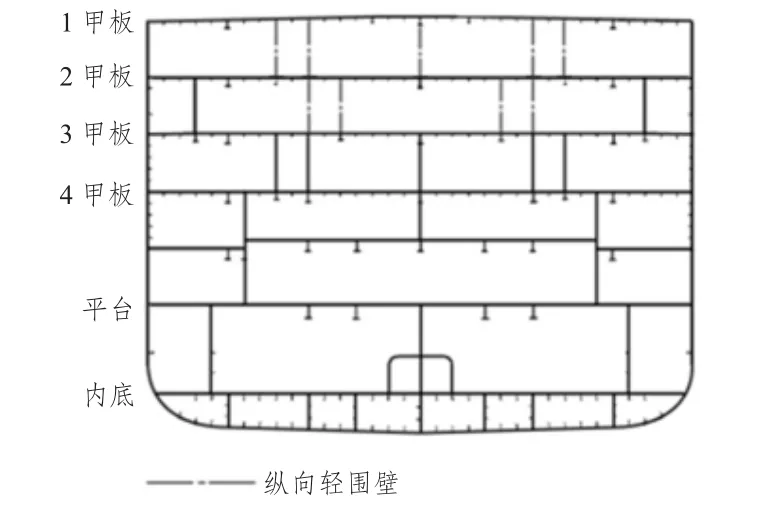
图2 船中典型横剖面Fig.2 Typical mid-ship section

全船有限元分析时采用设计波法计算该船的总纵强度，通过分析，该船总纵强度满足规范要求。

评估该船纵向轻围壁的屈曲强度，需选择最不利的中垂状态进行分析。该船最大中垂弯矩M=－6.28×108N·m，纵向轻围壁在中垂状态下的总纵弯曲应力分布如图3和图4所示。

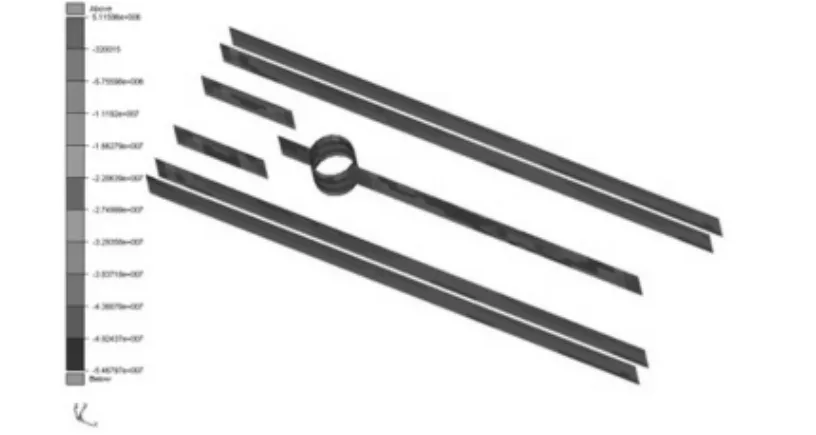
图3 1甲板下纵向轻围壁应力Fig.3 Stress of longitudinal partition bulkhead under deck 1

图4 2甲板下纵向轻围壁应力Fig.4 Stress of longitudinal partition bulkhead under deck 2

2 纵向轻围壁屈曲强度分析

2.1 屈曲强度评估准则

2.1.1 CCS规范屈曲评估

CCS《钢质海船入级规范》在总纵强度中对板格屈曲强度作了明确规定，校核板格的工作应力σx应不大于板格的临界屈曲应力σcr。计算板格的理想弹性屈曲应力σE可按下式进行:

由于校核板格为横骨架式结构，理想弹性屈曲应力σE较小，故不必进行弹塑性修正，其临界屈曲应力 σcr=σE。

规范在结构强度直接计算中，考虑到板格复杂受力情况对其屈曲强度的影响，校核板格的屈曲安全因子λ应不小于1。对于承受双向压缩与剪切的板格，可按下式计算其屈曲安全因子:

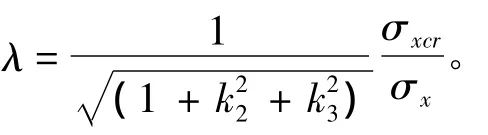
2.1.2 CSR共同规范屈曲评估

CSR共同规范对板格的屈曲校核引入折减系数，考虑了板格边界刚性扶强材的带板，可表征板格的有效承载宽度，用折减因子κ表示。每个基本板格均应符合以下衡准:

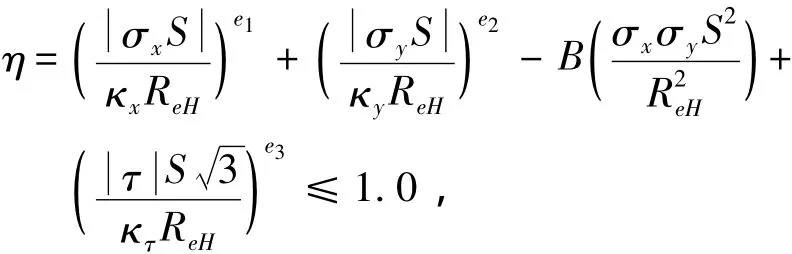
同时，每个板格需满足以下公式:

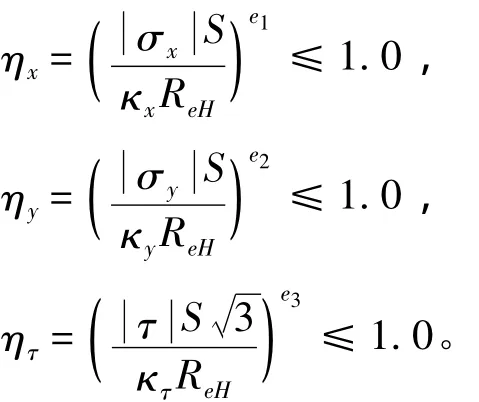
2.2 纵向轻围壁屈曲强度评估

根据中垂状态计算结果，在典型横剖面中和轴以上的纵向轻围壁板单元处于受压状态。通过对受压纵向轻围壁屈曲强度的分析，船中附近区域内的1甲板下纵向轻围壁和2甲板下纵向轻围壁不满足规范的屈曲强度要求。依据CCS规范和CSR共同规范屈曲强度评估准则，表1给出船中剖面上述纵向围壁的屈曲校核结果。

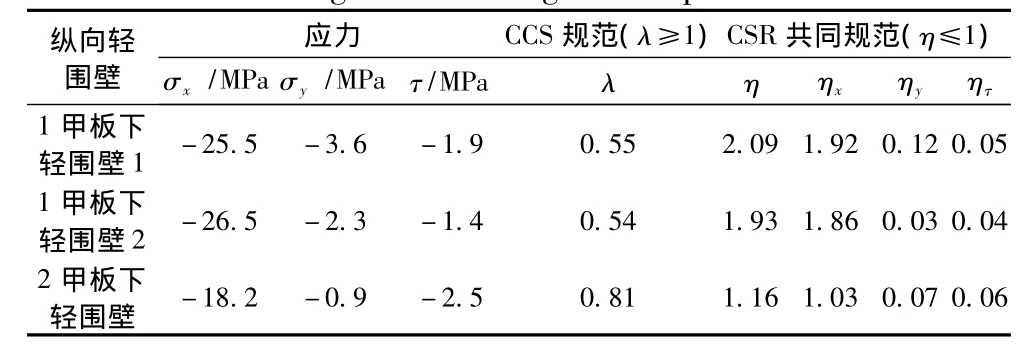
表1 纵向轻围壁屈曲校核Tab.1 Buckling check of longitudinal partition bulkhead

2.3 满足屈曲强度衡准的加强方案

对不满足CCS规范和CSR共同规范屈曲强度衡准的纵向轻围壁，采用增加板厚或设置加强筋 (扁钢)的加强方案 (见表2)。通过计算，该加强方案可以满足规范屈曲强度衡准。

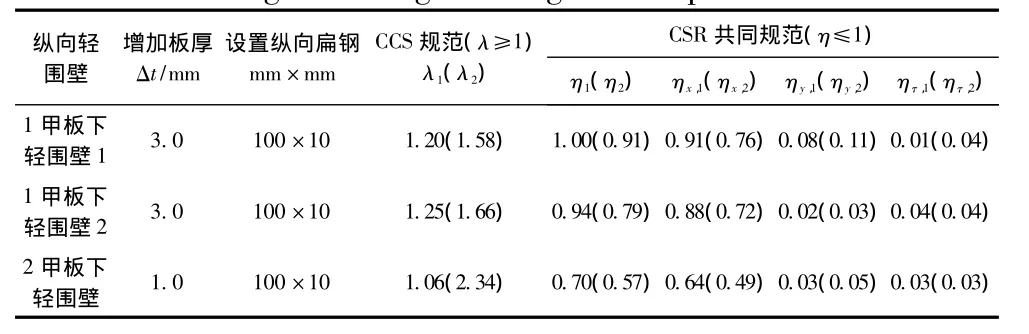
表2 纵向轻围壁加强方案Tab.2 Strengthen design of longitudinal partition bulkhead

2.4 纵向轻围壁屈曲强度讨论

1)CCS与CSR两种规范对纵向轻围壁板临界屈曲应力的计算及屈曲强度的评估均没有涉及到其屈曲后对总纵强度的影响，即在部分纵向轻围壁屈曲的情况下，船体总纵强度还能否满足要求;

2)CCS与CSR两种规范对屈曲围壁板加强的规定较为严苛，特别在船体总纵强度已满足衡准的条件下，通过增加板厚或增加加强筋来保证其屈曲强度，会导致总纵强度过剩，同时也增加了船体重量，这与结构理性设计理念［6］相悖;

3)实际上加筋板格屈曲后仍有一定的承载能力，即加筋板格的后屈曲承载能力［5］。为此，在船体总纵强度分析中，对屈曲的纵向轻围壁，可以按加筋板格的后屈曲理论［6］对其进行减缩，采用逐步近似法计算分析船体总纵强度［7－8］。

3 纵向轻围壁屈曲后船体总纵强度设计

3.1 加筋板格的后屈曲现象

当载荷超过加筋板格的临界屈曲应力时，应力沿板宽开始自行重新分布。与加强筋相连的有效板宽be内应力较高，板宽的中部应力较低，即发生“退避”现象。随载荷增加，板两侧的最大应力会迅速增加，直至达到屈服应力发生崩溃为止，如图5所示。

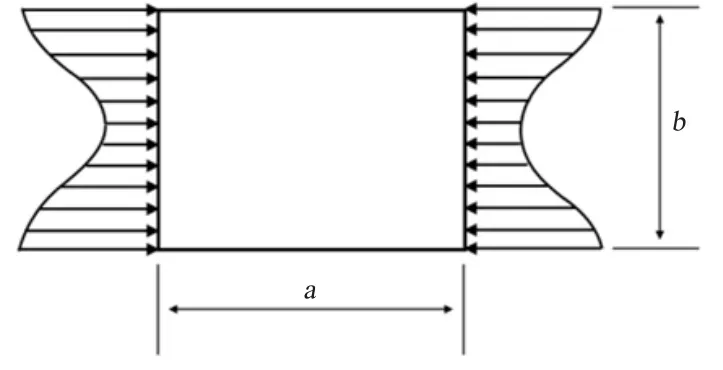
图5 加筋板屈曲后的应力分布Fig.5 Stress distribution of post-buckling plate

在船体总纵强度设计中，应考虑到加筋板格的后屈曲现象。对于发生屈曲的柔性板，应在总纵强度计算中对其进行折减［7］。在实用中，可用图6的形式代替图5中的真实应力分布，有效板宽be以外的部分承受临界屈曲应力σcr，该部分面积需进行折减计算。对应于板格的极限承载状态，可将其视作板格的后屈曲承载状态，称为屈曲状态1。为了保持原来剖面上压力值不变，折减板格应保持下列关系:

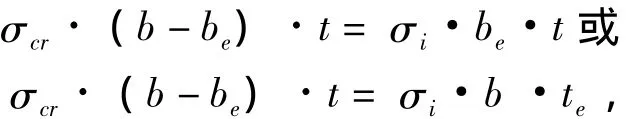
式中:A为受折减部分的实际剖面积;te，be和A'分别为折减后的相当宽度、相当厚度和相当面积。

定义折减系数φ为折减后相当面积与实际面积之比，φ=A'/A=σcr/σi。

考虑板格的极限承载状态，由于板格屈曲后板边的应力远大于板中的应力，可假设板的荷重全部由临近板边的有效板宽部分来承受，此时相当于折减系数φ=0，称为屈曲状态2，如图7所示。

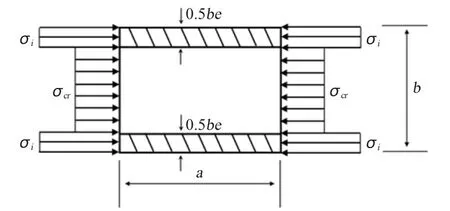
图6 加筋板屈曲后的简化应力分布Fig.6 Simplified stress distribution of post-buckling plate

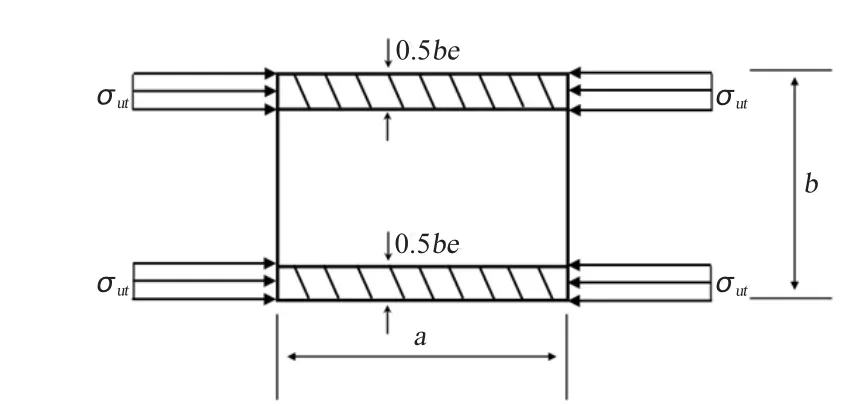
图7 加筋板极限承载状态的应力分布Fig.7 Stress distribution of plate at ultimate state

3.2 加筋板格屈曲后的有效板宽计算

根据板在屈曲后压应力的分布规律，可以计算板的有效宽度be。有效宽度随板所受的压力大小而变化，给实际使用造成一定的困难。

对应屈曲状态1，在实用中可使用巴普考维奇(П.Ф.Попко － вич)提出的近似公式进行计算，有效板宽等于板格短边长度的0.44倍［5］。

对应屈曲状态2，在板格的极限承载状态下，卡门(V.Karman)提出有效板宽与板的柔度系数有关［9］。

定义板的柔度系数

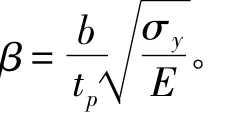
Faulkner根据卡门的研究结果，经过大量实验，得到板格极限承载状态下的有效板宽计算公式［10］:

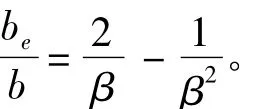
上述公式计算有效板宽时考虑了板格不同的屈曲状态，故计算结果有一定差异。巴普考维奇近似公式的计算结果大于Faulkner公式的计算结果。

3.3 纵向轻围壁屈曲后船体总纵强度设计

纵向轻围壁屈曲后，其承受的部分载荷将转移到与之相连的刚性构件上去，导致船体结构的总纵强度发生变化。考虑到加筋板格的后屈曲现象，应对屈曲围壁板进行折减，采用逐步近似计算法计算船体总纵强度。

逐步近似计算法要求对屈曲板格按情况1进行折减，并需比较屈曲板格折减前后主要刚性构件的应力差值。若折减前后的应力差值小于5%，可将折减后的总纵强度计算结果作为最终计算结果，在此基础上对船体结构进行屈服强度和屈曲强度评估;若折减前后的应力差值大于5%，应当对屈曲板格重新进行折减计算，若再次计算的结果仍不能满足要求，需对船体结构进行重新设计［11］。按情况2对屈曲板格进行折减是对板格极限承载状态的考虑，即有效板宽以外的围壁板均不参与总纵弯曲，可作为逐步近似计算法计算结果的参考。

在有限元模型中，可对屈曲围壁板的板厚折减，并进行迭代计算;也可采用微分法［11］计算围壁板折减对船体结构总纵强度的影响。

3.3.1 微分法在船体总纵强度设计中的应用

设一剖面模数为

现在此剖面上离中和轴距离为C处增加 (减少)一微面积d F，则剖面模数发生变化。

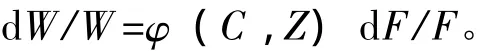
式中:φ (C，Z)=(C/ρ)2+C/Z;ρ2=I/F，F为剖面改变前面积。

若作用于船体的弯矩不变，有多处围壁板需折减时，对离中和轴为Z处的构件内的应力改变则有

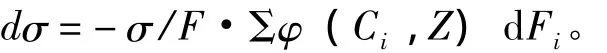
式中:σ为构件原来的应力;d Fi为折减后相当面积与实际面积之差。

3.3.2 船体总纵强度实例计算

采用有限元方法计算围壁板屈曲后船体的总纵强度，对屈曲围壁板折减可分别按情况1和情况2处理。表3列出了船中剖面围壁板的有效板宽be、折减系数φ和相当板厚te的计算结果。

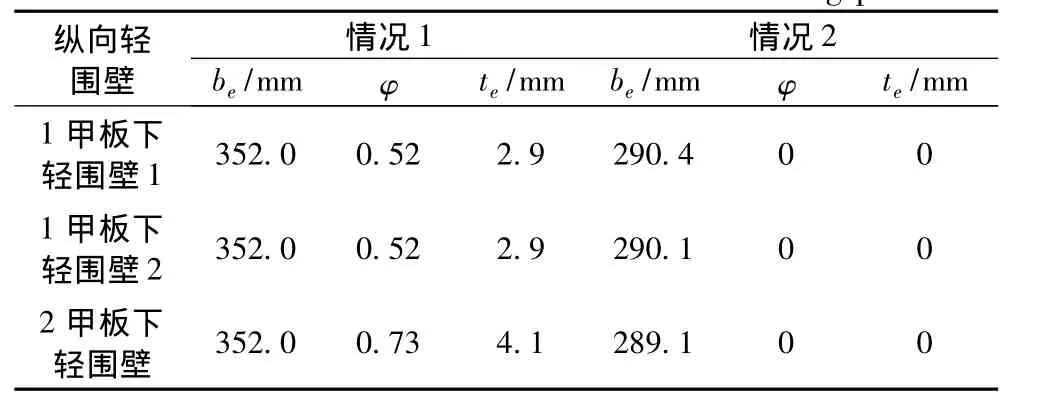
表3 屈曲围壁板折减计算结果Tab.3 Calculation result of reduction in buckling plate

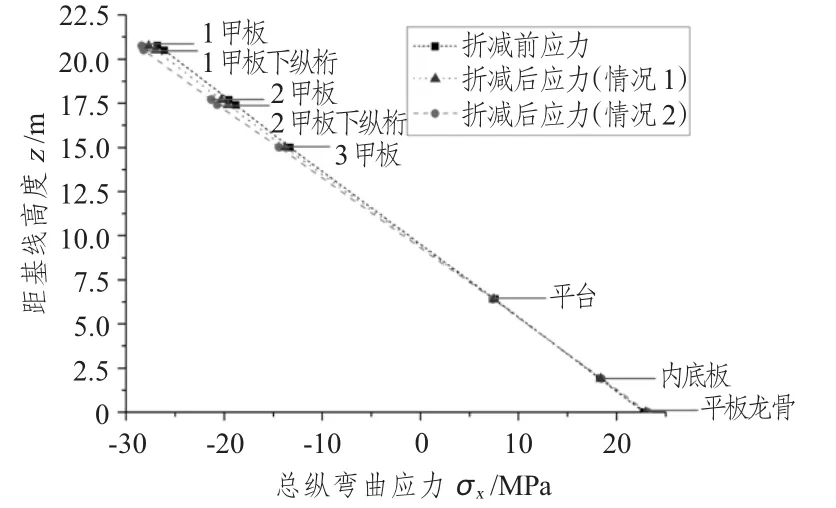
图8 屈曲围壁板折减前后船肿剖面各构件的应力Fig.8 Stress of mid-ship components before and after reduction in buckling plate

图8为屈曲围壁板折减前后船中剖面各构件的应力水平。围壁板折减后，船体结构的总纵强度有所降低，应力水平有一定上升;剖面的应力分布发生变化，尤其与纵向轻围壁直接相连的船体上部结构，应力有较明显的增大;情况2的应力水平高于情况1，这是由于情况2考虑了按情况1逐步近似后可能达到的最危险情况，对船体总纵强度的削弱较大。

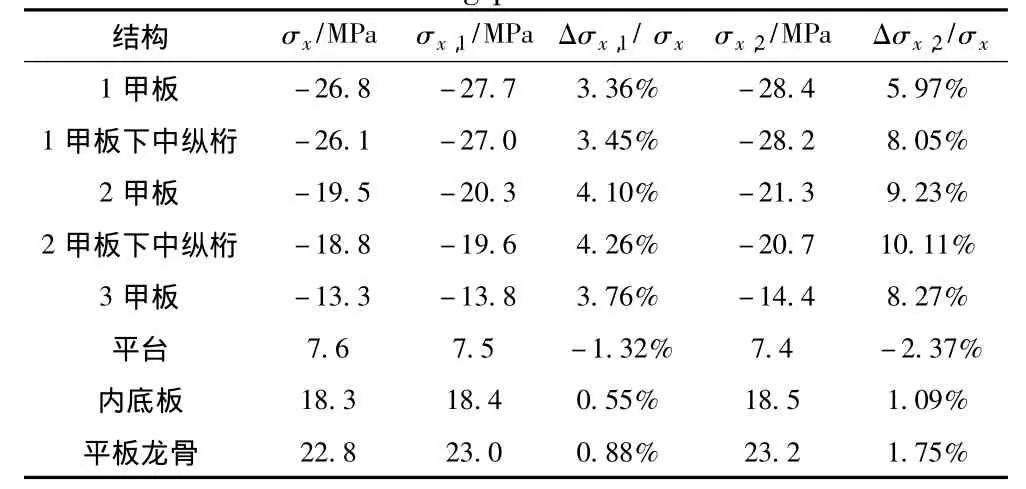
表4 围壁板折减前后船肿剖面各构件应力变化Tab.4 Stress variation of mid-ship components before and after reduction in buckling plate

表4列出了围壁板折减前后船中剖面各构件总纵弯曲应力的变化情况。按情况1折减屈曲围壁板并进行计算，各构件应力变化不超过5%，根据逐步近似计算法的要求，可将此次计算结果作为最终的计算结果。在此基础上对船中剖面进行屈曲强度校核，均满足规范衡准;进行屈服强度校核，最大屈服应力σe出现在1甲板上，且满足强度衡准:

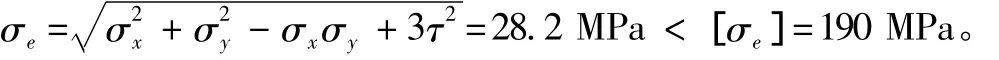
对船体结构的其他剖面均可采用逐步近似计算法进行计算分析，并进行强度评估。计算结果表明，纵向轻围壁屈曲后，船体总纵强度仍满足强度衡准，表明结构是安全的。故不必按规范对轻围壁进行加强，对研究的船体而言，可节省约30～60 t钢材，约占实船结构重量的0.3%～0.6%。

从上述计算过程可看出，有限元计算围壁板屈曲后船体总纵强度的方法较为繁琐，实用中采用微分法可较为简便地计算纵向轻围壁屈曲对船体结构强度的影响。以求解船中剖面1甲板总纵弯曲应力为例，表5给出了微分法的计算结果。

根据有限元计算结果，取1甲板原来的应力σ=－26.8 MPa，运用微分法计算dσ=－0.6 MPa，与有限元计算结果dσ=－27.4－(－26.8)=－0.6 MPa是一致的。在本例中，1甲板总纵弯曲应力满足强度要求，故不必对纵向轻围壁进行加强;若出现不满足强度要求的情况，为了保证原来剖面的强度条件不变，需对折减面积进行补偿，也可采用微分法对相应构件进行加强，以满足强度要求。

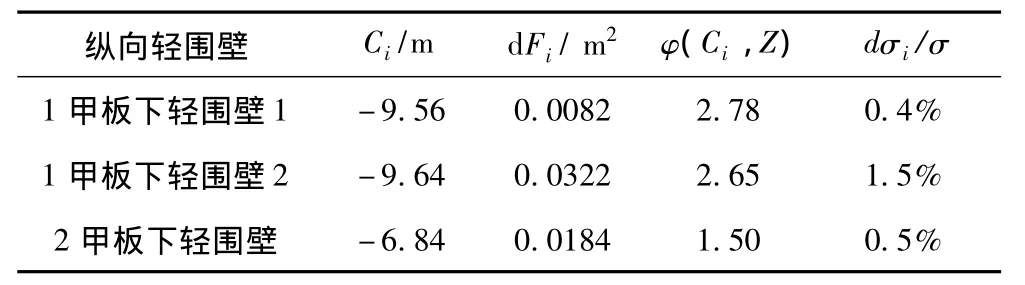
表5 微分法求解1甲板应力Tab.5 Calculation of deck 1 stress in differential method

4 结语

本文对一设有多道纵向轻围壁船舶的总纵强度进行有限元计算，探讨了纵向轻围壁的屈曲对总纵强度的影响，并利用加筋板格的后屈曲理论对其进行了分析和评估，该分析方法可为纵向轻围壁的优化设计提供参考。

［1］ 中国船级社．钢质海船入级与建造规范［M］．北京:人民交通出版社，2012．

［2］ 国际船级协会．双壳油船共同结构规范［M］．中国船级社，译．北京:人民交通出版社，2006．

［3］ 国际船级协会．散货船共同结构规范［M］．中国船级社，译．北京:人民交通出版社，2006．

［4］ 陈庆强，朱胜昌，郭列，等．用整船有限元模型分析方法计算舰船的总纵强度［J］．船舶力学，2004，8(1):79－83．

［5］ 陈铁云，陈伯真．船舶结构力学［M］．上海:上海交通大学出版社，1991．

［6］ HUGHESO F．船体结构设计［M］．张祥孝，译．华南理工大学出版社，1988．

［7］ 杨代盛．考虑剖面减缩后的中剖面设计［C］//中国造船学会论文集，1962．

［8］ GJB/Z 119－99，水面舰艇结构设计计算方法［S］．GJB/Z 119－99．

［9］ VON KARMAN T，SECHLER E E，DONNELL L H．Strengthofthin platesin compression［J］．Trans American Society of Mechanical Engineers，1932，54(5):53 －57．

［10］ FAULKNER D．A review of effective plating for use in the analysis of stiffened plating in bending and compression［J］．JShip Res，1975(19):1 －17．

［11］杨代盛．船体强度与结构设计［M］．北京:国防工业出版社，1982．