参量阵差频波与原频波相位及幅值关系研究

吕良浩，胡德胜

(1．大连测控技术研究所，辽宁 大连116013;2．中国人民解放军91315部队，辽宁大连116041)

0 引言

参量阵是一种非线性声现象的应用，即声波在介质中传播时，波与波的非线性作用会产生与原频波频率不同的差频波与和频波［1］。由于其具有小尺寸、宽频带、窄波束、无旁瓣等优点，因此受到人们的关注并将其广泛应用于水声工程中，最具代表性的是参量阵地层剖面仪和掩埋物探测声呐［2－5］。参量阵理论最初由 Westervelt［6］于1963年提出，之后不久科研人员就意识到了暂态信号参量阵的存在，并发现了参量阵差频信号的自解调效应，其中Moffett做了许多有意义的工作［7－8］。针对如何提高参量阵的转换效率，人们一直对差频波与原频波之间的幅值关系比较感兴趣，而对参量阵差频波的相位与原频波的相位关系未予关心。在参量阵的实际应用中，差频波的相位有时也起很大作用。本文以Moffett参量阵理论为基础，推导出参量阵差频波与原频波之间的相位及幅值的关系，并做相应的实验研究。

1 理论

假设激励信号为:

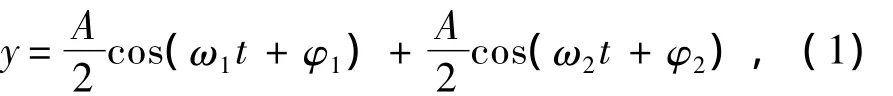
式中:ω1和ω2为角频率，且令ω1＞ω2;φ1和φ2为初相位;为每个稳态信号的幅值。将上式变为:

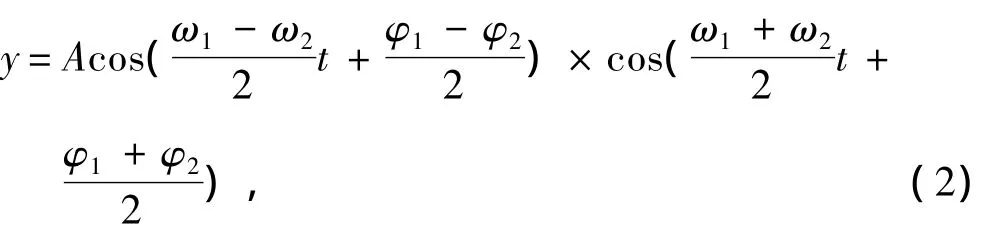
所以激励信号的包络函数为:

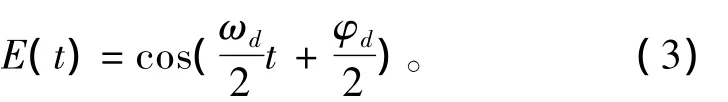
式中:ωd=ω1－ ω2;φd=φ1－ φ2。

根据Moffett暂态参量阵理论［8］可得声轴上的二次差频波声压为:

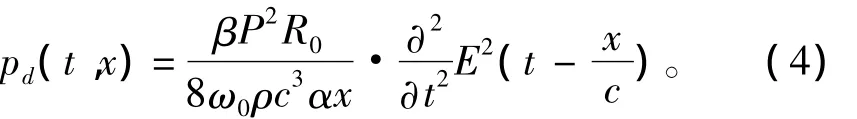
式中:β为介质的非线性系数;P为辐射器表面声压幅值;R0为瑞利距离;ω0为载波的角频率;ρ为介质的密度;c为介质中的声速;α为介质对载波的吸收系数;x为声轴上声信号接收点距离发射阵的距离。

将式(3)代入式(4)得:

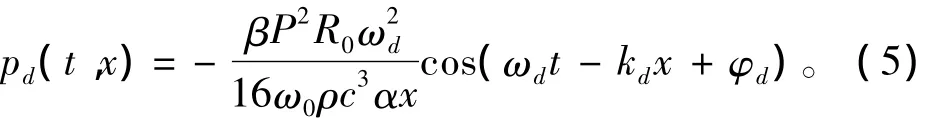
式中kd=ωd/c。

由式(5)可看出，当x一定时，通过改变激励信号的初相位φ1和φ2可以改变差频波的初相位φd，即:

其中φ1为频率较高信号的初相位，式(6)即为参量阵声轴上差频波与原频波的相位关系。

由式(5)还可得出声轴上的差频波幅值为:

所以声轴上距声源x0处差频波与原频波的声压幅值比为:

代入式(8)得:

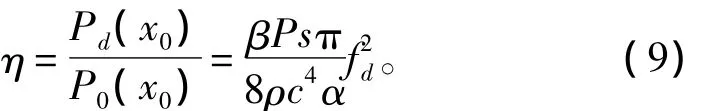
式中s为参量发射阵端面面积。式(9)就是参量阵声轴上差频波与原频波声压比和差频波频率的关系。

2 实验

实验在哈尔滨工程大学水声工程学院水声信道水池中进行。水池长28 m，宽2.5 m，水深2 m，侧壁贴敷吸声橡胶。实验布置和仪器连接框图如图1所示。发射阵和接收水听器置于水池中线水深1 m处，且二者距离可调。

图2所示为自制6×30元六路矩形发射阵。阵长385 mm，宽70.5 mm，阵元间距为5 mm。实验时，六路并联作为一个发射通道，六路并联的发射响应曲线如图3所示。实验中使用的自制低通滤波器的幅频特性曲线如图4所示。

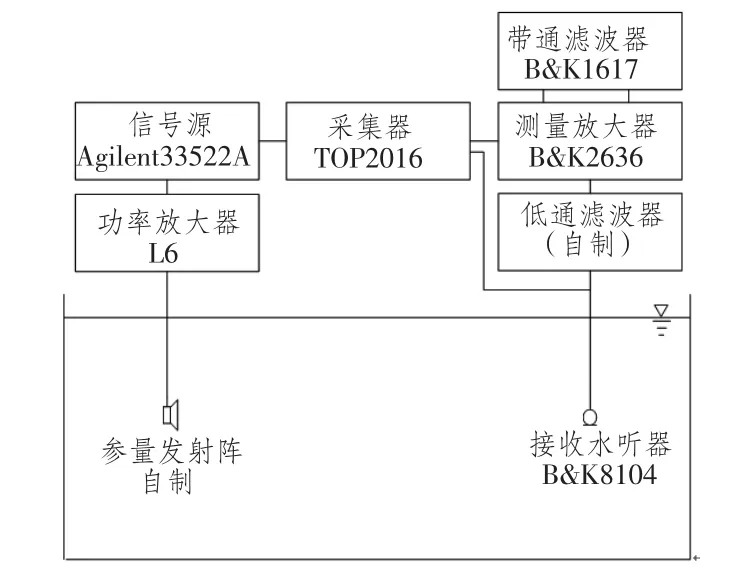
图1 实验布置示意图Fig.1 Schematic diagram of experimental setup

图2 参量阵照片Fig.2 Parametric array picture

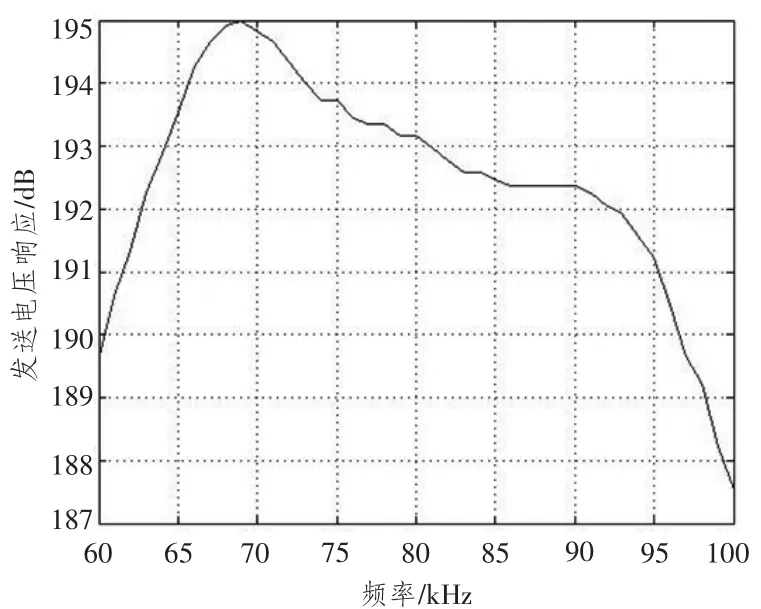
图3 参量阵发射响应Fig.3 Response curve of parametric array

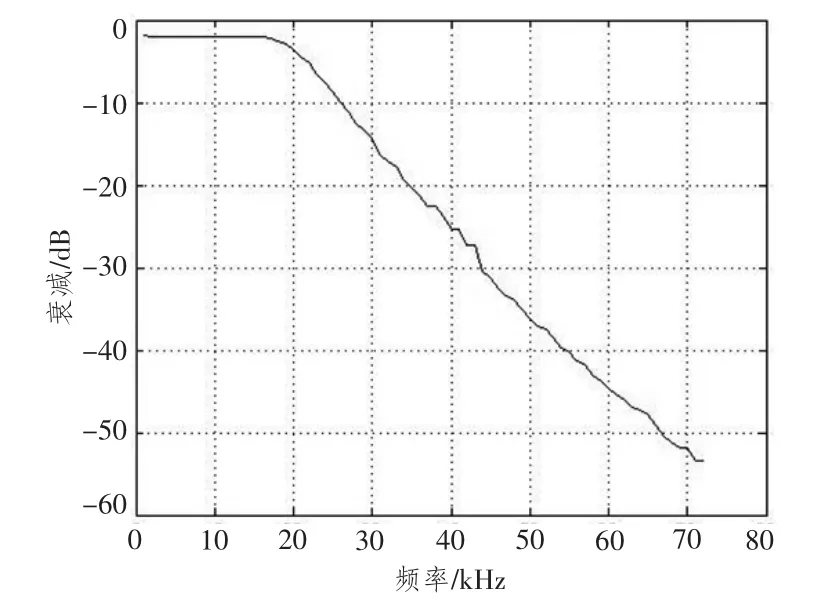
图4 低通滤波器幅频特性Fig.4 Low pass filter amplitude-frequency characterstic

3.1 差频波与原频波相位关系实验

发射阵与水听器距离为2 m。为更好地证明理论的准确性，实验使用2种原频波激励信号进行研究。

首先使用的原频波激励信号为2个幅度相等、频率分别为80 kHz和90 kHz的正弦信号相加，再通过方波脉冲调制得到载频85 kHz调制频率10 kHz的CW脉冲，脉冲宽度为1 ms，脉冲周期为50 ms。该信号的初始相位差通过保持90 kHz信号的初相位 (理论中的φ1)不变，改变80 kHz信号的初相位 (理论中的φ2)来获得。测量放大器的放大量为80 dB，带通滤波器的中心频率为10 kHz。利用信号采集器同时对原频声波信号和差频声波信号进行多次采集。得到原频波和差频波如图5和图6所示。图中所给的信号波形是水听器接收的原频波和差频波脉冲的完整信号。

实验中发射换能器与接收器位置未变，采集器的初始时刻由无延迟的同步触发信号触发，因而，图5和图6的时间零时刻对齐。比较图5和图6可以看出，随原波激励信号中φ2的变化，差频波信号的相位也在变化。比较各图在t=2.2 ms处相位的差别可知，差频波信号的相位有明显变化且变化值与理论值近似相同。

为定量说明差频波相位的变化量，将每次采集到的差频波进行傅里叶变换，通过相位谱找到频率为10 kHz的相位值，并将得到的各差频波的相位值以φ2=0时的相位值为基准，分别与其作差，得到φ2为不同角度时差频波的相位变化量。表1中给出了5组差频波信号的处理结果。

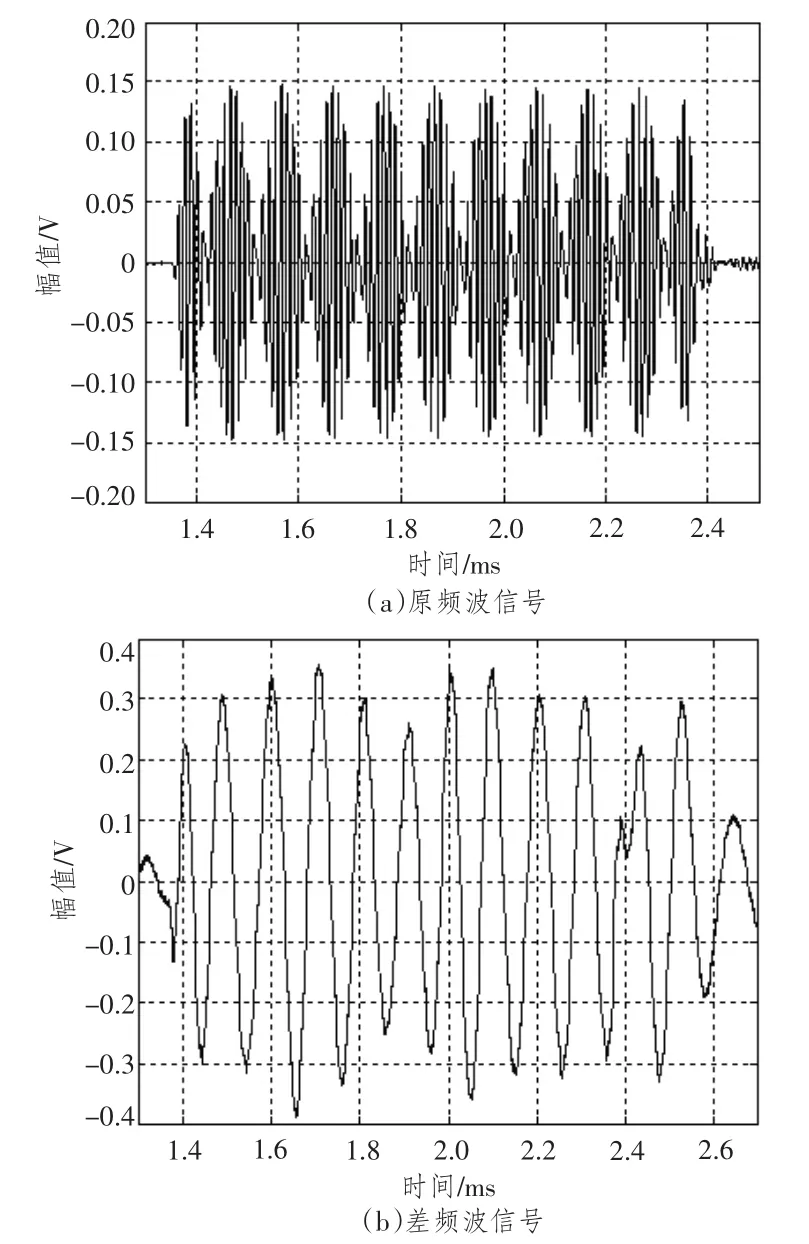
图5 φ2=0时水听器接收的原频波信号和差频波信号Fig.5 The receiving difference and primary CWsignal whenφ2=0

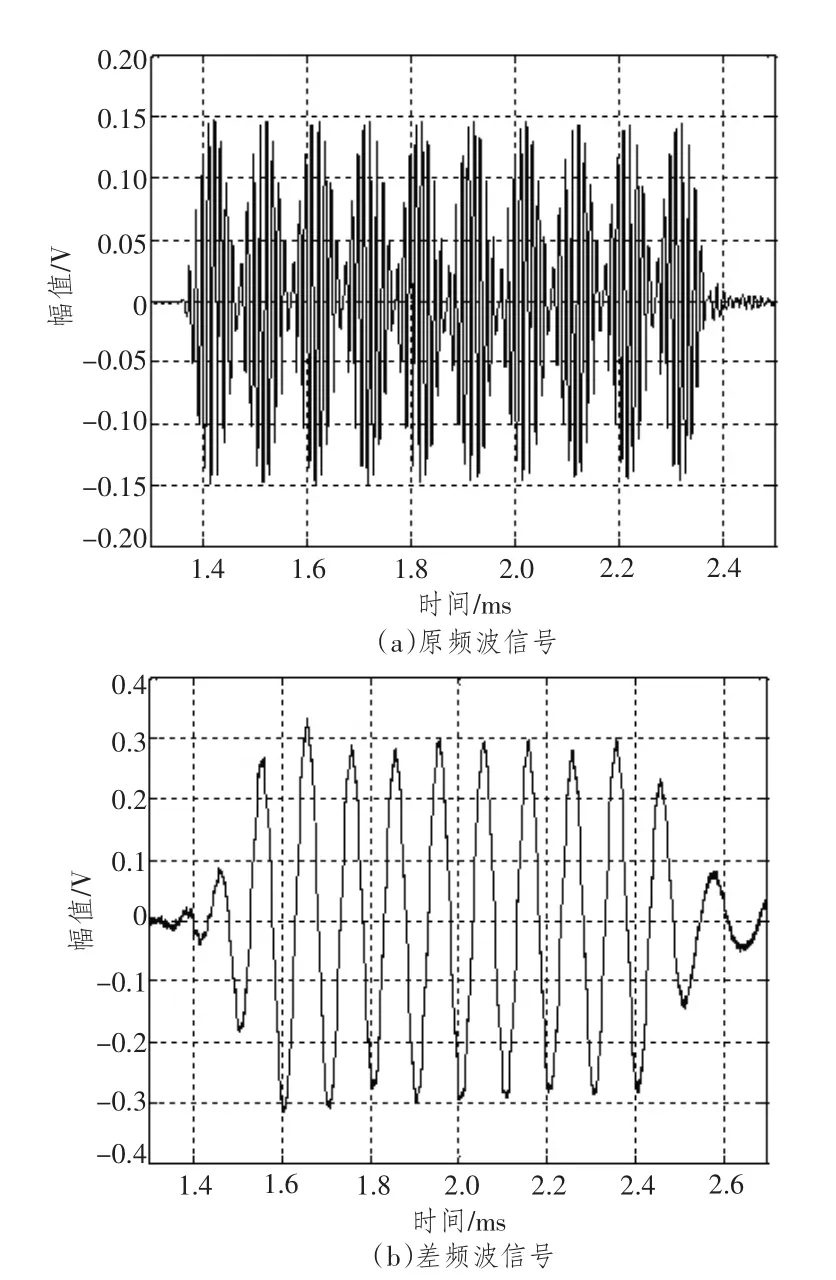
图6 φ2=π时水听器接收的原频波信号和差频波信号Fig.6 The receiving difference and primary CWsignal whenφ2=π

保持其他实验条件不变，将原频波激励信号改为80 kHz和90 kHz的等幅简谐信号相加后再用高斯函数相乘，得到的载频85 kHz调制频率10 kHz的高斯函数脉冲，脉冲宽度为1 ms，脉冲周期为50 ms，信号的初始相位通过保持90 kHz信号的初相位 (理论中的φ1)不变，改变80 kHz信号的初相位 (理论中的φ2)来获得的。使用该信号进行上述相同的实验，并对实验结果采取同样的处理方法，得到结果如图7、图8和表2所示。

本实验结果表明，改变原频波的初相位可以控制差频波的相位，验证了理论的正确性。

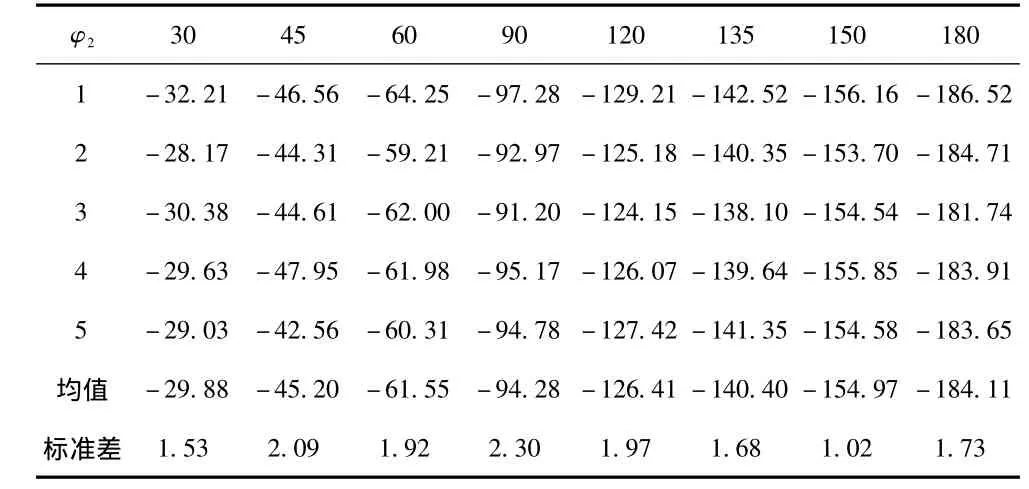
表1 激励信号为CW脉冲信号时差频波的相位变化 (单位/(°))Tab.1 Phase changes of difference frequency wave when excitation signal is CW signal

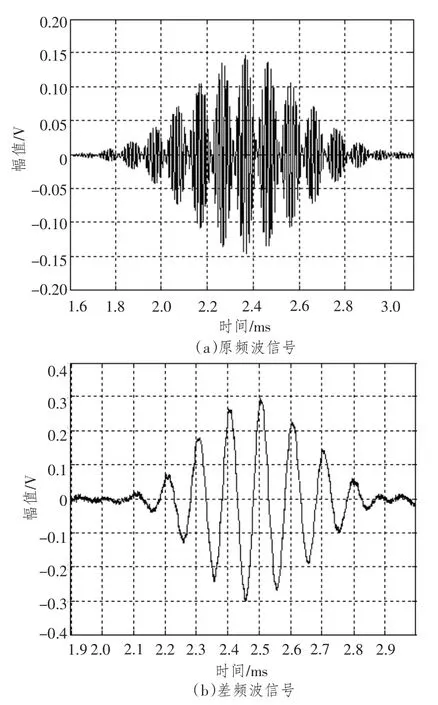
图7 φ2=0时水听器接收的原频波信号和差频波信号Fig.7 The receiving difference and primary Gaussian pulse signal whenφ2=0

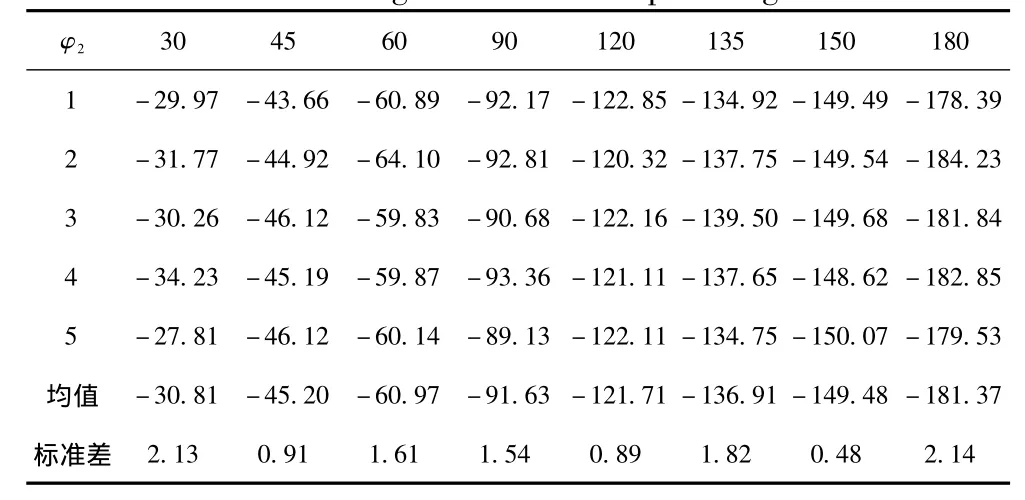
表2 激励信号为高斯脉冲信号时差频波的相位变化 (单位/(°))Tab.2 Phase changes of difference frequency wave when excitation signal is Gaussian pulse signal

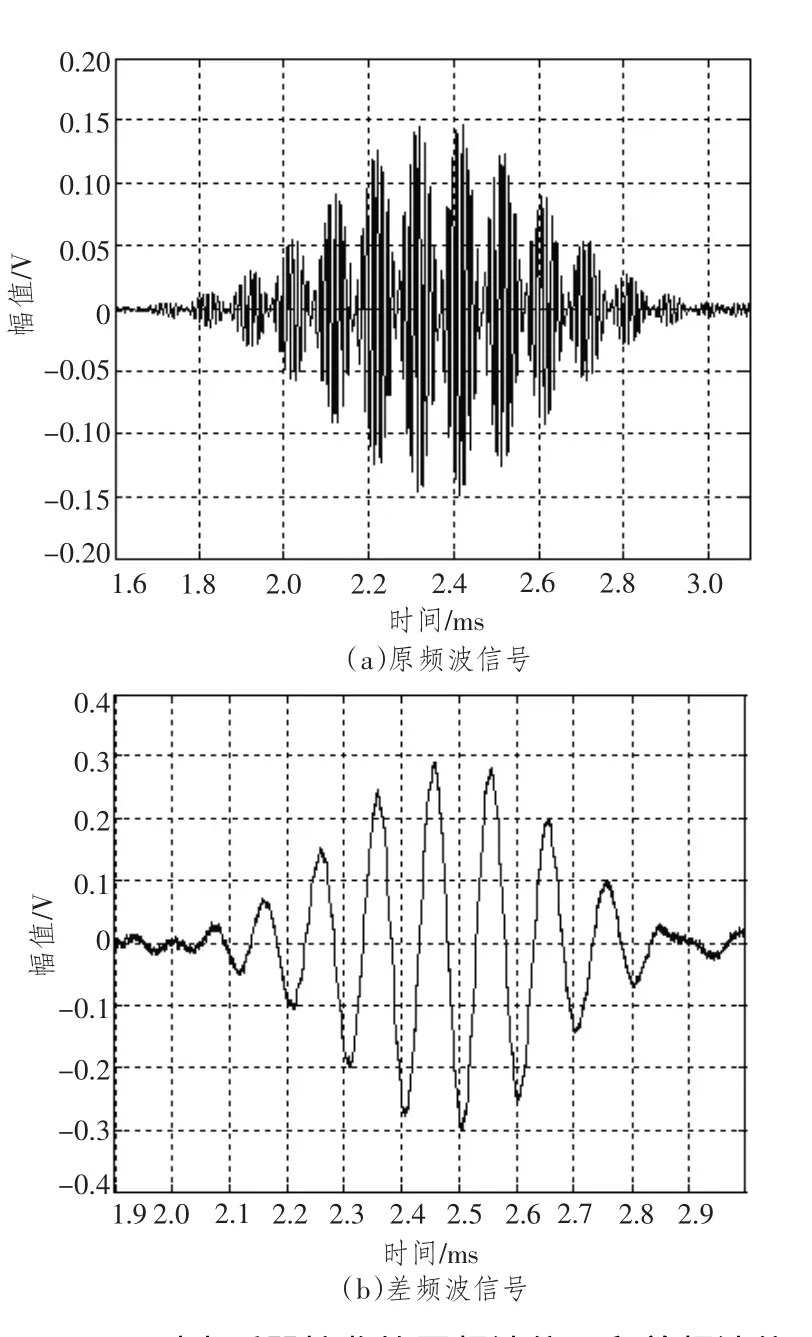
图8 φ2=π时水听器接收的原频波信号和差频波信号Fig.8 The receiving difference and primary Gaussian pulse signal whenφ2=π

2.2 差频波原频波声压幅值比与差频波频率关系仿真与实验

为与后续实验数据进行对比，仿真计算选取的参数为:介质非线性参量β=3.5，表面声压幅值P=1 995 Pa，参量发射阵端面面积s=0.027 m2，介质密度ρ=1 000 kg/m3，介质中声速为c=1 500 m/s，载波频率为f0=85 kHz，介质对载波的吸收系数α=0.000 58 Np/m，声轴上信号接收点距离发射阵的距离x0=10 m。差频波频率fd∈ ［1，10］kHz，最终得到仿真结果如图9所示。图中的理论曲线即为仿真得到的结果。

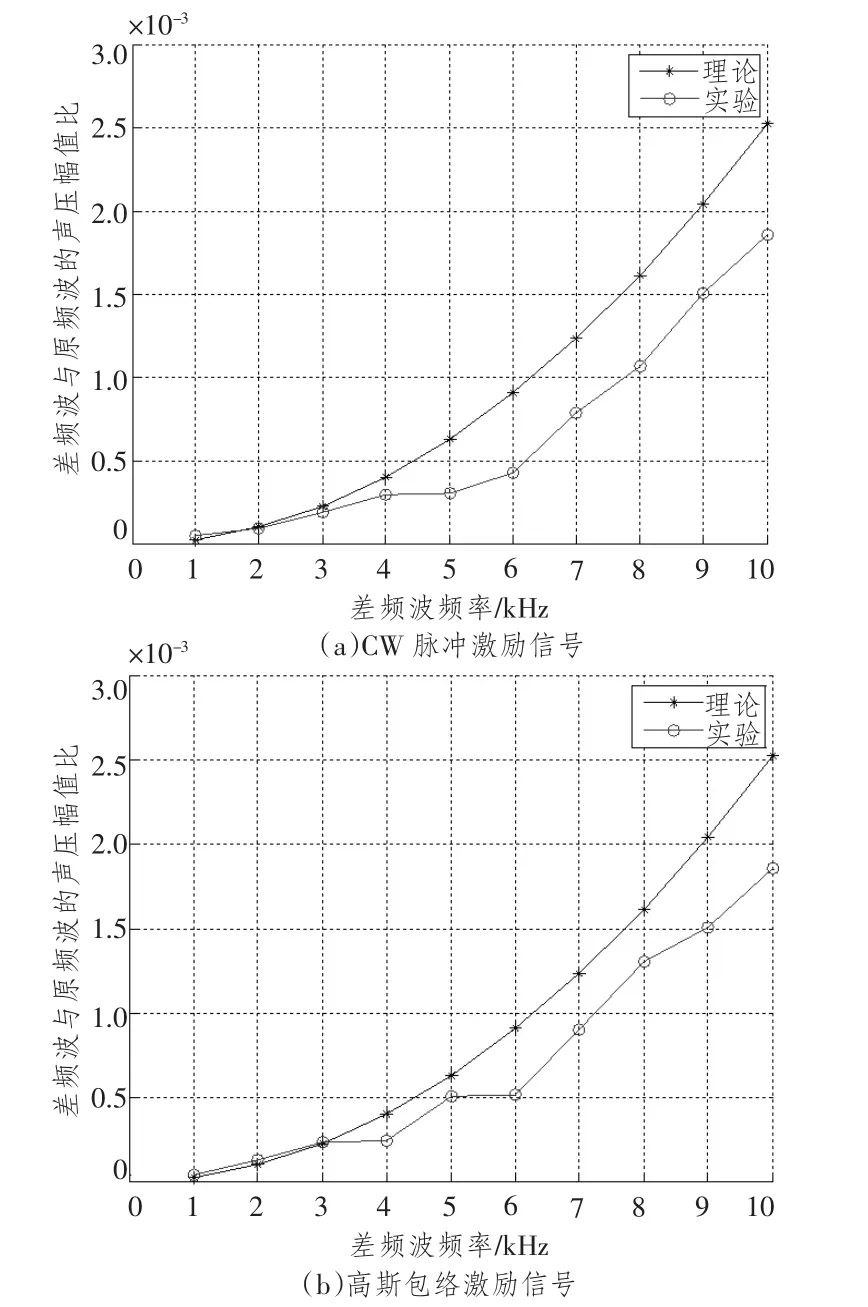
图9 差频波原频波声压幅值比与差频波频率的关系Fig.9 The relationship between the sound pressure ratio of difference frequency and primary signal and the frequency of difference frequency wave

实验布置和仪器连接框图如图1所示。发射阵与水听器距离为10 m。测量放大器的放大量为80 dB。实验用2组信号激励参量发射阵，第1组是载波频率为85 kHz、调制频率为1～10 kHz的方波脉冲信号;第2组是载波频率为85 kHz、调制频率为1～10 kHz的高斯脉冲信号。2组信号的脉冲宽度均为1 ms。信号源、示波器、信号采集器采用同步外触发，触发信号为脉冲周期为100 ms的脉冲信号。

实验中要求接收到的原频波幅值不变，利用信号采集器分别对每个激励信号激励换能器时产生的原频波和差频波进行采集。

对实验数据进行处理，得到两组原频声信号表面声压幅值均为1 995 Pa。考虑水听器接收灵敏度和低通滤波器对信号的影响，忽略带通滤波器在通带内对信号幅值的衰减作用，最终得到不同频率时声轴方向距声源10 m处差频波和原频波的声压幅值比。将实验结果与理论值进行比较，结果如图9所示。由图9可知，实验结果略小于理论值，原因可能是实验时未实现参量阵远场测量。

3 结语

本文对参量发射阵声轴上的差频波与原频波的相位关系以及差频波原频波声压幅值比与差频波频率的关系做了理论和实验研究。由实验结果可以看出，理论与实验规律一致，证明了理论的正确性，为控制差频波相位奠定了理论基础，可以作为参量阵应用研究的参考。

［1］ 何祚镛，赵玉芳．声学理论基础［M］．北京:国防科技出版社，1987．HE Zuo-yong，ZHAO Yu-fang．Theoretical foundation of acoustics［M］．Beijing:National Defense Industry Publishing House，1987．

［2］ 李颂文．参量阵及其在水声工程中的应用进展［J］．声学技术，2011，30(1):9 －16．LI Song-wen．Parametric array and its application in underwater acoustic engineering:an overview［J］．Technical Acoustics，2011，30(1):9 －16．

［3］ TRUCCO A，PESCETTO A．Acoustic detection of objects buried in the sea floor［J］．Electronics Letters，2000，36(5):1595－1595．

［4］ ZAKHARIA M E，POLLET C，REGAUD E．Combined parametric synthetic and interfrometic sonar for the detection of buried objects［C］．IEEE Proceedings of Oceans Europe，2005:522 －526．

［5］ FIORAVANTI S，MAGUER A，LOVIK A．A synthetic aperture parametric sonar for buried object detection［J］．J．Acoust．Soc．Am．1996，100(4):2636．

［6］ WESTERVELT P J．Parametric acoustic array［J］．J．Ac －oust．Soc．Am，1963，35(4):535 －537．

［7］ MOFFETT M B，MELLEN R H．Modle for parametric acoustic sources［J］．J．Acoust．Soc．Am，1977，61(2):325－337．

［8］ MOFFETT M B，MELLEN RH．Parametric acoustic sources of transient signals［J］．J．Acoust．Soc．Am，1979，66(4):1182－1187．