基于主分量的耦合声源数量判别方法研究

李震宇

(大连测控技术研究所，辽宁大连116013)

0 引言

声源的数量及空间位置判别在噪声控制工程中是一个基础问题，在过去已经被广泛研究，提出了一些方法。虽然近场声全息最主要的功能不是用来声源的数量及位置判别，但它可以在实际声场中发现声源的位置。然而，近场声全息仅仅满足具有简单排列结构的声源位置识别，否则可以结合边界元法来识别复杂结构的声源位置判别。此外，近场声全息对于测量条件要求较为严格，必须距离目标较近约为1.5倍波长，使得实际应用较为困难。例如，测量传感器必须非常接近声源才能正确满足其近场条件，如果不知道声源的位置，就无法确定测量位置是否接近声源1.5倍波长。

如果只是想知道声源数量，而不需要确定其空间位置，对于不相干声源是可以实现的。其最有效的方法是通过正交功率谱矩阵分解，不相干源的个数等于矩阵的维数，这一方法称之为正交功率谱矩阵分析法 (CSM)。而声源的空间定位难度比数量识别大的多。1986年，R.O.Schmidt提出一种多种信号分类的方法优越于普通的方法，简称MUSIC算法。然而，该方法最大的缺陷在于:1)源必须是不相干的;2)所有测量通道的信号自谱特征一致。

从信息处理的角度来看，可以通过数学变换将信息描述为由一系列彼此相互独立信号的线性组合，并且这一组信号能够反映原信息的频谱特征与波形特征等，本文在此基础上，结合窄带带通滤波器、功率谱分析，综合分析耦合声源的数量判别，通过理论仿真和建模仿真验证了该方法的可行性和准确性［1－2］。

1 理论分析

对于n个非独立的振动输入信号，利用主分量分析方法进行一定的线性变换，将其转化为p个独立信号和n－p个零信号，从而可以用较少的新变量代替原来的变量，而且能使较少的新变量尽可能多地保留原变量反映的信息，且新变量之间又彼此独立，这种方法非常适合舰船耦合条件下辐射声源数量的识别。

1.1 算法原理

假定有n个振动信息样本，每个样本共有p个变量，构成一个n×p阶的输入信息矩阵:

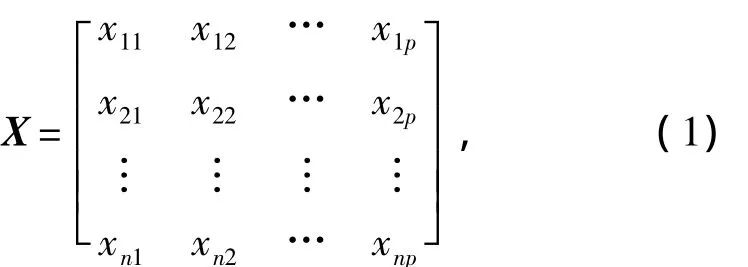
当p较大时，在p维空间中考察问题比较宽泛，需要对输入矩阵进行降维。

设z1，z2，…，zm(m≤p)为新变量指标，则有新变量

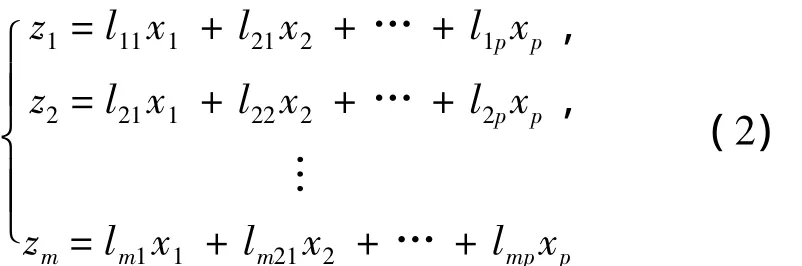
式中:z1为x1，x2，…，xp的一切线性组合中方差最大变量;z2为与z1不相关的x1，x2，…，xp的所有线性组合中方差最大变量;zm为与 z1，z2，…，zm－1都不相关的x1，x2，…，xp的所有线性组合中方差最大变量。新变量指标 z1，z2，…，zm分别称为原变量指标 x1，x2，…，xp的第一，第二，…，第m主分量［3－4］。

主分量分析的实质是确定原变量xj(j=1，2，…，p)在诸主分量 zi(i=1，2，…，m)上的荷载 lij。

1.2 主分量计算方法

1)相关系数矩阵计算

式中 rij(i，j=1，2，…，p)为原变量 xi与 xj的相关系数，rij=rji，其计算公式为:

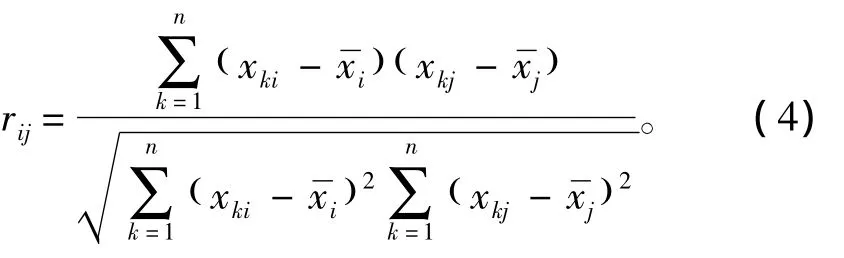
2)特征值与特征向量计算

分解求出特征值，并使其按大小顺序排列λ1≥λ2≥ … ≥ λp≥0。

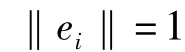
3)主分量荷载计算

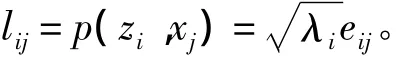
具体流程如图1所示。

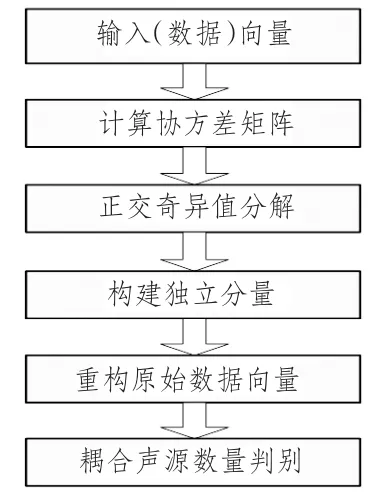
图1 声源数量判别流程图Fig.1 Flow chart of discrimination number on noise source

2 理论仿真研究

假设振动源信号与干扰噪声通过传递到达测量点，从而获得测量输入，如图2所示。源信号为幅值A1和A3的50 Hz正弦信号，以及幅值A2的100 Hz正弦信号，相位是随机的，n1(t)，n2(t)和n3(t)为高斯白噪声，x1(t)，x2(t)和x3(t)为测量输入。

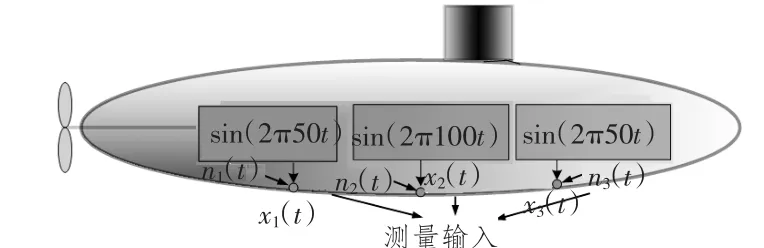
图2 测量模型Fig.2 Measurement model

1)不同信噪比条件下的分析结果

A1，A2和A3初始值均为1，通过增大n3(t)数值改变测量输入x3(t)的信噪比，具体分析结果如表1所示。

表1 信噪比为10 dB和6 dB下的分析结果Tab.1 Analysis results in 10 dB and 6 dB

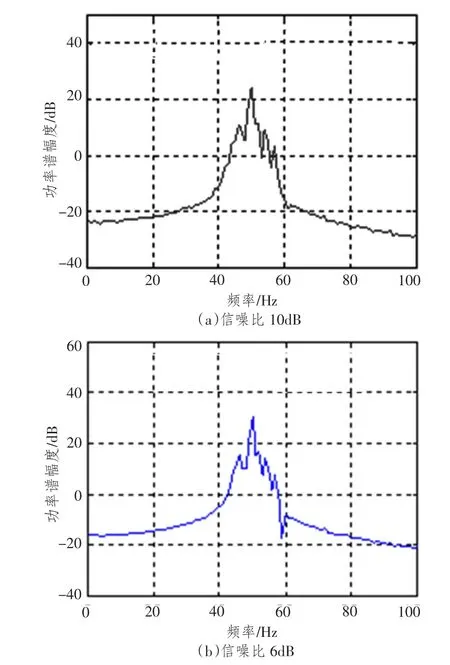
图3 主分量谱图Fig.3 Figure of principal component spectrum

信噪比为10 dB和6 dB时，第一特征根对应的特征向量中存在2个最大值，结合主分量谱图可知对应线谱为50 Hz，表明辐射声场中50 Hz特征频谱的声源数量为2。

表2 信噪比为3 dB和0 dB下的分析结果Tab.2 Analysis results in 3 dB and 0 dB

图4 主分量谱图Fig.4 Figure of principal component spectrum

表2给出了信噪比为3 dB和0 dB时的分析结果。由表可见，在信噪比为3 dB条件下，第一特征根对应的特征向量仍存在2个最大值，结合主分量谱图可知，辐射声场中50 Hz特征频谱的声源数量为2;而信噪比0 dB条件下，第一特征根对应的特征向量存在一个最大值，2个相接近的较大值，说明声源数量为3，这与仿真条件相去甚远，说明在这一信噪比条件下该分析方法无法给出确分析结果。

2)不同信号强度下的分析结果

A1，A2和A3初始值均为1，A1和A2保持不变，通过增大A3数值改变信号x1(t)和x3(t)的幅值比，研究信号强度对分析结果的影响，具体分析结果表3所示。

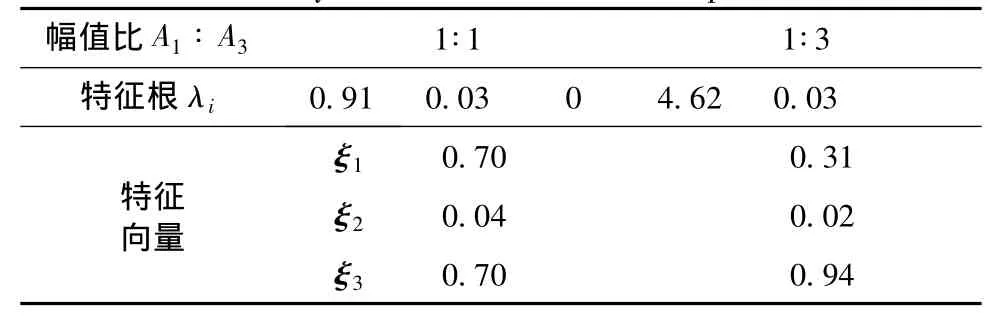
表3 不同幅值比的分析结果Tab.3 Analysis results of different amplitude ratio

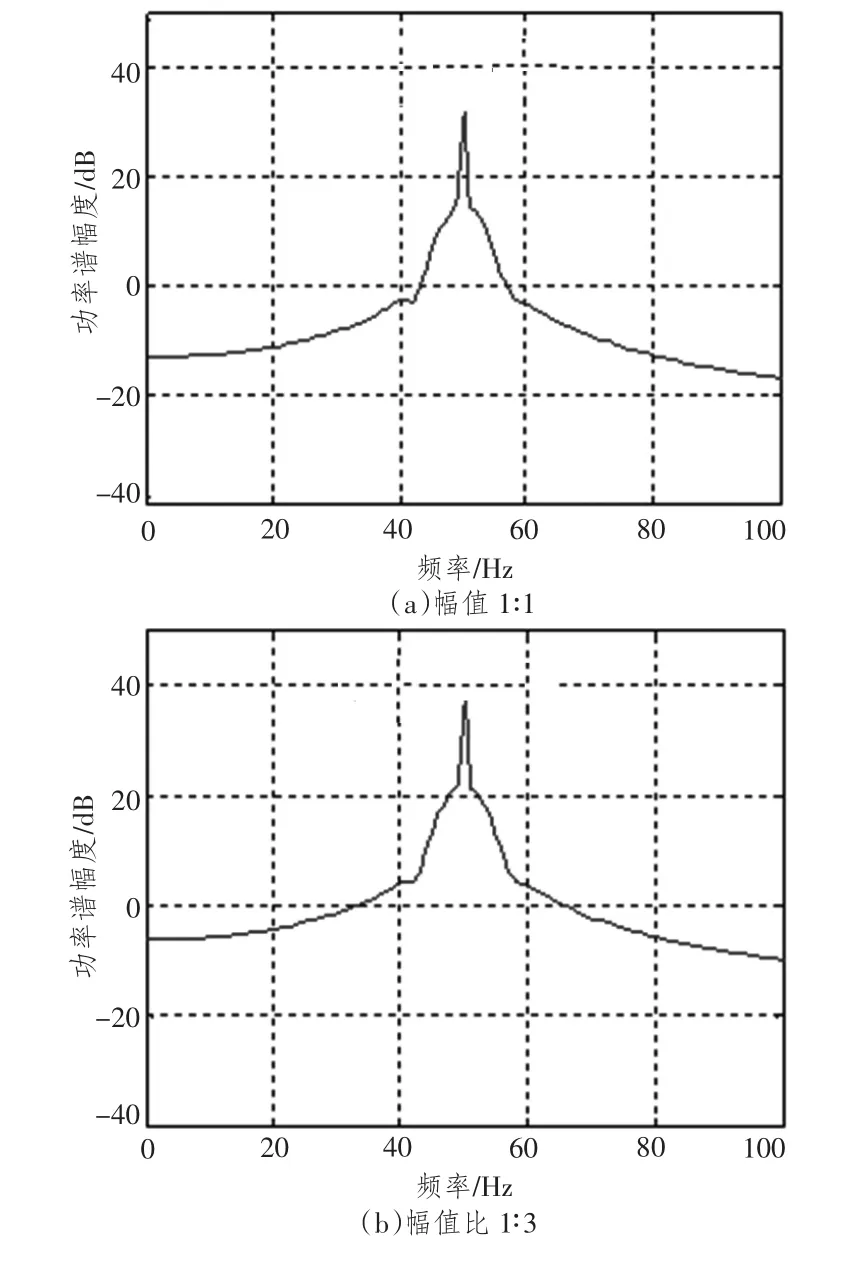
图5 主分量谱图Fig.5 Figure of principal component spectrum

表3给出了幅值比1∶1和1∶3条件下的分析结果，由表可见，通过对比特征系数可见，第一特征根对应的特征向量均存在2个较大值，结合主分量谱图可知，辐射声场中50 Hz特征频谱的声源数量为2。

同理，给出幅值比为1∶4～1∶14条件下的耦合声源数量识别结果，依据结果大小绘制特征系数值随幅值比变化曲线，如图6所示。

由图6可见，随着x3(t)幅值A3的增大，特征系数ξ3增大，ξ1减小，当达到1∶4时，ξ3接近1，ξ1趋近0.2，继续增大，则ξ3无限趋近1，ξ1趋近0，这表明，幅值比1∶4可以认为是主分量识别耦合声源数量的极限，即耦合声源之间的幅值比超过1∶4时，该方法无法得到准确的判别结果。

图6 不同幅值比的分析结果Fig.6 Analysis results of different amplitude ratio

3)相干源数量对分析结果的影响

A1，A2和A3初始值均为1，通过增加与信号x1(t)和x3(t)完全相干源的数量，分析相干源数量对于主分量分析结果的影响，具体分析结果如表4所示。

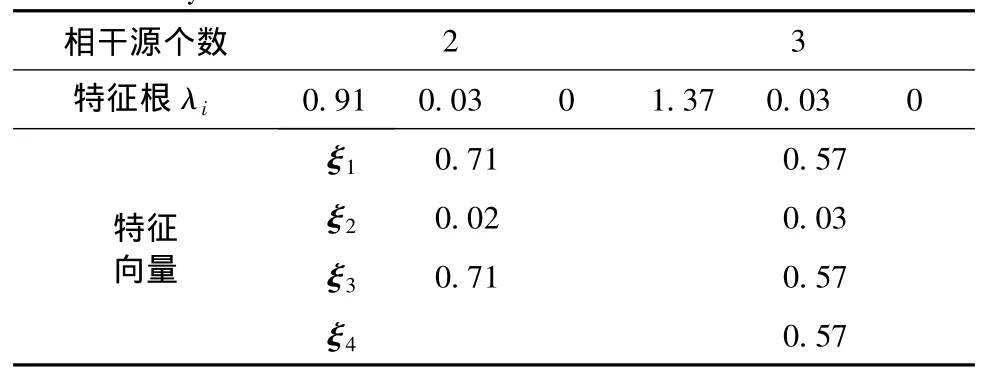
表4 不同相干源个数下的分析结果Tab.4 Analysis results of the number of different coherent sources

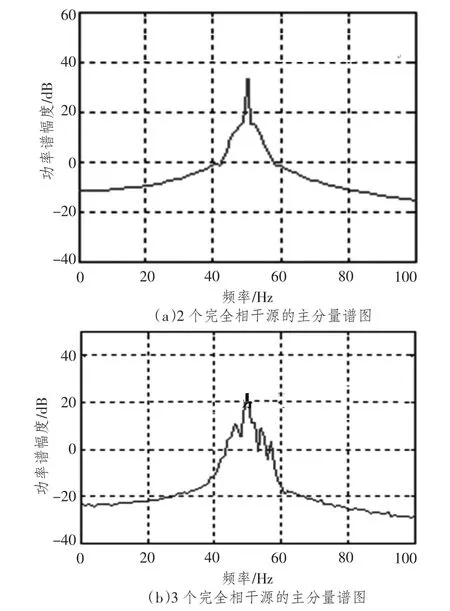
图7 主分量谱图Fig.7 Figure of principal component spectrum

表4给出了存在2个和3个完全相干源的主分量分析结果，由表可见，特征系数分别存在2个和3个最大值，且大小一致，说明同频声源数量分别为2个和3个，与仿真结果一致。

同理，给出4～12个相干源的分析结果，绘制特征系数值随相干源数量增加的变化曲线，如图8所示。由图可见，相干源个数由2个逐渐增加到12个时，对应的特征系数最大值也由2个逐渐增加到12个，表明辐射声场中50 Hz特征频谱的声源数量相对应的由2个逐渐增加到12个;而且，随着相干源个数的增加，使得特征系数值相对大小在逐渐减小，由0.71下降至0.29，说明相干源过多不利于声源数量的识别。

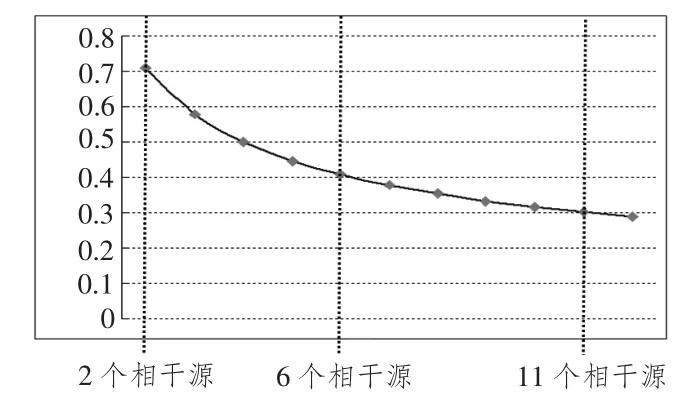
图8 不同相干源数量的分析结果Fig.8 Analysis results of the number of different coherent sources

3 基于理论模型数据的研究

利用Ansys建模软件，建立某型潜艇1∶1模型，在模型内部壳体上施加不同激励源模拟潜艇振动经过壳体向水下辐射噪声的过程，F1，F2和F3分别为施加在壳体上的3个激励力，其中，F1和F3为同频(100 Hz)、初始相位不同的激励源，从而模拟耦合声源激励壳体振动产生声辐射。具体激励位置如图9所示。

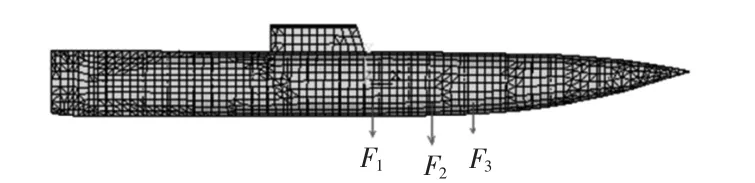
图9 缩比模型激励点位置图Fig.9 Contraction ratio model of the excitation point position

图10给出了辐射噪声功率谱，由图可见，辐射噪声中存在100 Hz和150 Hz特征线谱。下面依据信息模型的仿真计算结果，利用壳体上分布的5个响应测点信息构建主分量分析的输入信息矩阵。下面针对辐射噪声中存在的100 Hz和150 Hz线谱，分别进行声源数量判别。

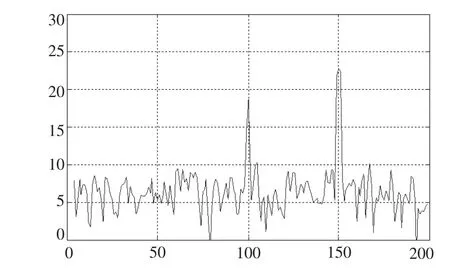
图10 辐射噪声功率谱图Fig.10 Spectrum of radiated noise power

1)100 Hz噪声源数量的判别

信号首先通过100阶FIR带通滤波器，其通带频率为90～110 Hz，然后对输出信号进行主分量分析，分析结果见表5。第一特征根的累计贡献率为99.3%，因此，只需考虑第一特征向量。

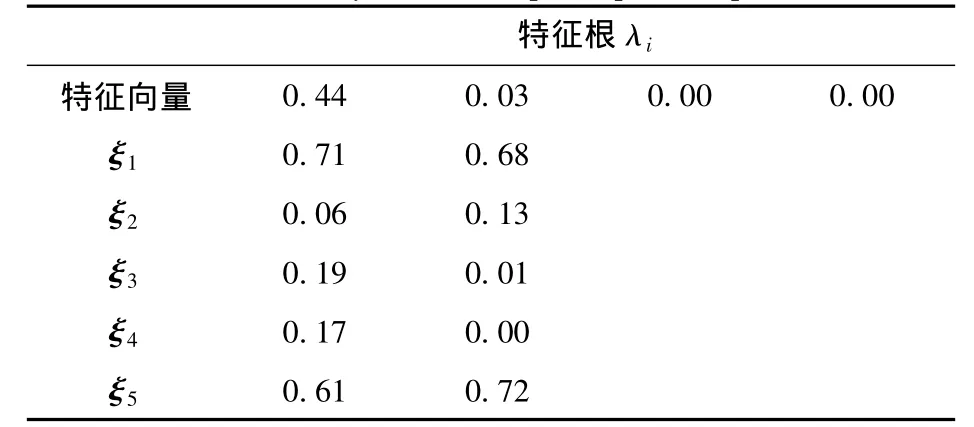
表5 主分量分析结果Tab.5 Analysis results principal component

图11 主分量谱图Fig.11 Figure of principal component spectrum

通过对比特征向量数值的大小，可见，存在2个较大值，结合主分量谱图可知，辐射噪声中的100 Hz线谱主要来源主要有2个。

2)150 Hz噪声源数量的判别

信号首先通过同样的FIR带通滤波器，然后对输出信号进行主分量分析，分析结果见表6。第一特征根的累计贡献率为98.7%，因此，只需考虑第一特征向量。

表6 主分量分析结果Tab.6 Analysis results principal component

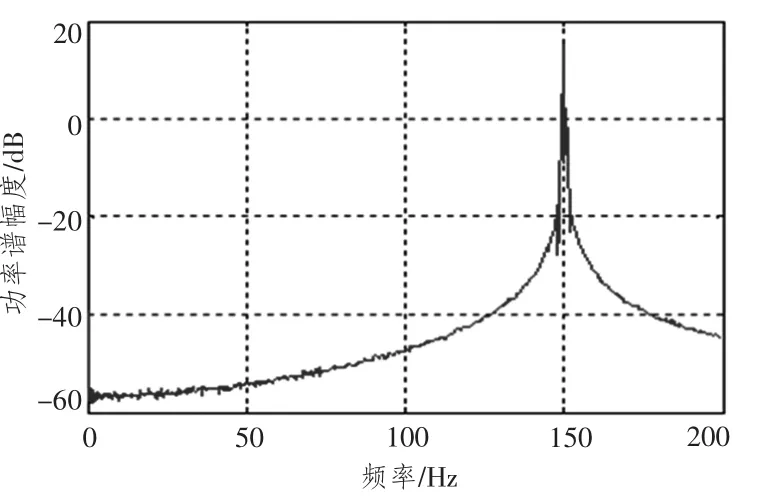
图12 主分量谱图Fig.12 Figure of principal component spectrum

通过对比特征向量数值的大小，可见，存在1个最大值，结合主分量谱图可知，辐射噪声中的150 Hz线谱主要来源有1个。

4 结语

建立了基于主分量分析的耦合源数量判别方法，通过理论仿真和基于信息模型数据的分析研究，表明该方法结合FIR数字滤波器和主分量谱分析可以很好地实现输入信息中独立声源和耦合源数量的判别。

［1］ 王之程，程宗歧，于沨，等．第1版．舰船噪声测量与分析［M］．北京:国防工业出版社，2004(1):1－5．

［2］ 王国强．实用工程数值模拟技术及其在ANSYS上的实践［M］．西安:西北工业大学出版社，1999．

［3］ 马建仓，牛奕龙，陈海洋．盲信号处理(第1版)［M］．北京:国防工业出版社．2006．

［4］ ZHANG Xian-da，ZHU Xiao-long，BAO Zheng．Grading learing for blind source separation［J］．Science in China SeriesF － Information Sciences，2003，46(1):31 －44．

［5］ 李舜酩．机械振动盲源信号识别的时域方法［J］．应用力学学报，2005，22(4)．

［6］ 王凌燕，黄公亮，侯文．基于独立分量分析的潜艇振动信号盲分离技术［J］．计量与测试技术，2009，36(3):14－16．

［7］ 贾金玲，姚毅，陈志利．基于ICA的盲信号分离算法研究［J］．四川理工学院学报(自然科学版)，2007，20(2):72－76．