一种单轴旋转INS大方位失准角下快速对准方法

于化鹏，郭正东,2,3，蔡 鹏，海 深，莫 军

(1.海军潜艇学院，山东 青岛 266042；2.中国科学院海洋研究所，山东 青岛 266071；3.中国科学院大学，北京 100049；4.铜陵学院 数学与计算机学院，安徽 铜陵 244000)

一种单轴旋转INS大方位失准角下快速对准方法

于化鹏1，郭正东1,2,3，蔡 鹏1，海 深4，莫 军1

(1.海军潜艇学院，山东 青岛 266042；2.中国科学院海洋研究所，山东 青岛 266071；3.中国科学院大学，北京 100049；4.铜陵学院 数学与计算机学院，安徽 铜陵 244000)

以单轴连续旋转式惯导系统为研究对象，针对惯导系统误差模型的非线性本质和对初始对准快速性的要求，通过推导其静基座条件下大方位失准角误差方程，设计一种利用超球体单形采样的UKF滤波器，并通过实际测试验证其有效性。实验结果表明，利用所设计的UKF滤波算法，10 min方位角对准精度能够达到优于0.008°。

大失准角；初始对准；无迹卡尔曼滤波；旋转

0 引 言

由于其简洁性、鲁棒性、高可维护性等自身特有的优势，捷联惯导系统(SINS)近几十年来得到快速发展，并已广泛应用于航空航天、航海、陆地导航等领域[1-2]。得益于自动控制技术和电子技术的飞速发展，通过计算机能够方便地实现捷联惯导系统的机械编排，使得采用旋转调制方法来补偿惯性测量单元(IMU)惯性器件误差的技术引起世界各国投入大量人力物力进行研究[3-6]。

通过在IMU的外围加上单轴转台并设计规律性的旋转次序，单轴旋转调制方法能够实现不利用外部信息而在一个周期内将部分IMU惯性器件的慢变误差在导航坐标系内投影成周期变化量，进而在导航解算过程中，这些慢变误差的影响将在整个转动周期内积分运算后平均抵消，进而大大减少了惯导系统的误差累积，达到更好发挥其“自主性”、提高系统对准速度和精度的效果[3-8]。单轴旋转调制方法中，连续旋转方案避免了对转台控制系统及其性能指标的严苛要求[7-10]。

初始对准是惯导系统实际应用中的重要环节，衡量对准算法的2项重要技术指标即为精度和快速性。由于军事应用的特殊性，国外对单轴连续旋转式惯导系统(Single-axis Continuously Rotary Inertial Navigation System，SCR-INS)的初始对准与导航算法的公开报道很少[7-10]。在国内的相关研究中，文献[7]利用其连续旋转的特点，采用标准Kalman滤波算法抑制了SCR-INS中系统噪声的影响，且3 min方位对准精度能够达到3.003′(陀螺精度为0.03°/h，1σ)；通过建立IMU惯性器件误差变化的二次多项式拟合模型并进行误差在线整周期拟合估计与补偿，文献[8]设计了适用于SCR-INS快速初始对准的标准卡尔曼滤波算法，在系统完全静止时方位角对准精度达到10min优于30″(1σ)；文献[9]利用SCR-INS中IMU惯性器件误差的周期特性，在考虑初始参数装订误差条件下，为其初始对准过程构造了约束状态卡尔曼滤滤器，方位角对准精度达到10min优于10″(1σ)；文献[10]在分析速度残差序列的基础上，提出了一种适用于SCR-INS晃动基座初始对准的自适应滤波滤波算法，大大提高了SCR-INS的工程实用性。

惯导系统误差模型本质上是非线性的，在达到足够的精对准精度条件下，通过对其进行线性处理后，才可以利用标准卡尔曼滤波算法进行精对准等[11-12]。随着非线性滤波技术的发展，为了提高初始对准的快速性，近年来越来越多的研究成果直接考虑大失准角下初始对准的误差模型及其算法。同时，一般情况下，初始对准中方位角误差收敛较慢，是影响粗对准精度的主要因素[12-13]。

本文结合各种非线性滤波方法的计算效率和工程适用性，开展利用无迹卡尔曼滤波(UnscentedKalmanFilter，UKF)进行SCR-INS的大方位失准角下初始对准研究。当前已发表文献中，大多仅对UKF算法进行仿真研究。本文通过深入分析SCR-INS误差特性，实际测试验证所设计的UKF滤波算法的方位角对准精度。

1 初始对准UKF滤波模型的建立

首先定义本文中将用到的单轴连续旋转式惯导系统实验平台中各坐标系，如图1所示。

图1 SCR-INS中坐标系关系Fig.1 Coordinates in the single-axis continuously rotary inertial navigation system

坐标系定义如下：

g系(OXgYgZg)，IMU传感器安装坐标系；为了给3个陀螺提供一致的旋转调制速率，本文中IMU传感器采用斜置安装结构[3,9-10]，各坐标轴固连在陀螺敏感轴上；理想情况下，g系为正交系；

b系(OXbYbZb)，转台台面载体系；Xb轴和Yb轴固定在转台台面内随台面一起绕旋转轴转动，与Zb轴构成右手直角坐标系；

b0系(OXb0Yb0Zb0)，转台台体系，Xb轴与固连在转台台体上的零位指示器重合时的b系，称之为b0系；

另外，选择地心惯性坐标系为i系，“北-东-地(NED)” 当地地理坐标系为n系。

1.1 滤波模型

假设姿态误差角为φ=[φNφEφD]T，则由坐标变换矩阵得:

(1)

其中n′系为实际计算得到的数学平台。在本文仅有大方位失准角假设条件下，对式(1)进行整理并忽略小量乘积后，有：

(2)

同时，可以得到：

(3)

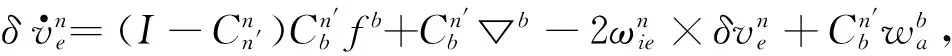
(4)

(5)

(6)

(7)

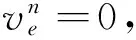
(8)

其中V为观测噪声。

1.2 UKF滤波方案

基于无迹变换思想，UKF采用无迹变换将标准卡尔曼滤波时间更新递推替代且计算量与其基本相当，从而直接应用于非线性误差方程传播系统各误差状态的后验概率分布特性，适用于本文中讨论非线性系统的滤波问题[14]。

考虑到SCR-INS导航解算的实时性要求，需尽量降低计算负载，这就要控制Sigma点的个数。本文UKF滤波器设计中，采用超球体单形采样策略，此时考虑中心点的Sigma点数目为L=m+2(m为系统误差状态变量个数)[15-16]。

利用计算机运行时，需要对式(4)～式(8)所表述的连续系统进行离散化，可记为：

(9)

其中，uk和Vk满足：

(10)

式中δkj为Kroneckerδ函数。

本文所设计的UKF滤波递推算法流程如图2所示[14-16]。

图2 UKF滤波递推算法流程Fig.2 Recursive algorithm process utilizing unscented Kalman filter

2 实验结果及分析

为了验证所设计的UKF滤波算法的有效性及检验利用该算法时初始对准方位角对准精度和误差收敛速度，利用某型SCR-INS进行了实际测试验证。实际测试过程中，为了便于统计分析，将系统置于大致调平的静基座上后，不再改变转台零位指示器的方位，即只进行单位置静基座初始对准实验测试。下面，将详细说明实验及分析结果。

图3所示为某次初始对准测试时10min内方位角收敛曲线。根据图3可见，利用所设计的UKF滤波算法进行初始对准时，方位角开始阶段波动较大，约4min后趋于稳定。综合以上得出结论，所设计的UKF滤波算法是有效的，能够达到使方位角快速收敛的目的。

为了评价该算法的方位角对准精度，可以进行测试得到多次10min对准方位角结果，然后进行统计分析。直观起见，方位角误差结果数据4所示。表1列出了方位角误差数据及分析结果。

图3 某次初始对准10 min内方位角收敛曲线Fig.3 Azimuth convergence curve within 10 minutes during initial alignment

图4 多次测试10 min对准方位角误差统计图Fig.4 Statistical chart of azimuth errors at 10 minutes for multiple initial alignment tests

根据表1中静基座9组实际测试方位角误差统计结果可见，10min对准方位角误差标准差为0.0075°(27.1″)，使得系统初始对准精度能够满足实际应用指标要求。

表1 静基座9组测试10 min对准方位角误差数据Tab.1 Azimuth errors at 10 minutes for 9 tests during stationaryinitial alignment

3 结 语

利用旋转调制方法，惯导系统能够达到较高的对准和导航精度。单轴连续旋转调制方案具有结构简单等不可比拟的优势，对其进行深入研究具有重要的理论意义和工程价值。考虑到惯导系统误差模型的非线性本质以及实际应用中对初始对准快速性的要求越来越高，在推导单轴连续旋转式惯导系统大方位失准角下静基座初始对准误差方程基础上，基于超球体单形采样策略设计了一种UKF初始对准滤波算法。利用某型单轴连续旋转式惯导系统进行实际测试结果表明，所设计的UKF算法是有效性的，能够达到使方位角快速收敛，10min对准方位角精度达到优于0.008°。

[1]GIBSONC，FLUECKIGERK，HOPKINSR，etal.Demons-tratingpracticalinertialnavigation:thebeginningsandbeyond[C]//ProceedingsofAIAAGuidance,Navigation,andControl(GNC)Conference.Boston,MA:AmericanInstituteofAeronauticsandAstronautics,Inc.,August19-22,2013:5122(5121-5112).

[2]BRAUNRD，PUTNAMZR，STEINFELDTBA.Advancesininertialguidancetechnologyforaerospacesystems[C]//ProceedingsofAIAAGuidance,Navigation,andControl(GNC)Conference.Boston,MA:AmericanInstituteofAeronauticsandAstronautics,Inc.,August19-22,2013:5123(5121-5118).

[3]KURYATOVVN，CHEREMISENOVGV，PANASENKOVN,etal.MarineINSBasedontheLaserGyroscopeKM-11[C]//ProceedingsofSymposiumGyroTechnology2002.Stuttgart,Germany:GermanInstituteofNavigation(DGON),September17-18,2002:19.0-19.17.

[4]TUCKERT，LEVINSONE.TheAN/WSN-7BMarineGyrocompass/Navigator[C]//ProceedingsofIONNTM2000.Anaheim,CA:InstituteofNavigation,January26-28, 2000: 348-357.

[5]NIEQ，GAOX，LIUZ.ResearchonaccuracyimprovementofINSwithcontinuousrotation[C]//Proceedingsofthe2009IEEEInternationalConferenceonInformationandAutomation.Zhuhai/Macau,China:InstituteofElectricalandElectronicsEngineers,Inc.,June22-25,2009:870-874.

[6]GELLERES.Inertialsystemplatformrotation[J].IEEETransactionsonAerospaceandElectronicSystems,1968,AES-4(4):557-568.

[7] 张思将.旋转式激光陀螺寻北仪寻北算法研究[D].长沙:国防科技大学,2005:28-38.

ZHANGSi-jiang.Researchonalgorithmoftherotaynorth-finderbasedonringlasergyroscope[D].Changsha:NationalUniversityofDeefnseTechnology,2005:28-38.

[8] 张岩,吴文启,张晓强，等.静基座速率偏频激光陀螺捷联惯导系统快速高精度初始对准算法[J].系统工程与电子技术,2011,33(12):2706-2710.

ZHANGYan,WUWen-qi,ZHANGXiao-qiang,etal.FastandhighaccuracyinitialalignmentalgorithmforratebiasedRLGSINSonstationarybase[J].SystemsEngineeringandElectronics,2011,33(12):2706-2710.

[9]YUH,WUW,HAOM.RapidinitialalignmentundergeographiclatitudeuncertaintyofasinglerotationAHRSonstationarybase[C]//The11thIEEEInternationalConferenceonElectronicMeasurement&Instruments,ICEMI’2013,Harbin,China,August16-18,2013:96-100.

[10] 于化鹏, 吴文启, 曹聚亮, 等.单轴恒速偏频激光陀螺航姿系统晃动基座快速对准自适应滤波方法[J].中国惯性技术学报,2013,21(2):169-173.

YUHua-peng,WUWen-qi,CAOJu-liang,etal.Adaptivefilteringalgorithmtorapidalignmentforsingle-axisconstantratebiasedRLGAHRSonrockingbase[J].JournalofChineseInertialTechnology,2013,21(2):169-173.

[11] 赵红宇, 王哲龙, 姜鸣, 等.基于EPEA的SINS大失准角非线性初始对准方法[J].大连理工大学学报,2012,52(5):736-742.

ZHAOHong-yu,WANGZhe-long,JIANGMing,etal.SINSnonlinearinitialalignmentmethodsforlargemisalignmentanglesbasedonEPEA[J].JournalofDalianUniversityofTechnology,2012,52(5):736-742.

[12]FANGJ,YANGS.StudyoninnovationadaptiveEKFforin-flightalignmentofairbornePOS[J].IEEETransactionsonInstrumentationandMeasurement,2011,60(4):1378-1388.

[13] 郝燕玲, 杨峻巍, 陈亮, 等.基于平方根中心差分卡尔曼滤波的大方位失准角初始对准[J].中国惯性技术学报,2011,19(2):180-187.

HAOYan-ling,YANGJun-wei,CHENLiang,etal.Initialalignmentoflargeazimuthmisalignmentbasedonsquarerootcentraldifferencekalmanfilter[J].JournalofChineseInertialTechnology,2011,19(2):180-187.

[14] 周卫东, 乔相伟, 吉宇人, 等.基于新息和残差的自适应UKF算法[J].宇航学报,2010,31(7):1798-1804.

ZHOUWei-dong,QIAOXiang-wei,JIYu-ren,etal.Aninnovationandresidual-basedadaptiveUKFalgorithm[J].JournalofAstronautics,2010,31(7):1798-1804.

[15] 朱联祥, 况卢娟.基于超球体单形采样的BS-UKF算法在单站无源目标跟踪中的应用[J].重庆邮电大学学报(自然科学版),2010,22(3):299-301,319.

ZHULian-xiang,KUANGLu-juan.Applicationofsphericalsimplexsamplingbasedbackward-smoothingUKFtosingleobserverpassivetracking[J].JournalofChongqingUniversityofPostsandTelecommunications(NaturalScienceEdition),2010,22(3):299-301,319.

[16] 胡宇, 张世英, 杨月诚, 等.基于超球体平方根无迹Kalman滤波算法的涡扇发动机气路部件故障诊断[J].航空动力学报,2014,29(3):689-695.

HUYu,ZHANGShi-ying,YANGYue-cheng,etal.Faultdiagnosisofgaspathcomponentsofturbofanenginebasedonsphericalsquarerootunscentedkalmanfilteralgorithm[J].JournalofAerospacePower,2014,29(3):689-695.

Rapid initial alignment of large azimuth misalignment angle for single-axis rotary INS

YU Hua-peng1, GUO Zheng-dong1,2,3, CAI Peng1, HAI Shen4, MO Jun1

(1.Navy Submarine Academy,Qingdao 266042,China;2.Institute of Oceanology, Chinese Academy of Sciences,Qingdao 266071,China;3.University of Chinese Academy of Sciences,Beijing 100049,China；4.Department of Mathematics and Computer, Tongling College,Tongling 244000,China)

The single-axis rotary inertial navigation system (INS) is studied.Regarding the nonlinearity nature of the INS error dynamic model and the requirement of initial alignment rapidity, an unscented Kalman filter with spherical simplex sampling is designed by deriving the large azimuth misalignment angle error equations of the single-axis rotary strapdown INS on stationary base.Then, tests are done on a postulate system to verify the effectiveness of the UKF approach.The experimental results show that, by using the designed UKF approach, azimuth angle precision within 10 minutes has achieved to be less than 0.008°.

large misalignment angle; initial alignment; unscented kalman filter; rotary

2015-03-11；

2015-04-01

国家高技术研究发展计划(863计划)资助项目

于化鹏(1985-)，男，博士，助教，主要从事高精度导航系统研究。

U666.1

A

1672-7649(2015)10-0100-05

10.3404/j.issn.1672-7649.2015.10.021