一种多工况的滚动轴承损伤状态识别方法

周涛涛，朱显明，刘 彦，彭伟才

(1.中国舰船研究设计中心，湖北 武汉 430064; 2.船舶振动噪声重点实验室，湖北 武汉 430064)

一种多工况的滚动轴承损伤状态识别方法

周涛涛1,2，朱显明1,2，刘 彦1,2，彭伟才1,2

(1.中国舰船研究设计中心，湖北 武汉 430064; 2.船舶振动噪声重点实验室，湖北 武汉 430064)

针对多工况条件下的滚动轴承损伤状态识别问题，本文提出基于CEEMD能量熵和阶次跟踪的损伤识别方法。将振动信号经CEEMD分解为系列的IMF分量，选取其中包含滚动轴承特征频率的IMF分量，运用改进的希尔伯特变换求得IMF分量的边际谱，并利用阶次跟踪方法消除不同转速对损伤状态的影响，同时采用能量熵加强对各损伤状态的识别能力。最后使用特征阶次幅值和能量熵构建诊断特征向量，采用遗传算法优化的支持向量机对损伤状态进行识别。试验结果表明，基于能量熵和阶次跟踪的损伤识别方法精度较高，是一种有前途并且非常有效的多工况损伤状态识别方法。

损伤识别；阶次跟踪；CEEMD能量熵；支持向量机

0 引 言

旋转机械中滚动轴承是必不可少的部件，其中将近1/3的故障由滚动轴承引发。因此，以滚动轴承为研究对象，开展相应的故障损伤分析具有重要的工程价值。文献[1]的研究表明，滚动轴承的振动信号与轴承损伤的类型、程度、部位及其原因等密切相关，目前利用振动信号的故障损伤监测方法应用广泛。

近年来，针对滚动轴承的损伤状态评估，学者们开展了大量的研究。Batista等[2]分析了轴承故障诊断中的特征参数和模式识别方法。轴承故障的特征信息提取主要包括时域分析和频域谱分析方法[3-4]。另外，包络分析和解调技术在轴承故障诊断方面也有应用[5]。鉴于滚动轴承出现损伤故障时振动信号大多表现为不平稳信号，一些时频分析方法如小波分析、经验模态分解以及局域均值分解[6-8]等被用来分析这些复杂的振动信号。

目前大多数的旋转机械状态识别研究成果局限于稳定旋转速度的工况条件。但通常情况下，机械旋转系统由于不同的工况条件，会在不同的旋转速度下工作。在变速度的工况条件下，旋转机械故障的特征参数如特征频率会随着旋转速度的变化而改变。根据Loughlin和Tacer[9]的研究，瞬时频率和阶次跟踪技术能够获取状态管理的有用信息。Fyfe和Munck[10]通过插值算法重构信号，移除旋转速度的影响达到使用阶次描述系统特征的目的。Renaudin等[11]运用瞬时角速度(Instantaneous Angular Speed, IAS)结合阶次跟踪算法，实现了滚动轴承不变转速工作状态下的故障诊断。但通常情况下，IAS从时域信号分析获取，并不能精确计算得到。

近年来，通过学者的研究，小波熵和EMD熵能够较好地描述设备的退化损伤状态[7]。同时阶次跟踪算法能够移除不同转速带来的影响，滚动轴承的特征频率(阶次)可以精确计算得到，提出了一个结合能量熵和阶次跟踪算法的滚动轴承损伤状态评估方法。首先运用互补总体平均经验模态分解(Complete Ensemble Empirical Mode Decomposition, CEEMD)将原始信号分解为一系列的固有模态函数(Intrinsic Mode Function, IMF)，选取其中包含大量滚动轴承特征信息的IMF分量。由于希尔伯特变换会得到没有物理意义的负频率，这里运用改进的希尔伯特变换计算IMF分量的瞬时频率和瞬时幅度，并得到这些IMF分量的边际谱。利用阶次跟踪算法得到阶次幅值图，选取各特征阶次幅值和能量熵作为特征参数，并采用遗传算法(Genetic Algorithm, GA)优化的支持向量机(Support Vector Machine，SVM)对滚动轴承的各损伤状态进行诊断识别。

1 CEEMD方法和经验归一化过程

经验模态分解(empirical mode decomposition，EMD)是一种适于非线性、非平稳信号的自适应信号处理方法。其本质是对非平稳信号进行平稳化处理，将信号中不同尺度的波动或趋势逐级分解出来。同时，EMD方法也存在一些不足如模态混叠现象，为了克服EMD的模态混叠问题，文献[12]提出了一种集合经验模态分解(ensemble EMD，EEMD)方法。EEMD利用白噪声具有频率均匀分布的统计特性，当信号加入高斯白噪声后，使信号在不同尺度上具有连续性，改变信号极值点的特性，促进抗混叠分解，有效地避免了模态混叠现象。但同时在信号中加入白噪声，使分解的结果带来了重构误差。为了克服噪声对分解结果的影响，文献[13]提出了CEEMD方法，能够在保证分解效果与EEMD相当的情况下，克服所添加的噪声对分解结果的影响。其分解步骤如下：

1)向待分解信号中加入n组正、负成对的辅助白噪声，从而生成2套集合IMF。

(1)

式中：S为原信号；N为辅助噪声；M1，M2分别为加入正负成对噪声后的信号。这样得到集合信号的个数为2n。

2)对集合中的每个信号进行EMD分解，每个信号得到1组IMF分量，其中第i个信号的第j个IMF分量用cij表示。

3)对多组IMF分量进行组合，得到分解结果如下：

(2)

其中cj即为CEEMD分解最终获得的第j个IMF分量。

1.2 CEEMD能量熵

为了得到CEEMD能量熵，首先将振动信号进行CEEMD分解，计算各个IMF分量的总能量，计算公式如下：

2.3.5 地瓜的收获：地瓜没有明显的成熟标准和收获期，一般都在10月中旬，初霜前收获，注意不要刨伤地瓜，小心运输，不要碰破皮，选出受伤的地瓜，以免影响贮存。

(3)

其中N为每个IMF分量的数据点数。

能量熵的计算方法为：

(4)

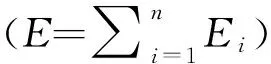
本文构建状态识别的特征向量T=[E1，E2，…，Em]，考虑到能量有时候数值非常大，这里对其进行归一化。

(5)

归一化后得到的特征向量为：

T′=[E1/S，E2/S，…，Em/S]。

(6)

1.3 经验归一化过程

将原始信号经过CEEMD分解后，各IMF分量cj(t)的Hilbert变换可表示为：

(7)

信号c(t)的解析信号z(t)可定义为：

z(t)=c(t)+iy(t)=A(t)eiθt。

(8)

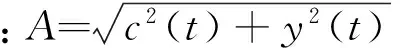
频率便可定义为相位θ(t)对时间t的求导：

(9)

运用3次样条曲线将IMF分量cj(t)的所有极大值点连接起来，便可得到IMF分量的经验包络e1(t)。 然后这个经验包络e1(t)被用来归一化该IMF分量c(t)：

(10)

利用y1(t)的经验包络e2(t)重复进行式(10)中的归一化过程：

(11)

当yn(t)的所有值都小于或者等于整体的时候，这个归一化过程就完成了。

定义yn(t)为IMF分量cj(t)的经验调幅部分：

yn(t)=cosφ(t)=F(t)。

(12)

式中F(t)为统一幅值下的纯调频函数，则调幅部分A(t)为：

(13)

根据式(4)，可以得到：

x(t)=A(t)×F(t)=A(t)cosφ(t)。

(14)

此时即完成了经验频率调制和幅度调制过程，可以发现，经验幅度调制较为平滑而且有效避免了高频波动和幅度调制系数过调。

计算频率，对相位函数微分：

(15)

振动信号的时间-频率-幅度谱可表示为：

(16)

则包含p个IMF分量信号的边际谱为：

(17)

2 应用分析

采用美国凯斯西储大学(CaseWesternReserveUniversity)电气工程实验室的滚动轴承试验数据对所提的方法进行验证[14]，实验装置如图1所示，左端是一个1.47kW的电机，中间连接部分安装了扭矩传感器，右侧是负载(电力测功机)和电子控制设备(图中没有显示)。运用加速度传感器采集了滚动轴承运行正常、外圈损伤、内圈损伤和滚珠损伤时的振动信号。

图1 轴承测试平台示意图Fig.1 Schematic diagram of bearing test platform

采用转速和载荷分别为1 730r/min和3HP，1 750r/min和2HP，1 772r/min和1HP，1 797r/min和0HP四种工况下，故障直径分别为0.18mm和0.54mm两种状态下的轴承振动信号对所提的方法进行验证。如表1所示，本次试验包括4种不同工况条件和7种轴承损伤状态，针对各个工作状态条件下的每个损伤状态采集20组数据，一共560组数据，(每种损伤状态80个，其中40个用来训练，40个用作测试)。

表1 试验中各状态编号Tab.1 Condition numbers in the experiment

试验中所采用的滚动轴承主要参数为，轴承直径39.04mm，滚珠直径7.94mm，滚珠数量为9个，则滚动轴承各故障状态下的特征阶次为：

(18)

式中：OR为轴频；OBPFO为外圈磨损状态；OBPFI为滚珠磨损状态；OBSF为内圈磨损状态。

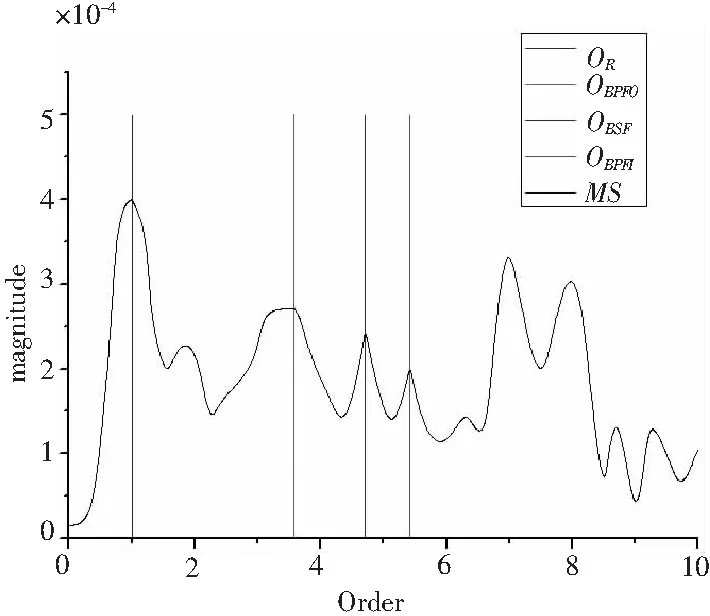
图2 轴承滚动体轻微损伤边际谱Fig.2 Marginal spectrum of bearing with slight rolling element defects

将振动信号进行CEEMD分解后，选取包含主要损伤特征的IMF分量，分别进行经验归一化求得频率调制和幅度调制，并计算得到这些IMF分量的时间-频率-幅度谱，进一步计算这些IMF分量组成的边际谱。而特征阶次可以较好地消除转速不同带来的影响。根据边际谱和特征阶次，得到各特征阶次对应的边际谱幅值。并且能量熵能够较好地表征各个损伤状态，由式(6)计算每组数据的CEEMD能量熵。最后结合特征阶次边际谱值和CEEMD能量熵构建滚动轴承损伤状态识别的特征向量。将训练和测试各280组特征向量进行归一化后，分别对遗传算法优化的支持向量机进行训练和测试，最终的诊断结果如表2所示。

根据表2的计算结果，状态2的损伤状态识别精度最高达到了100%，状态6的识别精度最低为85%，280组样本的平均准确率为93.21%。针对不同的工况条件，所提的多工况滚动轴承损伤状态识别方法有效。这是因为提取的故障特征中包含CEEMD熵和特征阶次幅值，CEEMD熵针对滚动轴承不同的故障及损伤状态识别效果较好，而各故障状态的特征阶次幅值能够消除转速的不同带来的影响。

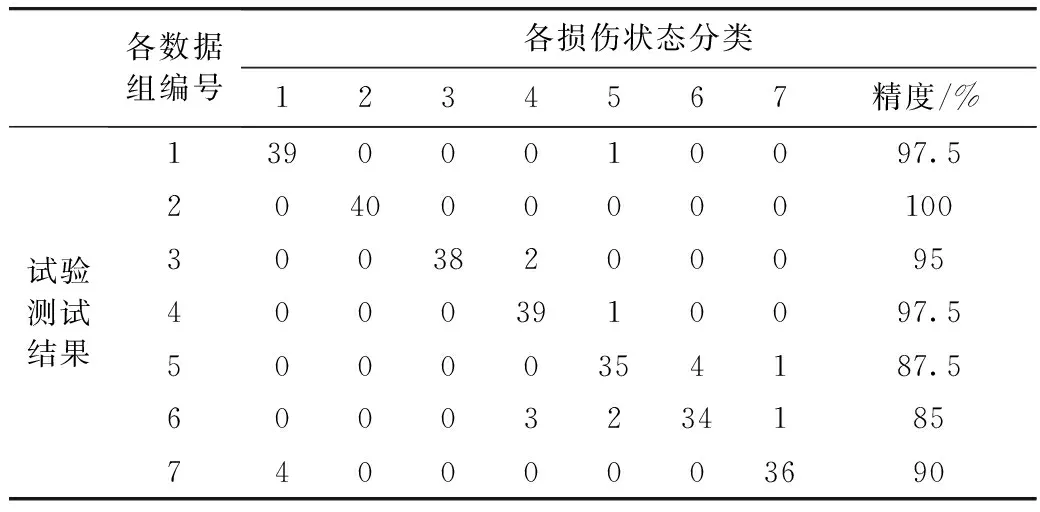
表2 各故障状态SVM识别结果Tab.2 SVM recognition results of the defect conditions

3 结 语

本文提出了一种基于CEEMD能量熵、边际谱阶次跟踪和支持向量机的滚动轴承损伤状态识别方法。通过CEEMD方法将原始信号分解为一系列的IMF分量，计算各IMF分量的能量熵，并采用经验归一化的希尔伯特变换计算各包含损伤特征的IMF分量的时间-频率-幅度谱和边际谱，结合边际谱中各特征阶次的幅值与能量熵构建特征向量，最后利用GA优化的SVM评估滚动轴承在多工况条件下的损伤状态。试验结果表明，针对多工况条件下的滚动轴承损伤状态评估，所提方法能够较好地识别滚动轴承各故障损伤状态，表明所提的方法有效。

[1]PAYABA,ESATII,BADIMNM.Artificialneuralnetworkbasedfaultdiagnosticsofrotatingmachineryusingwavelettransformsasapreprocessor[J].MechanicalSystemsandSignalProcessing，1997，11(5)：751-765.

[2]BATISTAL,BADRIB,SABOURINR,etal.Aclassifierfusionsystemforbearingfaultdiagnosis[J].ExpertSystemswithApplications,201340：6788-6797.

[3]GRYLLIASKC,I.A.Antoniadis.ASupportVectorMachineapproachbasedonphysicalmodeltrainingforrollingelementbearingfaultdetectioninindustrialenvironments[J].EngineeringApplicationsofArtificialIntelligence,2012，25：326-344.

[4]LIZX,YANXP,YUANCQ,etal.Faultdetectionanddiagnosisofagearboxinmarinepropulsionsystemsusingbispectrumanalysisandartificialneuralnetworks[J].JournalofMarineScienceandApplication，2011，10：17-24.

[5] 曾庆虎，邱静，刘冠军，等.基于小波相关滤波-包络分析的早期故障特征提取方法[J].仪器仪表学报，2008(4)：730-733.

ZENGQin-shu，QIUJing，LIUGuan-jun，etal.Approachtoextractionofincipientfaultfeaturesbasedonwaveletcorrelationfilterandenvelopeanalysis[J].ChineseJournalofScientificInstrument，2008(4)：730-733.

[6]LINing,ZHOURui,HUQing-hua,etal.Mechanicalfaultdiagnosisbasedonredundantsecondgenerationwaveletpackettransform,neighborhoodroughsetandsupportvectormachine[J].MechanicalSystemsandSignalProcessing,2012，28：608-621.

[7]YANGYu,YUDe-jie,CHENGJun-sheng.ArollerbearingfaultdiagnosismethodbasedonEMDenergyentropyandANN[J].JournalofSoundandVibration,2006，294：269-277.

[8]WANGYan-xue,HEZheng-jia,XIANGJia-wei,etal.Applicationoflocalmeandecompositiontothesurveillanceanddiagnosticsoflow-speedhelicalgearbox[J].MechanismandMachineTheory,2012，47：62-73.

[9]LOUGHLINPJ,TACERB.Instantaneousfrequencyandtheconditionalmeanfrequencyofasignal[J].SignalProcessing,1997，60：153-162.

[10]FYFEKR,MUNCKEDS.Analysisofcomputedordertracking[J].MechanicalSystemsandSignalProcessing,1997(11)：187-205.

[11]RENAUDINL,BONNARDOTF,MUSYO,etal.Naturalrollerbearingfaultdetectionbyangularmeasurementoftrueinstantaneousangularspeed[J].MechanicalSystemsandSignalProcessing,2010(24)：1998-2011.

[12]WUZ,HUANGNE.Ensembleempiricalmodedecompo-sition:Anoiseassisteddataanalysismethod[J].DataAnal，2009(1): 1-41.

[13]YEHJR,SHIEHJS.complementaryensembleempiricalmodedecomposition:anovelnoiseenhanceddataanalysismethod[J].AdvancesinAdaptiveDataAnalysis,2010,2(2):135-156.

[14]http://csegroups.case[EB/OL].edu/bearingdatacenter/pages/download-data-file.

A rolling bearing damage state recognition method under variable condition

ZHOU Tao-tao1,2，ZHU Xian-ming1,2，LIU Yan1,2，PENG Wei-cai1,2

(1.China Ship Development and Design Center,Wuhan 430064,China; 2.National Key Laboratory on Ship Vibration and Noise, China Ship Development and Design Center,Wuhan 430064,China)

Aim at bearing defect identification under varying operating conditions, a damage recognition method based on CEEMD energy entropy and order tracking method was proposed.The vibration signal was decomposed into a series of IMF components by CEEMD; the IMF components containing bearing defect characteristic frequency were selected; improved Hilbert transform was applied to compute the marginal spectrum from these IMF components; order tracking method was utilized to eliminate the effects of variable rotating speed; CEEMD energy entropy was used for damage state identification.Finally, the magnitudes of characteristic orders and CEEMD energy entropy were used to construct the diagnose feature vectors, and genetic algorithm optimized support vector machines was employed for damage state identification.The experimental results show that the method based on CEEMD energy entropy and order tracking is a promising and effective damage identification method with high accuracy.

fault defect identification; order-tracking; CEEMD energy entropy; SVM

2015-05-04；

2015-06-01

国家自然科学基金资助项目(51409238)

周涛涛(1988-)，男，博士研究生，研究方向为故障预测与健康管理。

TP18

A

1672-7649(2015)10-0067-05

10.3404/j.issn.1672-7649.2015.10.014