基于编织点起始位置及牵拉速度变化的编织角预测模型

王晓明，邹 婷，李超婧，王 璐

(1.东华大学纺织学院，上海 201620;2.东华大学纺织面料技术教育部重点实验室，上海 201620)

编织作为一种纺织品生产技术可追溯到18世纪［1］，现今编织结构已经不再局限在纺织领域的应用，采用编织技术制得的支架管［2］、缝合线［3］、神经导管［4－5］、人造血管［6］等已应用于医疗领域，制得的复合材料预成型体也已应用于航天、汽车工业［7］。典型的二维编织机上有2组携纱器，在相互交叉的蜿蜒轨道，一组携纱器沿着顺时针方向运动，另一组携纱器沿着逆时针方向运动，这就使得纱线产生交织，并最终形成编织结构［1］。

在二维编织机上编织管状织物时，一般采用带芯编织的方法，即在编织机的中心放1根芯棒，使纱线在芯棒上交织，芯棒的外径可根据所要编织的管状织物的内径来选择［4］。编织织物的一个优点就是织物中纤维束的取向角能够改变，这个取向角称之为编织角，即编织织物中纤维束与轴向的夹角［1］。因为编织织物的编织角会影响物理性能，例如织物的抗疲劳性［8］、拉伸强力［9］、刚度［10］、模量［11］等，而且编织角会影响编织织物的孔径大小以及织物的孔隙率［12］。

编织角作为编织织物的一个重要参数，研究者建立了一系列关于编织角的研究和预测模型。Pastore等［13］建立了二维编织静态模型，阐述了稳定编织情况下编织角与牵拉速度、携纱器角速度和芯棒外径之间的关系。Du等［14］建立了编织旋转曲面的几何模型，能够预测编织角、纱线体积分数及纱线表面覆盖系数，尤其此模型能够预测对应芯棒上各点的编织结构。Lian等［15］描述了一种能够在实际编织过程动态测量编织角的图像处理系统，这种系统被一系列的二维三向编织预成型体所证实。Yan［16］等建立了一种二维三向编织的微结构模型，通过分析弹性变形能预测织物的物理性能。Long等［17］建立了一般截面形状芯棒的编织模型，用来预测编织织物的“锁结”编织角。

以往的二维编织模型根据牵拉速度、携纱器角速度和芯棒外径来预测编织角的变化，这种方法可以预测编织点稳定时编织角的值，但是不能预测编织角不稳定阶段编织角随时间的变化过程以及编织角稳定所需时间和这段时间编织的织物长度。在二维编织过程中，起始编织点的位置会影响编织的稳定性(即编织角的稳定性)，如果起始编织点高度高于(低于)设计的编织角对应的编织点的高度，那么编织点会下降(上升)直到稳定在设计编织角对应的编织点位置，就会造成编织角一直增大(减小)直到稳定在所设计的编织角。在编织过程中，增大(减小)牵拉速度会使编织点上升(下降)，直到稳定在改变后卷绕速度对应的编织点处，从而导致编织角的下降(上升)，但是，这些编织点或编织角变化都不是瞬间完成的，都需要一定的时间缓冲，具有一定的滞后性。

本文通过数学建模的方法建立编织高度和编织角随时间变化的本构方程，并且精确预测编织角从不稳定状态到稳定状态所需的时间以及在此过程中编织的织物长度，并且后续的实验结果也验证了模型的有效性。此模型对工业自动化生产以及实验研究具有一定的指导意义，特别是对实验研究中编织较短的管状物尤为重要。因为若编织的较短管状物起始编织点位置与设计的编织点位置不同，则有可能造成整根管状物结构的不均匀。在实际工业化生产中，改变编织过程中的卷绕速度，实际编织角会逐渐向设计的编织角去变化，但编织角的变化相对于卷绕速度的变化会有一定的滞后性，可以通过此模型精确预测这一滞后性的时间以及这段时间编织的织物长度。

1 编织点静态稳定模型

依据二维编织原理，芯棒沿竖直方向移动，携纱器在轨道盘的圆周方向呈S形交叉运动，二者的运动使得纱线以一定的角度沉积在芯棒上形成编织织物(见图1)。编织角θ是指纱线与编织织物轴向的夹角，它是由牵拉速度V、携纱器角速度ω以及芯棒半径 r共同决定的［13］(见图2)，则

图1 二维编织原理示意图Fig.1 2－D braiding mechanism

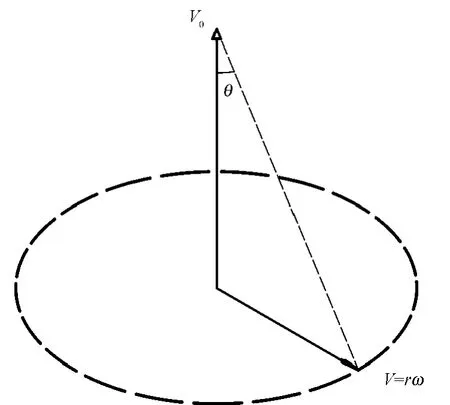
图2 编织角与速度向量示意图Fig.2 Braiding angle and velocity vector

在编织过程中，编织点的高度h指的是编织点至携纱器上导纱孔平面的垂直距离，编织机携纱器轨道的平均半径为R，某个编织高度h下对应的编织角即为编织纱与芯棒轴向的夹角(见图1)。则

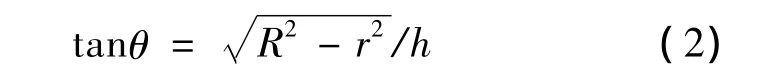
编织高度是一个因变量，随携纱器在轨道盘上运动的圆周速度(Vc=rω)与卷取速度(V)比值的变化而变化，当编织点稳定时，

2 编织点动态不稳定模型

立式编织机的牵拉速度V为竖直方向的，可分解为竖直方向上2个速度:一个是对未进行编织的纱线的牵拉速度(即编织点的运动速度VP)，另一个是对正在进行编织的纱线的牵拉速度VF。则

那么

当编织点稳定时，VP=0，V1=VF，则

若在编织过程中，牵拉速度由原来的V0变为V1，或起始编织点的高度h0与最终稳定时的编织点高度h1不相等时，编织点就会运动。当V0＜V1(或h0＜h1)时，编织点是上升的，是从编织点不稳定到稳定的过程中，VP、VF的变化如图3(a)所示;当V0＞V1(h0＞h1)时，编织点是下降的，是从编织点不稳定到稳定的过程中，VP、VF的变化如图3(b)所示。

3 编织角和编织点高度预测模型

3.1 起始编织点高度对编织角影响预测模型

若h0≠h1，当时间t=0时，即起始编织时(设起始编织角为θ0)，由式(2)可得:

对正在进行编织纱线的牵拉速度(VF0)，由式(5)可知:

在起始编织点处编织点的运动速度VP0，由式(4)可得:

对于起始编织点至稳定编织点之间的任一编织点，由式(2)、(5)可得:

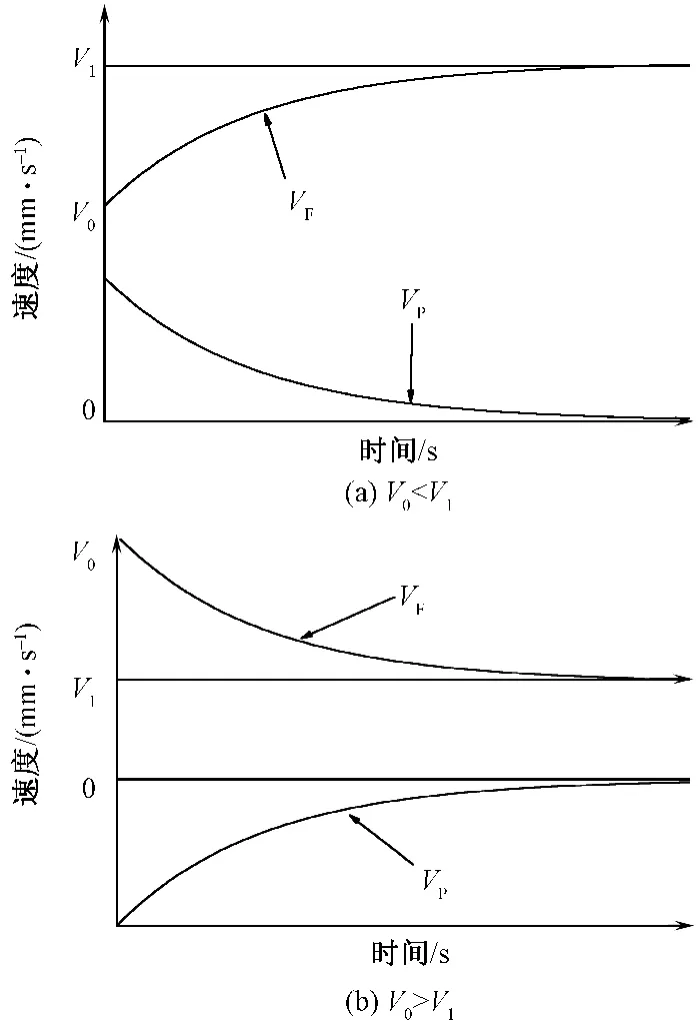
图3 VP与VF随时间变化曲线Fig.3 Change curve of VPand VFwith time

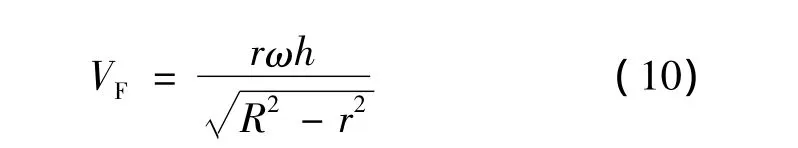
由式(4)、(10)可得:

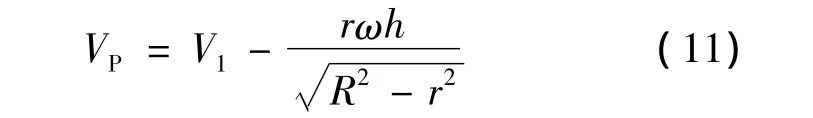
此点处在极短时间(△t)内，编织点走过的路程为△h，则

变为微分形式为

求解式(13)微分方程得:

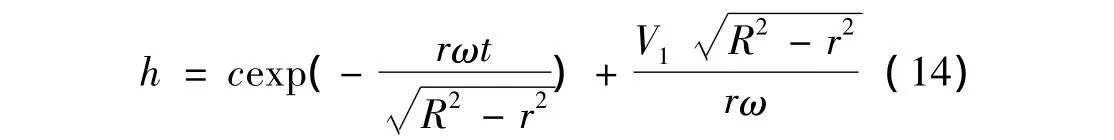
将t=0时，h=h0带入式(14)解得常数c，将常数c代入式(14)得:

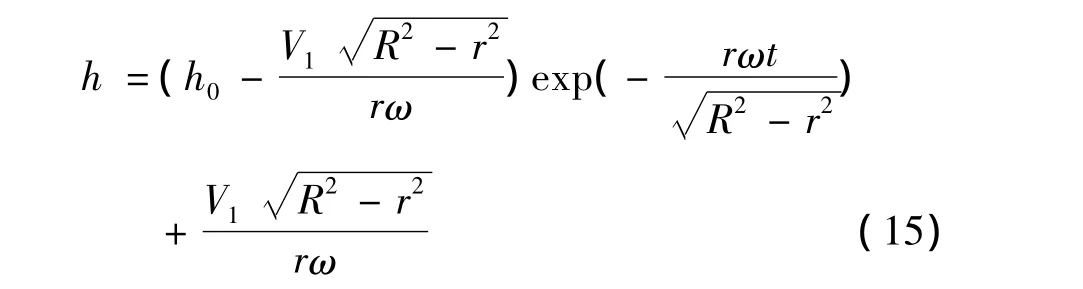
由式(2)、(15)可得:

对起始编织点和稳定编织点之间任意一个编织点的编织角θ，将式(15)与式(12)联立解得:

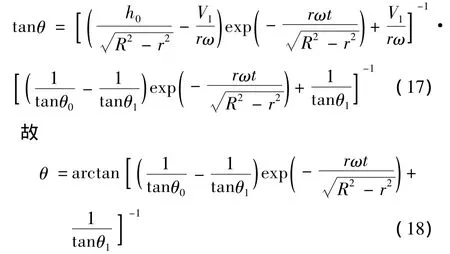
从数学角度，当t→+∝时，θ=θ1(θ1为编织稳定时的编织角)，但经过一段时间后编织角θ无限接近于θ1。从实际角度，当

就可认为编织点稳定，编织点从不稳定状态到稳定过程中所需的时间为T，由式(18)、(19)可得

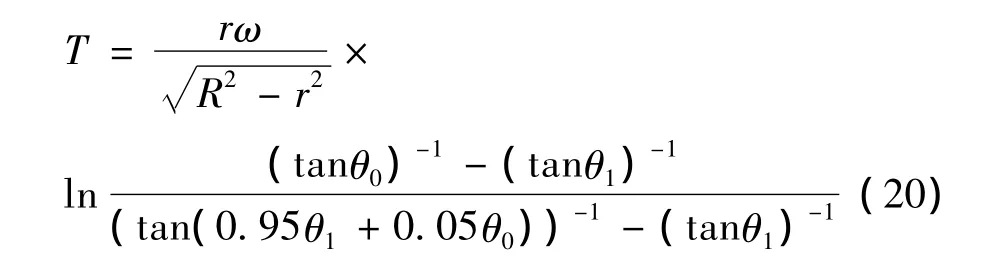
编织点从不稳定状态到稳定状态过程中，编织的管状物的长度为

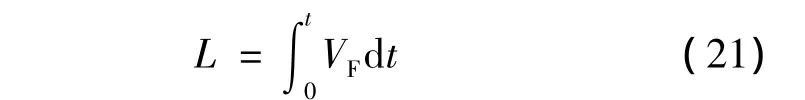
将式(10)、(16)与式(21)联立解得:

在编织点从不稳定到稳定状态下，总共编织的管状物的长度为LT，则

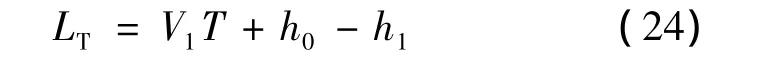
将式(20)代入式(23)可得:

3.2 牵拉速度对编织角影响预测模型

起始编织机的牵拉速度为V0，编织点高度稳定在h0处，而后改变编织机牵拉速度，使编织机牵拉速度突然变为V1，经过一段时间后编织点的高度稳定在h1，这个转化可用起始编织点高度对编织角影响预测模型表达，利用该预测模型能预测变换牵拉速度对编织角的影响。

4 模型的实验验证

为验证上述模型的有效性，采用带芯编织的方法，在外径为6mm的圆形聚四氟乙烯芯棒上进行编织。任意选择实验室现有的编织机，分别选择12锭和16锭编织机，编织机的轨道盘平均半径R分别为82mm和105mm，将实验结果与式(18)、(25)推出的理论结果进行了对比。

设计编织角是通过牵拉速度和携纱器圆周速度的速比来控制的。其中，携纱器的转速ω和芯棒外径r都是恒定的，分别为0.3 rad/s和6mm。设计编织角为 35°、50°、65°，编织机的实际牵拉速度分别为2.65、1.55、0.87mm/s。当轨道盘平均半径为82mm，起始编织角为 35°、50°、65°，对应的起始编织点高度分别为116.8、68.6、38.1mm;当轨道盘平均半径为 105mm，起始编织角为 35°、50°、65°，对应的起始编织点高度分别为149.8、87.9、48.9mm。实际编织角的测量是通过将织物在显微镜下拍照，再通过MB－ruler软件测量得到。

图4示出起始编织点高度对编织角影响随时间变化的实验数据以及由式(18)导出的理论曲线图。图4(a)、(b)为采用轨道盘平均半径为82mm、12锭编织机编织得到的结果;图4(c)、(d)示出采用轨道盘平均半径为105mm、16锭编织机编织得到的结果。表1示出编织从不稳定到稳定状态编织织物的长度的实验数据和由式(24)导出的理论数值，其中θ0为起始编织角，θ1为设计的编织角。

从图4和表1可以看出:模型预测结果与实验结果很吻合;编织角从不稳定到稳定状态，前期的编织角变化速度要明显快于后期;轨道盘的平均半径越大，编织角从不稳定到稳定状态所需的时间越久，这段时间编织的织物长度也越长;轨道盘半径相同，起始编织角与设计编织角的差值绝对值相同，设计牵拉速度V1越快，编织从不稳定状态到稳定状态编织的织物长度越长。从表1可看出，不稳定到稳定状态编织的实际织物长度与理论值存在一定偏差，这可能是由于实际编织过程纱线与机件摩擦以及实验测量误差导致的。

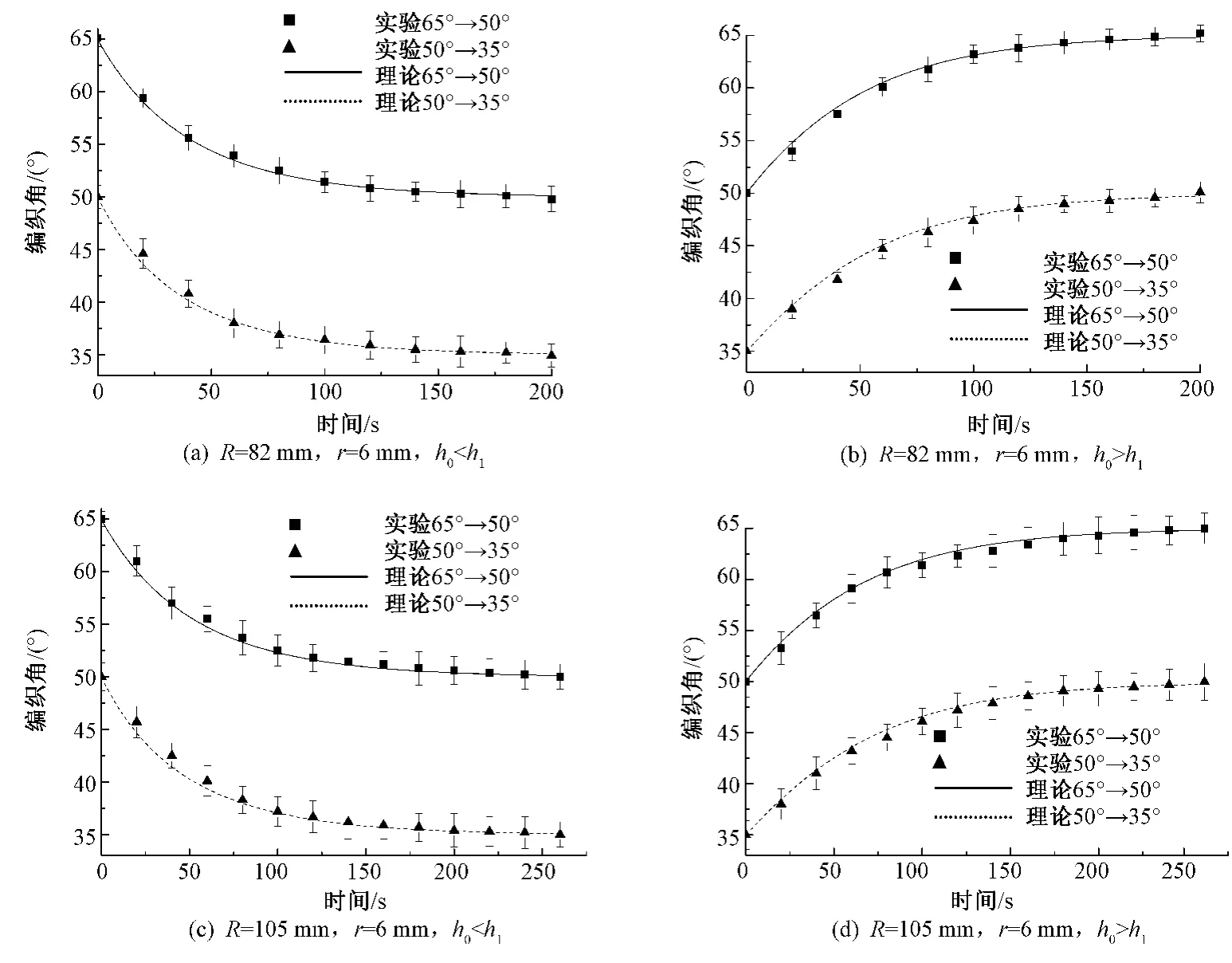
图4 编织角滞后图Fig.4 Hysteresis of braiding angle

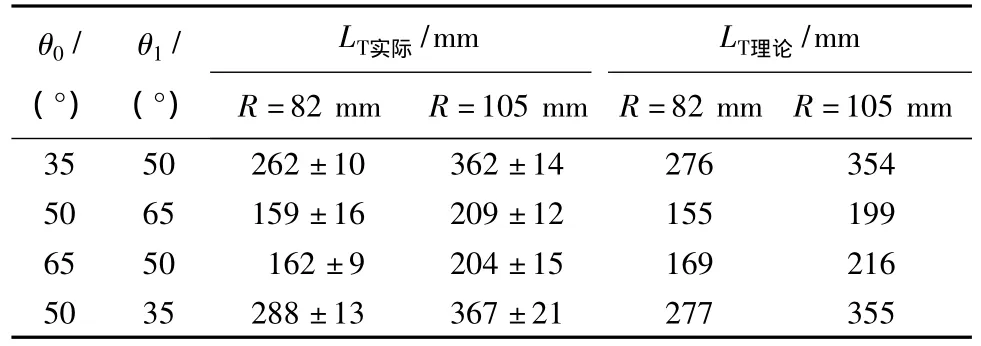
表1 从不稳定到稳定状态编织的织物长度Tab.1 Length of braiding fabric from unsteady to steady condition

起始编织点高度与设计的编织点高度不同，或改变编织机的卷绕速度，都会导致编织角的变化，但是这些变化都不是瞬时的。由式(18)、(25)可得:轨道盘平均半径越大，编织角从不稳定到稳定状态所需的时间越久，这段时间编织织物越长;芯棒外径越大，携纱器的转速越快，编织角从不稳定到稳定状态所需的时间越短。

5 结语

编织过程中，起始编织点高度与设计的编织点高度不同，或改变编织机的牵拉速度，都会导致编织点的不稳定，从而导致编织角的变化，但是这些变化都不是瞬时完成的。通过模型能够精确预测，编织点从不稳定状态到稳定状态过程中编织角随时间的变化、这个过程稳定所需时间以及编织织物的长度。本文建立了编织动态不稳定模型，为分析编织问题提供了一种方法。2009，15(3):387－402.

［1］AYRANCI C，CAREY J.2－D braided composites:a review for stiffness critical applications［J］.Composite Structures，2008，85(1):43－58.

［2］ZHANG M Q，ZOU T，HUANG Y C，et al.Braided thin－walled biodegradable ureteral stent:preliminary evaluation in a canine model［J］.International Journal of Urology，2014，21(4):401 －407.

［3］LO I K Y，BURKHART S S，ATHANASIOU K.Abrasion resistance oftwo types of nonabsorbable braided suture［J］.The Journal of Arthroscopic ＆Related Surgery，2004，20(4):407－413.

［4］刘国华.编织结构生物可降解神经再生导管的制造及性能研究［D］.上海:东华大学，2006:33－34.LIU Guohua.Fabrication and properties of braided biodegradable nerve regeneration conduits［D］.Shanghai:Donghua University，2006:33 －34.

［5］ICHIHARA S， INADA Y， NAKADA A， etal.Development of new nerve guide tube for repair of long nerve defects［J］.Tissue Engineering Part C:Methods，2009，15( 3) : 387－402.

［6］CAREY J，FAHIM A，MUNRO M.Design of braided composite cardiovascular catheters based on required axial，flexural，and torsional rigidities［J］.Journal of Biomedical Materials Research，Part B:Applied Biomaterials，2004，70(1):73－81.

［7］BRANSCOMB D，BEALE D，BROUGHTON R.New directions in braiding［J］. Journal of Engineered Fabrics＆ Fibers(JEFF)，2013，8(2):11－24.

［8］KELKAR A D，TATE J S，BOLICK R.Structural integrity of aerospace textile composites under fatigue loading［J］.Materials Science and Engineering:B，2006，132(1):79－84.

［9］SMITH L V，SWANSON S R.Strength design with 2－D triaxial braid textile composites［J］.Composites Science and Technology，1996，56(3):359－365.

［10］HUANG Z M，FUJIHARA K.Stiffness and strength design of composite bone plates［J］.Composites Science and Technology，2005，65(1):73－85.

［11］AYRANCI C，CAREY J P.Predicting the longitudinal elastic modulus of braided tubular composites using a curved unit－cell geometry［J］.Composites Part B:Engineering，2010，41(3):229－235.

［12］吕运转，陈南梁.编织型神经再生导管的孔隙率表征［J］.产业用纺织品，2009(2):38－41.LÜ Yunzhuan，CHEN Nanliang.The characterization of porosity with braided biodegradable nerve regeneration conduits［J］.Technical Textiles，2009(2):38 － 41.

［13］PASTORE C，KO F.CIM of braided preforms for compo－sites［C］//Proc.National Sampe Symposium and Exhibition.San Diego:［s.n.］，1998:133－155.

［14］DU G，POPPER P.Analysis of a circular braiding process for complex shapes［J］.Journal of the Textile Institute，1994，85(3):316－337.

［15］LIAN B，JIANG L，MCGRATH J J，et al.Quantitative determination of morphological features of triaxially braided composites by the use of machine vision［J］.Composites Science and Technology，2000，60(2):159－166.

［16］YAN Y，HOA S V.An energy approach for the prediction of effective stiffness of 2－D braided composites［C］//Proc 12th Int Conf on Composite Materials.Paris:［s.n.］，1999.

［17］LONG A C.Process modelling for liquid moulding of braided preforms［J］.Composites Part A:Applied Science and Manufacturing，2001，32(7):941－953.